Поток

Математическая концепция, применимая к физике

Поток описывает любой эффект, который, как кажется, проходит или перемещается (независимо от того, движется ли он на самом деле или нет) через поверхность или вещество. Поток — это концепция в прикладной математике и векторном исчислении , которая имеет множество приложений в физике . Для явлений переноса поток — это векторная величина, описывающая величину и направление потока вещества или свойства. В векторном исчислении поток — это скалярная величина, определяемая как поверхностный интеграл перпендикулярной составляющей векторного поля по поверхности. ^[1]

Терминология

Слово «flux» происходит от латинского : fluxus означает «течь», а fluere — «течь». ^[2] Как и флюксия , этот термин был введен в дифференциальное исчисление Исааком Ньютоном .

Концепция теплового потока была ключевым вкладом Жозефа Фурье в анализ явлений теплопередачи. ^[3] Его основополагающий трактат Théorie analytique de la chaleur ( Аналитическая теория тепла ) ^[4] определяет поток как центральную величину и переходит к выводу ныне известных выражений потока в терминах разности температур по всей пластине, а затем в более общем смысле в терминах градиентов температуры или дифференциалов температуры по другим геометриям. Можно утверждать, основываясь на работе Джеймса Клерка Максвелла ^[5] , что определение переноса предшествует определению потока, используемого в электромагнетизме . Конкретная цитата из Максвелла:

В случае потоков мы должны взять интеграл по поверхности от потока через каждый элемент поверхности. Результат этой операции называется поверхностным интегралом потока. Он представляет собой количество, которое проходит через поверхность.

—  Джеймс Клерк Максвелл

Согласно определению переноса, поток может быть одним вектором или векторным полем / функцией положения. В последнем случае поток можно легко проинтегрировать по поверхности. Напротив, согласно определению электромагнетизма, поток является интегралом по поверхности; нет смысла интегрировать поток второго определения, поскольку это было бы интегрированием по поверхности дважды. Таким образом, цитата Максвелла имеет смысл только в том случае, если «поток» используется согласно определению переноса (и, кроме того, является векторным полем, а не одним вектором). Это иронично, потому что Максвелл был одним из главных разработчиков того, что мы теперь называем «электрическим потоком» и «магнитным потоком» согласно определению электромагнетизма. Их названия в соответствии с цитатой (и определением переноса) были бы «поверхностный интеграл электрического потока» и «поверхностный интеграл магнитного потока», и в этом случае «электрический поток» вместо этого определялся бы как «электрическое поле», а «магнитный поток» определялся бы как «магнитное поле». Это подразумевает, что Максвелл рассматривал эти поля как потоки/течения определенного рода.

Учитывая поток согласно определению электромагнетизма, соответствующая плотность потока , если этот термин используется, относится к его производной вдоль поверхности, которая была интегрирована. Согласно Фундаментальной теореме исчисления , соответствующая плотность потока является потоком согласно определению переноса. Учитывая ток, такой как электрический ток — заряд за время, плотность тока также будет потоком согласно определению переноса — заряд за время на площадь. Из-за противоречивых определений потока и взаимозаменяемости потока , потока и тока в нетехническом английском языке все термины, используемые в этом абзаце, иногда используются взаимозаменяемо и неоднозначно. Конкретные потоки в остальной части этой статьи будут использоваться в соответствии с их широким признанием в литературе, независимо от того, какому определению потока соответствует термин.

Поток как скорость потока на единицу площади

В явлениях переноса ( теплопередача , массопередача и гидродинамика ) поток определяется как скорость потока свойства на единицу площади, которая имеет размерность [количество]·[время] ⁻¹ ·[площадь] ⁻¹ . ^[6] Площадь — это часть поверхности, через которую свойство течет «через» или «через». Например, количество воды, протекающее через поперечное сечение реки каждую секунду, деленное на площадь этого поперечного сечения, или количество солнечной энергии, попадающее на участок земли каждую секунду, деленное на площадь участка, являются видами потока.

Общее математическое определение (транспорт)

Линии поля векторного поля F через поверхности с единичной нормалью n , угол от n до F равен θ . Поток является мерой того, какая часть поля проходит через данную поверхность. F разлагается на компоненты, перпендикулярные (⊥) и параллельные ( ‖ ) n . Только параллельная компонента вносит вклад в поток, поскольку она представляет собой максимальную протяженность поля, проходящего через поверхность в точке, перпендикулярная компонента не вносит вклада. Вверху
: три линии поля через плоскую поверхность, одна нормальная к поверхности, одна параллельная и одна промежуточная.
Внизу: линия поля через криволинейную поверхность , показывающая настройку единичной нормали и элемента поверхности для расчета потока.

Для вычисления потока векторного поля F (красные стрелки) через поверхность S поверхность делится на небольшие участки dS . Поток через каждый участок равен нормальной (перпендикулярной) составляющей поля, скалярному произведению F ( x ) с единичным нормальным вектором n ( x ) (синие стрелки) в точке x, умноженному на площадь dS . Сумма F · n , dS для каждого участка на поверхности является потоком через поверхность

Вот 3 определения в порядке возрастания сложности. Каждое из них является частным случаем следующего. Во всех случаях частый символ j (или J ) ​​используется для потока, q для физической величины, которая течет, t для времени и A для площади. Эти идентификаторы будут написаны жирным шрифтом тогда и только тогда, когда они являются векторами.

Во-первых, поток как (единичный) скаляр: где В этом случае поверхность, на которой измеряется поток, фиксирована и имеет площадь A. Поверхность предполагается плоской, а поток предполагается всюду постоянным относительно положения и перпендикулярным поверхности. $${\displaystyle j={\frac {I}{A}},}$$ $${\displaystyle I=\lim _{\Delta t\to 0}{\frac {\Delta q}{\Delta t}}={\frac {\mathrm {d} q}{\mathrm {d} t}}.}$$

Во-вторых, поток как скалярное поле , определенное вдоль поверхности, т. е. функция точек на поверхности: Как и прежде, поверхность предполагается плоской, а поток предполагается всюду перпендикулярным ей. Однако поток не обязательно должен быть постоянным. q теперь является функцией p , точки на поверхности, и A , площади. Вместо того, чтобы измерять полный поток через поверхность, q измеряет поток через диск с площадью A, центрированной в p вдоль поверхности. $${\displaystyle j(\mathbf {p} )={\frac {\partial I}{\partial A}}(\mathbf {p} ),}$$ $${\displaystyle I(A,\mathbf {p} )={\frac {\mathrm {d} q}{\mathrm {d} t}}(A,\mathbf {p} ).}$$

Наконец, поток как векторное поле : в этом случае нет фиксированной поверхности, над которой мы проводим измерения. q является функцией точки, площади и направления (заданного единичным вектором ) и измеряет поток через диск площадью A, перпендикулярный этому единичному вектору. I определяется выбором единичного вектора, который максимизирует поток вокруг точки, поскольку истинный поток максимизируется через диск, который перпендикулярен ему. Таким образом, единичный вектор однозначно максимизирует функцию, когда он указывает в «истинном направлении» потока. (Строго говоря, это злоупотребление обозначениями , поскольку «arg max» не может напрямую сравнивать векторы; вместо этого мы берем вектор с наибольшей нормой.) $${\displaystyle \mathbf {j} (\mathbf {p} )={\frac {\partial \mathbf {I} }{\partial A}}(\mathbf {p} ),}$$ $${\displaystyle \mathbf {I} (A,\mathbf {p} )={\underset {\mathbf {\hat {n}} }{\operatorname {arg\,max} }}\mathbf {\hat {n}} _{\mathbf {p} }{\frac {\mathrm {d} q}{\mathrm {d} t}}(A,\mathbf {p} ,\mathbf {\hat {n}} ).}$$ ${\displaystyle \mathbf {\hat {n}} }$

Характеристики

Эти прямые определения, особенно последнее, довольно громоздки. Например, конструкция arg max является искусственной с точки зрения эмпирических измерений, когда с помощью флюгера или чего-то подобного можно легко вывести направление потока в точке. Вместо того чтобы определять векторный поток напрямую, часто более интуитивно понятно указать некоторые его свойства. Более того, из этих свойств поток в любом случае можно однозначно определить.

Если поток j проходит через область под углом θ к нормали области , то скалярное произведение То есть, компонент потока, проходящий через поверхность (т.е. нормальный к ней), равен j  cos  θ , тогда как компонент потока, проходящий по касательной к области, равен j  sin  θ , но фактически поток, проходящий через область в тангенциальном направлении, отсутствует . Единственным компонентом потока, проходящим по нормали к области, является косинусная компонента. ${\displaystyle \mathbf {\hat {n}} }$ $${\displaystyle \mathbf {j} \cdot \mathbf {\hat {n}} =j\cos \theta .}$$

Для векторного потока поверхностный интеграл j по поверхности S дает надлежащий поток в единицу времени через поверхность: где A (и его бесконечно малая величина) — это векторная площадь  — комбинация величины площади A , через которую проходит свойство, и единичного вектора, нормального к площади. В отличие от второго набора уравнений, поверхность здесь не обязательно должна быть плоской. $${\displaystyle {\frac {\mathrm {d} q}{\mathrm {d} t}}=\iint _{S}\mathbf {j} \cdot \mathbf {\hat {n}} \,dA=\iint _{S}\mathbf {j} \cdot d\mathbf {A} ,}$$ ${\displaystyle \mathbf {A} =A\mathbf {\hat {n}} }$ ${\displaystyle \mathbf {\hat {n}} }$

Наконец, мы можем снова проинтегрировать по промежутку времени от t ₁ до t ₂ , получив общее количество вещества, протекающего через поверхность за это время ( t ₂  −  t ₁ ): $${\displaystyle q=\int _{t_{1}}^{t_{2}}\iint _{S}\mathbf {j} \cdot d\mathbf {A} \,dt.}$$

Транспортные потоки

Восемь наиболее распространенных форм потоков, описанных в литературе по явлениям переноса, определяются следующим образом:

1. Поток импульса , скорость передачи импульса через единицу площади (Н·с·м ⁻² ·с ⁻¹ ). ( Закон вязкости Ньютона ) ^[7]
2. Тепловой поток , скорость теплового потока через единицу площади (Дж·м ⁻² ·с ⁻¹ ). ( Закон теплопроводности Фурье ) ^[8] (Это определение теплового потока соответствует первоначальному определению Максвелла.) ^[5]
3. Диффузионный поток , скорость движения молекул через единицу площади (моль·м ⁻² ·с ⁻¹ ). ( Закон диффузии Фика ) ^[7]
4. Объемный поток , скорость объемного потока через единицу площади (м ³ ·м ⁻² ·с ⁻¹ ). ( Закон Дарси о потоке грунтовых вод )
5. Поток массы , скорость потока массы через единицу площади (кг·м ⁻² ·с ⁻¹ ). (Либо альтернативная форма закона Фика, включающая молекулярную массу, либо альтернативная форма закона Дарси, включающая плотность.)
6. Поток излучения , количество энергии, передаваемой в виде фотонов на определенном расстоянии от источника на единицу площади в секунду (Дж·м ⁻² ·с ⁻¹ ). Используется в астрономии для определения звездной величины и спектрального класса звезды. Также выступает в качестве обобщения теплового потока, который равен потоку излучения, если ограничиться электромагнитным спектром.
7. Поток энергии , скорость передачи энергии через единицу площади (Дж·м ⁻² ·с ⁻¹ ). Лучистый поток и тепловой поток являются частными случаями потока энергии.
8. Поток частиц, скорость переноса частиц через единицу площади ([число частиц] м ⁻² ·с ⁻¹ )

Эти потоки являются векторами в каждой точке пространства и имеют определенную величину и направление. Также можно взять дивергенцию любого из этих потоков, чтобы определить скорость накопления количества в контрольном объеме вокруг заданной точки пространства. Для несжимаемого потока дивергенция объемного потока равна нулю.

Химическая диффузия

Как упоминалось выше, химический молярный поток компонента A в изотермической , изобарической системе определяется в законе диффузии Фика следующим образом: где символ набла ∇ обозначает оператор градиента , D _AB — коэффициент диффузии (м ² · с ⁻¹ ) компонента A, диффундирующего через компонент B, c _A — концентрация ( моль /м ³ ) компонента A. ^[9] $${\displaystyle \mathbf {J} _{A}=-D_{AB}\nabla c_{A}}$$

Этот поток имеет единицы моль·м ⁻² ·с ⁻¹ и соответствует первоначальному определению потока Максвелла. ^[5]

Для разбавленных газов кинетическая молекулярная теория связывает коэффициент диффузии D с плотностью частиц n = N / V , молекулярной массой m , сечением столкновения и абсолютной температурой T по формуле, где второй множитель — это длина свободного пробега , а квадратный корень (с постоянной Больцмана k ) — это средняя скорость частиц. ${\displaystyle \sigma }$ $${\displaystyle D={\frac {2}{3n\sigma }}{\sqrt {\frac {kT}{\pi m}}}}$$

В турбулентных потоках перенос вихревым движением может быть выражен как значительно увеличенный коэффициент диффузии.

Квантовая механика

В квантовой механике частицы массой m в квантовом состоянии ψ ( r , t ) имеют плотность вероятности, определяемую как Таким образом, вероятность обнаружения частицы в дифференциальном элементе объема d ³ r равна Тогда число частиц, проходящих перпендикулярно через единицу площади поперечного сечения за единицу времени, является потоком вероятности; Иногда это называют током вероятности или плотностью тока ^[10] или плотностью потока вероятности. ^[11] $${\displaystyle \rho =\psi ^{*}\psi =|\psi |^{2}.}$$ $${\displaystyle dP=|\psi |^{2}\,d^{3}\mathbf {r} .}$$ $${\displaystyle \mathbf {J} ={\frac {i\hbar }{2m}}\left(\psi \nabla \psi ^{*}-\psi ^{*}\nabla \psi \right).}$$

Поток как поверхностный интеграл

Общее математическое определение (поверхностный интеграл)

Визуализированный поток. Кольца показывают границы поверхности. Красные стрелки обозначают поток зарядов, частиц жидкости, субатомных частиц, фотонов и т. д. Количество стрелок, проходящих через каждое кольцо, — это поток.

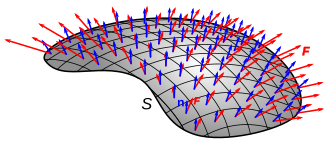
Как математическое понятие, поток представлен поверхностным интегралом векторного поля , ^[12]

${\displaystyle \Phi _{F}=\iint _{A}\mathbf {F} \cdot \mathrm {d} \mathbf {A} }$

${\displaystyle \Phi _{F}=\iint _{A}\mathbf {F} \cdot \mathbf {n} \,\mathrm {d} A}$

где F — векторное поле , а d A — векторная площадь поверхности A , направленная как нормаль к поверхности . Для второго n — единичный нормальный вектор, направленный наружу к поверхности.

Поверхность должна быть ориентируемой , т. е. можно различить две стороны: поверхность не загибается сама на себя. Кроме того, поверхность должна быть фактически ориентированной, т. е. мы используем соглашение о том, в каком направлении поток считается положительным; в таком случае поток назад считается отрицательным.

Нормаль к поверхности обычно направлена ​​по правилу правой руки .

Наоборот, можно считать поток более фундаментальной величиной и назвать векторное поле плотностью потока.

Часто векторное поле рисуется кривыми (линиями поля), следующими за "потоком"; величина векторного поля тогда является плотностью линий, а поток через поверхность - числом линий. Линии берут начало в областях положительной дивергенции (источники) и заканчиваются в областях отрицательной дивергенции (стоки).

См. также изображение справа: количество красных стрелок, проходящих через единицу площади, представляет собой плотность потока, кривая, окружающая красные стрелки, обозначает границу поверхности, а ориентация стрелок относительно поверхности обозначает знак внутреннего произведения векторного поля на нормали поверхности.

Если поверхность охватывает трехмерную область, то обычно поверхность ориентирована таким образом, что приток считается положительным; противоположным является отток .

Теорема о дивергенции утверждает, что чистый отток через замкнутую поверхность, другими словами, чистый отток из трехмерной области, находится путем сложения локального чистого оттока из каждой точки области (который выражается дивергенцией ) .

Если поверхность не замкнута, то она имеет ориентированную кривую в качестве границы. Теорема Стокса утверждает, что поток ротора векторного поля является линейным интегралом векторного поля по этой границе. Этот интеграл по траектории также называется циркуляцией , особенно в динамике жидкости. Таким образом, ротор является плотностью циркуляции.

Мы можем применить поток и эти теоремы ко многим дисциплинам, в которых мы видим токи, силы и т. д., приложенные через области.

Электромагнетизм

Электрический поток

Электрический «заряд», такой как одиночный протон в пространстве, имеет величину, определяемую в кулонах. Такой заряд имеет электрическое поле, окружающее его. В графической форме электрическое поле от положительного точечного заряда можно визуализировать как точку, излучающую линии электрического поля (иногда также называемые «силовыми линиями»). Концептуально электрический поток можно рассматривать как «количество линий поля», проходящих через заданную область. Математически электрический поток является интегралом нормальной составляющей электрического поля по заданной области. Следовательно, единицами электрического потока в системе MKS являются ньютоны на кулон , умноженные на квадратные метры, или Н м ² /Кл. (Плотность электрического потока является электрическим потоком на единицу площади и является мерой напряженности нормальной составляющей электрического поля, усредненной по области интегрирования. Ее единицами являются Н/Кл, то же самое, что и электрическое поле в единицах MKS.)

Используются две формы электрического потока , одна для электрического поля: ^{[13] [14]}

${\displaystyle \Phi _{E}=}$ ${\displaystyle {\scriptstyle A}}$ ${\displaystyle \mathbf {E} \cdot {\rm {d}}\mathbf {A} }$

и один для D -поля (называемого электрическим смещением ):

${\displaystyle \Phi _{D}=}$ ${\displaystyle {\scriptstyle A}}$ ${\displaystyle \mathbf {D} \cdot {\rm {d}}\mathbf {A} }$

Эта величина возникает в законе Гаусса , который гласит, что поток электрического поля E из замкнутой поверхности пропорционален электрическому заряду Q _A, заключенному в поверхности (независимо от того, как распределен этот заряд), интегральная форма имеет вид:

${\displaystyle {\scriptstyle A}}$ ${\displaystyle \mathbf {E} \cdot {\rm {d}}\mathbf {A} ={\frac {Q_{A}}{\varepsilon _{0}}}}$

где ε ₀ — диэлектрическая проницаемость свободного пространства .

Если рассмотреть поток вектора электрического поля, E , для трубки вблизи точечного заряда в поле заряда, но не содержащей его со сторонами, образованными линиями, касательными к полю, поток для сторон равен нулю, а на обоих концах трубки существует равный и противоположный поток. Это следствие закона Гаусса, примененного к обратному квадрату поля. Поток для любой поверхности поперечного сечения трубки будет тем же самым. Полный поток для любой поверхности, окружающей заряд q, равен q / ε ₀ . ^[15]

В свободном пространстве электрическое смещение задается конститутивным соотношением D = ε ₀ E , поэтому для любой ограничивающей поверхности поток поля D равен заряду Q _A внутри нее. Здесь выражение «поток» указывает на математическую операцию и, как можно видеть, результатом не обязательно является «поток», поскольку на самом деле ничто не течет вдоль линий электрического поля.

Магнитный поток

Плотность магнитного потока ( магнитное поле ), имеющая единицу измерения Вб/м ² ( Тесла ), обозначается буквой B , а магнитный поток определяется аналогично: ^{[13] [14]}

${\displaystyle \Phi _{B}=\iint _{A}\mathbf {B} \cdot \mathrm {d} \mathbf {A} }$

с теми же обозначениями, что и выше. Величина возникает в законе индукции Фарадея , где магнитный поток зависит от времени, либо потому, что граница зависит от времени, либо потому, что магнитное поле зависит от времени. В интегральной форме:

${\displaystyle -{\frac {{\rm {d}}\Phi _{B}}{{\rm {d}}t}}=\oint _{\partial A}\mathbf {E} \cdot d{\boldsymbol {\ell }}}$

где d ℓ — бесконечно малый векторный линейный элемент замкнутой кривой , величина которого равна длине бесконечно малого линейного элемента, а направление задается касательной к кривой , а знак определяется направлением интегрирования. ${\displaystyle \partial A}$ ${\displaystyle \partial A}$

Скорость изменения магнитного потока через петлю провода равна минус электродвижущая сила, создаваемая в этом проводе. Направление таково, что если ток проходит через провод, электродвижущая сила вызовет ток, который «противостоит» изменению магнитного поля, создавая магнитное поле, противоположное изменению. Это основа для индукторов и многих электрических генераторов .

Пойнтинга поток

Используя это определение, поток вектора Пойнтинга S по указанной поверхности представляет собой скорость, с которой электромагнитная энергия течет через эту поверхность, определяемую, как и ранее: ^[14]

${\displaystyle \Phi _{S}=}$ ${\displaystyle {\scriptstyle A}}$ ${\displaystyle \mathbf {S} \cdot {\rm {d}}\mathbf {A} }$

Поток вектора Пойнтинга через поверхность — это электромагнитная мощность , или энергия в единицу времени , проходящая через эту поверхность. Это обычно используется при анализе электромагнитного излучения , но применимо и к другим электромагнитным системам.

По непонятной причине вектор Пойнтинга иногда называют потоком мощности , что является примером первого использования потока выше. ^[16] Он имеет единицы измерения ватт на квадратный метр (Вт/м ² ).

Единицы радиометрии СИ

1. Организации по стандартизации рекомендуют обозначать радиометрические величины суффиксом «e» (от «энергетический»), чтобы избежать путаницы с фотометрическими или фотонными величинами.
2. Иногда встречаются альтернативные символы: W или E для лучистой энергии, P или F для лучистого потока, I для облученности, W для лучистой светимости.
3. Спектральные величины, заданные на единицу частоты , обозначаются суффиксом « ν » (греческая буква nu , не путать с буквой «v», обозначающей фотометрическую величину).
4. Спектральные величины, приведенные к единице длины волны, обозначаются суффиксом « λ ».
5. Направленные величины обозначаются суффиксом « Ω ».

Смотрите также

• Математический портал

• величина АВ
• Генератор компрессионного потока с взрывной накачкой
• Вихревой ковариационный поток (он же вихревая корреляция, вихревой поток)
• Испытательная установка Fast Flux
• Флюенс (поток первого рода для пучков частиц)
• Динамика жидкости
• След потока
• Закрепление потока
• Квантование потока
• Закон Гаусса
• Закон обратных квадратов
• Янский (внесистемная единица измерения спектральной плотности потока)
• Скрытый тепловой поток
• Световой поток
• Магнитный поток
• Квант магнитного потока
• Поток нейтронов
• Пойнтинга поток
• Теорема Пойнтинга
• Лучистый поток
• Быстрый однопоточный квант
• Поток звуковой энергии
• Объемный поток (поток первого рода для жидкостей)
• Объемный расход (поток второго рода для жидкостей)

Примечания

1. Перселл, стр. 22-26
2. Уикли, Эрнест (1967). Этимологический словарь современного английского языка . Courier Dover Publications. стр. 581. ISBN 0-486-21873-2.
3. Херивел, Джон (1975). Жозеф Фурье: человек и физик . Оксфорд: Clarendon Press. С. 181–191. ISBN 0-19-858149-1.
4. Фурье, Жозеф (1822). Théorie Analytique de la Chaleur (на французском языке). Париж: Firmin Didot Père et Fils. ОСЛК  2688081.
5. Максвелл, Джеймс Клерк (1892). Трактат об электричестве и магнетизме . ISBN 0-486-60636-8.
6. Берд, Р. Байрон ; Стюарт, Уоррен Э.; Лайтфут, Эдвин Н. (1960). Явления переноса . Wiley. ISBN 0-471-07392-X.
7. PM Whelan; MJ Hodgeson (1978). Essential Principles of Physics (2-е изд.). Джон Мюррей. ISBN 0-7195-3382-1.
8. Carslaw, HS; Jaeger, JC (1959). Теплопроводность в твердых телах (второе издание). Oxford University Press. ISBN 0-19-853303-9.
9. Уэлти; Уикс, Уилсон и Роррер (2001). Основы переноса импульса, тепла и массы (4-е изд.). Wiley. ISBN 0-471-38149-7.
10. D. McMahon (2008). Квантовая механика Демистифицирована (2-е изд.). Mc Graw Hill. ISBN 978-0-07-145546-6.
11. Сакурай, Дж. Дж. (1967). Advanced Quantum Mechanics . Addison Wesley. ISBN 0-201-06710-2.
12. Мюррей Р. Шпигель; С. Липшуц; Д. Спеллман (2009). Векторный анализ. Очерки Шаума (2-е изд.). McGraw Hill. стр. 100. ISBN 978-0-07-161545-7.
13. IS Grant; WR Phillips (2008). Электромагнетизм . Manchester Physics (2-е изд.). John Wiley & Sons . ISBN 978-0-471-92712-9.
14. DJ Griffiths (2007). Введение в электродинамику (3-е изд.). Pearson Education, Dorling Kindersley . ISBN 978-81-7758-293-2.
15. Лекции Фейнмана по физике, том II, гл. 4: Электростатика
16. Вангснесс, Роальд К. (1986). Электромагнитные поля (2-е изд.). Wiley. ISBN 0-471-81186-6.стр.357

• Браун, Майкл (2010). Физика для инженерии и науки, 2-е издание . Schaum Outlines. Нью-Йорк, Торонто: McGraw-Hill Publishing . ISBN 978-0-0716-1399-6.
• Перселл, Эдвард (2013). Электричество и магнетизм, 3-е издание . Кембридж, Великобритания: Cambridge University Press . ISBN 978110-7014022.

Дальнейшее чтение

• Stauffer, PH (2006). «Flux Flummoxed: A Proposal for Consistent Usage». Ground Water . 44 (2): 125–128. Bibcode : 2006GrWat..44..125S. doi : 10.1111/j.1745-6584.2006.00197.x . PMID  16556188. S2CID  21812226.

Внешние ссылки

• Словарное определение термина flux в Викисловаре