Аффинная связь

В дифференциальной геометрии аффинная связность ^[a] — это геометрический объект на гладком многообразии , который соединяет соседние касательные пространства , так что это позволяет дифференцировать касательные векторные поля , как если бы они были функциями на многообразии со значениями в фиксированном векторном пространстве . Связности являются одними из простейших методов определения дифференциации сечений векторных расслоений . [ ^3]

Понятие аффинной связности берет свое начало в геометрии и тензорном исчислении 19 века , но не было полностью разработано до начала 1920-х годов Эли Картаном (как часть его общей теории связностей ) и Германом Вейлем (который использовал это понятие как часть своих основ общей теории относительности ). Терминология принадлежит Картану ^[b] и берет свое начало в идентификации касательных пространств в евклидовом пространстве $R n$ путем перевода: идея состоит в том, что выбор аффинной связности делает многообразие бесконечно похожим на евклидово пространство не просто гладко, но и как аффинное пространство .

На любом многообразии положительной размерности существует бесконечно много аффинных связностей. Если многообразие дополнительно снабжено метрическим тензором , то существует естественный выбор аффинной связности, называемой связностью Леви-Чивиты . Выбор аффинной связности эквивалентен предписанию способа дифференцирования векторных полей, который удовлетворяет нескольким разумным свойствам ( линейность и правило Лейбница ). Это дает возможное определение аффинной связности как ковариантной производной или (линейной) связности на касательном расслоении . Выбор аффинной связности также эквивалентен понятию параллельного переноса , которое является методом переноса касательных векторов вдоль кривых. Это также определяет параллельный перенос на расслоении фреймов . Бесконечно малый параллельный перенос в расслоении фреймов дает другое описание аффинной связности, либо как связности Картана для аффинной группы , либо как главной связности на расслоении фреймов.

Главными инвариантами аффинной связности являются ее кручение и ее кривизна . Кручение измеряет, насколько точно скобка Ли векторных полей может быть восстановлена из аффинной связности. Аффинные связности также могут использоваться для определения (аффинных) геодезических на многообразии, обобщая прямые линии евклидова пространства, хотя геометрия этих прямых может сильно отличаться от обычной евклидовой геометрии ; основные различия заключены в кривизне связности.

Мотивация и история

Гладкое многообразие — это математический объект, который локально выглядит как гладкая деформация евклидова пространства $R n$ : например, гладкая кривая или поверхность локально выглядит как гладкая деформация линии или плоскости. Гладкие функции и векторные поля могут быть определены на многообразиях, так же как и на евклидовом пространстве, а скалярные функции на многообразиях могут быть дифференцированы естественным образом. Однако дифференциация векторных полей менее проста: в евклидовом пространстве это простой вопрос, потому что касательное пространство базовых векторов в точке $p$ может быть естественным образом отождествлено (путем переноса) с касательным пространством в близлежащей точке $q$ . На общем многообразии нет такого естественного отождествления между близлежащими касательными пространствами, и поэтому касательные векторы в близлежащих точках не могут быть сопоставлены четко определенным образом. Понятие аффинной связности было введено для решения этой проблемы путем соединения близлежащих касательных пространств. Истоки этой идеи можно проследить до двух основных источников: теории поверхностей и тензорного исчисления .

Мотивация из теории поверхности

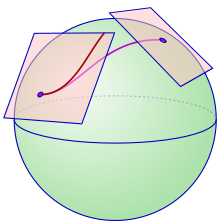
Рассмотрим гладкую поверхность $S$ в трехмерном евклидовом пространстве. Вблизи любой точки $S$ можно аппроксимировать ее касательной плоскостью в этой точке, которая является аффинным подпространством евклидова пространства. Дифференциальные геометры в 19 веке интересовались понятием развертки , в которой одна поверхность катится по другой, без скольжения или скручивания . В частности, касательная плоскость к точке $S$ может быть катится по $S$ : это должно быть легко представить, когда $S$ является поверхностью, подобной 2-сфере, которая является гладкой границей выпуклой области. Когда касательная плоскость катится по $S$ , точка контакта вычерчивает кривую на $S.$ И наоборот, если задана кривая на $S$ , касательную плоскость можно катить по этой кривой. Это дает возможность идентифицировать касательные плоскости в различных точках вдоль кривой: в частности, касательный вектор в касательном пространстве в одной точке кривой идентифицируется с уникальным касательным вектором в любой другой точке кривой. Эти идентификации всегда даются аффинными преобразованиями из одной касательной плоскости в другую.

Это понятие параллельного переноса касательных векторов посредством аффинных преобразований вдоль кривой имеет характерную особенность: точка контакта касательной плоскости с поверхностью всегда перемещается вместе с кривой при параллельном переносе (т. е., когда касательная плоскость катится по поверхности, точка контакта перемещается). Это общее условие характерно для соединений Картана . В более современных подходах точка контакта рассматривается как начало координат в касательной плоскости (которая тогда является векторным пространством), а движение начала координат корректируется переносом, так что параллельный перенос является линейным, а не аффинным.

Однако с точки зрения связности Картана аффинные подпространства евклидова пространства являются модельными поверхностями — они являются простейшими поверхностями в евклидовом 3-пространстве и являются однородными относительно аффинной группы плоскости — и каждая гладкая поверхность имеет единственную модельную поверхность, касательную к ней в каждой точке. Эти модельные поверхности являются геометриями Клейна в смысле Эрлангенской программы Феликса Клейна . В более общем смысле, $n$ -мерное аффинное пространство является геометрией Клейна для аффинной группы $Aff($ $n$ $)$ , причем стабилизатором точки является общая линейная группа $GL($ $n$ $)$ . Тогда аффинное $n$ -многообразие является многообразием, которое выглядит бесконечно мало как $n$ -мерное аффинное пространство.

Мотивация из тензорного исчисления

Вторая мотивация для аффинных связей исходит из понятия ковариантной производной векторных полей. До появления методов, независимых от координат, было необходимо работать с векторными полями, встраивая их соответствующие евклидовы векторы в атлас . Эти компоненты можно дифференцировать, но производные не преобразуются управляемым образом при изменении координат. ^{[ необходима цитата ]} Поправочные члены были введены Элвином Бруно Кристоффелем (следуя идеям Бернхарда Римана ) в 1870-х годах, так что (исправленная) производная одного векторного поля вдоль другого преобразовывалась ковариантно при преобразованиях координат — эти поправочные члены впоследствии стали известны как символы Кристоффеля .

Эта идея была развита в теорию абсолютного дифференциального исчисления (теперь известного как тензорное исчисление ) Грегорио Риччи-Курбастро и его учеником Туллио Леви-Чивита между 1880 годом и началом XX века.

Однако тензорное исчисление по-настоящему ожило с появлением общей теории относительности Альберта Эйнштейна в 1915 году. Через несколько лет после этого Леви-Чивита формализовал уникальную связь, связанную с римановой метрикой, теперь известную как связь Леви-Чивита . Более общие аффинные связи были затем изучены около 1920 года Германом Вейлем ^[5], который разработал подробную математическую основу для общей теории относительности, и Эли Картаном [ ^6], который установил связь с геометрическими идеями, исходящими из теории поверхностей.

Подходы

Сложная история привела к развитию самых разных подходов и обобщений концепции аффинной связности.

Наиболее популярным подходом, вероятно, является определение, мотивированное ковариантными производными. С одной стороны, идеи Вейля были подхвачены физиками в форме калибровочной теории и калибровочно-ковариантных производных . С другой стороны, понятие ковариантного дифференцирования было абстрагировано Жаном-Луи Кошулем , который определил (линейные или кошулевы) связности на векторных расслоениях . На этом языке аффинная связность — это просто ковариантная производная или (линейная) связность на касательном расслоении .

Однако этот подход не объясняет геометрию, стоящую за аффинными связями, и то, как они получили свое название. ^[c] Термин на самом деле берет свое начало в идентификации касательных пространств в евклидовом пространстве с помощью переноса: это свойство означает, что евклидово $n$ -пространство является аффинным пространством . (В качестве альтернативы, евклидово пространство является главным однородным пространством или торсором в группе переносов, которая является подгруппой аффинной группы.) Как упоминалось во введении, есть несколько способов сделать это точным: один использует тот факт, что аффинная связность определяет понятие параллельного переноса векторных полей вдоль кривой. Это также определяет параллельный перенос на расслоении фреймов . Бесконечно малый параллельный перенос в расслоении фреймов дает другое описание аффинной связности, либо как связности Картана для аффинной группы $Aff(n)$ , либо как главной $GL(n)$ связи на расслоении фреймов.

Формальное определение как дифференциального оператора

Пусть $M$ — гладкое многообразие и пусть $Γ(T M)$ — пространство векторных полей на $M$ , то есть пространство гладких сечений касательного расслоения $T M$ . Тогда аффинная связность на $M$ — это билинейное отображение

{\begin{aligned}\Gamma (\mathrm {T} M)\times \Gamma (\mathrm {T} M)&\rightarrow \Gamma (\mathrm {T} M)\\(X,Y )&\mapsto \nabla _{X}Y\,,\end{aligned}}

такой, что для всех $f$ из множества гладких функций на $M$ , записанных как $C \infty (M, R)$ , и всех векторных полей $X, Y$ на $M$ :

$\nabla fX Y = f \nabla X Y$ , то есть $\nabla$ является $C \infty (M, R)$ - линейным по первой переменной;
$\nabla X (fY) = (\partial X f) Y + f \nabla X Y$ , где $\partial X$ обозначает производную по направлению ; то есть $\nabla$ удовлетворяет правилу Лейбница по второй переменной.

Элементарные свойства

Из свойства 1 выше следует, что значение $\nabla X Y$ в точке $x \in M$ зависит только от значения $X$ в точке $x$ , а не от значения $X$ на $M - {x}$ . Из свойства 2 выше также следует, что значение $\nabla X Y$ в точке $x \in M$ зависит только от значения $Y$ на окрестности точки $x$ .
Если $\nabla 1, \nabla 2$ являются аффинными связями, то значение $\nabla$ в точке $x$ $1 х Y - \nabla 2 х Y$ можно записать как $Γ x (X x, Y x)$ , гдеявляется билинейной и гладко зависит от $x$ (т.е. определяет гладкий гомоморфизм расслоений ). Обратно, если $\nabla$ является аффинной связностью, а $Γ$ является таким гладким билинейным гомоморфизмом расслоений (называемым формой связности на $M$ ), то $\nabla + Γ$ является аффинной связностью. $\Gamma _{x}:\mathrm {T} _{x}M\times \mathrm {T} _{x}M\to \mathrm {T} _{x}M$
Если $M$ — открытое подмножество $R n$ , то касательное расслоение $M$ — это тривиальное расслоение $M \times R n$ . В этой ситуации существует каноническая аффинная связность $d$ на $M$ : любое векторное поле $Y$ задается гладкой функцией $V$ из $M$ в $R n$ ; тогда $d X Y$ — векторное поле, соответствующее гладкой функции $d V (X) = \partial X Y$ из $M$ в $R n$ . Любая другая аффинная связность $\nabla$ на $M$ может быть записана как $\nabla = d + Γ$ , где $Γ$ — форма связности на $M$ .
В более общем случае локальная тривиализация касательного расслоения является изоморфизмом расслоений между ограничением $T M$ на открытое подмножество $U$ множества $M$ и $U \times R n$ . Ограничение аффинной связности $\nabla$ на $U$ может быть тогда записано в виде $d + Γ,$ где $Γ$ — форма связности на $U$ .

Параллельный транспорт для аффинных соединений

Сравнение касательных векторов в разных точках многообразия, как правило, не является четко определенным процессом. Аффинное соединение предоставляет один из способов исправить это, используя понятие параллельного переноса , и, действительно, это может быть использовано для определения аффинного соединения.

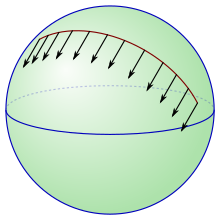
Пусть $M$ — многообразие с аффинной связностью $\nabla$ . Тогда векторное поле $X$ называется параллельным , если $\nabla X = 0$ в том смысле, что для любого векторного поля $Y$ , $\nabla Y X = 0.$ Интуитивно говоря, параллельные векторы имеют все свои производные, равные нулю , и поэтому в некотором смысле являются постоянными . Оценивая параллельное векторное поле в двух точках $x$ и $y$ , получается отождествление между касательным вектором в точке $x$ и одним в точке $y$ . Такие касательные векторы называются параллельными переносами друг друга.

Ненулевые параллельные векторные поля, вообще говоря, не существуют, поскольку уравнение $\nabla X = 0$ является частным дифференциальным уравнением , которое переопределено : условием интегрируемости для этого уравнения является обращение в нуль кривизны $\nabla$ (см. ниже). Однако, если это уравнение ограничить кривой от x до y $,$ оно становится обыкновенным дифференциальным уравнением . Тогда существует единственное решение для любого начального значения $X$ $в$ точке $x$ .

Точнее, если $γ : I \to M$ — гладкая кривая, параметризованная интервалом $[a, b]$ и $ξ \in T x M$ , где $x = γ (a)$ , то векторное поле $X$ вдоль $γ$ (и, в частности, значение этого векторного поля при $y = γ (b)$ ) называется параллельным переносом $ξ$ вдоль $γ,$ если

$\nabla γ' (t) X = 0$ , для всех $t \in [a, b]$
$Xγ (a) = ξ$ . $$

Формально первое условие означает, что $X$ параллельно относительно связности обратного проецирования на расслоении обратного проецирования $γ * T M$ . Однако в локальной тривиализации это система линейных обыкновенных дифференциальных уравнений первого порядка , которая имеет единственное решение для любого начального условия, заданного вторым условием (например, теоремой Пикара–Линделёфа ).

Таким образом, параллельный перенос обеспечивает способ перемещения касательных векторов вдоль кривой с использованием аффинной связи, чтобы они «указывали в одном направлении» в интуитивном смысле, и это обеспечивает линейный изоморфизм между касательными пространствами на двух концах кривой. Изоморфизм, полученный таким образом, будет в общем случае зависеть от выбора кривой: если это не так, то параллельный перенос вдоль каждой кривой может использоваться для определения параллельных векторных полей на $M$ , что может произойти только в том случае, если кривизна $\nabla$ равна нулю.

Линейный изоморфизм определяется его действием на упорядоченном базисе или фрейме . Следовательно, параллельный перенос можно также охарактеризовать как способ переноса элементов (касательного) расслоения фрейма $GL(M)$ вдоль кривой. Другими словами, аффинная связность обеспечивает подъем любой кривой $γ$ в $M$ до кривой $γ̃$ в $GL(M)$ .

Формальное определение рамочного пучка

Аффинную связность можно также определить как главную $GL(n)$ связность $ω$ на расслоении фреймов $F M$ или $GL(M)$ многообразия $M$ . Более подробно, $ω$ — это гладкое отображение из касательного расслоения $T(F M)$ расслоения фреймов в пространство матриц $n \times n$ (которое является алгеброй Ли $gl (n)$ группы Ли $GL(n)$ обратимых матриц $n \times n$ ), удовлетворяющее двум свойствам:

$ω$ эквивариантна относительно действия $GL($ $n$ $)$ на $T($ F $M$ $)$ и $gl$ $($ $n$ ) $;$
$ω (X ξ) = ξ$ для любого $ξ$ из $gl (n)$ , где $X ξ$ — векторное поле на $F M ,$ соответствующее $ξ$ .

Такая связь $ω$ немедленно определяет ковариантную производную не только на касательном расслоении, но и на векторных расслоениях, связанных с любым групповым представлением GL $(n)$ , включая расслоения тензоров и тензорных плотностей . Наоборот, аффинная связь на касательном расслоении определяет аффинную связь на расслоении фрейма, например, требуя, чтобы $ω$ обращалась в нуль на касательных векторах к подъемам кривых в расслоение фрейма, определенное параллельным переносом.

Рамочный пучок также оснащен формой припоя $θ : T(F M) \to R n$ , которая горизонтальна в том смысле, что она исчезает на вертикальных векторах, таких как точечные значения векторных полей $X ξ$ : Действительно, $θ$ определяется сначала путем проецирования касательного вектора (к $F M$ в системе $f$ ) на $M$ , а затем путем взятия компонентов этого касательного вектора на $M$ относительно системы $f$ . Обратите внимание, что $θ$ также является $GL(n)$ -эквивариантным (где $GL(n)$ действует на $R n$ путем умножения матриц).

Пара $(θ, ω)$ определяет изоморфизм расслоений $T(F M)$ с тривиальным расслоением $F M \times aff (n)$ , где $aff (n)$ — декартово произведение $R n$ и $gl (n)$ (рассматриваемое как алгебра Ли аффинной группы, которая на самом деле является полупрямым произведением — см. ниже).

Аффинные связи как связи Картана

Аффинные связности могут быть определены в рамках общей структуры Картана. ^[7] В современном подходе это тесно связано с определением аффинных связностей на расслоении фреймов. Действительно, в одной формулировке связность Картана является абсолютным параллелизмом главного расслоения, удовлетворяющего подходящим свойствам. С этой точки зрения $aff (n)$ -значная одномерная форма $(θ, ω) : T(F M) \to aff (n)$ на расслоении фреймов (аффинного многообразия ) является связностью Картана. Однако первоначальный подход Картана отличался от этого в ряде отношений:

понятия каркасных пучков или главных пучков не существовало;
связь рассматривалась с точки зрения параллельного переноса между бесконечно близкими точками; ^[d]
этот параллельный перенос был аффинным, а не линейным;
перемещаемые объекты не были касательными векторами в современном смысле, а элементами аффинного пространства с отмеченной точкой, которую картановская связь в конечном итоге отождествляет с касательным пространством.

Объяснения и историческая интуиция

Только что поднятые вопросы проще всего объяснить в обратном порядке, начиная с мотивации, предоставленной теорией поверхности. В этой ситуации, хотя плоскости, прокатываемые по поверхности, являются касательными плоскостями в наивном смысле, понятие касательного пространства на самом деле является бесконечно малым понятием, ^[e], тогда как плоскости, как аффинные подпространства R $3$ , имеют бесконечную протяженность. Однако все эти аффинные плоскости имеют отмеченную точку, точку контакта с поверхностью, и они касаются поверхности в этой точке. Поэтому возникает путаница $,$ поскольку аффинное пространство с отмеченной точкой можно отождествить с его касательным пространством в этой точке. Однако параллельный перенос, определяемый прокаткой, не фиксирует это начало координат: он аффинный , а не линейный; линейный параллельный перенос можно восстановить, применив перенос.

Абстрагируя эту идею, аффинное многообразие должно быть $n$ -многообразием $M$ с аффинным пространством $A x$ размерности $n$ , прикрепленным к каждому $x \in M$ в отмеченной точке $a x \in A x$ , вместе с методом переноса элементов этих аффинных пространств вдоль любой кривой $C$ в $M$ . Этот метод должен удовлетворять нескольким свойствам:

для любых двух точек $x, y$ на $C$ параллельный перенос является аффинным преобразованием из $A x$ в $A y$ ;
параллельный перенос определяется бесконечно мало в том смысле, что он дифференцируем в любой точке $C$ и зависит только от касательного вектора к $C$ в этой точке;
производная параллельного переноса в точке $x$ определяет линейный изоморфизм из $T x M$ в $T a x A x$ .

Эти два последних пункта довольно трудно сделать точными, ^[9] поэтому аффинные связи чаще определяются бесконечно малыми. Чтобы мотивировать это, достаточно рассмотреть, как аффинные системы отсчета преобразуются бесконечно малыми относительно параллельного переноса. (Это является источником метода движущихся систем Картана. $)$ Аффинная система в точке состоит из списка $(p, e1,\dots en),$ где $p \in Ax$ ^[f] $,$ а $ei$ образуют базис $Tp (Ax) . Затем аффинная связь задается символически с$ $помощью$ дифференциальной системы первого порядка

(*){\begin{cases}\mathrm {d} {p}&=\theta ^{1}\mathbf {e} _{1}+\cdots +\theta ^{n}\mathbf { e} _{n}\\\mathrm {d} \mathbf {e} _{i}&=\omega _{i}^{1}\mathbf {e} _{1}+\cdots +\omega _ {i}^{n}\mathbf {e} _{n}\end{cases}}\quad i=1,2,\ldots,n

определяется набором единичных форм $(θ j, ω джи я)$ . Геометрически аффинный фрейм претерпевает смещение, перемещаясь вдоль кривой $γ$ от $γ (t)$ до $γ (t + δt),$ заданное (приблизительно или бесконечно мало) как

{\begin{aligned}p(\gamma (t+\delta t)) -p(\gamma (t))&=\left(\theta ^{1}\left(\gamma '(t)\ right)\mathbf {e} _{1}+\cdots +\theta ^{n}\left(\gamma '(t)\right)\mathbf {e} _{n}\right)\mathrm {\delta } t\\\mathbf {e} _{i}(\gamma (t+\delta t))-\mathbf {e} _{i}(\gamma (t))&=\left(\omega _{i }^{1}\left(\gamma '(t)\right)\mathbf {e} _{1}+\cdots +\omega _{i}^{n}\left(\gamma '(t)\right)\mathbf {e} _{n}\right)\delta t\,.\end{align}}

Более того, аффинные пространства $A x$ должны быть касательными к $M$ в неформальном смысле, что смещение $a x$ вдоль $γ$ может быть отождествлено (приблизительно или бесконечно мало) с касательным вектором $γ'(t)$ к $γ$ в точке $x = γ (t)$ (который является бесконечно малым смещением $x$ ). Поскольку

a_{x}(\gamma (t+\delta t))-a_{x}(\gamma (t))=\theta \left(\gamma '(t)\right)\delta t\,,

где $θ$ определяется как $θ (X) = θ 1 (X) e 1 + \dots + θ n (X) e n$ , эта идентификация задается с помощью $θ$ , поэтому требование состоит в том, чтобы $θ$ был линейным изоморфизмом в каждой точке.

$Таким образом$ , тангенциальное аффинное пространство $A x$ интуитивно отождествляется с бесконечно малой аффинной окрестностью x .

Современная точка зрения делает всю эту интуицию более точной, используя главные расслоения (основная идея состоит в замене фрейма или переменного фрейма пространством всех фреймов и функций на этом пространстве). Она также черпает вдохновение из программы Феликса Клейна в Эрлангене ^[10] , в которой геометрия определяется как однородное пространство . Аффинное пространство является геометрией в этом смысле и снабжено плоской связностью Картана. Таким образом, общее аффинное многообразие рассматривается как искривленная деформация плоской модельной геометрии аффинного пространства.

Аффинное пространство как плоская модельная геометрия

Определение аффинного пространства

Неформально, аффинное пространство — это векторное пространство без фиксированного выбора начала координат . Оно описывает геометрию точек и свободных векторов в пространстве. Вследствие отсутствия начала координат точки в аффинном пространстве не могут быть сложены вместе, поскольку это требует выбора начала координат, с которым можно сформировать закон параллелограмма для сложения векторов. Однако вектор $v$ может быть добавлен к точке $p$ путем помещения начальной точки вектора в $p$ и последующего переноса $p$ в конечную точку. Описанная таким образом операция $p \to p + v$ — это перенос p вдоль $v$ . В технических терминах аффинное $n$ $-пространство$ — это множество $A$ $n ,$ снабженное свободным транзитивным действием векторной группы $R$ $n$ на нем посредством этой операции переноса точек: $A$ $n$ является, таким образом, главным однородным пространством для векторной группы $R$ $n$ .

Общая линейная группа $GL(n)$ — это группа преобразований R $n$ $,$ которые сохраняют линейную структуру R $n$ в том смысле, что $T (av + bw) = aT (v) + bT (w) .$ $По$ аналогии, аффинная группа $Aff(n)$ — это группа преобразований $A n ,$ сохраняющих аффинную структуру . Таким образом, $φ \in Aff(n)$ должно сохранять трансляции в том смысле, что

{\ displaystyle \ varphi (p + v) = \ varphi (p) + T (v)}

где $T$ — общее линейное преобразование. Отображение, переводящее $φ \in Aff(n)$ в $T \in GL(n)$ — это гомоморфизм групп . Его ядро — группа трансляций $R n$ . Стабилизатор любой точки $p$ в $A$ можно, таким образом, отождествить с $GL(n)$ с помощью этой проекции: это реализует аффинную группу как полупрямое произведение GL $(n)$ и $R n$ , а аффинное пространство — как однородное пространство $Aff(n)/GL(n)$ .

Аффинные фреймы и плоская аффинная связность

Аффинный фрейм для $A$ состоит из точки $p \in A$ и базиса $(e 1,\dots e n)$ векторного пространства $T p A = R n$ . Общая линейная группа $GL(n)$ действует свободно на множестве $F A$ всех аффинных фреймов, фиксируя $p$ и преобразуя базис $(e 1,\dots e n)$ обычным образом, а отображение $π,$ переводящее аффинный фрейм $(p; e 1,\dots e n)$ в $p,$ является отображением факторизации . Таким образом, $F A$ является главным $GL(n)$ -расслоением над $A$ . Действие $GL(n)$ естественным образом продолжается до свободного транзитивного действия аффинной группы $Aff($ n ) на F A , так что F A является Aff( n ) -торсором $,$ $а$ выбор $системы отсчета$ отождествляет $F A$ → $A с главным$ расслоением Aff $($ $n$ $)$ $\to$ Aff $($ $n$ $)$ $/$ $GL($ $n$ $)$ .

На $F A$ имеется набор из $n + 1$ функций, определяемых формулой

\pi (p;\mathbf {e} _{1},\dots,\mathbf {e} _{n})=p

(как и прежде) и

{\ displaystyle \varepsilon _ {i} (p; \ mathbf {e} _ {1}, \ dots, \ mathbf {e} _ {n}) = \ mathbf {e} _ {i} \,.}

После выбора базовой точки для $A$ все они являются функциями со значениями в $R n$ , поэтому можно взять их внешние производные , чтобы получить дифференциальные 1-формы со значениями в $R n$ . Поскольку функции $ε i$ дают базис для $R n$ в каждой точке $F A$ , эти 1-формы должны быть выражены как суммы вида

{\begin{align}\mathrm {d} \pi &=\theta ^{1}\varepsilon _{1}+\cdots +\theta ^{n}\varepsilon _{n}\\\mathrm {d} \varepsilon _{i}&=\omega _{i}^{1}\varepsilon _{1}+\cdots +\omega _{i}^{n}\varepsilon _{n}\end{align}}

для некоторого набора $(θ i, ω к дж) 1 \leq i, j, k \leq n$ вещественнозначных 1-форм на $Aff(n)$ . Эта система 1-форм на главном расслоении $F A \to A$ определяет аффинную связность на $A$ .

Беря внешнюю производную второй раз и используя тот факт, что $d 2 = 0,$ $а$ также линейную независимость ε $i$ , получаем следующие соотношения:

{\begin{align}\mathrm {d} \theta ^{j}-\sum _{i}\omega _{i}^{j}\wedge \theta ^{i}&=0\\\mathrm {d} \omega _{i}^{j}-\sum _{k}\omega _{k}^{j}\wedge \omega _{i}^{k}&=0\,.\end{align}}

Это уравнения Маурера–Картана для группы Ли $Aff(n)$ (отождествленной с $F A$ выбором системы отсчета). Кроме того:

Пфаффова система $θ j = 0$ (для всех $j$ ) интегрируема , а ее интегральные многообразия являются слоями главного расслоения $Aff(n) \to A$ .
система Пфаффа $ω джи я = 0$ (для всех $i, j$ ) также интегрируемо, и его интегральные многообразия определяют параллельный перенос в $F A$ .

Таким образом, формы $(ω джи я)$ определяют плоскую главную связность на $F A \to A$ .

Для строгого сравнения с мотивировкой следует фактически определить параллельный перенос в главном $Aff(n)$ -расслоении над $A$ . Это можно сделать, оттянув $F A$ с помощью гладкого отображения $φ : R n \times A \to A$ , определенного переносом. Тогда композит $φ' * F A \to F A \to A$ является главным $Aff(n)$ -расслоением над $A$ , а формы $(θ i, ω к дж)$ оттягиваемся назад, чтобы получить плоскую главную $Aff(n)$ -связность на этом расслоении.

Общие аффинные геометрии: формальные определения

Аффинное пространство, как и любая гладкая геометрия Клейна , представляет собой многообразие, снабженное плоской связностью Картана. Более общие аффинные многообразия или аффинные геометрии легко получаются путем отказа от условия плоскостности, выраженного уравнениями Маурера-Картана. Существует несколько способов приблизиться к определению, и два из них будут даны. Оба определения облегчаются осознанием того, что 1-формы $(θ i, ω к дж)$ в плоской модели объединяются, давая 1-форму со значениями в алгебре Ли $aff (n)$ аффинной группы $Aff(n)$ .

В этих определениях $M$ — гладкое $n$ -многообразие, а $A = Aff(n)/GL(n)$ — аффинное пространство той же размерности.

Определение через абсолютный параллелизм

Пусть $M$ — многообразие, а $P$ — главное $GL(n)$ -расслоение над $M.$ Тогда аффинная связность — это 1-форма $η$ на $P$ со значениями в $aff (n),$ удовлетворяющая следующим свойствам:

$η$ эквивариантно относительно действия $GL(n)$ на $P$ и $aff (n)$ ;
$η (X ξ) = ξ$ для всех $ξ$ в алгебре Ли $gl (n)$ всехматриц $размера n \times n ;$
$η$ — линейный изоморфизм каждого касательного пространства $P$ с $aff (n)$ .

Последнее условие означает, что $η$ является абсолютным параллелизмом на $P$ , т. е. он отождествляет касательное расслоение $P$ с тривиальным расслоением (в данном случае $P \times aff (n)$ ). Пара $(P, η)$ определяет структуру аффинной геометрии на $M$ , превращая ее в аффинное многообразие .

Аффинная алгебра Ли $aff (n)$ расщепляется как полупрямое произведение $R n$ и $gl (n),$ и поэтому $η$ может быть записана как пара $(θ, ω)$ , где $θ$ принимает значения в $R n$ , а $ω$ принимает значения в $gl (n)$ . Условия 1 и 2 эквивалентны тому, что $ω$ является главной $GL(n)$ -связностью, а $θ$ является горизонтальной эквивариантной 1-формой, которая индуцирует гомоморфизм расслоений из $T M$ в ассоциированное расслоение $P \times GL(n) R n$ . Условие 3 эквивалентно тому факту, что этот гомоморфизм расслоений является изоморфизмом. (Однако это разложение является следствием довольно специальной структуры аффинной группы.) Поскольку $P$ является расслоением фреймов $P \times GL(n) R n$ , отсюда следует, что $θ$ обеспечивает изоморфизм расслоений между $P$ и расслоением фреймов $F M$ алгебры $M$ ; это восстанавливает определение аффинной связности как главной $GL(n)$ -связности на $F M$ .

1-формы, возникающие в плоской модели, являются просто компонентами $θ$ и $ω$ .

Определение как главная аффинная связь

Аффинная связность на $M$ — это главное $Aff(n)$ -расслоение $Q$ над $M$ вместе с главным $GL(n)$ -подрасслоением $P$ Q и главной $Aff($ $n$ $)$ -связностью $α$ (1-формой на $Q$ со значениями в $aff$ $($ $n$ $)$ ), которая удовлетворяет следующему (общему) условию Картана . Компонента $R$ $n$ обратного проецирования $α$ на $P является$ $горизонтальной$ эквивариантной 1-формой и, таким образом, определяет гомоморфизм расслоения из $T$ $M$ в $P$ $\times$ $GL($ $n$ $)$ $R$ $n$ : это требуется для изоморфизма.

Отношение к мотивации

Так как $Aff(n)$ действует на $A$ , то с главным расслоением $Q$ связано расслоение $A = Q \times Aff(n) A$ , которое является расслоением над $M ,$ расслоение которого в точке $x$ в $M$ является аффинным пространством $A x$ . Сечение $a$ расслоения $A$ (определяющее отмеченную точку $a x$ в $A x$ для каждого $x \in M$ ) определяет главное $GL(n)$ -подрасслоение $P$ расслоения $Q$ (как расслоение стабилизаторов этих отмеченных точек) и наоборот. Главное соединение $α$ определяет связность Эресмана на этом расслоении, следовательно, понятие параллельного переноса. Условие Картана гарантирует, что выделенное сечение $a$ всегда движется при параллельном переносе.

Дополнительные свойства

Кривизна и кручение

Кривизна и кручение являются основными инвариантами аффинной связности. Поскольку существует множество эквивалентных способов определения понятия аффинной связности, существует множество различных способов определения кривизны и кручения.

С точки зрения связности Картана кривизна — это неспособность аффинной связности $η$ удовлетворить уравнению Маурера–Картана

\mathrm {d} \eta + {\tfrac {1}{2}}[\eta \wedge \eta ]=0,

где второй член в левой части — это произведение клина, использующее скобку Ли в $aff (n)$ для сжатия значений. Разлагая $η$ в пару $(θ, ω)$ и используя структуру алгебры Ли $aff (n)$ , эту левую часть можно разложить в две формулы

\mathrm {d} \theta +\omega \wedge \theta \quad {\text{и}}\quad \mathrm {d} \omega +\omega \wedge \omega \,,

где клиновые произведения оцениваются с помощью умножения матриц. Первое выражение называется кручением соединения , а второе также называется кривизной.

Эти выражения являются дифференциальными 2-формами на общем пространстве расслоения фреймов. Однако они горизонтальны и эквивариантны, и, следовательно, определяют тензорные объекты. Их можно определить непосредственно из индуцированной ковариантной производной $\nabla$ на $T M$ следующим образом.

Кручение определяется по формуле

T^{\nabla }(X,Y)=\nabla _{X}Y-\nabla _{Y}X-[X,Y].

Если кручение исчезает, то соединение называется свободным от кручения или симметричным .

Кривизна определяется по формуле

R_{X,Y}^{\nabla }Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X ,Y]}Z.

Обратите внимание, что $[X, Y]$ — это скобка Ли векторных полей.

[X,Y]=\left(X^{j}\partial _{j}Y^{i}-Y^{j}\partial _{j}X^{i}\right)\partial _{i}

в обозначениях Эйнштейна . Это не зависит от выбора системы координат и

\partial _{i}=\left({\frac {\partial }{\partial \xi ^{i}}}\right)_{p}\,,

касательный вектор в точке $p i$ - $й$ координатной кривой . $\partial$ $i$ являются естественным базисом для касательного пространства в точке $p$ , а $X$ $i —$ соответствующие координаты для векторного поля $X$ $=$ $X$ $i$ $\partial$ $i$ .

Когда и кривизна, и кручение обращаются в нуль, связь определяет структуру предалгебры Ли на пространстве глобальных сечений касательного расслоения.

Связь Леви-Чивита

Если $(M, g)$ — риманово многообразие , то на $M$ существует единственная аффинная связность $\nabla$ со следующими двумя свойствами:

связность не имеет кручения, т. е. $T \nabla$ равен нулю, так что $\nabla X Y - \nabla Y X = [X, Y]$ ;
параллельный перенос является изометрией, т.е. внутренние произведения (определяемые с помощью $g$ ) между касательными векторами сохраняются.

Эта связь называется связью Леви-Чивиты .

Термин «симметричный» часто используется вместо термина «без кручения» для первого свойства. Второе условие означает, что связь является метрической в том смысле, что риманова метрика $g$ параллельна: $\nabla g = 0.$ Для связи без кручения условие эквивалентно тождеству $X g (Y, Z)$ = $g (\nabla X Y, Z)$ + $g (Y, \nabla X Z)$ , «совместимость с метрикой». ^[11] В локальных координатах компоненты формы называются символами Кристоффеля : из-за уникальности связности Леви-Чивиты существует формула для этих компонент в терминах компонентов $g$ .

Геодезические

Поскольку прямые линии являются концепцией в аффинной геометрии, аффинные связности определяют обобщенное понятие (параметризованных) прямых линий на любом аффинном многообразии, называемых аффинными геодезическими. Абстрактно, параметрическая кривая $γ : I \to M$ является прямой, если ее касательный вектор остается параллельным и равнозначным себе при переносе вдоль $γ$ . С линейной точки зрения аффинная связность $M$ различает аффинные геодезические следующим образом: гладкая кривая $γ : I \to M$ является аффинной геодезической, если она параллельно переносится вдоль $γ$ , то есть ${\dot {\gamma }}$

\tau _{t}^{s}{\dot {\gamma }}(s)={\dot {\gamma }}(t)

где $τ с т : T γ s M \to T γ t M$ — это карта параллельного переноса, определяющая соединение.

В терминах бесконечно малой связи $\nabla$ производная этого уравнения подразумевает

\nabla _{{\dot {\gamma }}(t)}{\dot {\gamma }}(t)=0

для всех $t \in I$ .

Наоборот, любое решение этого дифференциального уравнения дает кривую, касательный вектор которой параллельно переносится вдоль кривой. Для каждого $x \in M$ и каждого $X \in T x M$ существует единственная аффинная геодезическая $γ : I \to M$ с $γ (0) = x$ и $γ̇ (0) = X$ и где $I$ — максимальный открытый интервал в $R$ , содержащий 0, на котором определена геодезическая. Это следует из теоремы Пикара–Линделёфа и позволяет определить экспоненциальное отображение, связанное с аффинной связностью.

В частности, когда $M$ — ( псевдо ) риманово многообразие , а $\nabla$ — связность Леви-Чивиты , то аффинные геодезические являются обычными геодезическими римановой геометрии и представляют собой кривые, минимизирующие локальное расстояние.

Определенные здесь геодезические иногда называют аффинно параметризованными , поскольку заданная прямая в $M$ определяет параметрическую кривую $γ$ через линию вплоть до выбора аффинной репараметризации $γ (t) \to γ (at + b)$ , где $a$ и $b$ являются константами. Касательный вектор к аффинной геодезической параллелен и равнополочен вдоль себя. Непараметризованная геодезическая или та, которая просто параллельна вдоль себя, не обязательно равнополочен, должна удовлетворять только

\nabla _{\dot {\gamma }}{\dot {\gamma }}=k{\dot {\gamma }}

для некоторой функции $k,$ определенной вдоль $γ$ . Непараметризованные геодезические часто изучаются с точки зрения проективных связностей .

Разработка

Аффинная связность определяет понятие развёртки кривых. Интуитивно, развёртка охватывает понятие, что если $x t$ является кривой в $M$ , то аффинное касательное пространство в точке $x 0$ может быть прокатано вдоль кривой. При этом отмеченная точка контакта между касательным пространством и многообразием вычерчивает кривую $C t$ в этом аффинном пространстве: развёртку $x t$ .

Формально, пусть $τ 0 т : T x t M \to T x 0 M$ — линейное параллельное транспортное отображение, связанное с аффинной связностью. Тогда развертка $C t$ — это кривая в $T x 0 M$ , которая начинается в 0 и параллельна касательной к $x t$ для всего времени $t$ :

{\dot {C}}_{t}=\tau _{t}^{0}{\dot {x}}_{t}\,,\quad C_{0}=0.

В частности, $x t$ является геодезической тогда и только тогда, когда ее развертка является аффинно параметризованной прямой в $T x 0 M$ . ^[12]

Пересмотр теории поверхности

Если $M$ — поверхность в $R 3$ , то легко видеть, что $M$ имеет естественную аффинную связность. С точки зрения линейной связности ковариантная производная векторного поля определяется путем дифференцирования векторного поля, рассматриваемого как отображение из $M$ в $R 3$ , и последующего ортогонального проецирования результата обратно на касательные пространства $M$ . Легко видеть, что эта аффинная связность не имеет кручения. Более того, это метрическая связность относительно римановой метрики на $M,$ индуцированной скалярным произведением на $R 3$ , следовательно, это связность Леви-Чивиты этой метрики.

Пример: единичная сфера в евклидовом пространстве

Пусть $⟨ , ⟩$ — обычное скалярное произведение на $R 3$ , а $S 2$ — единичная сфера. Касательное пространство к $S 2$ в точке $x$ естественным образом отождествляется с векторным подпространством $R 3 ,$ состоящим из всех векторов, ортогональных $x$ . Из этого следует, что векторное поле $Y$ на $S 2$ можно рассматривать как отображение $Y : S 2 \to R 3 ,$ которое удовлетворяет

\langle Y_{x},x\rangle =0\,,\quad \forall x\in \mathbf {S} ^{2}.

Обозначим как $d Y$ дифференциал (матрицу Якоби) такого отображения. Тогда имеем:

Лемма . Формула

(\nabla _{Z}Y)_{x}=\mathrm {d} Y_{x}(Z_{x})+\langle Z_{x},Y_{x}\rangle x

определяет аффинную связность на

S2

с нулевым кручением

.

Доказательство . Несложно доказать, что

\nabla

удовлетворяет тождеству Лейбница и является

C \infty (S 2)

линейным по первой переменной. Поэтому все, что нужно доказать здесь, это то, что отображение выше действительно определяет касательное векторное поле. То есть, нам нужно доказать, что для всех

x

S 2

{\bigl \langle }(\nabla _{Z}Y)_{x},x{\bigr \rangle }=0\,.\qquad {\text{(Eq.1)}}

Рассмотрите карту

{\begin{aligned}f:\mathbf {S} ^{2}&\to \mathbf {R} \\x&\mapsto \langle Y_{x},x\rangle \,.\end{aligned}}

Отображение f постоянно, поэтому его дифференциал равен нулю. В частности,

\mathrm {d} f_{x}(Z_{x})={\bigl \langle }(\mathrm {d} Y)_{x}(Z_{x}),x(\gamma '(t)){\bigr \rangle }+\langle Y_{x},Z_{x}\rangle =0\,.

Далее следует уравнение 1 выше. QED

Смотрите также

Примечания

^ Линейную связь также часто называют аффинной связью или просто связью , ^[1] так что нет единого мнения о точных определениях этих терминов (Джон М. Ли называет ее просто связью ). ^[2]
^ Картан объясняет, что он заимствовал этот термин (т. е. «аффинная связь») из книги Г. Вейля и ссылался на него ( Пространство-Время-Материя ), хотя он использовал его в более общем контексте. ^[4]
^ В результате многие математики используют термин линейная связность (вместо аффинной связности ) для связности на касательном расслоении на том основании, что параллельный перенос является линейным, а не аффинным. Однако то же самое свойство сохраняется для любой связности (Кошюля или линейной Эресмана) на векторном расслоении . Первоначально термин аффинная связность является сокращением от аффинной связности в смысле Картана, и это подразумевает, что связность определена на касательном расслоении, а не на произвольном векторном расслоении. Понятие линейной связности Картана на самом деле не имеет особого смысла, поскольку линейные представления не являются транзитивными.
^ Трудно сделать интуицию Картана точной, не прибегая к гладкому анализу бесконечно малых , но один из способов — считать его точки переменными , то есть отображениями из некоторого невидимого пространства параметров в многообразие, которое затем можно дифференцировать.
^ Классически касательное пространство рассматривалось как бесконечно малое приближение, в то время как в современной дифференциальной геометрии касательные пространства часто определяются в терминах дифференциальных объектов, таких как производные. ^[8]
^ Это можно рассматривать как выбор источника: на самом деле достаточно рассмотреть только случай $p = a x$ ; Картан неявно отождествляет его с $x$ в $M$ .

Цитаты

↑ Ли 1997, стр. 51.
^ Ли 2018, стр. 91.
^ Ли 2018, стр. 88, Связи.
^ Акивис и Розенфельд 1993, стр. 213.
↑ Weyl 1918, 5 изданий до 1922 года.
↑ Картан 1923.
↑ Картан 1926.
^ Кобаяши и Номидзу 1996, Том 1, разделы 1.1–1.2
^ Подробнее см. Lumiste (2001b). Следующая интуитивная трактовка — это трактовка Картана (1923) и Картана (1926).
↑ См. R. Hermann (1983), Приложение 1–3 к Cartan (1951), а также Sharpe (1997).
^ Кобаяши и Номидзу 1996, стр. 160, Том. я
^ Эта трактовка развития взята из Kobayashi & Nomizu (1996, Volume 1, Proposition III.3.1); см. раздел III.3 для более геометрического рассмотрения. См. также Sharpe (1997) для подробного обсуждения развития в других геометрических ситуациях.

Ссылки

Акивис, MA; Розенфельд, Борис (1993). Эли Картан (1869–1951). Перевод Голдберга, В. В. AMS . ISBN 978-0-8218-5355-9.
Ли, Джон М. (1997). Римановы многообразия: введение в кривизну . Graduate Texts in Mathematics . Vol. 176. New York: Springer-Verlag . ISBN 978-0-387-98322-6. OCLC 54850593.
Ли, Джон М. (2018). Введение в римановы многообразия. Graduate Texts in Mathematics. Том 176 (2-е изд.). Springer Verlag . doi :10.1007/978-3-319-91755-9. ISBN 978-3-319-91755-9.

Библиография

Основные исторические ссылки

Кристоффель, Элвин Бруно (1869), «Über die Transformation der homogenen Differentialausdrücke zweiten Grades», Journal für die reine und angewandte Mathematik , 1869 (70): 46–70, doi : 10.1515/crll.1869.70.46, S2CID 122999847
Леви-Чивита, Туллио (1917), «Nozione di Parallismo in una varietà qualunque e conseguente specazione geometry della curvatura Riemanniana», Rend. Цирк. Мат. Палермо , 42 : 173–205, номер документа : 10.1007/bf03014898, S2CID 122088291 .
Картан, Эли (1923), «Sur les variétés à connexion affine, et la theorie de la relativité généralisée (première party)», Annales Scientifiques de l'École Normale Supérieure , 40 : 325–412, doi : 10.24033/asens.751
Картан, Эли (1924), «Sur les variétés à connexion affine, et la theorie de la relativité généralisée (première party) (Suite)», Annales Scientifiques de l'École Normale Supérieure , 41 : 1–25, doi : 10.24033/ asens.753
Картан, Эли (1986), О многообразиях с аффинной связностью и общей теории относительности , Humanities Press

Трактовка Картаном аффинных связей, мотивированная изучением теории относительности. Включает подробное обсуждение физики систем отсчета и того, как связь отражает физическое понятие переноса вдоль мировой линии .

Картан, Эли (1926), «Пространства аффинной, проективной и конформной связи», Acta Math. , 48 : 1–42, doi : 10.1007/BF02629755

Более математически мотивированное описание аффинных связей.

Картан, Эли (1951), с приложениями Роберта Германа (редактор), Геометрия римановых пространств (перевод Джеймса Глейзбрука из Leçons sur la géométrie des espaces de Riemann , 2-е изд.), Math Sci Press, Массачусетс (опубликовано в 1983 г.) , ISBN 978-0-915692-34-7.

Аффинные связности с точки зрения римановой геометрии . В приложениях Роберта Германа обсуждается мотивация из теории поверхностей, а также понятие аффинных связностей в современном смысле Кошуля. Он развивает основные свойства дифференциального оператора ∇ и связывает их с классическими аффинными связностями в смысле Картана.

Weyl, Hermann (1918), Raum, Zeit, Materie (5 изданий до 1922 г., с примечаниями Юргена Элерса (1980 г.), перевод 4-го издания Space, Time, Matter Генри Брозе, 1922 г. (ред. Метуэн, переиздано в 1952 г. Дувром), Springer, Берлин, ISBN 0-486-60267-2

Вторичные ссылки

Кобаяси, Сёсичи; Номидзу, Кацуми (1996), Основы дифференциальной геометрии, т. 1 и 2 (новое издание), Wiley-Interscience, ISBN 0-471-15733-3.

Это основная ссылка на технические детали статьи. Том 1, глава III дает подробный отчет об аффинных связностях с точки зрения главных расслоений на многообразии, параллельного переноса, развертки, геодезических и связанных дифференциальных операторов. Том 1, глава VI дает отчет об аффинных преобразованиях, кручении и общей теории аффинной геодезии. Том 2 дает ряд приложений аффинных связностей к однородным пространствам и комплексным многообразиям , а также к другим различным темам.

Лумисте, Юло (2001a) [1994], «Аффинная связь», в Хазевинкеле, Михиэле (редактор), Энциклопедия математики , EMS Press , ISBN 978-1-55608-010-4.
Лумисте, Юло (2001b) [1994], «Связи на многообразии», в Хазевинкель, Михил (ред.), Энциклопедия математики , EMS Press , ISBN 978-1-55608-010-4.

Две статьи Лумисте, дающие точные условия на параллельных транспортных отображениях, чтобы они определяли аффинные связи. Они также рассматривают кривизну, кручение и другие стандартные темы с классической (неглавной пучковой) точки зрения.

Шарп, RW (1997), Дифференциальная геометрия: обобщение Картана программы Эрлангена Кляйна , Springer-Verlag, Нью-Йорк, ISBN 0-387-94732-9.

Это заполняет некоторые исторические детали и обеспечивает более удобный для читателя элементарный отчет о связях Картана в целом. Приложение A проясняет связь между точками зрения на главную связность и абсолютный параллелизм. Приложение B заполняет разрыв между классической «катящейся» моделью аффинных связностей и современной моделью, основанной на главных расслоениях и дифференциальных операторах.