Выборка (обработка сигнала)

Измерение сигнала в дискретные интервалы времени

Представление выборки сигнала. Непрерывный сигнал S ( t ) представлен зеленой линией, а дискретные выборки обозначены синими вертикальными линиями.

В обработке сигналов выборка — это преобразование непрерывного сигнала в дискретный сигнал . Типичным примером является преобразование звуковой волны в последовательность «выборок». Выборка — это значение сигнала в определенный момент времени и/или пространства; это определение отличается от использования этого термина в статистике , где он относится к набору таких значений. ^[A]

Сэмплер — это подсистема или операция, которая извлекает выборки из непрерывного сигнала . Теоретически идеальный сэмплер производит выборки, эквивалентные мгновенному значению непрерывного сигнала в желаемых точках.

Исходный сигнал можно восстановить из последовательности выборок вплоть до предела Найквиста , пропустив последовательность выборок через фильтр реконструкции .

Теория

Функции пространства, времени или любого другого измерения могут быть отобраны, и то же самое можно сделать в двух или более измерениях.

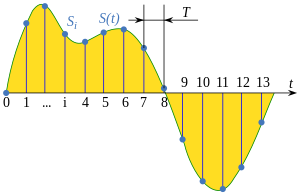
Для функций, которые изменяются со временем, пусть будет непрерывной функцией (или «сигналом»), подлежащей выборке, и пусть выборка выполняется путем измерения значения непрерывной функции каждые секунды, что называется интервалом выборки или периодом выборки . ^{[1] [2]} Тогда выборочная функция задается последовательностью: ${\displaystyle s(t)}$ ${\displaystyle T}$

${\displaystyle s(nT)}$, для целых значений . ${\displaystyle n}$

Частота дискретизации или частота дискретизации — это среднее число выборок, полученных за одну секунду, то есть единица измерения — выборки в секунду , иногда называемая герцем , например, 48 кГц — это 48 000 выборок в секунду . ${\displaystyle f_{s}}$ ${\displaystyle f_{s}=1/T}$

Восстановление непрерывной функции из выборок выполняется с помощью алгоритмов интерполяции. Формула интерполяции Уиттекера–Шеннона математически эквивалентна идеальному фильтру нижних частот , входом которого является последовательность дельта-функций Дирака , которые модулируются (умножаются) на значения выборки. Когда временной интервал между соседними выборками является константой , последовательность дельта-функций называется гребнем Дирака . Математически модулированный гребень Дирака эквивалентен произведению функции гребня на . Эту математическую абстракцию иногда называют импульсной выборкой . ^[3] ${\displaystyle (T)}$ ${\displaystyle s(t)}$

Большинство дискретизированных сигналов не просто сохраняются и реконструируются. Точность теоретической реконструкции является общепринятой мерой эффективности дискретизации. Эта точность снижается, когда содержит частотные компоненты, длина цикла (период) которых меньше 2 интервалов дискретизации (см. Наложение спектров ). Соответствующий предел частоты в циклах в секунду ( герц ) равен цикл/выборка × выборок/секунду = , известный как частота Найквиста дискретизатора. Таким образом, обычно является выходным сигналом фильтра нижних частот , функционально известного как фильтр сглаживания . Без фильтра сглаживания спектров частоты выше частоты Найквиста будут влиять на выборки таким образом, что процесс интерполяции будет неправильно истолкован. ^[4] ${\displaystyle s(t)}$ ${\displaystyle 0.5}$ ${\displaystyle f_{s}}$ ${\displaystyle f_{s}/2}$ ${\displaystyle s(t)}$

Практические соображения

На практике непрерывный сигнал дискретизируется с помощью аналого-цифрового преобразователя (АЦП), устройства с различными физическими ограничениями. Это приводит к отклонениям от теоретически идеальной реконструкции, которые в совокупности называются искажением .

Могут возникнуть различные типы искажений, в том числе:

• Алиасинг . Некоторое количество алиасинга неизбежно, поскольку только теоретические, бесконечно длинные функции не могут иметь частотного содержимого выше частоты Найквиста. Алиасинг можно сделать произвольно малым , используя достаточно большой порядок фильтра сглаживания.
• Ошибка апертуры возникает из-за того, что выборка получается как среднее по времени в пределах области выборки, а не просто равна значению сигнала в момент выборки. ^[5] В схеме выборки и хранения на основе конденсатора ошибки апертуры вносятся несколькими механизмами. Например, конденсатор не может мгновенно отслеживать входной сигнал, и конденсатор не может мгновенно изолироваться от входного сигнала.
• Джиттер или отклонение от точных временных интервалов выборки.
• Шум , включая шум теплового датчика, шум аналоговой схемы и т. д.
• Ошибка ограничения скорости нарастания , вызванная невозможностью входного значения АЦП изменяться достаточно быстро.
• Квантование как следствие конечной точности слов, представляющих преобразованные значения.
• Ошибка, вызванная другими нелинейными эффектами отображения входного напряжения в преобразованное выходное значение (в дополнение к эффектам квантования).

Хотя использование передискретизации может полностью устранить ошибку апертуры и наложение спектров, выведя их за пределы полосы пропускания, этот метод не может быть практически использован выше нескольких ГГц и может быть непозволительно дорогим на гораздо более низких частотах. Кроме того, хотя передискретизация может уменьшить ошибку квантования и нелинейность, она не может полностью их устранить. Следовательно, практические АЦП на звуковых частотах обычно не демонстрируют наложение спектров, ошибку апертуры и не ограничены ошибкой квантования. Вместо этого доминирует аналоговый шум. На радиочастотах и ​​микроволновых частотах, где передискретизация непрактична, а фильтры дороги, ошибка апертуры, ошибка квантования и наложение спектров могут быть существенными ограничениями.

Джиттер, шум и квантование часто анализируются путем моделирования их как случайных ошибок, добавленных к значениям выборки. Интеграция и эффекты удержания нулевого порядка могут быть проанализированы как форма фильтрации нижних частот . Нелинейности АЦП или ЦАП анализируются путем замены идеального линейного отображения функции на предлагаемую нелинейную функцию .

Приложения

Аудио сэмплирование

Цифровое аудио использует импульсно-кодовую модуляцию (ИКМ) и цифровые сигналы для воспроизведения звука. Это включает в себя аналого-цифровое преобразование (АЦП), цифро-аналоговое преобразование (ЦАП), хранение и передачу. По сути, система, обычно называемая цифровой, на самом деле является дискретным по времени и уровню аналогом предыдущего электрического аналога. Хотя современные системы могут быть довольно тонкими в своих методах, основная полезность цифровой системы заключается в способности хранить, извлекать и передавать сигналы без какой-либо потери качества.

Когда необходимо захватить аудио, охватывающее весь диапазон человеческого слуха 20–20 000 Гц ^[6], например, при записи музыки или многих типов акустических событий, аудиосигналы обычно дискретизируются на частоте 44,1 кГц ( CD ), 48 кГц, 88,2 кГц или 96 кГц. ^[7] Требование приблизительно двойной частоты является следствием теоремы Найквиста . Частоты дискретизации выше, чем примерно 50 кГц–60 кГц, не могут предоставить больше полезной информации для слушателей. По этой причине первые производители профессионального аудиооборудования выбирали частоты дискретизации в районе 40–50 кГц.

В отрасли наблюдается тенденция к частотам дискретизации, значительно превышающим основные требования: например, 96 кГц и даже 192 кГц ^[8]. Несмотря на то, что ультразвуковые частоты не слышны человеку, запись и микширование на более высоких частотах дискретизации эффективно устраняют искажения, которые могут быть вызваны фолдбэк-алиасингом . И наоборот, ультразвуковые звуки могут взаимодействовать с слышимой частью частотного спектра и модулировать ее ( интермодуляционные искажения ), ухудшая точность воспроизведения. ^[9] Одним из преимуществ более высоких частот дискретизации является то, что они могут смягчить требования к конструкции фильтра нижних частот для АЦП и ЦАП , но с современными дельта-сигма-преобразователями с избыточной дискретизацией это преимущество менее важно.

Audio Engineering Society рекомендует частоту дискретизации 48 кГц для большинства приложений, но признает 44,1 кГц для CD и других потребительских применений, 32 кГц для приложений, связанных с передачей, и 96 кГц для более высокой полосы пропускания или ослабленной фильтрации сглаживания . ^[10] И Lavry Engineering, и J. Robert Stuart утверждают, что идеальная частота дискретизации будет около 60 кГц, но поскольку это не стандартная частота, рекомендуют 88,2 или 96 кГц для целей записи. ^{[11] [12] [13] [14]}

Более полный список распространенных частот дискретизации звука:

Глубина цвета

Аудио обычно записывается с глубиной 8, 16 и 24 бит, что дает теоретическое максимальное отношение сигнал/шум квантования (SQNR) для чистой синусоиды приблизительно 49,93  дБ , 98,09 дБ и 122,17 дБ. ^[22] Аудио CD-качества использует 16-битные сэмплы. Тепловой шум ограничивает истинное количество бит, которые могут быть использованы при квантовании. Немногие аналоговые системы имеют отношение сигнал/шум (SNR), превышающее 120 дБ. Однако операции цифровой обработки сигнала могут иметь очень высокий динамический диапазон, поэтому обычно операции микширования и мастеринга выполняют с точностью 32 бита, а затем преобразуют в 16- или 24-бит для распространения.

Выборка речи

Речевые сигналы, т. е. сигналы, предназначенные для передачи только человеческой речи , обычно могут быть дискретизированы с гораздо более низкой частотой. Для большинства фонем почти вся энергия содержится в диапазоне 100 Гц – 4 кГц, что позволяет использовать частоту дискретизации 8 кГц. Это частота дискретизации, используемая почти всеми телефонными системами, которые используют спецификации дискретизации и квантования G.711 . ^{[ необходима цитата ]}

Видеовыборка

Телевидение стандартной четкости (SDTV) использует для видимой области изображения разрешение 720 на 480 пикселей (US NTSC 525 строк) или 720 на 576 пикселей (UK PAL 625 строк).

Телевидение высокой четкости (HDTV) использует форматы 720p (прогрессивный), 1080i (чересстрочный) и 1080p (прогрессивный, также известный как Full-HD).

В цифровом видео временная частота дискретизации определяется как частота кадров  — или, скорее, частота поля  — а не как условные пиксельные часы. Частота дискретизации изображения — это частота повторения периода интеграции сенсора. Поскольку период интеграции может быть значительно короче времени между повторениями, частота дискретизации может отличаться от обратной величины времени выборки:

• 50 Гц – видео PAL
• 60 / 1,001 Гц ~= 59,94 Гц – видео NTSC

Цифро-аналоговые преобразователи видео работают в мегагерцовом диапазоне (от ~3 МГц для низкокачественных композитных видеомасштабаторов в ранних игровых консолях до 250 МГц и более для выхода VGA с самым высоким разрешением).

Когда аналоговое видео преобразуется в цифровое видео , происходит другой процесс выборки, на этот раз с частотой пикселей, соответствующей пространственной частоте выборки вдоль строк сканирования . Обычная частота выборки пикселей составляет:

• 13,5 МГц — CCIR 601 , видео D1

Пространственная выборка в другом направлении определяется интервалом между строками сканирования в растре . Частоты выборки и разрешения в обоих пространственных направлениях могут быть измерены в единицах строк на высоту изображения.

Пространственное наложение высокочастотных компонентов яркости или цветности видео проявляется в виде муарового узора .

3D-выборка

Процесс объемного рендеринга использует 3D-сетку вокселей для создания 3D-рендеров срезов (томографических) данных. Предполагается, что 3D-сетка представляет собой непрерывную область трехмерного пространства. Объемный рендеринг распространен в медицинской визуализации, рентгеновской компьютерной томографии (КТ/КТ), магнитно-резонансной томографии (МРТ), позитронно-эмиссионной томографии (ПЭТ) — вот некоторые примеры. Он также используется для сейсмической томографии и других приложений.

Два верхних графика изображают преобразования Фурье двух различных функций, которые дают одинаковые результаты при дискретизации с определенной скоростью. Функция базовой полосы дискретизируется быстрее, чем ее скорость Найквиста, а функция полосы пропускания дискретизируется недостаточно, что фактически преобразует ее в базовую полосу. Нижние графики показывают, как идентичные спектральные результаты создаются псевдонимами процесса дискретизации.

Недостаточная выборка

Когда полосовой сигнал дискретизируется медленнее, чем его скорость Найквиста , выборки неотличимы от выборок низкочастотного псевдонима высокочастотного сигнала. Это часто делается намеренно таким образом, чтобы низкочастотный псевдоним удовлетворял критерию Найквиста , поскольку полосовой сигнал по-прежнему уникально представлен и восстанавливаем. Такая недостаточная выборка также известна как полосовая выборка , гармоническая выборка , выборка ПЧ и прямое преобразование ПЧ в цифровую форму. ^[23]

Передискретизация

Передискретизация используется в большинстве современных аналого-цифровых преобразователей для уменьшения искажений, вносимых практическими цифро-аналоговыми преобразователями , например, удержание нулевого порядка вместо идеализаций, таких как интерполяционная формула Уиттекера-Шеннона . ^[24]

Комплексная выборка

Комплексная выборка (или выборка I/Q ) — это одновременная выборка двух различных, но связанных форм сигналов, в результате чего получаются пары выборок, которые впоследствии обрабатываются как комплексные числа . ^[C] Когда одна форма сигнала, , является преобразованием Гильберта другой формы сигнала, , комплекснозначная функция, , называется аналитическим сигналом , преобразование Фурье которого равно нулю для всех отрицательных значений частоты. В этом случае скорость Найквиста для формы сигнала без частот ≥  B может быть уменьшена просто до B (комплексных выборок/сек), вместо (действительных выборок/сек). ^[D] Более очевидно, что эквивалентная форма сигнала основной полосы частот , , также имеет скорость Найквиста , поскольку все ее ненулевое частотное содержимое смещено в интервал . ${\displaystyle {\hat {s}}(t)}$ ${\displaystyle s(t)}$ ${\displaystyle s_{a}(t)\triangleq s(t)+i\cdot {\hat {s}}(t)}$ ${\displaystyle 2B}$ ${\displaystyle s_{a}(t)\cdot e^{-i2\pi {\frac {B}{2}}t}}$ ${\displaystyle B}$ ${\displaystyle [-B/2,B/2]}$

Хотя комплексные выборки могут быть получены, как описано выше, они также создаются путем манипулирования выборками действительной формы сигнала. Например, эквивалентная форма сигнала основной полосы может быть создана без явного вычисления , путем обработки последовательности продукта, , ^[E] через цифровой фильтр нижних частот, частота среза которого равна . ^[F] Вычисление только каждой второй выборки выходной последовательности снижает частоту выборки соразмерно уменьшенной частоте Найквиста. Результатом является половина комплексных выборок по сравнению с исходным числом действительных выборок. Никакая информация не теряется, и исходная форма сигнала может быть восстановлена, если необходимо. ${\displaystyle {\hat {s}}(t)}$ ${\displaystyle \left[s(nT)\cdot e^{-i2\pi {\frac {B}{2}}Tn}\right]}$ ${\displaystyle B/2}$ ${\displaystyle s(t)}$

Смотрите также

• Частоты кварцевого генератора
• Понижение частоты дискретизации
• Апсемплинг
• Многомерная выборка
• Синфазные и квадратурные компоненты и данные I/Q
• Преобразование частоты дискретизации
• Оцифровка
• Выборка и удержание
• Бета-кодер
• фактор Келла
• Скорость передачи данных
• Нормализованная частота

Примечания

1. Например, «количество выборок» в обработке сигналов примерно эквивалентно « размеру выборки » в статистике.
2. Существуют даже более высокие частоты дискретизации DSD, но преимущества от них, скорее всего, неощутимы, а размер таких файлов будет огромным.
3. Пары образцов также иногда рассматриваются как точки на диаграмме созвездия .
4. Когда комплексная частота дискретизации равна B , частотный компонент при 0,6  B , например, будет иметь псевдоним при −0,4  B , что однозначно из-за ограничения, что предварительно дискретизированный сигнал был аналитическим. Также см. Псевдонимизация § Комплексные синусоиды .
5. Когда s ( t ) дискретизируется на частоте Найквиста (1/ T = 2 B ), последовательность продуктов упрощается до ${\displaystyle \left[s(nT)\cdot (-i)^{n}\right].}$
6. Последовательность комплексных чисел свёртывается с импульсной характеристикой фильтра с действительными коэффициентами. Это эквивалентно раздельной фильтрации последовательностей действительных и мнимых частей и преобразованию комплексных пар на выходах.

Ссылки

1. Мартин Х. Вайк (1996). Communications Standard Dictionary. Springer. ISBN 0412083914.
2. Том Дж. Мойр (2022). Основы обработки сигналов и систем. Springer International Publishing AG. стр. 459. doi :10.1007/978-3-030-76947-5. ISBN 9783030769475.
3. Рао, Р. (2008). Сигналы и системы. Prentice-Hall Of India Pvt. Limited. ISBN 9788120338593.
4. CE Shannon , «Связь в присутствии шума», Proc. Institute of Radio Engineers , т. 37, № 1, стр. 10–21, январь 1949 г. Перепечатано как классическая статья в: Proc. IEEE, т. 86, № 2, (февраль 1998 г.) Архивировано 08.02.2010 на Wayback Machine
5. HO Johansson и C. Svensson, «Временное разрешение NMOS-выборочных переключателей», IEEE J. Solid-State Circuits Том: 33, Выпуск: 2, стр. 237–245, февраль 1998 г.
6. D'Ambrose, Christoper; Choudhary, Rizwan (2003). Elert, Glenn (ред.). «Диапазон частот человеческого слуха». The Physics Factbook . Получено 22.01.2022 .
7. Селф, Дуглас (2012). Объяснение аудиотехники. Тейлор и Фрэнсис США. стр. 200, 446. ISBN 978-0240812731.
8. "Digital Pro Sound" . Получено 8 января 2014 г.
9. Колетти, Джастин (4 февраля 2013 г.). «Наука о частотах дискретизации (когда выше — лучше, а когда нет)». Поверьте мне, я ученый . Получено 6 февраля 2013 г. во многих случаях мы можем слышать звук более высоких частот дискретизации не потому, что они более прозрачны, а потому, что они менее прозрачны. Они могут фактически вносить непреднамеренные искажения в слышимый спектр
10. AES5-2008: AES рекомендуемая практика для профессионального цифрового звука – Предпочтительные частоты дискретизации для приложений, использующих импульсно-кодовую модуляцию, Audio Engineering Society, 2008 , получено 18.01.2010
11. Lavry, Dan (3 мая 2012 г.). «Оптимальная частота дискретизации для качественного звука» (PDF) . Lavry Engineering Inc. Хотя 60 кГц было бы ближе к идеалу, учитывая существующие стандарты, 88,2 кГц и 96 кГц наиболее близки к оптимальной частоте дискретизации.
12. Lavry, Dan. "Оптимальная частота дискретизации для качественного звука". Gearslutz . Получено 10.11.2018 . Я пытаюсь учесть все уши, и есть сообщения о нескольких людях, которые действительно могут слышать немного выше 20 кГц. Я думаю, что 48 кГц — это довольно хороший компромисс, но 88,2 или 96 кГц дают некоторый дополнительный запас.
13. Lavry, Dan. "To mix at 96k or not?". Gearslutz . Получено 10.11.2018 . В настоящее время есть ряд хороших дизайнеров и специалистов по слуху, которые считают частоту дискретизации 60-70 кГц оптимальной для слуха. Она достаточно быстра, чтобы включить то, что мы слышим, но достаточно медленна, чтобы делать это довольно точно.
14. Стюарт, Дж. Роберт (1998). Кодирование высококачественного цифрового звука . CiteSeerX 10.1.1.501.6731 . И психоакустический анализ, и опыт говорят нам, что минимальный прямоугольный канал, необходимый для обеспечения прозрачности, использует линейную PCM с 18,2-битными выборками при 58 кГц. ... существуют веские аргументы в пользу сохранения целочисленных соотношений с существующими частотами дискретизации, что предполагает принятие 88,2 кГц или 96 кГц. 
15. «Cisco VoIP-телефоны, сетевое оборудование и аксессуары — поставка VoIP».
16. "Процедура восстановления – часть 1". Restoring78s.co.uk. Архивировано из оригинала 2009-09-14 . Получено 2011-01-18 . Для большинства записей частота дискретизации 22050 в стерео является адекватной. Исключением, вероятно, будут записи, сделанные во второй половине века, для которых может потребоваться частота дискретизации 44100.
17. "Zaxcom digital wireless transmitters". Zaxcom.com. Архивировано из оригинала 2011-02-09 . Получено 2011-01-18 .
18. "RME: Hammerfall DSP 9632". www.rme-audio.de . Получено 2018-12-18 . Поддерживаемые частоты дискретизации: Внутренние 32, 44.1, 48, 64, 88.2, 96, 176.4, 192 кГц.
19. "SX-S30DAB | Pioneer". www.pioneer-audiovisual.eu . Получено 2018-12-18 . Поддерживаемые частоты дискретизации: 44,1 кГц, 48 кГц, 64 кГц, 88,2 кГц, 96 кГц, 176,4 кГц, 192 кГц
20. Кристина Бахманн, Хайко Бишофф; Шютте, Бенджамин. "Настроить меню частоты дискретизации". Steinberg WaveLab Pro . Получено 18.12.2018 . Распространенные частоты дискретизации: 64 000 Гц
21. "M Track 2x2M Cubase Pro 9 не может изменить частоту дискретизации". M-Audio . Получено 2018-12-18 . [Скриншот Cubase]
22. «MT-001: Раскрытие тайны печально известной формулы «SNR=6,02N + 1,76 дБ» и почему это должно вас волновать» (PDF) .
23. Уолт Кестер (2003). Методы проектирования смешанных сигналов и DSP. Newnes. стр. 20. ISBN 978-0-7506-7611-3. Получено 8 января 2014 г.
24. Уильям Моррис Хартманн (1997). Сигналы, звук и ощущение. Springer. ISBN 1563962837.

Дальнейшее чтение

• Мэтт Фарр, Венцель Якоб и Грег Хамфрис, Физически обоснованный рендеринг: от теории к реализации, 3-е изд. , Morgan Kaufmann, ноябрь 2016 г. ISBN 978-0128006450 . Глава о сэмплировании (доступна онлайн) прекрасно написана с диаграммами, базовой теорией и примером кода. 

Внешние ссылки

• Журнал, посвященный теории выборочного контроля
• Данные I/Q для чайников — страница, на которой пытаются ответить на вопрос « Почему данные I/Q?»
• Дискретизация аналоговых сигналов – интерактивная презентация в веб-демонстрации в Институте телекоммуникаций Штутгартского университета