stringtranslate.com

5

5 ( пять ) — число , цифра и числовое значение . Это натуральное число , количественное числительное , следующее за 4 и предшествующее 6 , и является простым числом .

У людей и многих других животных на конечностях по 5 пальцев .

Математика

Первая пифагорова тройка

5 — простое число Ферма , показатель степени простого числа Мерсенна , а также число Фибоначчи . 5 — первое конгруэнтное число , а также длина гипотенузы наименьшего прямоугольного треугольника с целыми сторонами , входящего в наименьшую пифагорейскую тройку ( 3 , 4 , 5). [1]

5 — первое безопасное простое число [ 2] и первое хорошее простое число [ 3] . 11 образует первую пару сексуальных простых чисел с 5. [4] 5 — второе простое число Ферма из пяти известных простых чисел Ферма. [5] 5 также является первым из трех известных простых чисел Вильсона (5, 13, 563). [6]

Геометрия

Фигура с пятью сторонами называется пентагон . Пентагон — первый правильный многоугольник , который не замощает плоскость своими копиями. Это самая большая грань, которую может иметь любое из пяти правильных трехмерных правильных Платоновых тел .

Коника определяется с помощью пяти точек таким же образом, как для определения прямой нужны две точки . [7] Пентаграмма , или пятиконечная полиграмма , представляет собой звездчатый многоугольник, построенный путем соединения некоторых несмежных частей правильного пятиугольника в качестве самопересекающихся ребер . [8] Внутренняя геометрия пятиугольника и пентаграммы (представленная символом Шлефли {5/2} ) занимает видное место в мозаиках Пенроуза . Пентаграммы представляют собой грани внутри звездчатых многогранников Кеплера–Пуансо и звездчатых многогранников Шлефли–Гесса .

Существует пять правильных Платоновых тел: тетраэдр , куб , октаэдр , додекаэдр и икосаэдр . [ 9]

Хроматическое число плоскости — это минимальное количество цветов, необходимое для раскрашивания плоскости таким образом, чтобы ни одна пара точек на расстоянии 1 не имела одинаковый цвет. [ 10] Пять — это меньшее число, зависящее от хроматического числа плоскости, но это может зависеть от выбора аксиом теории множеств : [11]

Плоскость содержит в общей сложности пять решеток Браве , или массивов точек, определяемых дискретными операциями переноса . Однородные мозаики плоскости генерируются из комбинаций всего пяти правильных многоугольников. [12]

Геометрия более высокого измерения

Гипертетраэдр , или 5-ячейка, является 4- мерным аналогом тетраэдра . Он имеет пять вершин. Его ортографическая проекция гомоморфна группе K 5. [ 13] : стр.120 

Существует пять фундаментальных семейств точечных групп зеркальной симметрии в 4-мерном пространстве . Существует также 5 компактных гиперболических групп Коксетера , или 4-призм , ранга 5, каждая из которых генерирует однородные соты в гиперболическом 4-пространстве как перестановки колец диаграмм Коксетера. [14]

Четырехмерный 5-клеточный полихор является простейшим регулярным полихороном .

Алгебра

Наименьший нетривиальный магический квадрат

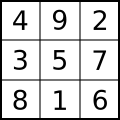
5 — значение центральной ячейки первого нетривиального нормального магического квадрата , называемого квадратом Луошу . Все целые числа можно выразить как сумму пяти ненулевых квадратов . [15] [16] Существует пять счетно бесконечных классов Рамсея перестановок . [ 17] : с.4  Предполагается , что 5 — единственное нечетное , неприкасаемое число ; если это так, то пять будет единственным нечетным простым числом, которое не является основанием аликвотного дерева. [18]

На этой диаграмме показаны субфакторные отношения двадцати шести спорадических групп ; пять групп Матье образуют простейший класс (окрашены в красный цвет).).

Предполагается, что каждое нечетное число больше пяти может быть выражено как сумма трех простых чисел; Хельфготт предоставил доказательство этого [19] (также известное как нечетная гипотеза Гольдбаха ), которое уже широко признано математиками, поскольку оно все еще проходит экспертную оценку . С другой стороны, каждое нечетное число больше единицы является суммой не более пяти простых чисел (как нижний предел). [20]

Нерешенная задача по математике :
Является ли 5 ​​единственным нечетным, неприкасаемым числом?
(еще нерешенные проблемы по математике)

Теория групп

В теории графов все графы с четырьмя или менее вершинами являются планарными , однако существует граф с пятью вершинами, который не является: K 5 , полный граф с пятью вершинами. По теореме Куратовского , конечный граф является планарным тогда и только тогда, когда он не содержит подграфа, который является подразделением , или K 3,3 , графа полезности . [21]

Существует пять комплексных исключительных алгебр Ли . Пять групп Матье составляют первое поколение в счастливом семействе спорадических групп . Это также первые пять спорадических групп, которые были описаны . [22] : стр.54  Централизатор элемента порядка 5 внутри наибольшей спорадической группы возникает из произведения спорадической группы Харады–Нортона и группы порядка 5. [23] [24]

Список основных расчетов

Эволюция арабской цифры

Эволюция современной западной цифры для обозначения цифры пять восходит к индийской системе цифр, где в некоторых ранних версиях цифра имела сходство с вариациями цифры четыре, а не с «5» (как она представлена ​​сегодня). Империи Кушана и Гупта на территории современной Индии имели между собой несколько форм, которые не имели никакого сходства с современной цифрой. Позже арабские традиции преобразовали цифру несколькими способами, создав формы, которые все еще были похожи на цифру четыре, со сходством с цифрой три; но все еще непохожи на современную пять. [25] Именно из этих цифр европейцы в конечном итоге придумали современную 5 (представленную, например, в трудах Дюрера).

В то время как в большинстве современных шрифтов форма символа цифры 5 имеет выносной элемент , в шрифтах с текстовыми цифрами глиф обычно имеет подстрочный элемент , как, например, в.

На семисегментном дисплее калькулятора и цифровых часов он представлен пятью сегментами в четырех последовательных поворотах сверху вниз, вращаясь сначала против часовой стрелки, затем по часовой стрелке и наоборот. Это одно из трех чисел, наряду с 4 и 6, где количество сегментов соответствует числу.

Другие поля

Астрономия

В системе двух тел имеется пять точек Лагранжа .

Биология

Обычно считается, что существует пять чувств (в общих чертах ); пять основных вкусов — сладкий , соленый , кислый , горький и умами . [26] Почти все земноводные, рептилии и млекопитающие, у которых есть пальцы рук или ног, имеют по пять пальцев на каждой конечности. [27] Пять — это число придатков у большинства морских звезд , которые демонстрируют пентамерию . [28]

Вычислительная техника

5 — это код ASCII символа запроса , который сокращенно обозначается как ENQ. [29]

Литература

Поэзия

Ямб — это стих с пятью повторяющимися стопами в строке; ямб — наиболее известная форма, используемая Уильямом Шекспиром . [30]

Музыка

Современная нотная запись использует нотный стан, состоящий из пяти горизонтальных линий. [31] Гамма с пятью нотами на октаву называется пентатонической . [32] Чистая квинта является наиболее консонантной гармонией и является основой для большинства западных систем настройки. [33] В гармониках пятый парциальный (или 4-й обертон ) основного тона имеет частотное отношение 5:1 к частоте этого основного тона. Это отношение соответствует интервалу в 2 октавы плюс чистая мажорная терция. Таким образом, интервал 5:4 является интервалом чистой терции. Аккорд мажорного трезвучия , сыгранный только интонацией (чаще всего в случае пения вокального ансамбля a cappella ), будет содержать такую ​​чистую мажорную терцию.

Пять — это наименьшее возможное число, которое может быть наивысшим числом тактового размера с асимметричным метром .

Религия

иудаизм

Книга Чисел — одна из пяти книг Торы ; остальные — книги Бытия , Исхода , Левита и Второзакония . Их все вместе называют Пятью Книгами Моисея , Пятикнижием ( по-гречески «пять контейнеров», имея в виду футляры для свитков, в которых хранились книги), или Хумашем ( חומש , по-еврейски «пятый»). [34] Хамса , древний символ в форме руки с четырьмя пальцами и одним большим пальцем, используется евреями в качестве защитного амулета ; этот же символ также очень популярен в арабской культуре, как известно , защищая от зависти и дурного глаза . [35]

христианство

В христианстве традиционно выделяют пять ран Иисуса Христа : раны от гвоздей на двух руках Христа, раны от гвоздей на двух ногах Христа и рана от копья Христа (соответственно на четырех конечностях тела и голове). [36]

ислам

Пять столпов ислама . [37] Пятиконечная простая звезда ☆ — одна из пяти, используемых в исламских плитках гирих . [38]

Мистика

Гностицизм

Число пять было важным символическим числом в манихействе , где небесные существа, концепции и другие существа часто объединялись в группы по пять.

Алхимия

Согласно древнегреческим философам, таким как Аристотель , вселенная состоит из пяти классических элементов : вода , земля , воздух , огонь и эфир . Эта концепция была позже принята средневековыми алхимиками и в последнее время практикующими неоязыческие религии, такие как Викка . Согласно индуистской космологии , во вселенной есть пять элементов : дхарти, агни, джал, вайю эвам акаш (земля, огонь , вода, воздух и космос соответственно). В восточноазиатской традиции есть пять элементов: вода , огонь , земля , дерево и металл . [39] Японские названия дней недели , со вторника по субботу , происходят от этих элементов через отождествление элементов с пятью планетами, видимыми невооруженным глазом . [40] Кроме того, традиционный японский календарь имеет пятидневный недельный цикл, который все еще можно наблюдать в печатных смешанных календарях, сочетающих западные, китайско-буддийские и японские названия для каждого дня недели. В традиционном китайском Усине также есть пять элементов . [41]

Квинтэссенция , что означает «пятый элемент», относится к неуловимому пятому элементу, который завершает основные четыре элемента (воду, огонь, воздух и землю) как их союз. [ 42] Пентаграмма , или пятиконечная звезда, имеет мистическое значение в различных системах верований, включая бахаи , христианство , масонство , сатанизм , даосизм , телему и викку .

Разные поля

Пятерки всех четырех мастей в игральных картах

Смотрите также

Примечания

  1. ^ Sloane, N. J. A. (ред.). "Последовательность A003273 (Конгруэнтные числа)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 01.06.2016 .
  2. ^ Sloane, N. J. A. (ред.). "Последовательность A005385 (Безопасные простые числа p: (p-1)/2 также являются простыми числами)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 14.02.2023 .
  3. ^ Sloane, N. J. A. (ред.). "Последовательность A028388 (хорошие простые числа)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 01.06.2016 .
  4. ^ Sloane, N. J. A. (ред.). "Последовательность A023201 (Простые числа p, такие, что p + 6 также является простым числом. (Меньшее из пары сексуальных простых чисел.))". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 14.01.2023 .
  5. ^ Sloane, N. J. A. (ред.). "Последовательность A019434 (простые числа Ферма)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 21 июля 2022 г.
  6. ^ Sloane, N. J. A. (ред.). "Последовательность A007540 (простые числа Уилсона: простые числа p, такие, что (p-1)! равно -1 (mod p^2).)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 06.09.2023 .
  7. ^ Диксон, AC (март 1908 г.). «Коническое сечение через пять данных точек». The Mathematical Gazette . 4 (70). The Mathematical Association: 228–230. doi :10.2307/3605147. JSTOR  3605147. S2CID  125356690.
  8. ^ Слоан, Н. Дж. А. (ред.). «Последовательность A307681 (Разница между числом сторон и числом диагоналей выпуклого n-угольника.)». Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.
  9. ↑ Брайан Банч, Королевство бесконечных чисел . Нью-Йорк: WH Freeman & Company (2000): 61
  10. ^ de Grey, Aubrey DNJ (2018). «Хроматическое число плоскости не менее 5». Geombinatorics . 28 : 5–18. arXiv : 1804.02385 . MR  3820926. S2CID  119273214.
  11. ^ Exoo, Geoffrey; Ismailescu, Dan (2020). «Хроматическое число плоскости не менее 5: новое доказательство». Дискретная и вычислительная геометрия . 64. Нью-Йорк, Нью-Йорк: Springer : 216–226. arXiv : 1805.00157 . doi : 10.1007/s00454-019-00058-1. MR  4110534. S2CID  119266055. Zbl  1445.05040.
  12. ^ Грюнбаум, Бранко ; Шепард, Джеффри (ноябрь 1977 г.). «Tilings by Regular Polygons» (PDF) . Mathematics Magazine . 50 (5). Taylor & Francis, Ltd.: 227–236. doi :10.2307/2689529. JSTOR  2689529. S2CID  123776612. Zbl  0385.51006.
  13. ^ HSM Coxeter (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Dover Publications, Inc. стр. 1–368. ISBN 978-0-486-61480-9.
  14. ^ МакМаллен, Питер ; Шульте, Эгон (2002). Абстрактные правильные многогранники . Энциклопедия математики и ее приложений. Т. 92. Кембридж: Cambridge University Press. С. 162–164. doi :10.1017/CBO9780511546686. ISBN 0-521-81496-0. MR  1965665. S2CID  115688843.
  15. ^ Нивен, Иван ; Цукерман, Герберт С.; Монтгомери, Хью Л. (1980). Введение в теорию чисел (5-е изд.). Нью-Йорк, Нью-Йорк: John Wiley . С. 144, 145. ISBN 978-0-19-853171-5.
  16. ^ Sloane, N. J. A. (ред.). "Последовательность A047701 (Все положительные числа, которые не являются суммой 5 ненулевых квадратов.)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 2023-09-20 .
    Только двенадцать целых чисел до 33 не могут быть выражены в виде суммы пяти ненулевых квадратов: {1, 2, 3, 4, 6, 7, 9, 10, 12, 15, 18, 33}, где 2, 3 и 7 — единственные такие простые числа без выражения.
  17. ^ Бёттхер, Джулия ; Фониок, Ян (2013). «Свойства Рамсея перестановок». Электронный журнал комбинаторики . 20 (1): P2. arXiv : 1103.5686v2 . doi : 10.37236/2978. S2CID  17184541. Zbl  1267.05284.
  18. ^ Померанс, Карл; Ян, Хи-Сун (14 июня 2012 г.). «О неприкасаемых числах и связанных с ними проблемах» (PDF) . math.dartmouth.edu . Дартмутский колледж : 1. S2CID  30344483.Классификация предметов по математике 2010 года. 11A25, 11Y70, 11Y16.
  19. ^ Хельфготт, Харальд Андрес (2014). «Тернарная проблема Гольдбаха» (PDF) . Ин Джанг, Сан Ён (ред.). Труды Сеульского международного конгресса математиков . Том 2. Сеул, Корея: Kyung Moon SA. стр. 391–418. ISBN 978-89-6105-805-6. OCLC  913564239.
  20. ^ Тао, Теренс (март 2014 г.). «Каждое нечетное число, большее 1, имеет представление в виде суммы не более пяти простых чисел» (PDF) . Mathematics of Computation . 83 (286): 997–1038. doi :10.1090/S0025-5718-2013-02733-0. MR  3143702. S2CID  2618958.
  21. ^ Бернстайн, Майкл (1978). «Теорема Куратовского-Понтрягина о планарных графах». Журнал комбинаторной теории . Серия B. 24 (2): 228–232. doi : 10.1016/0095-8956(78)90024-2 .
  22. ^ Роберт Л. Грисс-младший (1998). Двенадцать спорадических групп . Монографии Спрингера по математике. Берлин: Springer-Verlag. стр. 1−169. дои : 10.1007/978-3-662-03516-0. ISBN 978-3-540-62778-4. МР  1707296. S2CID  116914446. Збл  0908.20007.
  23. ^ Люкс, Клаус; Ноеске, Феликс; Рыба, Александр JE (2008). «5-модулярные характеры спорадической простой группы Харада–Нортона HN и ее группа автоморфизмов HN.2». Журнал алгебры . 319 (1). Амстердам: Elsevier : 320–335. doi : 10.1016/j.jalgebra.2007.03.046 . MR  2378074. S2CID  120706746. Zbl  1135.20007.
  24. ^ Уилсон, Роберт А. (2009). «Нечетные локальные подгруппы монстра». Журнал Австралийского математического общества (серия A) . 44 (1). Кембридж: Cambridge University Press : 12–13. doi : 10.1017/S1446788700031323 . MR  0914399. S2CID  123184319. Zbl  0636.20014.
  25. ^ Жорж Ифра, Всеобщая история чисел: от доисторических времен до изобретения компьютера , перевод Дэвида Беллоса и др. Лондон: The Harvill Press (1998): 394, рис. 24.65
  26. ^ Маркус, Жаклин Б. (2013-04-15). Кулинарное питание: наука и практика здоровой кулинарии. Academic Press. стр. 55. ISBN 978-0-12-391883-3. Существует пять основных вкусов: сладкий, соленый, кислый, горький и умами...
  27. ^ Кисия, SM (2010), Позвоночные: структуры и функции, Биологические системы позвоночных, CRC Press, стр. 106, ISBN 978-1-4398-4052-8, Типичная конечность четвероногих — это пентадактильная конечность (греч. penta, пять), имеющая пять пальцев. Четвероногие произошли от предка, имевшего конечности с пятью пальцами. ... Несмотря на то, что количество пальцев у разных позвоночных может отличаться от пяти, позвоночные развиваются из эмбриональной стадии с пятью пальцами.
  28. ^ Cinalli, G.; Maixner, WJ; Sainte-Rose, C. (2012-12-06). Детская гидроцефалия. Springer Science & Business Media. стр. 19. ISBN 978-88-470-2121-1. Считается, что пять придатков морской звезды гомологичны пяти человеческим почкам.
  29. ^ Позрикидис, Константин (2012-09-17). XML в научных вычислениях. CRC Press. стр. 209. ISBN 978-1-4665-1228-3. 5 5 005 ENQ (запрос)
  30. ^ Veith (Jr.), Gene Edward; Wilson, Douglas (2009). Omnibus IV: The Ancient World. Veritas Press. стр. 52. ISBN 978-1-932168-86-0. Наиболее распространенными ударно-слоговыми строками являются пятистопные ямбические строки (пятистопный ямб)
  31. ^ "STAVE | значение в Cambridge English Dictionary". dictionary.cambridge.org . Получено 2020-08-02 . пять строк и четыре пробела между ними, на которых написаны музыкальные ноты
  32. ^ Рикер, Рамон (1999-11-27). Пентатонические гаммы для джазовой импровизации. Alfred Music. стр. 2. ISBN 978-1-4574-9410-9. Пентатонические гаммы, используемые в джазе, представляют собой пятинотные гаммы.
  33. ^ Дэннели, Джон Фелтем (1825). Энциклопедия, или словарь музыки...: с более чем двумя сотнями гравированных примеров, все составлено из самых известных иностранных и английских авторитетов, перемежаемых критическими и пояснительными замечаниями. редактор и издатель. являются чистая кварта, чистая квинта и октава
  34. ^ Пелайя, Ариэла. «Иудаизм 101: Что такое Пять Книг Моисея?». Learn Religions . Получено 2020-08-03 .
  35. ^ Зеннер, Уолтер П. (1988-01-01). Настойчивость и гибкость: антропологические перспективы американского еврейского опыта. SUNY Press. стр. 284. ISBN 978-0-88706-748-8.
  36. ^ "КАТОЛИЧЕСКАЯ ЭНЦИКЛОПЕДИЯ: Пять священных ран". www.newadvent.org . Получено 2020-08-02 .
  37. ^ "PBS – Ислам: Империя веры – Вера – Пять столпов". www.pbs.org . Получено 2020-08-03 .
  38. ^ Сарханги, Реза (2012). «Взаимодействующие звездчатые многоугольники в персидской архитектуре: особый случай декаграммы в мозаичных узорах» (PDF) . Nexus Network Journal . 14 (2): 350. doi : 10.1007/s00004-012-0117-5 . S2CID  124558613.
  39. ^ Юн, Хонг-кей (2006). Культура фэншуй в Корее: исследование восточноазиатской геомантии. Lexington Books. стр. 59. ISBN 978-0-7391-1348-6. Первая категория — это Пять Агентов [Элементов], а именно: Вода, Огонь, Дерево, Металл и Земля.
  40. ^ Уолш, Лен (2008-11-15). Читайте японский сегодня: легкий способ выучить 400 практических кандзи. Tuttle Publishing. ISBN 978-1-4629-1592-7Японские названия дней недели взяты из названий семи основных символов природы .
  41. ^ Чэнь, Юань (2014). «Дискурс легитимации и теория пяти элементов в императорском Китае». Журнал исследований Сун-Юань . 44 (1): 325–364. doi :10.1353/sys.2014.0000. ISSN  2154-6665. S2CID  147099574.
  42. ^ Кронланд-Мартине, Ричард; Истад, Сёлви; Дженсен, Кристоффер (19 июля 2008 г.). Компьютерное моделирование и поиск музыки. Чувство звуков: 4-й международный симпозиум, CMMR 2007, Копенгаген, Дания, август 2007 г., Пересмотренные статьи. Спрингер. п. 502. ИСБН 978-3-540-85035-9. Платон и Аристотель постулировали пятое состояние материи, которое они называли «идеей» или «квинтэссенцией» (от «квинт», что означает «пятый»).
  43. ^ "Олимпийские кольца – символ олимпийского движения". Международный олимпийский комитет . 2020-06-23 . Получено 2020-08-02 .
  44. ^ Лапланте, Филип А. (2018-10-03). Полный словарь по электротехнике. CRC Press. стр. 562. ISBN 978-1-4200-3780-7. квинконс пять точек

Ссылки

Дальнейшее чтение

Внешние ссылки