
Алгебраическая геометрия — это раздел математики , который использует абстрактные алгебраические методы, в основном из коммутативной алгебры , для решения геометрических задач . Классически она изучает нули многомерных полиномов ; современный подход обобщает это в нескольких различных аспектах.
Основными объектами изучения алгебраической геометрии являются алгебраические многообразия , которые являются геометрическими проявлениями решений систем полиномиальных уравнений . Примерами наиболее изученных классов алгебраических многообразий являются прямые , окружности , параболы , эллипсы , гиперболы , кубические кривые , такие как эллиптические кривые , и четвертичные кривые, такие как лемнискаты и овалы Кассини . Это плоские алгебраические кривые . Точка плоскости лежит на алгебраической кривой, если ее координаты удовлетворяют заданному полиномиальному уравнению . Базовые вопросы включают изучение точек особого интереса, таких как особые точки , точки перегиба и бесконечно удаленные точки . Более сложные вопросы включают топологию кривой и взаимосвязь между кривыми, определяемыми различными уравнениями.
Алгебраическая геометрия занимает центральное место в современной математике и имеет многочисленные концептуальные связи с такими разнообразными областями, как комплексный анализ , топология и теория чисел . Как изучение систем полиномиальных уравнений с несколькими переменными, предмет алгебраической геометрии начинается с нахождения конкретных решений посредством решения уравнений , а затем переходит к пониманию внутренних свойств совокупности решений системы уравнений. Это понимание требует как концептуальной теории, так и вычислительной техники.
В XX веке алгебраическая геометрия разделилась на несколько подобластей.
Большая часть развития основного направления алгебраической геометрии в 20 веке происходила в рамках абстрактной алгебраической структуры, при этом все большее внимание уделялось «внутренним» свойствам алгебраических многообразий, не зависящим от какого-либо конкретного способа вложения многообразия в окружающее координатное пространство; это соответствует разработкам в топологии, дифференциальной и комплексной геометрии . Одним из ключевых достижений этой абстрактной алгебраической геометрии является теория схем Гротендика , которая позволяет использовать теорию пучков для изучения алгебраических многообразий способом, который очень похож на ее использование при изучении дифференциальных и аналитических многообразий . Это достигается путем расширения понятия точки: в классической алгебраической геометрии точка аффинного многообразия может быть идентифицирована, посредством Nullstellensatz Гильберта , с максимальным идеалом координатного кольца , в то время как точки соответствующей аффинной схемы являются всеми простыми идеалами этого кольца. Это означает, что точка такой схемы может быть либо обычной точкой, либо подмногообразием. Этот подход также позволяет объединить язык и инструменты классической алгебраической геометрии, в основном занимающейся комплексными точками, и алгебраической теории чисел. Доказательство Уайлсом давней гипотезы, называемой Великой теоремой Ферма, является примером силы этого подхода.
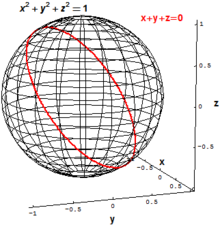
В классической алгебраической геометрии основными объектами интереса являются исчезающие множества наборов многочленов , то есть множество всех точек, которые одновременно удовлетворяют одному или нескольким полиномиальным уравнениям . Например, двумерная сфера радиуса 1 в трехмерном евклидовом пространстве R 3 может быть определена как множество всех точек с
«Наклонную» окружность в R 3 можно определить как множество всех точек , удовлетворяющих двум полиномиальным уравнениям
Сначала мы начнем с поля k . В классической алгебраической геометрии это поле всегда было комплексными числами C , но многие из тех же результатов верны, если мы предполагаем только, что k алгебраически замкнуто . Мы рассматриваем аффинное пространство размерности n над k , обозначаемое A n ( k ) (или проще A n , когда k ясно из контекста). Когда фиксируется система координат, можно отождествить A n ( k ) с k n . Цель не работы с k n состоит в том, чтобы подчеркнуть, что мы «забываем» структуру векторного пространства, которую несет k n .
Функция f : An → A 1 называется полиномиальной (или регулярной ), если ее можно записать в виде полинома, то есть если существует полином p в k [ x 1 , ... , x n ] такой, что f ( M ) = p ( t 1 ,..., t n ) для каждой точки M с координатами ( t 1 ,..., t n ) в A n . Свойство функции быть полиномиальной (или регулярной) не зависит от выбора системы координат в A n .
При выборе системы координат регулярные функции на аффинном n -пространстве можно отождествить с кольцом полиномиальных функций от n переменных над k . Таким образом, множество регулярных функций на A n представляет собой кольцо, которое обозначается k [ A n ].
Мы говорим, что многочлен обращается в нуль в точке, если его оценка в этой точке дает ноль. Пусть S — множество многочленов в k [ A n ]. Множество, исчезающее из S (или локус исчезновения или нулевое множество ) — это множество V ( S ) всех точек в A n , где каждый многочлен из S обращается в нуль. Символически,
Подмножество A n , которое равно V ( S ), для некоторого S , называется алгебраическим множеством . V означает разнообразие (конкретный тип алгебраического множества, который будет определен ниже).
Если задано подмножество U множества A n , можно ли восстановить множество многочленов, которые его порождают? Если U — любое подмножество множества A n , определим I ( U ) как множество всех многочленов, исчезающее множество которых содержит U . I обозначает идеал : если два многочлена f и g оба равны нулю на U , то f + g равен нулю на U , а если h — любой многочлен, то hf равен нулю на U , поэтому I ( U ) всегда является идеалом кольца многочленов k [ A n ].
Возникают два естественных вопроса:
Ответ на первый вопрос дается введением топологии Зарисского , топологии на A n , замкнутые множества которой являются алгебраическими множествами, и которая напрямую отражает алгебраическую структуру k [ A n ]. Тогда U = V ( I ( U )) тогда и только тогда, когда U является алгебраическим множеством или, что эквивалентно, замкнутым по Зарисскому множеством. Ответ на второй вопрос дается в Nullstellensatz Гильберта . В одной из своих форм он гласит, что I ( V ( S )) является радикалом идеала, порожденного S . На более абстрактном языке существует связь Галуа , порождающая два оператора замыкания ; их можно идентифицировать, и они, естественно, играют основную роль в теории; пример подробно рассматривается в связи Галуа.
По разным причинам мы не всегда хотим работать со всем идеалом , соответствующим алгебраическому множеству U. Теорема Гильберта о базисе подразумевает, что идеалы в k [ A n ] всегда конечно порождены.
Алгебраическое множество называется неприводимым, если его нельзя записать в виде объединения двух меньших алгебраических множеств. Любое алгебраическое множество является конечным объединением неприводимых алгебраических множеств, и это разложение единственно. Таким образом, его элементы называются неприводимыми компонентами алгебраического множества. Неприводимое алгебраическое множество также называется многообразием . Оказывается, что алгебраическое множество является многообразием тогда и только тогда, когда его можно определить как исчезающее множество простого идеала кольца многочленов.
Некоторые авторы не проводят четкого различия между алгебраическими множествами и многообразиями и при необходимости используют неприводимое многообразие для проведения различия.
Так же, как непрерывные функции являются естественными отображениями на топологических пространствах , а гладкие функции являются естественными отображениями на дифференцируемых многообразиях , существует естественный класс функций на алгебраическом множестве, называемых регулярными функциями или полиномиальными функциями . Регулярная функция на алгебраическом множестве V, содержащемся в A n, является ограничением на V регулярной функции на A n . Для алгебраического множества, определенного на поле комплексных чисел, регулярные функции являются гладкими и даже аналитическими .
Требование, чтобы регулярная функция всегда распространялась на окружающее ее пространство, может показаться неестественно ограничительным, но это очень похоже на ситуацию в нормальном топологическом пространстве , где теорема Титце о расширении гарантирует, что непрерывная функция на замкнутом подмножестве всегда расширяется на окружающее ее топологическое пространство.
Так же, как и регулярные функции на аффинном пространстве, регулярные функции на V образуют кольцо, которое мы обозначим через k [ V ]. Это кольцо называется координатным кольцом V .
Так как регулярные функции на V происходят от регулярных функций на A n , то между кольцами координат существует связь. В частности, если регулярная функция на V является ограничением двух функций f и g в k [ A n ], то f − g является полиномиальной функцией, которая равна нулю на V и, таким образом, принадлежит I ( V ). Таким образом, k [ V ] можно отождествить с k [ A n ]/ I ( V ).
Используя регулярные функции из аффинного многообразия в A 1 , мы можем определить регулярные отображения из одного аффинного многообразия в другое. Сначала мы определим регулярное отображение из многообразия в аффинное пространство: Пусть V будет многообразием, содержащимся в A n . Выберем m регулярных функций на V и назовем их f 1 , ..., f m . Мы определим регулярное отображение f из V в A m , положив f = ( f 1 , ..., f m ) . Другими словами, каждая f i определяет одну координату из диапазона f .
Если V ′ — многообразие, содержащееся в A m , мы говорим, что f — регулярное отображение из V в V ′, если область значений f содержится в V ′.
Определение регулярных отображений применимо также к алгебраическим множествам. Регулярные отображения также называются морфизмами , поскольку они объединяют все аффинные алгебраические множества в категорию , где объектами являются аффинные алгебраические множества, а морфизмами — регулярные отображения. Аффинные многообразия являются подкатегорией категории алгебраических множеств.
Если задано регулярное отображение g из V в V ′ и регулярная функция f от k [ V ′], то f ∘ g ∈ k [ V ] . Отображение f → f ∘ g является кольцевым гомоморфизмом из k [ V ′] в k [ V ]. Обратно, каждый кольцевой гомоморфизм из k [ V ′] в k [ V ] определяет регулярное отображение из V в V ′. Это определяет эквивалентность категорий между категорией алгебраических множеств и противоположной категорией конечно порожденных приведенных k -алгебр. Эта эквивалентность является одной из отправных точек теории схем .
В отличие от предыдущих разделов, этот раздел касается только многообразий, а не алгебраических множеств. С другой стороны, определения естественным образом распространяются на проективные многообразия (следующий раздел), поскольку аффинное многообразие и его проективное пополнение имеют одно и то же поле функций.
Если V — аффинное многообразие, его координатное кольцо является целостной областью и, таким образом, имеет поле дробей , которое обозначается k ( V ) и называется полем рациональных функций на V или, коротко, полем функций V . Его элементы — это ограничения на V рациональных функций над аффинным пространством, содержащим V . Область определения рациональной функции f — это не V , а дополнение подмногообразия (гиперповерхность), где знаменатель f равен нулю.
Как и в случае с регулярными отображениями, можно определить рациональное отображение из многообразия V в многообразие V '. Как и в случае с регулярными отображениями, рациональные отображения из V в V ' могут быть отождествлены с полевыми гомоморфизмами из k ( V ') в k ( V ).
Два аффинных многообразия бирационально эквивалентны , если между ними существуют две рациональные функции, обратные друг другу в областях, где обе определены. Эквивалентно, они бирационально эквивалентны, если их функциональные поля изоморфны.
Аффинное многообразие является рациональным многообразием, если оно бирационально эквивалентно аффинному пространству. Это означает, что многообразие допускает рациональную параметризацию , то есть параметризацию с рациональными функциями . Например, окружность уравнения является рациональной кривой, поскольку она имеет параметрическое уравнение
что также можно рассматривать как рациональную карту от линии к окружности.
Проблема разрешения особенностей состоит в том, чтобы узнать, является ли каждое алгебраическое многообразие бирационально эквивалентным многообразию, проективное пополнение которого невырождено (см. также гладкое пополнение ). Она была решена утвердительно в характеристике 0 Хейсуке Хиронакой в 1964 году и до сих пор не решена в конечной характеристике.

Так же, как формулы для корней многочленов второй, третьей и четвертой степени предполагают расширение действительных чисел до более алгебраически полного множества комплексных чисел, многие свойства алгебраических многообразий предполагают расширение аффинного пространства до более геометрически полного проективного пространства. В то время как комплексные числа получаются путем добавления числа i , корня многочлена x 2 + 1 , проективное пространство получается путем добавления соответствующих точек «на бесконечности», точек, где могут пересекаться параллельные прямые.
Чтобы увидеть, как это может произойти, рассмотрим многообразие V ( y − x 2 ) . Если мы его нарисуем, то получим параболу . Когда x стремится к положительной бесконечности, наклон прямой от начала координат до точки ( x , x 2 ) также стремится к положительной бесконечности. Когда x стремится к отрицательной бесконечности, наклон той же прямой стремится к отрицательной бесконечности.
Сравните это с многообразием V ( y − x 3 ). Это кубическая кривая . Когда x стремится к положительной бесконечности, наклон линии от начала координат до точки ( x , x 3 ) стремится к положительной бесконечности, как и раньше. Но в отличие от предыдущего, когда x стремится к отрицательной бесконечности, наклон той же линии также стремится к положительной бесконечности; полная противоположность параболе. Таким образом, поведение «на бесконечности» V ( y − x 3 ) отличается от поведения «на бесконечности» V ( y − x 2 ).
Рассмотрение проективного завершения двух кривых, которое является их продолжением «на бесконечности» в проективной плоскости , позволяет нам количественно оценить это различие: точка на бесконечности параболы является регулярной точкой , касательная к которой является линией на бесконечности , в то время как точка на бесконечности кубической кривой является точкой возврата . Кроме того, обе кривые рациональны, поскольку они параметризованы x , а теорема Римана-Роха подразумевает, что кубическая кривая должна иметь особенность, которая должна быть на бесконечности, поскольку все ее точки в аффинном пространстве являются регулярными.
Таким образом, многие свойства алгебраических многообразий, включая бирациональную эквивалентность и все топологические свойства, зависят от поведения «на бесконечности», и поэтому естественно изучать многообразия в проективном пространстве. Более того, введение проективных методов сделало многие теоремы в алгебраической геометрии проще и точнее: например, теорема Безу о числе точек пересечения между двумя многообразиями может быть сформулирована в своей наиболее точной форме только в проективном пространстве. По этим причинам проективное пространство играет фундаментальную роль в алгебраической геометрии.
В настоящее время проективное пространство P n размерности n обычно определяется как множество прямых, проходящих через точку, рассматриваемую как начало координат, в аффинном пространстве размерности n + 1 , или, что эквивалентно, множество векторных прямых в векторном пространстве размерности n + 1. Когда выбрана система координат в пространстве размерности n + 1 , все точки прямой имеют один и тот же набор координат с точностью до умножения на элемент k . Это определяет однородные координаты точки P n как последовательность из n + 1 элементов базового поля k , определенную с точностью до умножения на ненулевой элемент k (одинаковую для всей последовательности).
Многочлен от n + 1 переменной обращается в нуль во всех точках прямой, проходящей через начало координат, тогда и только тогда, когда он однороден . В этом случае говорят, что многочлен обращается в нуль в соответствующей точке P n . Это позволяет нам определить проективное алгебраическое множество в P n как множество V ( f 1 , ..., f k ) , где конечный набор однородных многочленов { f 1 , ..., f k } обращается в нуль. Как и для аффинных алгебраических множеств, существует биекция между проективными алгебраическими множествами и приведенными однородными идеалами , которые их определяют. Проективные многообразия — это проективные алгебраические множества, определяющий идеал которых является простым числом. Другими словами, проективное многообразие — это проективное алгебраическое множество, однородное координатное кольцо которого является областью целостности , причем проективное координатное кольцо определяется как фактор градуированного кольца или многочленов от n + 1 переменных по однородному (редуцированному) идеалу, определяющему многообразие. Каждое проективное алгебраическое множество может быть однозначно разложено в конечное объединение проективных многообразий.
Единственные регулярные функции, которые могут быть определены правильно на проективном многообразии, — это постоянные функции. Таким образом, это понятие не используется в проективных ситуациях. С другой стороны, поле рациональных функций или функциональное поле — полезное понятие, которое, подобно аффинному случаю, определяется как множество частных двух однородных элементов одинаковой степени в однородном координатном кольце.
Действительная алгебраическая геометрия — это изучение действительных алгебраических многообразий.
Тот факт, что поле действительных чисел является упорядоченным полем, не может быть проигнорирован в таком исследовании. Например, кривая уравнения является окружностью, если , но не имеет действительных точек, если . Действительная алгебраическая геометрия также исследует, в более широком смысле, полуалгебраические множества , которые являются решениями систем полиномиальных неравенств. Например, ни одна из ветвей гиперболы уравнения не является действительным алгебраическим многообразием. Однако ветвь в первом квадранте является полуалгебраическим множеством, определяемым и .
Одной из открытых проблем в реальной алгебраической геометрии является следующая часть шестнадцатой проблемы Гильберта : решить, какие соответствующие положения возможны для овалов неособой плоской кривой степени 8.
Зарождение вычислительной алгебраической геометрии можно отнести к встрече EUROSAM'79 (Международный симпозиум по символическим и алгебраическим манипуляциям), состоявшейся в Марселе , Франция, в июне 1979 года. На этой встрече
С тех пор большинство результатов в этой области связаны с одним или несколькими из этих элементов либо путем использования или улучшения одного из этих алгоритмов, либо путем нахождения алгоритмов, сложность которых просто экспоненциальна по числу переменных.
За последние несколько десятилетий была разработана математическая теория, дополняющая символические методы, называемая числовой алгебраической геометрией . Основным вычислительным методом является гомотопическое продолжение . Это поддерживает, например, модель вычислений с плавающей точкой для решения задач алгебраической геометрии.
Базис Грёбнера — это система генераторов полиномиального идеала , вычисление которой позволяет вывести многие свойства аффинного алгебраического многообразия, определяемого этим идеалом.
Дано идеал I, определяющий алгебраическое множество V :
Вычисления базиса Грёбнера не позволяют напрямую вычислять первичное разложение I или простые идеалы, определяющие неприводимые компоненты V , но большинство алгоритмов для этого включают вычисление базиса Грёбнера. Алгоритмы, которые не основаны на базисах Грёбнера, используют регулярные цепочки , но могут нуждаться в базисах Грёбнера в некоторых исключительных ситуациях.
Базисы Грёбнера считаются сложными для вычисления. Фактически, они могут содержать, в худшем случае, многочлены, степень которых дважды экспоненциальна по числу переменных, и количество многочленов, которое также дважды экспоненциально. Однако это только сложность в худшем случае, и ограничение сложности алгоритма Лазара 1979 года может часто применяться. Алгоритм Фожера F5 реализует эту сложность, так как его можно рассматривать как улучшение алгоритма Лазара 1979 года. Из этого следует, что лучшие реализации позволяют производить вычисления почти рутинно с алгебраическими множествами степени более 100. Это означает, что в настоящее время сложность вычисления базиса Грёбнера тесно связана с внутренней сложностью задачи.
CAD — это алгоритм, который был предложен в 1973 году Дж. Коллинзом для реализации с приемлемой сложностью теоремы Тарского–Зейденберга об исключении кванторов по действительным числам.
Эта теорема касается формул логики первого порядка , атомарные формулы которых являются полиномиальными равенствами или неравенствами между полиномами с действительными коэффициентами. Таким образом, эти формулы являются формулами, которые могут быть построены из атомарных формул с помощью логических операторов и (∧), или (∨), не (¬), для всех (∀) и существует (∃). Теорема Тарского утверждает, что из такой формулы можно вычислить эквивалентную формулу без квантификатора (∀, ∃).
Сложность САПР дважды экспоненциальна по числу переменных. Это означает, что САПР позволяет, в теории, решить любую задачу действительной алгебраической геометрии, которая может быть выражена такой формулой, то есть почти любую задачу, касающуюся явно заданных многообразий и полуалгебраических множеств.
В то время как вычисление базиса Грёбнера имеет двойную экспоненциальную сложность только в редких случаях, САПР имеет такую высокую сложность почти всегда. Это означает, что, если только большинство полиномов, появляющихся во входных данных, не являются линейными, он не может решать проблемы с более чем четырьмя переменными.
Начиная с 1973 года большая часть исследований по этой теме посвящена либо совершенствованию САПР, либо поиску альтернативных алгоритмов в особых случаях, представляющих общий интерес.
В качестве примера современного состояния дел, существуют эффективные алгоритмы для нахождения по крайней мере одной точки в каждом связанном компоненте полуалгебраического множества, и таким образом для проверки, является ли полуалгебраическое множество пустым. С другой стороны, CAD на практике все еще является лучшим алгоритмом для подсчета количества связанных компонентов.
Базовые общие алгоритмы вычислительной геометрии имеют двойную экспоненциальную сложность в худшем случае . Точнее, если d — максимальная степень входных полиномов, а n — число переменных, их сложность не превышает некоторой константы c , а для некоторых входных данных сложность не меньше другой константы c ′.
В течение последних 20 лет 20-го века были введены различные алгоритмы для решения конкретных подзадач с лучшей сложностью. Большинство этих алгоритмов имеют сложность . [1]
Среди этих алгоритмов, которые решают подзадачу задач, решаемых базисами Грёбнера, можно упомянуть проверку пустости аффинного многообразия и решение неоднородных полиномиальных систем, имеющих конечное число решений. Такие алгоритмы редко реализуются, поскольку для большинства записей алгоритмы Фожера F4 и F5 имеют лучшую практическую эффективность и, вероятно, аналогичную или лучшую сложность ( вероятно, потому что оценка сложности алгоритмов базиса Грёбнера для определенного класса записей является сложной задачей, которая была выполнена только в нескольких особых случаях).
Основные алгоритмы реальной алгебраической геометрии, которые решают задачу, решаемую САПР, связаны с топологией полуалгебраических множеств. Можно привести подсчет числа связанных компонентов , проверку того, находятся ли две точки в одних и тех же компонентах или вычисление стратификации Уитни реального алгебраического множества . Они имеют сложность , но константа, вовлеченная в обозначение O , настолько высока, что использование их для решения любой нетривиальной задачи, эффективно решаемой САПР, невозможно, даже если бы можно было использовать всю существующую вычислительную мощность в мире. Поэтому эти алгоритмы никогда не были реализованы, и это активная область исследований для поиска алгоритмов, которые имеют одновременно хорошую асимптотическую сложность и хорошую практическую эффективность.
Современные подходы к алгебраической геометрии переопределяют и эффективно расширяют круг базовых объектов на различных уровнях общности до схем, формальных схем , инд-схем , алгебраических пространств , алгебраических стеков и т. д. Необходимость в этом возникает уже из полезных идей в теории многообразий, например, формальные функции Зарисского могут быть учтены путем введения нильпотентных элементов в структурные кольца; рассмотрение пространств петель и дуг, построение факторов по групповым действиям и разработка формальных оснований для теории естественного пересечения и теории деформаций приводят к некоторым дальнейшим расширениям.
Наиболее примечательно, что в начале 1960-х годов алгебраические многообразия были включены в концепцию схемы Александра Гротендика . Их локальными объектами являются аффинные схемы или простые спектры, которые являются локально окольцованными пространствами, которые образуют категорию, которая антиэквивалентна категории коммутативных унитальных колец, расширяя двойственность между категорией аффинных алгебраических многообразий над полем k и категорией конечно порожденных приведенных k -алгебр. Склеивание осуществляется по топологии Зарисского; можно склеивать внутри категории локально окольцованных пространств, но также, используя вложение Йонеды, внутри более абстрактной категории предпучков множеств над категорией аффинных схем. Топология Зарисского в теоретико-множественном смысле затем заменяется топологией Гротендика . Гротендик ввел топологии Гротендика, имея в виду более экзотические, но геометрически более тонкие и чувствительные примеры, чем грубая топология Зарисского, а именно этальную топологию и две плоские топологии Гротендика: fppf и fpqc; в настоящее время стали известны некоторые другие примеры, включая топологию Нисневича . Пучки могут быть далее обобщены до стеков в смысле Гротендика, обычно с некоторыми дополнительными условиями представимости, приводящими к стекам Артина и, еще более тонким, стекам Делиня–Мамфорда , которые часто называют алгебраическими стеками.
Иногда другие алгебраические сайты заменяют категорию аффинных схем. Например, Николай Дуров ввел коммутативные алгебраические монады как обобщение локальных объектов в обобщенной алгебраической геометрии. В этой установке были реализованы версии тропической геометрии , абсолютной геометрии над полем из одного элемента и алгебраического аналога геометрии Аракелова .
Другое формальное обобщение возможно до универсальной алгебраической геометрии , в которой каждое многообразие алгебр имеет свою собственную алгебраическую геометрию. Термин многообразие алгебр не следует путать с алгебраическим многообразием .
Язык схем, стеков и обобщений оказался ценным способом работы с геометрическими концепциями и стал краеугольным камнем современной алгебраической геометрии.
Алгебраические стеки могут быть далее обобщены, и для многих практических вопросов, таких как теория деформаций и теория пересечений, это часто является наиболее естественным подходом. Можно расширить сайт Гротендика аффинных схем до более категориального сайта производных аффинных схем , заменив коммутативные кольца категорией бесконечности дифференциальных градуированных коммутативных алгебр или симплициальных коммутативных колец или подобной категории подходящим вариантом топологии Гротендика. Можно также заменить предпучки множеств предпучками симплициальных множеств (или группоидов бесконечности). Затем, при наличии подходящего гомотопического аппарата, можно разработать понятие производного стека как такого предпучка на категории бесконечности производных аффинных схем, который удовлетворяет определенной бесконечной категориальной версии аксиомы пучка (и, чтобы быть алгебраическим, индуктивно последовательности условий представимости). Категории модели Квиллена , категории Сигала и квазикатегории являются одними из наиболее часто используемых инструментов для формализации этого, приводя к производной алгебраической геометрии , введенной школой Карлоса Симпсона , включая Андре Хиршовица, Бертрана Тоена , Габриэль Веццози, Мишеля Вакье и других; и развитой далее Якобом Лурье , Бертраном Тоеном и Габриэль Веццози . Другая (некоммутативная) версия производной алгебраической геометрии, использующая категории A-бесконечности, была разработана с начала 1990-х годов Максимом Концевичем и последователями.
Некоторые из корней алгебраической геометрии восходят к работам эллинистических греков с V века до н. э. Например, Делосская задача заключалась в построении длины x так, чтобы куб со стороной x имел тот же объем, что и прямоугольный ящик a 2 b при данных сторонах a и b . Менехм ( ок. 350 г. до н. э. ) рассматривал задачу геометрически, пересекая пару плоских коник ay = x 2 и xy = ab . [2] В III веке до н. э. Архимед и Аполлоний систематически изучали дополнительные проблемы конических сечений с использованием координат. [2] [3] Аполлоний в «Кониках» далее развил метод, который настолько похож на аналитическую геометрию, что его работа, как иногда полагают, предвосхитила работу Декарта примерно на 1800 лет. [4] Его применение опорных линий, диаметра и касательной по сути ничем не отличается от нашего современного использования системы координат, где расстояния, измеренные вдоль диаметра от точки касания, являются абсциссами, а отрезки, параллельные касательной и отсекаемые между осью и кривой, являются ординатами. Он далее разработал соотношения между абсциссами и соответствующими координатами, используя геометрические методы, такие как использование парабол и кривых. [5] [6] [7] Средневековые математики, включая Омара Хайяма , Леонардо Пизанского , Герсонида и Николая Орезма в средневековый период , [8] решали некоторые кубические и квадратные уравнения чисто алгебраическими средствами, а затем интерпретировали результаты геометрически. Персидский математик Омар Хайям (родился в 1048 г. н. э.) считал, что существует связь между арифметикой , алгеброй и геометрией . [9] [10] [11] Это подверглось критике со стороны Джеффри Оукса, который утверждал, что изучение кривых с помощью уравнений началось с Декарта в семнадцатом веке. [12]
Подобные методы применения геометрических построений к алгебраическим задачам были также приняты рядом математиков эпохи Возрождения, таких как Джероламо Кардано и Никколо Фонтана «Тарталья», в их исследованиях кубического уравнения. Геометрический подход к задачам построения, а не алгебраический, был одобрен большинством математиков 16-го и 17-го веков, в частности Блезом Паскалем , который выступал против использования алгебраических и аналитических методов в геометрии. [13] Французские математики Франциск Виета , а позднее Рене Декарт и Пьер де Ферма произвели революцию в традиционном способе мышления о задачах построения посредством введения координатной геометрии . Они интересовались в первую очередь свойствами алгебраических кривых , такими как те, которые определяются диофантовыми уравнениями (в случае Ферма), и алгебраической переформулировкой классических греческих работ о конических и кубических сечениях (в случае Декарта).
В тот же период Блез Паскаль и Жерар Дезарг подошли к геометрии с другой точки зрения, разработав синтетические понятия проективной геометрии . Паскаль и Дезарг также изучали кривые, но с чисто геометрической точки зрения: аналог греческой линейки и конструкции циркуля . В конечном итоге, аналитическая геометрия Декарта и Ферма победила, поскольку она снабдила математиков 18-го века конкретными количественными инструментами, необходимыми для изучения физических проблем с использованием нового исчисления Ньютона и Лейбница . Однако к концу 18-го века большая часть алгебраического характера координатной геометрии была включена в исчисление бесконечно малых Лагранжа и Эйлера .
Потребовалось одновременное развитие неевклидовой геометрии и абелевых интегралов в 19 веке , чтобы вернуть старые алгебраические идеи в геометрическую лоно. Первое из этих новых разработок было подхвачено Эдмоном Лагерром и Артуром Кэли , которые попытались выяснить обобщенные метрические свойства проективного пространства. Кэли ввел идею однородных полиномиальных форм , и, более конкретно, квадратичных форм , на проективном пространстве. Впоследствии Феликс Клейн изучал проективную геометрию (наряду с другими типами геометрии) с точки зрения того, что геометрия на пространстве закодирована в определенном классе преобразований на пространстве. К концу 19 века проективные геометры изучали более общие виды преобразований на фигурах в проективном пространстве. Вместо проективных линейных преобразований, которые обычно рассматривались как дающие фундаментальную клейновскую геометрию на проективном пространстве, они также занимались бирациональными преобразованиями более высокой степени . Это более слабое понятие конгруэнтности позже привело членов итальянской школы алгебраической геометрии XX века к классификации алгебраических поверхностей с точностью до бирационального изоморфизма .
Второе направление исследований начала XIX века — абелевы интегралы — привело Бернхарда Римана к разработке римановых поверхностей .
В тот же период началась алгебраизация алгебраической геометрии через коммутативную алгебру . Выдающимися результатами в этом направлении являются теорема о базисе Гильберта и Nullstellensatz Гильберта , которые являются основой связи между алгебраической геометрией и коммутативной алгеброй, и многомерный результант Маколея , который является основой теории исключения . Вероятно, из-за размера вычислений, которые подразумеваются многомерными результантами, теория исключения была забыта в середине 20-го века, пока она не была обновлена теорией особенностей и вычислительной алгебраической геометрией. [a]
BL van der Waerden , Oscar Zariski и André Weil разработали основу алгебраической геометрии на основе современной коммутативной алгебры , включая теорию оценок и теорию идеалов . Одной из целей было дать строгую основу для доказательства результатов итальянской школы алгебраической геометрии . В частности, эта школа систематически использовала понятие общей точки без какого-либо точного определения, которое было впервые дано этими авторами в 1930-х годах.
В 1950-х и 1960-х годах Жан-Пьер Серр и Александр Гротендик переработали основы, используя теорию пучков . Позднее, примерно с 1960 года, и в значительной степени под руководством Гротендика, была разработана идея схем в сочетании с очень тонким аппаратом гомологических методов . После десятилетия быстрого развития область стабилизировалась в 1970-х годах, и были сделаны новые приложения, как к теории чисел, так и к более классическим геометрическим вопросам об алгебраических многообразиях, особенностях , модулях и формальных модулях .
Важным классом многообразий, нелегко понять непосредственно из их определяющих уравнений, являются абелевы многообразия , которые являются проективными многообразиями, точки которых образуют абелеву группу . Прототипическими примерами являются эллиптические кривые , которые имеют богатую теорию. Они сыграли важную роль в доказательстве Великой теоремы Ферма и также используются в криптографии эллиптических кривых .
Параллельно с абстрактным направлением алгебраической геометрии, которое занимается общими утверждениями о многообразиях, также были разработаны методы эффективного вычисления с конкретно заданными многообразиями, что привело к появлению новой области вычислительной алгебраической геометрии. Одним из основополагающих методов этой области является теория базисов Грёбнера , введенная Бруно Бухбергером в 1965 году. Другим основополагающим методом, более специально посвященным действительной алгебраической геометрии, является цилиндрическое алгебраическое разложение , введенное Джорджем Э. Коллинзом в 1973 году.
См. также: производная алгебраическая геометрия .
Аналитическое многообразие над полем действительных или комплексных чисел определяется локально как множество общих решений нескольких уравнений, включающих аналитические функции . Оно аналогично понятию алгебраического многообразия в том, что оно несет структурный пучок аналитических функций вместо регулярных функций. Любое комплексное многообразие является комплексным аналитическим многообразием. Поскольку аналитические многообразия могут иметь особые точки , не все комплексные аналитические многообразия являются многообразиями. Над неархимедовым полем аналитическая геометрия изучается с помощью жестких аналитических пространств .
Современная аналитическая геометрия над полем комплексных чисел тесно связана с комплексной алгебраической геометрией, как показал Жан-Пьер Серр в своей статье GAGA , [14] название которой по-французски означает Алгебраическая геометрия и аналитическая геометрия . Результаты GAGA над полем комплексных чисел могут быть распространены на жесткие аналитические пространства над неархимедовыми полями. [15]
Алгебраическая геометрия теперь находит применение в статистике , [16] теории управления , [17] [18] робототехнике , [19] кодах с исправлением ошибок , [20] филогенетике [21] и геометрическом моделировании . [22] Также есть связи с теорией струн , [23] теорией игр , [24] сопоставлением графов , [25] солитонами [26] и целочисленным программированием . [27]
Сам Хайям, по-видимому, был первым, кто задумал общую теорию кубических уравнений.