Огюстен-Жан Френель

Огюстен Жан Френель ^{[Примечание 1]} (10 мая 1788 г. – 14 июля 1827 г.) был французским инженером-строителем и физиком , чьи исследования в области оптики привели к почти единогласному принятию волновой теории света , исключая любые остатки корпускулярной теории Ньютона , с конца 1830-х годов ^[3] до конца 19 века. Он, возможно, более известен тем, что изобрел катадиоптрическую (отражательную/преломляющую) линзу Френеля и стал пионером в использовании «ступенчатых» линз для увеличения видимости маяков , что спасло бесчисленное количество жизней в море. Более простая диоптрическая (чисто преломляющая) ступенчатая линза, впервые предложенная графом Бюффоном ^[4] и независимо переизобретенная Френелем, используется в экранных лупах и в конденсорных линзах для проекторов верхнего света .

Выражая принцип вторичных волн Гюйгенса и принцип интерференции Юнга в количественных терминах и предполагая, что простые цвета состоят из синусоидальных волн, Френель дал первое удовлетворительное объяснение дифракции на прямых краях, включая первое удовлетворительное объяснение прямолинейного распространения на основе волн. ^[5] Частью его аргументации было доказательство того, что сложение синусоидальных функций одинаковой частоты, но разных фаз аналогично сложению сил с разными направлениями. Далее предполагая, что световые волны являются чисто поперечными , Френель объяснил природу поляризации , механизм хроматической поляризации и коэффициенты пропускания и отражения на границе раздела двух прозрачных изотропных сред. Затем, обобщая соотношение направление-скорость-поляризация для кальцита , он учёл направления и поляризации преломлённых лучей в двупреломляющих кристаллах двуосного класса (тех, для которых вторичные волновые фронты Гюйгенса не являются осесимметричными ). Период между первой публикацией его гипотезы чисто поперечных волн и представлением его первого правильного решения двухосной задачи составил менее года.

Позже он ввел термины линейная поляризация , круговая поляризация и эллиптическая поляризация , объяснил, как оптическое вращение можно понимать как разницу в скоростях распространения для двух направлений круговой поляризации, и (позволяя коэффициенту отражения быть комплексным ) объяснил изменение поляризации из-за полного внутреннего отражения , как это используется в ромбе Френеля . Защитники устоявшейся корпускулярной теории не могли сравниться с его количественными объяснениями стольких явлений на столь немногих предположениях.

Френель всю жизнь боролся с туберкулезом , от которого он скончался в возрасте 39 лет. Хотя он не стал публичной знаменитостью при жизни, он прожил достаточно долго, чтобы получить должное признание от своих коллег, включая (на смертном одре) медаль Румфорда Лондонского королевского общества , и его имя повсеместно встречается в современной терминологии оптики и волн. После того, как волновая теория света была включена в электромагнитную теорию Максвелла в 1860-х годах, некоторое внимание было отвлечено от величины вклада Френеля. В период между объединением физической оптики Френелем и более широким объединением Максвелла современный авторитет, Хамфри Ллойд , описал теорию поперечных волн Френеля как «самую благородную ткань, которая когда-либо украшала область физической науки, за исключением только системы Вселенной Ньютона». ^[6]

Ранний период жизни

Семья

Огюстен-Жан Френель (также известный как Огюстен Жан или просто Огюстен), родившийся в Брольи, Нормандия , 10 мая 1788 года, был вторым из четырёх сыновей архитектора Жака Френеля ^[11] и его жены Огюстин, урождённой Мериме. ^[12] Семья переезжала дважды — в 1789/90 году в Шербур [ ^13] и в 1794 году ^[14] в родной город Жака Матьё , где Огюстин проведёт 25 лет вдовой ^[15] , пережив двух своих сыновей.

Первый сын, Луи, был принят в Политехническую школу , стал лейтенантом артиллерии и погиб в бою в Хаке , Испания. ^[12] Третий, Леонор, ^[11] последовал за Огюстеном в гражданское строительство , стал его преемником на посту секретаря Комиссии по маякам ^[16] и помогал редактировать его собрание сочинений. ^[17] Четвертый, Фюльжанс Френель , стал лингвистом, дипломатом и востоковедом и иногда помогал Огюстену в переговорах. ^[18]^[19] Фюльжанс умер в Багдаде в 1855 году, возглавив миссию по исследованию Вавилона. ^[19]

Младший брат мадам Френель, Жан Франсуа «Леонор» Мериме ^[12], отец писателя Проспера Мериме , был художником , обратившим свое внимание на химию живописи. Он стал постоянным секретарем Школы изящных искусств и (до 1814 года) профессором Политехнической школы ^[20] и был первоначальной точкой контакта между Огюстеном и ведущими оптическими физиками того времени (см. ниже) .

Образование

Братья Френель изначально обучались на дому матерью. Болезненный Огюстен считался медлительным, не склонным к запоминанию; ^[21] но популярная история о том, что он едва ли начал читать до восьми лет, оспаривается. ^[22] В возрасте девяти или десяти лет он ничем не выделялся, за исключением своей способности превращать ветки деревьев в игрушечные луки и ружья, которые работали слишком хорошо, заслужив себе прозвище l'homme de génie (гениальный человек) от своих сообщников и дружное преследование со стороны старших. ^[23]

В 1801 году Огюстен был отправлен в École Centrale в Кане , в качестве компании Луи. Но Огюстен улучшил свои показатели: в конце 1804 года он был принят в École Polytechnique, заняв 17-е место на вступительном экзамене. ^[24]^[25] Поскольку подробные записи École Polytechnique начинаются с 1808 года, мы мало что знаем о времени, проведенном там Огюстеном, за исключением того, что он завел мало друзей, если вообще завел, и — несмотря на продолжающееся плохое здоровье — преуспел в рисовании и геометрии: ^[26] на первом году обучения он получил приз за решение геометрической задачи, поставленной Адрианом-Мари Лежандром . ^[27] Окончив его в 1806 году, он поступил в École Nationale des Ponts et Chaussées (Национальную школу мостов и дорог, также известную как "ENPC" или "École des Ponts"), которую окончил в 1809 году, поступив на службу в Corps des Ponts et Chaussées в качестве ingénieur ordinaire aspirant (ординарного инженера-стажера). Прямо или косвенно он оставался на службе в "Corps des Ponts" до конца своей жизни. ^[28]

Религиозное формирование

Родители Френеля были католиками секты янсенистов , для которых был характерен крайний августинский взгляд на первородный грех . Религия занимала первое место в домашнем обучении мальчиков. В 1802 году его мать сказала:

Я молю Бога, чтобы Он дал моему сыну благодать использовать великие таланты, которые он получил, для его собственной выгоды и для Бога всех. Многое будет спрошено с того, кому много дано, и больше всего будет взыскано с того, кто получил больше всего. ^[29]

Августин оставался янсенистом. ^[30] Он считал свои интеллектуальные таланты дарами Бога и считал своим долгом использовать их на благо других. ^[31] По словам его коллеги-инженера Альфонса Дюло, который помогал ему ухаживать за ним во время его последней болезни, Френель рассматривал изучение природы как часть изучения силы и благости Бога. Он ставил добродетель выше науки и гения. В свои последние дни он молился о «силе души», не только против смерти, но и против «прерывания открытий… из которых он надеялся извлечь полезное применение». ^[32]

Янсенизм считается еретическим в Римско-католической церкви, и Грэттан-Гиннесс предполагает, что именно поэтому Френель так и не получил постоянную должность преподавателя; ^[33] его единственное назначение на должность преподавателя было в Athénée зимой 1819–1820 годов. ^[34]^[35] Статья о Френеле в Католической энциклопедии не упоминает его янсенизм, но описывает его как «глубоко религиозного человека, отличавшегося острым чувством долга». ^[34]

Инженерные задания

Первоначально Френель был направлен в западный департамент Вандея . Там, в 1811 году, он предвосхитил то, что стало известно как процесс Сольве для производства кальцинированной соды , за исключением того, что рециркуляция аммиака не рассматривалась. ^[36] Это различие может объяснить, почему ведущие химики, узнавшие о его открытии от его дяди Леонора, в конечном итоге посчитали его неэкономичным. ^[37]

Около 1812 года Френель был отправлен в Нион , в южном департаменте Дром , для оказания помощи в строительстве имперской дороги, которая должна была соединить Испанию и Италию. ^[14] Именно в Нионе мы имеем первое свидетельство его интереса к оптике. 15 мая 1814 года, когда работа была вялой из-за поражения Наполеона, [ ^38] Френель написал « PS » своему брату Леонору, в котором, в частности, говорилось:

Я также хотел бы иметь статьи, которые могли бы рассказать мне об открытиях французских физиков в области поляризации света. Я видел в Moniteur несколько месяцев назад, что Биот прочитал Институту очень интересный мемуар о поляризации света . Хотя я и ломаю голову, я не могу догадаться, что это такое. ^[39]

Еще 28 декабря он все еще ждал информации, но к 10 февраля 1815 года он получил мемуары Биота. ^[40] ( Институт Франции взял на себя функции Французской академии наук и других академий в 1795 году. В 1816 году Академия наук вернула себе свое название и автономию, но осталась частью института. ^[41] )

В марте 1815 года, восприняв возвращение Наполеона с Эльбы как «нападение на цивилизацию», ^[42] Френель уехал без разрешения, поспешил в Тулузу и предложил свои услуги роялистскому сопротивлению, но вскоре оказался в списке больных. Вернувшись в Нион с поражением, он подвергся угрозам и его окна были разбиты. Во время Ста дней он был отстранен, который ему в конечном итоге разрешили провести в доме его матери в Матье. Там он использовал свой вынужденный досуг, чтобы начать свои оптические эксперименты. ^[43]

Вклад в физическую оптику

Исторический контекст: от Ньютона до Биота

Оценить реконструкцию физической оптики Френелем может помочь обзор фрагментированного состояния, в котором он нашел предмет. В этом подразделе оптические явления, которые не были объяснены или объяснения которых были оспорены, выделены жирным шрифтом .

Корпускулярная теория света , одобренная Исааком Ньютоном и принятая почти всеми учениками Френеля, легко объясняла прямолинейное распространение : корпускулы, очевидно, двигались очень быстро, так что их пути были почти прямыми. Волновая теория , разработанная Христианом Гюйгенсом в его «Трактате о свете» (1690), объясняла прямолинейное распространение, предполагая, что каждая точка, пересекаемая бегущим волновым фронтом, становится источником вторичного волнового фронта. Учитывая начальное положение бегущего волнового фронта, любое более позднее положение (согласно Гюйгенсу) было общей касательной поверхностью ( огибающей ) вторичных волновых фронтов, испускаемых из более раннего положения. ^[44] Поскольку протяженность общей касательной была ограничена протяженностью начального волнового фронта, повторное применение конструкции Гюйгенса к плоскому волновому фронту ограниченной протяженности (в однородной среде) давало прямой параллельный луч. Хотя эта конструкция действительно предсказывала прямолинейное распространение, ее было трудно согласовать с общепринятым наблюдением, что волновые фронты на поверхности воды могут огибать препятствия, и с аналогичным поведением звуковых волн, что заставило Ньютона до конца своей жизни утверждать, что если бы свет состоял из волн, он бы «изогнутся и распространился во все стороны» в тени. ^[45]

Теория Гюйгенса аккуратно объясняла закон обычного отражения и закон обычного преломления («закон Снеллиуса»), при условии, что вторичные волны распространяются медленнее в более плотных средах (с более высоким показателем преломления ). ^[46] Корпускулярная теория с гипотезой о том, что корпускулы подвергаются воздействию сил, действующих перпендикулярно поверхностям, объясняла те же законы одинаково хорошо, ^[47] хотя и с предположением, что свет распространяется быстрее в более плотных средах; это предположение было неверным, но его нельзя было напрямую опровергнуть с помощью технологий времен Ньютона или даже времен Френеля (см. измерения скорости света Фуко ) .

Аналогичным образом неубедительной была звездная аберрация — то есть кажущееся изменение положения звезды из-за скорости Земли поперек луча зрения (не путать со звездным параллаксом , который возникает из-за смещения Земли поперек луча зрения). Определенная Джеймсом Брэдли в 1728 году, звездная аберрация широко воспринималась как подтверждение корпускулярной теории. Но она была в равной степени совместима с волновой теорией, как отметил Эйлер в 1746 году — молчаливо предполагая, что эфир (предполагаемая среда, несущая волны) вблизи Земли не был возмущен движением Земли. ^[48]

Выдающейся силой теории Гюйгенса было его объяснение двойного лучепреломления (двойного лучепреломления) « исландского кристалла » (прозрачного кальцита ), исходя из предположения, что вторичные волны являются сферическими для обычного преломления (которое удовлетворяет закону Снеллиуса) и сфероидальными для необыкновенного преломления (которое не удовлетворяет). ^[49] В общем, построение общей касательной Гюйгенса подразумевает, что лучи являются путями наименьшего времени между последовательными положениями волнового фронта, в соответствии с принципом Ферма . ^[50]^[51] В особом случае изотропных сред вторичные волновые фронты должны быть сферическими, и построение Гюйгенса тогда подразумевает, что лучи перпендикулярны волновому фронту; действительно, закон обычного преломления может быть отдельно выведен из этой предпосылки, как это сделал Игнас-Гастон Парди до Гюйгенса. ^[52]

Хотя Ньютон отверг волновую теорию, он заметил ее потенциал для объяснения цветов, включая цвета « тонких пластин » (например, « колец Ньютона » и цвета небесного света, отраженного в мыльных пузырях), исходя из предположения, что свет состоит из периодических волн с самыми низкими частотами (самыми длинными длинами волн ) на красном конце спектра и самыми высокими частотами (самыми короткими длинами волн) на фиолетовом конце. В 1672 году он опубликовал весомый намек на этот эффект, ^[53]^[54]^{: 5088–5089,} но современные сторонники волновой теории не смогли действовать в соответствии с ним: Роберт Гук рассматривал свет как периодическую последовательность импульсов, но не использовал частоту в качестве критерия цвета, ^[55] в то время как Гюйгенс рассматривал волны как отдельные импульсы без какой-либо периодичности; ^[56] и Пардис умер молодым в 1673 году. Сам Ньютон пытался объяснить цвета тонких пластин с помощью корпускулярной теории, предполагая, что его корпускулы обладают волнообразным свойством чередования «припадков легкой передачи» и «припадков легкого отражения», ^[57] расстояние между подобными «припадками» зависит от цвета и среды ^[58] и, что неловко, от угла преломления или отражения в эту среду. ^[59]^[60]^{: 1144} Еще более неловко то, что эта теория требовала, чтобы тонкие пластины отражали только на задней поверхности, хотя толстые пластины явно отражали также и на передней поверхности. ^[61] Только в 1801 году Томас Янг в Бейкерианской лекции того года процитировал намек Ньютона, ^[62]^{: 18–19} и объяснил цвета тонкой пластины как комбинированный эффект переднего и заднего отражений, которые усиливают или нейтрализуют друг друга в зависимости от длины волны и толщины. ^[62]^{: 37–39} Янг аналогичным образом объяснил цвета «полосатых поверхностей» (например, решеток ) как зависящее от длины волны усиление или подавление отражений от соседних линий. ^[62]^{: 35–37} Он описал это усиление или подавление как интерференцию .

Ни Ньютон, ни Гюйгенс не смогли удовлетворительно объяснить дифракцию — размытие и окантовку теней там, где, согласно прямолинейному распространению, они должны быть резкими. Ньютон, назвавший дифракцию «инфлекцией», предположил, что лучи света, проходящие вблизи препятствий, изгибаются («изгибаются»); но его объяснение было только качественным. ^[63] Конструкция общей касательной Гюйгенса без изменений вообще не могла объяснить дифракцию. Две такие модификации были предложены Янгом в той же Бейкерианской лекции 1801 года: во-первых, что вторичные волны вблизи края препятствия могут расходиться в тень, но только слабо, из-за ограниченного усиления от других вторичных волн; ^[62]^{: 25–27} и, во-вторых, что дифракция на краю была вызвана интерференцией двух лучей: один отражался от края, а другой изгибался при прохождении вблизи края. Последний луч не отклонялся бы, если бы находился достаточно далеко от края, но Юнг не подробно останавливался на этом случае. ^[62]^{: 42–44} Это были самые ранние предположения о том, что степень дифракции зависит от длины волны. ^[64] Позднее, в Бейкерианской лекции 1803 года, Юнг перестал рассматривать перегиб как отдельное явление, ^[65] и представил доказательства того, что дифракционные полосы внутри тени узкого препятствия были вызваны интерференцией: когда свет с одной стороны был заблокирован, внутренние полосы исчезали. ^[66] Но Юнг был одинок в таких усилиях, пока Френель не вошел в эту область. ^[67]

Гюйгенс, исследуя двойное преломление, заметил нечто, чего не мог объяснить: когда свет проходит через два одинаково ориентированных кристалла кальцита при нормальном падении, обыкновенный луч, выходящий из первого кристалла, испытывает только обычную рефракцию во втором, в то время как необыкновенный луч, выходящий из первого кристалла, испытывает только необыкновенную рефракцию во втором; но когда второй кристалл поворачивается на 90° относительно падающих лучей, роли меняются, так что обыкновенный луч, выходящий из первого кристалла, испытывает только необыкновенную рефракцию во втором, и наоборот. ^[68] Это открытие дало Ньютону еще одну причину отвергнуть волновую теорию: лучи света, очевидно, имели «стороны». ^[69] Корпускулы могли иметь стороны ^[70] (или полюса , как их позже назовут); но волны света не могли, ^[71] потому что (так казалось) любые такие волны должны были бы быть продольными (с колебаниями в направлении распространения). Ньютон предложил альтернативное «правило» для необычайной рефракции, ^[72] которое использовалось его авторитетом на протяжении всего XVIII века, хотя он не сделал «никаких известных попыток вывести его из каких-либо принципов оптики, корпускулярной или какой-либо другой». ^[73]^{: 327}

В 1808 году необычайная рефракция кальцита была экспериментально исследована с беспрецедентной точностью Этьеном-Луи Малюсом , и было обнаружено, что она согласуется со сфероидальной конструкцией Гюйгенса, а не с «правилом» Ньютона. ^[73] Малюс, поддержанный Пьером-Симоном Лапласом , ^[60]^{: 1146} затем попытался объяснить этот закон в корпускулярных терминах: из известного соотношения между направлениями падающего и преломленного лучей Малюс вывел корпускулярную скорость (как функцию направления), которая удовлетворяла бы принципу «наименьшего действия» Мопертюи . Но, как указал Юнг, существование такого закона скорости гарантировалось сфероидом Гюйгенса, потому что конструкция Гюйгенса приводит к принципу Ферма, который становится принципом Мопертюи, если скорость луча заменить на величину, обратную скорости частицы! Корпускуляристы не нашли закона силы , который бы дал предполагаемый закон скорости, за исключением кругового аргумента, в котором сила, действующая на поверхности кристалла, необъяснимым образом зависела от направления (возможно, последующей) скорости внутри кристалла. Хуже того, было сомнительно, что любая такая сила будет удовлетворять условиям принципа Мопертюи. ^[74] Напротив, Юнг продолжил показывать, что «среда, более легко сжимаемая в одном направлении, чем в любом направлении, перпендикулярном ей, как если бы она состояла из бесконечного числа параллельных пластин, соединенных веществом, несколько менее эластичным», допускает сфероидальные продольные волновые фронты, как и предполагал Гюйгенс. ^[75]

Печатная этикетка, видимая через двупреломляющий кристалл кальцита и современный поляризационный фильтр (повернута для демонстрации различной поляризации двух изображений)

Но Малус, в разгар своих экспериментов по двойному преломлению, заметил кое-что еще: когда луч света отражается от неметаллической поверхности под соответствующим углом, он ведет себя как один из двух лучей, выходящих из кристалла кальцита. ^[76] Именно Малус ввел термин поляризация для описания этого поведения, хотя поляризационный угол стал известен как угол Брюстера после того, как его зависимость от показателя преломления была экспериментально определена Дэвидом Брюстером в 1815 году. ^[77] Малус также ввел термин плоскость поляризации . В случае поляризации отражением его «плоскость поляризации» была плоскостью падающего и отраженного лучей; в современных терминах это плоскость, нормальная к электрическим колебаниям. В 1809 году Малус далее обнаружил, что интенсивность света, проходящего через два поляризатора, пропорциональна квадрату косинуса угла между их плоскостями поляризации ( закон Малуса ), ^[78] независимо от того, работают ли поляризаторы путем отражения или двойного преломления, и что все двулучепреломляющие кристаллы производят как необычайное преломление, так и поляризацию. ^[79] Когда корпускуляристы начали пытаться объяснить эти вещи в терминах полярных «молекул» света, у теоретиков волн не было рабочей гипотезы о природе поляризации, что побудило Юнга заметить, что наблюдения Малуса «представляют большие трудности для сторонников волновой теории, чем любые другие факты, с которыми мы знакомы». ^[80]

Малус умер в феврале 1812 года в возрасте 36 лет, вскоре после получения медали Рамфорда за свою работу по поляризации.

В августе 1811 года Франсуа Араго сообщил, что если тонкую пластину слюды рассматривать на фоне белой поляризованной подсветки через кристалл кальцита, то два изображения слюды будут иметь дополнительные цвета (наложение будет иметь тот же цвет, что и фон). Свет, выходящий из слюды, был « деполяризован » в том смысле, что не было ориентации кальцита, которая заставила бы одно изображение исчезнуть; однако это был не обычный (« неполяризованный ») свет, для которого два изображения были бы одного цвета. Вращение кальцита вокруг линии зрения изменяло цвета, хотя они оставались дополнительными. Вращение слюды изменяло насыщенность ( не оттенок) цветов. Это явление стало известно как хроматическая поляризация . Замена слюды гораздо более толстой пластиной кварца , грани которой были перпендикулярны оптической оси (оси сфероида Гюйгенса или функции скорости Малюса), производила аналогичный эффект, за исключением того, что вращение кварца не имело никакого значения. Араго попытался объяснить свои наблюдения в корпускулярных терминах. ^[81]

В 1812 году, когда Араго проводил дальнейшие качественные эксперименты и другие исследования, Жан-Батист Био переработал тот же самый фон, используя гипсовую пластину вместо слюды, и нашел эмпирические формулы для интенсивности обычных и необычных изображений. Формулы содержали два коэффициента, предположительно представляющие цвета лучей, «затронутых» и «незатронутых» пластиной — «затронутые» лучи имели ту же цветовую смесь, что и лучи, отраженные аморфными тонкими пластинами пропорциональной, но меньшей толщины. ^[82]

Араго протестовал, заявляя, что он сделал некоторые из тех же открытий, но не успел их описать. Фактически совпадение между работами Араго и Биота было минимальным, Араго был только качественным и более широким по охвату (попытка включить поляризацию отражением). Но спор спровоцировал печально известную ссору между двумя мужчинами. ^[83]^[84]

Позже в том же году Био попытался объяснить наблюдения как колебание выравнивания «затронутых» корпускул с частотой, пропорциональной частоте «припадков» Ньютона, из-за сил, зависящих от выравнивания. Эта теория стала известна как подвижная поляризация . Чтобы согласовать свои результаты с синусоидальным колебанием, Био пришлось предположить, что корпускулы возникали с одной из двух разрешенных ориентаций, а именно с крайностями колебания, с вероятностями, зависящими от фазы колебания . ^[85] Корпускулярная оптика становилась дорогой на предположениях. Но в 1813 году Био сообщил, что случай кварца был проще: наблюдаемое явление (теперь называемое оптическим вращением или оптической активностью , а иногда и вращательной поляризацией ) было постепенным вращением направления поляризации с расстоянием и могло быть объяснено соответствующим вращением ( не колебанием) корпускул. ^[86]

В начале 1814 года, рассматривая работу Биота по хроматической поляризации, Юнг отметил, что периодичность цвета как функция толщины пластины, включая фактор, на который период превышает период для отражающей тонкой пластины, и даже эффект наклона пластины (но не роль поляризации), может быть объяснена волновой теорией с точки зрения различного времени распространения обыкновенных и необыкновенных волн через пластину. ^[87] Но Юнг был тогда единственным публичным защитником волновой теории. ^[88]

Подводя итог, можно сказать, что весной 1814 года, когда Френель тщетно пытался угадать, что такое поляризация, корпускуляристы думали, что знают, в то время как волновые теоретики (если можно использовать множественное число) буквально не имели об этом ни малейшего представления. Обе теории претендовали на объяснение прямолинейного распространения, но волновое объяснение было в подавляющем большинстве сочтено неубедительным. Корпускулярная теория не могла строго связать двойное преломление с поверхностными силами; волновая теория еще не могла связать его с поляризацией. Корпускулярная теория была слаба на тонких пластинах и молчала на решетках; ^{[Примечание 2]} волновая теория была сильна на обоих, но недооценена. Что касается дифракции, корпускулярная теория не давала количественных предсказаний, в то время как волновая теория начала делать это, рассматривая дифракцию как проявление интерференции, но рассматривала только два луча одновременно. Только корпускулярная теория давала хотя бы смутное представление об угле Брюстера, законе Малюса или оптическом вращении. Что касается хроматической поляризации, волновая теория объясняла периодичность гораздо лучше, чем корпускулярная теория, но ничего не могла сказать о роли поляризации; и ее объяснение периодичности в значительной степени игнорировалось. ^[89] И Араго основал изучение хроматической поляризации, только чтобы уступить лидерство, что спорно, Биоту. Таковы были обстоятельства, при которых Араго впервые услышал об интересе Френеля к оптике.

Rêveries

Письма Френеля, написанные позднее в 1814 году, показывают его интерес к волновой теории, включая его понимание того, что она объясняет постоянство скорости света и, по крайней мере, совместима со звездной аберрацией. В конце концов он составил то, что он называл своими rêveries (размышлениями), в эссе и отправил его через Леонор Мериме Андре-Мари Амперу , который не ответил напрямую. Но 19 декабря Мериме обедал с Ампером и Араго, с которыми он был знаком по Политехнической школе; и Араго обещал взглянуть на эссе Френеля. ^[90]^{[Примечание 3]}

В середине 1815 года, по пути домой в Матье, чтобы отбыть отстранение, Френель встретился с Араго в Париже и рассказал ему о волновой теории и звездной аберрации. Ему сообщили, что он пытается выломать открытые двери (" il enfonçait des portes ouvertes "), и направили к классическим работам по оптике. ^[91]

Дифракция

Первая попытка (1815)

12 июля 1815 года, когда Френель собирался покинуть Париж, Араго оставил ему записку на новую тему:

Я не знаю ни одной книги, которая содержала бы все эксперименты, которые физики проводят по дифракции света. Мсье Френель сможет познакомиться с этой частью оптики, только прочитав труд Гримальди , труд Ньютона, английский трактат Джордана ^[92] и мемуары Брума и Янга, которые являются частью собрания Philosophical Transactions^[93] .

Френель не имел бы свободного доступа к этим работам за пределами Парижа и не мог читать по-английски. ^[94] Но в Матье — с точечным источником света, сделанным путем фокусировки солнечного света с помощью капли меда, грубым микрометром собственной конструкции и вспомогательным аппаратом, сделанным местным слесарем, — он начал свои собственные эксперименты. ^[95] Его метод был новым: в то время как предыдущие исследователи проецировали полосы на экран, Френель вскоре отказался от экрана и наблюдал полосы в пространстве, через линзу с микрометром в фокусе, что позволяло проводить более точные измерения, требуя при этом меньше света. ^[96]

Позже в июле, после окончательного поражения Наполеона, Френель был восстановлен в должности с преимуществом поддержки победившей стороны. Он запросил двухмесячный отпуск, который был легко предоставлен, поскольку дорожные работы были приостановлены. ^[97]

23 сентября он написал Араго, начав со слов: «Я думаю, что нашел объяснение и закон цветных полос, которые можно заметить в тенях тел, освещенных светящейся точкой». Однако в том же абзаце Френель неявно признал сомнение относительно новизны своей работы: отметив, что ему придется понести некоторые расходы, чтобы улучшить свои измерения, он хотел узнать, «не бесполезно ли это, и не установлен ли уже закон дифракции достаточно точными экспериментами». ^[98] Он объяснил, что у него еще не было возможности приобрести предметы из своих списков для чтения, ^[94] за явным исключением «книги Юнга», которую он не мог понять без помощи своего брата. ^[99]^{[Примечание 4]} Неудивительно, что он повторил многие шаги Юнга.

В мемуарах, отправленных в институт 15 октября 1815 года, Френель нанес на карту внешние и внутренние полосы в тени проволоки. Он заметил, как и Юнг до него, что внутренние полосы исчезали, когда свет с одной стороны был заблокирован, и пришел к выводу, что «колебания двух лучей, пересекающихся под очень малым углом, могут противоречить друг другу…» ^[100] Но, в то время как Юнг воспринял исчезновение внутренних полос как подтверждение принципа интерференции, Френель сообщил, что именно внутренние полосы первыми привлекли его внимание к этому принципу. Чтобы объяснить дифракционную картину, Френель построил внутренние полосы, рассматривая пересечения круговых волновых фронтов, испускаемых двумя краями препятствия, а внешние полосы, рассматривая пересечения между прямыми волнами и волнами, отраженными от ближнего края. Для внешних полос, чтобы получить приемлемое согласие с наблюдением, он должен был предположить, что отраженная волна была инвертированной ; и он отметил, что предсказанные пути полос были гиперболическими. В той части мемуаров, которая наиболее явно превзошла Юнга, Френель объяснил обычные законы отражения и преломления в терминах интерференции, отметив, что если два параллельных луча отражаются или преломляются под углом, отличным от предписанного, они больше не будут иметь ту же самую фазу в общей перпендикулярной плоскости, и каждая вибрация будет отменена близлежащей вибрацией. Он отметил, что его объяснение было верным при условии, что неровности поверхности были намного меньше длины волны. ^[101]

10 ноября Френель отправил дополнительную записку, посвященную кольцам Ньютона и решеткам, ^[102] включая, впервые, пропускающие решетки, хотя в этом случае интерферирующие лучи все еще предполагались «отклоненными», а экспериментальная проверка была недостаточной, поскольку использовались только две нити. ^[103]

Поскольку Френель не был членом института, судьба его мемуаров во многом зависела от отчета одного члена. Репортером мемуаров Френеля оказался Араго ( другим рецензентом был Пуансо ). ^[104] 8 ноября Араго написал Френелю:

Институт поручил мне изучить ваши мемуары о дифракции света; я внимательно их изучил и нашел много интересных экспериментов, некоторые из которых уже были проведены доктором Томасом Янгом, который в целом рассматривает это явление способом, довольно аналогичным тому, который приняли вы. Но ни он, ни кто-либо другой до вас не видели, что внешние цветные полосы не движутся по прямой линии по мере удаления от непрозрачного тела. Результаты, которых вы достигли в этом отношении, кажутся мне очень важными; возможно, они могут послужить доказательством истинности волновой системы, с которой так часто и так слабо боролись физики, не потрудившиеся ее понять. ^[105]

Френель был обеспокоен, желая узнать точнее, где он столкнулся с Юнгом. ^[106] Что касается изогнутых путей «цветных полос», Юнг отметил гиперболические пути полос в интерференционной картине с двумя источниками , примерно соответствующие внутренним полосам Френеля , и описал гиперболические полосы, которые появляются на экране внутри прямоугольных теней. ^[107] Он не упомянул изогнутые пути внешних полос тени; но, как он позже объяснил, ^[108] это было потому, что Ньютон уже сделал это. ^[109] Ньютон, очевидно, думал, что полосы были каустиками . Таким образом, Араго ошибался, полагая, что изогнутые пути полос были принципиально несовместимы с корпускулярной теорией. ^[110]

Письмо Араго продолжало запрашивать больше данных о внешних границах. Френель подчинился, пока не исчерпал свой отпуск и не был назначен в Ренн в департаменте Иль и Вилен . В этот момент Араго ходатайствовал перед Гаспаром де Прони , главой Школы мостов, который написал Луи-Матье Моле , главе Корпуса мостов, предполагая, что прогресс науки и престиж Корпуса будут усилены, если Френель сможет приехать в Париж на некоторое время. Он прибыл в марте 1816 года, и его отпуск впоследствии был продлен до середины года. ^[111]

Между тем, в эксперименте, о котором сообщалось 26 февраля 1816 года, Араго подтвердил предсказание Френеля о том, что внутренние полосы смещаются, если лучи с одной стороны препятствия проходят через тонкую стеклянную пластину. Френель правильно приписал это явление более низкой скорости волны в стекле. ^[112] Позднее Араго использовал аналогичный аргумент для объяснения цветов в мерцании звезд. ^{[Примечание 5]}

Обновленные мемуары Френеля ^[113] в конечном итоге были опубликованы в выпуске Annales de Chimie et de Physique за март 1816 года , соредактором которого недавно стал Араго. ^[114] Этот выпуск фактически не появился до мая. ^[115] В марте у Френеля уже были конкуренты: Био прочитал мемуары о дифракции, написанные им самим и его учеником Клодом Пуйе , содержащие обширные данные и утверждающие, что регулярность дифракционных полос, как и регулярность колец Ньютона, должна быть связана с «припадками» Ньютона. Но новая связь не была строгой, и сам Пуйе стал выдающимся ранним последователем волновой теории. ^[116]

«Действительный луч», эксперимент с двойным зеркалом (1816)

24 мая 1816 года Френель написал Янгу (на французском языке), признавая, как мало нового было в его собственных мемуарах. ^[118] Но в «дополнении», подписанном 14 июля и прочитанном на следующий день, ^[119] Френель отметил, что внутренние полосы были более точно предсказаны, если предположить, что два интерферирующих луча пришли с некоторого расстояния за пределами краев препятствия. Чтобы объяснить это, он разделил падающий волновой фронт на препятствие на то, что мы теперь называем зонами Френеля , так что вторичные волны из каждой зоны были распределены на половину цикла, когда они достигли точки наблюдения. Зоны на одной стороне препятствия в значительной степени уравновешивались парами, за исключением первой зоны, которая была представлена «эффективным лучом». Этот подход работал для внутренних полос, но суперпозиция эффективного луча и прямого луча не работала для внешних полос. ^[120]

Считалось, что вклад «эффективного луча» был лишь частично отменен по причинам, связанным с динамикой среды: там, где волновой фронт был непрерывным, симметрия запрещала наклонные колебания; но вблизи препятствия, которое обрезало волновой фронт, асимметрия допускала некоторые боковые колебания в направлении геометрической тени. Этот аргумент показал, что Френель (еще) не полностью принял принцип Гюйгенса, который допускал наклонное излучение со всех участков фронта. ^[121]

В том же дополнении Френель описал свое известное двойное зеркало, состоящее из двух плоских зеркал, соединенных под углом чуть меньше 180°, с помощью которых он создавал двухщелевую интерференционную картину из двух виртуальных изображений одной и той же щели. Обычный эксперимент с двумя щелями требовал предварительной одинарной щели, чтобы гарантировать, что свет, падающий на двойную щель, был когерентным (синхронизированным). В версии Френеля предварительная одинарная щель была сохранена, а двойная щель была заменена двойным зеркалом, которое не имело физического сходства с двойной щелью, но при этом выполняло ту же функцию. Этот результат (который был объявлен Араго в мартовском выпуске Annales ) заставил с трудом поверить, что двухщелевая картина имела какое-либо отношение к корпускулам, отклоняющимся при прохождении вблизи краев щелей. ^[122]

Но 1816 год стал « Годом без лета »: урожай не урожаев; голодные фермерские семьи выстроились вдоль улиц Ренна; центральное правительство организовало «благотворительные работные дома» для нуждающихся; и в октябре Френеля отправили обратно в Иль и Вилен, чтобы он руководил работниками благотворительной организации в дополнение к его постоянной дорожной бригаде. ^[123] По словам Араго,

с Френелем добросовестность всегда была важнейшей частью его характера, и он постоянно исполнял свои обязанности инженера с самой строгой скрупулезностью. Миссия защищать доходы государства, чтобы получить для них наилучшее возможное применение, представала перед его глазами в свете вопроса чести. Чиновник, каков бы ни был его ранг, который представлял ему двусмысленный отчет, сразу становился объектом его глубокого презрения. … При таких обстоятельствах привычная мягкость его манер исчезала… ^[124]

Письма Френеля от декабря 1816 года раскрывают его последующую тревогу. Араго он жаловался на то, что его «изводят заботы надзора и необходимость выговаривать…» А Мериме он писал: «Я не нахожу ничего более утомительного, чем управлять другими людьми, и признаюсь, что понятия не имею, что делаю». ^[125]

Премия мемуары (1818) и продолжение

17 марта 1817 года Академия наук объявила, что дифракция станет темой двухгодичного Гран-при по физике, который будет присуждаться в 1819 году. ^[126] Крайний срок подачи заявок был установлен на 1 августа 1818 года, чтобы дать время для повторения экспериментов. Хотя формулировка задачи относилась к лучам и перегибу и не предполагала решений на основе волн, Араго и Ампер призвали Френеля принять участие. ^[127]

Осенью 1817 года Френель, при поддержке де Прони, получил отпуск от нового главы Corp des Ponts Луи Беккея и вернулся в Париж. ^[128] Он возобновил свои инженерные обязанности весной 1818 года; но с тех пор он обосновался в Париже, ^[129] сначала на канале Урк , ^[130] а затем (с мая 1819 года) с кадастром мостовых. ^[131]^[132]^{: 486}

15 января 1818 года в другом контексте (повторно рассмотренном ниже) Френель показал, что сложение синусоидальных функций одинаковой частоты, но разных фаз аналогично сложению сил с разными направлениями. ^[133] Его метод был похож на представление фазора , за исключением того, что «силы» были плоскими векторами, а не комплексными числами ; их можно было складывать и умножать на скаляры , но (пока) не умножать и делить друг на друга. Объяснение было алгебраическим, а не геометрическим.

Знание этого метода предполагалось в предварительной заметке о дифракции ^[134], датированной 19 апреля 1818 года и поданной 20 апреля, в которой Френель изложил элементарную теорию дифракции, как она представлена в современных учебниках. Он переформулировал принцип Гюйгенса в сочетании с принципом суперпозиции , заявив, что вибрация в каждой точке волнового фронта является суммой вибраций, которые были бы посланы ей в этот момент всеми элементами волнового фронта в любом из его предыдущих положений, причем все элементы действуют по отдельности (см. принцип Гюйгенса-Френеля ) . Для волнового фронта, частично заблокированного в предыдущем положении, суммирование должно было проводиться по незаблокированной части. В направлениях, отличных от нормали к первичному волновому фронту, вторичные волны ослаблялись из-за наклона, но ослаблялись гораздо больше из-за деструктивной интерференции, так что эффект одного только наклона можно было игнорировать. ^[135] Для дифракции на прямом крае интенсивность как функция расстояния от геометрической тени могла бы быть выражена с достаточной точностью в терминах того, что сейчас называется нормализованными интегралами Френеля :

Дифракционные полосы вблизи границы геометрической тени прямой грани. Интенсивность света рассчитывалась по значениям нормализованных интегралов C ( x ) , S ( x )

C(x)=\!\int _{0}^{x}\!\cos {\big (}{\tfrac {1}{2}}\pi z^{2}{\big )}\,dz

S(x)=\!\int _{0}^{x}\!\sin {\big (}{\tfrac {1}{2}}\pi z^{2}{\big )}\,dz\,.

В той же заметке была приведена таблица интегралов для верхнего предела от 0 до 5,1 с шагом 0,1, вычисленная со средней ошибкой 0,0003 ^[136] , а также меньшая таблица максимумов и минимумов результирующей интенсивности.

В своем последнем «Мемуаре о дифракции света» ^[137] , депонированном 29 июля ^[138] и снабженном латинским эпиграфом « Natura simplex et fecunda » («Природа простая и плодородная»), ^[139] Френель немного расширил две таблицы, не меняя существующие цифры, за исключением поправки к первому минимуму интенсивности. Для полноты он повторил свое решение «проблемы интерференции», посредством которой синусоидальные функции добавляются как векторы. Он признал направленность вторичных источников и изменение их расстояний от точки наблюдения, главным образом для того, чтобы объяснить, почему эти вещи имеют пренебрежимо малое значение в контексте, при условии, конечно, что вторичные источники не излучают в ретроградном направлении. Затем, применив свою теорию интерференции к вторичным волнам, он выразил интенсивность света, дифрагированного одним прямым краем (полуплоскостью), в терминах интегралов, которые включали размеры задачи, но которые можно было преобразовать в нормализованные формы выше. Ссылаясь на интегралы, он объяснил расчет максимумов и минимумов интенсивности (внешних полос) и отметил, что рассчитанная интенсивность очень быстро падает по мере приближения к геометрической тени. ^[140] Последний результат, как говорит Оливье Дарриголь, «равнозначен доказательству прямолинейного распространения света в волновой теории, и это действительно первое доказательство, которое современный физик все еще принимает». ^[141]

Для экспериментальной проверки своих расчетов Френель использовал красный свет с длиной волны 638 нм, который он вывел из картины дифракции в простом случае, когда свет, падающий на одну щель, фокусировался цилиндрической линзой. Для различных расстояний от источника до препятствия и от препятствия до точки поля он сравнивал рассчитанные и наблюдаемые положения полос при дифракции на полуплоскости, щели и узкой полоске, концентрируясь на минимумах, которые были визуально более резкими, чем максимумы. Для щели и полосы он не мог использовать ранее вычисленную таблицу максимумов и минимумов; для каждой комбинации измерений интенсивность должна была быть выражена в терминах сумм или разностей интегралов Френеля и рассчитана по таблице интегралов, а экстремумы должны были быть рассчитаны заново. ^[142] Согласие между расчетом и измерением было лучше, чем 1,5% почти в каждом случае. ^[143]

Ближе к концу своих мемуаров Френель подытожил разницу между использованием вторичных волн Гюйгенсом и его собственным: в то время как Гюйгенс говорит, что свет есть только там, где вторичные волны точно совпадают, Френель говорит, что полная тьма есть только там, где вторичные волны точно нейтрализуются. ^[144]

В состав жюри вошли Лаплас, Био и Пуассон (все корпускуляристы), Гей-Люссак (независимый) и Араго, который в конечном итоге написал отчет комитета. ^[145] Хотя заявки на участие в конкурсе должны были быть анонимными для судей, работа Френеля должна была быть узнаваема по содержанию. ^[146] Была только одна другая заявка, от которой не сохранилось ни рукописи, ни каких-либо записей об авторе. ^[147] Эта заявка (обозначенная как «№ 1») была упомянута только в последнем абзаце отчета судей, ^[148] отмечая, что автор проявил незнание соответствующих более ранних работ Юнга и Френеля, использовал недостаточно точные методы наблюдения, упустил из виду известные явления и допустил очевидные ошибки. По словам Джона Уорралла , «конкуренция, с которой столкнулся Френель, вряд ли могла быть менее жесткой». ^[149] Мы можем сделать вывод, что у комитета было только два варианта: присудить премию Френелю («№ 2») или не присудить ее. ^[150]

Комитет обсудил новый год. ^[151]^{: 144} Затем Пуассон, используя случай, в котором теория Френеля давала простые интегралы, предсказал, что если круглое препятствие освещается точечным источником, то должно быть (согласно теории) яркое пятно в центре тени, освещенное так же ярко, как и внешняя сторона. Это, кажется, было задумано как reductio ad absurdum . Араго, не смутившись, собрал эксперимент с препятствием диаметром 2 мм — и там, в центре тени, было пятно Пуассона . ^[152]

Единогласный ^[153] отчет комитета, ^[154] зачитанный на заседании Академии 15 марта 1819 года, ^[155] присудил премию «мемуару, обозначенному номером 2 и содержащему в качестве эпиграфа: Natura simplex et fecunda ». ^[156] На том же заседании, ^[157]^{: 427} после вынесения решения, президент Академии вскрыл запечатанную записку, приложенную к мемуару, в которой автором был указан Френель. ^[158] Награда была объявлена на открытом заседании Академии неделю спустя, 22 марта. ^[157]^{: 432}

Проверка Араго контринтуитивного предсказания Пуассона вошла в фольклор, как будто она решила судьбу приза. ^[159] Однако эта точка зрения не поддерживается отчетом судей, в котором этому вопросу отведено всего два предложения в предпоследнем абзаце. ^[160] Триумф Френеля также не сразу обратил Лапласа, Био и Пуассона в волновую теорию, ^[161] по крайней мере по четырем причинам. Во-первых, хотя профессионализация науки во Франции установила общие стандарты, одно дело было признать часть исследования соответствующей этим стандартам, а другое — считать ее окончательной. ^[88] Во-вторых, можно было интерпретировать интегралы Френеля как правила объединения лучей . Араго даже поощрял такую интерпретацию, предположительно, для того, чтобы свести к минимуму сопротивление идеям Френеля. ^[162] Даже Био начал преподавать принцип Гюйгенса-Френеля, не связывая себя с волновой основой. ^[163] В-третьих, теория Френеля не объясняла адекватно механизм генерации вторичных волн или то, почему они имели значительный угловой разброс; этот вопрос особенно беспокоил Пуассона. ^[164] В-четвертых, вопрос, который волновал большинство физиков-оптиков в то время, был не дифракцией, а поляризацией, над которой работал Френель, но еще не совершил своего решающего прорыва.

Поляризация

Предыстория: эмиссионизм и селекционизм

Эмиссионная теория света рассматривала распространение света как перенос некоторого вида материи. Хотя корпускулярная теория была, очевидно, эмиссионной теорией, обратного не следовало: в принципе, можно было быть эмиссионистом, не будучи корпускуляристом. Это было удобно, потому что, помимо обычных законов отражения и преломления, эмиссионисты никогда не могли сделать проверяемые количественные предсказания из теории сил, действующих на корпускулы света. Но они делали количественные предсказания из предпосылок, что лучи являются счетными объектами, которые сохраняются в их взаимодействии с материей (за исключением поглощающих сред) и которые имеют определенную ориентацию относительно направления их распространения. Согласно этой структуре, поляризация и связанные с ней явления двойного преломления и частичного отражения включали изменение ориентации лучей и/или их выбор в соответствии с ориентацией, а состояние поляризации луча (пучка лучей) было вопросом того, сколько лучей было в какой ориентации: в полностью поляризованном луче все ориентации были одинаковыми. Этот подход, который Джед Бухвальд назвал селекционизмом , был впервые предложен Малусом и усердно продолжен Биотом. ^[165]^[84]^{: 110–113}

Френель, напротив, решил ввести поляризацию в эксперименты по интерференции.

Интерференция поляризованного света, хроматическая поляризация (1816–21)

В июле или августе 1816 года Френель обнаружил, что когда двулучепреломляющий кристалл создавал два изображения одной щели, он не мог получить обычную двухщелевую интерференционную картину, даже если он компенсировал различное время распространения. Более общий эксперимент, предложенный Араго, обнаружил, что если два луча двухщелевого устройства были поляризованы отдельно, интерференционная картина появлялась и исчезала, когда поляризация одного луча вращалась, давая полную интерференцию для параллельных поляризаций, но не интерференцию для перпендикулярных поляризаций (см. законы Френеля-Араго ) . ^[166] Эти эксперименты, среди прочих, были в конечном итоге описаны в кратком мемуаре, опубликованном в 1819 году и позже переведенном на английский язык. ^[167]

В мемуарах, составленных 30 августа 1816 года и пересмотренных 6 октября, Френель сообщил об эксперименте, в котором он поместил две соответствующие тонкие пластины в двухщелевой аппарат — по одной над каждой щелью, с их оптическими осями, перпендикулярными — и получил две интерференционные картины, смещенные в противоположных направлениях, с перпендикулярными поляризациями. Это, в сочетании с предыдущими открытиями, означало, что каждая пластина разделяла падающий свет на перпендикулярно поляризованные компоненты с разными скоростями — так же, как обычный (толстый) двупреломляющий кристалл, и вопреки гипотезе Биота о «подвижной поляризации». ^[168]

Соответственно, в тех же мемуарах Френель предложил свою первую попытку волновой теории хроматической поляризации. Когда поляризованный свет проходил через кристаллическую пластину, он разделялся на обыкновенные и необыкновенные волны (с интенсивностями, описанными законом Малуса), и они были перпендикулярно поляризованы и, следовательно, не интерферировали, так что никаких цветов не создавалось (пока). Но если они затем проходили через анализатор ( второй поляризатор), их поляризации приводились в соответствие (с интенсивностями, снова измененными в соответствии с законом Малуса), и они интерферировали. ^[169] Это объяснение само по себе предсказывает, что если анализатор повернуть на 90°, обыкновенные и необыкновенные волны просто меняются ролями, так что если анализатор принимает форму кристалла кальцита, два изображения пластины должны быть одного и того же оттенка (этот вопрос рассматривается ниже). Но на самом деле, как обнаружили Араго и Био, они имеют дополнительные цвета. Чтобы исправить предсказание, Френель предложил правило инверсии фазы, согласно которому одна из составляющих волн одного из двух изображений претерпевала дополнительный сдвиг фазы на 180° на своем пути через пластину. Эта инверсия была слабостью теории по сравнению с теорией Биота, как признал Френель, ^[170] хотя правило указывало, какое из двух изображений имело инвертированную волну. ^[171] Более того, Френель мог иметь дело только с особыми случаями, поскольку он еще не решил проблему наложения синусоидальных функций с произвольными разностями фаз из-за распространения с разными скоростями через пластину. ^[172]

Он решил эту проблему в «дополнении», подписанном 15 января 1818 года ^[133] (упомянутом выше). В том же документе он приспособил закон Малуса, предложив базовый закон: если поляризованный свет падает на двупреломляющий кристалл с его оптической осью под углом θ к «плоскости поляризации», то обычные и необыкновенные колебания (как функции времени) масштабируются факторами cos θ и sin θ соответственно. Хотя современные читатели легко интерпретируют эти факторы в терминах перпендикулярных компонентов поперечного колебания, Френель (еще) не объяснял их таким образом. Следовательно, ему все еще требовалось правило инверсии фазы. Он применил все эти принципы к случаю хроматической поляризации, не охватываемому формулами Био, включающему две последовательные пластины с осями, разделенными на 45°, и получил предсказания, которые не соответствовали экспериментам Био (за исключением особых случаев), но соответствовали его собственным. ^[173]

Френель применил те же принципы к стандартному случаю хроматической поляризации, в котором одна двулучепреломляющая пластина была разрезана параллельно своей оси и помещена между поляризатором и анализатором. Если анализатор принимал форму толстого кристалла кальцита с осью в плоскости поляризации, Френель предсказал, что интенсивности обычных и необычных изображений пластины были соответственно пропорциональны

I_{o}=\cos ^{2}i\,\cos ^{2}(i{-}s)+\sin ^{2}i\,\sin ^{2}(i{-}s)+{\tfrac {1}{2}}\sin 2i\,\sin 2(i{-}s)\cos \phi \,,

I_{e}=\cos ^{2}i\,\sin ^{2}(i{-}s)+\sin ^{2}i\,\cos ^{2}(i{-}s)-{\tfrac {1}{2}}\sin 2i\,\sin 2(i{-}s)\cos \phi \,,

где - угол между начальной плоскостью поляризации и оптической осью пластины, - угол между начальной плоскостью поляризации и плоскостью поляризации конечного обыкновенного изображения, а - фазовая задержка необыкновенной волны относительно обыкновенной волны из-за разницы во времени распространения через пластину. Члены в являются частотно-зависимыми членами и объясняют, почему пластина должна быть тонкой , чтобы производить различимые цвета: если пластина слишком толстая, она будет проходить через слишком много циклов, поскольку частота изменяется в видимом диапазоне, и глаз (который делит видимый спектр только на три полосы ) не сможет разрешить циклы. $i$ $s$ $\phi$ $\phi$ $\cos \phi$

Из этих уравнений легко проверить, что для всех так что цвета являются дополнительными. Без правила инверсии фаз перед последним членом во втором уравнении стоял бы знак плюс , так что -зависимый член был бы одинаковым в обоих уравнениях, подразумевая (неверно), что цвета имеют одинаковый оттенок. $\,I_{o}+I_{e}=1\,$ $\phi ,$ $\phi$

Эти уравнения были включены в недатированную записку, которую Френель дал Биоту, ^[174] к которой Биот добавил несколько собственных строк. Если мы подставим

U=\cos ^{2}{\tfrac {\phi }{2}}

A=\sin ^{2}{\tfrac {\phi }{2}}\,,

тогда формулы Френеля можно переписать как

\!I_{o}=U\cos ^{2}s+A\cos ^{2}(2i-s)\,,

I_{e}=U\sin ^{2}s+A\sin ^{2}(2i-s)\,,

которые являются ничем иным, как эмпирическими формулами Биота 1812 года ^[175], за исключением того, что Биот интерпретировал и как «незатронутые» и «затронутые» выборки лучей, падающих на пластинку. Если бы подстановки Биота были точны, они бы подразумевали, что его экспериментальные результаты более полно объяснялись теорией Френеля, чем его собственной. $U$ $A$

Араго отложил сообщение о работах Френеля по хроматической поляризации до июня 1821 года, когда он использовал их в широкой атаке на теорию Био. В своем письменном ответе Био протестовал, что атака Араго вышла за рамки надлежащего объема отчета о номинированных работах Френеля. Но Био также утверждал, что замены для и и, следовательно, выражения Френеля для и были эмпирически неверны, потому что, когда интенсивности спектральных цветов Френеля смешивались в соответствии с правилами Ньютона, квадраты косинуса и синуса менялись слишком плавно, чтобы объяснить наблюдаемую последовательность цветов. Это утверждение вызвало письменный ответ Френеля, ^[176] который оспаривал, действительно ли цвета менялись так резко, как утверждал Био, ^[177] и может ли человеческий глаз судить о цвете с достаточной объективностью для этой цели. По последнему вопросу Френель указал, что разные наблюдатели могут давать разные названия одному и тому же цвету. Более того, он сказал, что один наблюдатель может сравнивать цвета только бок о бок; и даже если они считаются одинаковыми, идентичность — это ощущение, а не обязательно состав. ^[178] Старейший и самый сильный довод Френеля — что тонкие кристаллы подчиняются тем же законам, что и толстые, и не нуждаются в отдельной теории или не допускают ее — Био оставил без ответа. Араго и Френель, как считалось, выиграли спор. ^[179] $U$ $A,$ $I_{o}$ $I_{e},$

Более того, к этому времени у Френеля появилось новое, более простое объяснение его уравнений хроматической поляризации.

Прорыв: Чистые поперечные волны (1821)

В черновике мемуаров от 30 августа 1816 года Френель упомянул две гипотезы, одну из которых он приписал Амперу, согласно которым неинтерференция ортогонально поляризованных лучей могла бы быть объяснена, если бы поляризованные световые волны были частично поперечными . Но Френель не смог развить ни одну из этих идей в комплексную теорию. Еще в сентябре 1816 года, согласно его более позднему отчету, ^[180] он понял, что неинтерференция ортогонально поляризованных лучей вместе с правилом инверсии фазы в хроматической поляризации была бы наиболее легко объяснена, если бы волны были чисто поперечными, и Ампер «имел ту же самую мысль» о правиле инверсии фазы. Но это породило бы новую трудность: поскольку естественный свет, по-видимому, не поляризован, а его волны, следовательно, предполагались продольными, необходимо было бы объяснить, как продольная составляющая вибрации исчезала при поляризации и почему она не появлялась снова, когда поляризованный свет отражался или преломлялся наклонно стеклянной пластиной. ^[181]

Независимо от этого, 12 января 1817 года, Юнг написал Араго (на английском языке), отметив, что поперечная вибрация будет представлять собой поляризацию, и что если две продольные волны пересекаются под значительным углом, они не могут гаситься, не оставляя остаточной поперечной вибрации. ^[182] Юнг повторил эту идею в статье, опубликованной в приложении к Encyclopaedia Britannica в феврале 1818 года, в которой он добавил, что закон Малуса будет объяснен, если поляризация будет заключаться в поперечном движении. ^[183]^{: 333–335}

Таким образом, Френель, по его собственному свидетельству, возможно, не был первым человеком, который заподозрил, что световые волны могут иметь поперечную составляющую , или что поляризованные волны являются исключительно поперечными. И именно Юнг, а не Френель, первым опубликовал идею о том, что поляризация зависит от ориентации поперечной вибрации. Но эти неполные теории не примирили природу поляризации с очевидным существованием неполяризованного света; это достижение должно было быть только у Френеля.

В заметке, которую Бухвальд датирует летом 1818 года, Френель размышлял о том, что неполяризованные волны могут иметь колебания с одинаковой энергией и наклоном, с их ориентацией, распределенной равномерно относительно нормали волны, и что степень поляризации является степенью неравномерности распределения . Двумя страницами позже он отметил, по-видимому, впервые в письменной форме, что его правило инверсии фазы и неинтерференция ортогонально поляризованных лучей можно было бы легко объяснить, если бы колебания полностью поляризованных волн были «перпендикулярны нормали к волне», то есть чисто поперечными. ^[184]

Но если он мог объяснить отсутствие поляризации, усреднив поперечный компонент, ему не нужно было также предполагать продольный компонент. Достаточно было предположить, что световые волны являются чисто поперечными, следовательно, всегда поляризованными в смысле наличия определенной поперечной ориентации, и что «неполяризованное» состояние естественного или «прямого» света обусловлено быстрыми и случайными изменениями в этой ориентации, и в этом случае две когерентные порции «неполяризованного» света все равно будут интерферировать, поскольку их ориентации будут синхронизированы.

Неизвестно точно, когда Френель сделал этот последний шаг, поскольку нет соответствующей документации за 1820 или начало 1821 года ^[185] (возможно, потому что он был слишком занят работой над прототипами линз маяка; см. ниже). Но он впервые опубликовал эту идею в статье « Calcul des teintes… » («расчет оттенков…»), опубликованной в Annales Араго в мае, июне и июле 1821 года. ^[186] В первой части Френель описал «прямой» (неполяризованный) свет как «быструю последовательность систем волн, поляризованных во всех направлениях» ^[187] и дал то, что по сути является современным объяснением хроматической поляризации, хотя и в терминах аналогии между поляризацией и разрешением сил в плоскости, упомянув поперечные волны только в сноске. Введение поперечных волн в основной аргумент было отложено до второй части, в которой он раскрыл подозрение, которое он и Ампер питали с 1816 года, и трудности, которые оно вызывало. ^[188] Он продолжил:

Только несколько месяцев спустя, более внимательно размышляя над этим вопросом, я понял, что весьма вероятно, что колебательные движения световых волн совершаются исключительно вдоль плоскости этих волн, как для прямого света, так и для поляризованного света . ^[189]^{[Примечание 6]}

Согласно этому новому взгляду, писал он, «акт поляризации состоит не в создании этих поперечных движений, а в разложении их на два фиксированных перпендикулярных направления и в разделении двух компонентов» ^{[190] .}

В то время как селекционисты могли настаивать на интерпретации дифракционных интегралов Френеля в терминах дискретных, счетных лучей, они не могли сделать то же самое с его теорией поляризации. Для селекциониста состояние поляризации луча касалось распределения ориентаций по популяции лучей , и это распределение предполагалось статичным. Для Френеля состояние поляризации луча касалось изменения смещения с течением времени . Это смещение могло быть ограничено, но не было статичным, и лучи были геометрическими конструкциями, а не счетными объектами. Концептуальный разрыв между волновой теорией и селекционизмом стал непреодолимым. ^[191]

Другая трудность, связанная с чисто поперечными волнами, конечно, заключалась в очевидном следствии того, что эфир был упругим твердым телом , за исключением того, что, в отличие от других упругих твердых тел, он не был способен передавать продольные волны. ^{[Примечание 7]} Волновая теория была дешева в предположениях, но ее последнее предположение было дорогим в доверчивости. ^[192] Если бы это предположение было широко принято, его объяснительная сила должна была бы быть впечатляющей.

Частичное отражение (1821)

Во второй части «Calcul des teintes» (июнь 1821 г.) Френель предположил, по аналогии со звуковыми волнами, что плотность эфира в преломляющей среде обратно пропорциональна квадрату скорости волны и, следовательно, прямо пропорциональна квадрату показателя преломления. Для отражения и преломления на поверхности между двумя изотропными средами с разными показателями Френель разложил поперечные колебания на две перпендикулярные компоненты, теперь известные как компоненты s и p , которые параллельны поверхности и плоскости падения соответственно; другими словами, компоненты s и p соответственно квадратны и параллельны плоскости падения. ^{[Примечание 8]} Для компонента s Френель предположил, что взаимодействие между двумя средами аналогично упругому столкновению , и получил формулу для того, что мы теперь называем отражательной способностью : отношение отраженной интенсивности к падающей интенсивности. Предсказанная отражательная способность была ненулевой при всех углах. ^[193]

Третья часть (июль 1821 г.) представляла собой короткий «постскриптум», в котором Френель объявил, что он нашел, с помощью «механического решения», формулу для отражательной способности p- компоненты, которая предсказывала, что отражательная способность равна нулю при угле Брюстера . Таким образом, поляризация отражением была учтена — но с условием, что направление вибрации в модели Френеля было перпендикулярно плоскости поляризации, как определено Малюсом. (О последовавшем споре см. Плоскость поляризации .) Технология того времени не позволяла измерять отражательные способности s и p достаточно точно, чтобы проверить формулы Френеля при произвольных углах падения. Но формулы можно было переписать в терминах того, что мы теперь называем коэффициентом отражения : знаковое отношение отраженной амплитуды к падающей амплитуде. Тогда, если плоскость поляризации падающего луча была под углом 45° к плоскости падения, тангенс соответствующего угла для отраженного луча можно было получить из отношения двух коэффициентов отражения, и этот угол можно было измерить. Френель измерил его для диапазона углов падения, для стекла и воды, и согласие между вычисленными и измеренными углами было лучше, чем 1,5° во всех случаях. ^[194]

Френель подробно изложил «механическое решение» в мемуарах, прочитанных в Академии наук 7 января 1823 года. ^[195] Сохранение энергии было объединено с непрерывностью тангенциальной вибрации на границе раздела. ^[196] Полученные формулы для коэффициентов отражения и отражательной способности стали известны как уравнения Френеля . Коэффициенты отражения для s- и p -поляризаций наиболее кратко выражаются как

r_{s}=-{\frac {\sin(i-r)}{\sin(i+r)}}

r_{p}={\frac {\tan(i-r)}{\tan(i+r)}}\,,

где и — углы падения и преломления; эти уравнения известны соответственно как закон синусов Френеля и закон касательных Френеля . ^[197] Допустив, чтобы коэффициенты были комплексными , Френель даже учел различные фазовые сдвиги s- и p- компонентов из-за полного внутреннего отражения . ^[198] $i$ $r$

Этот успех вдохновил Джеймса МакКуллага и Огюстена-Луи Коши , начиная с 1836 года, на анализ отражения от металлов с использованием уравнений Френеля со сложным показателем преломления . ^[199] Тот же метод применим к неметаллическим непрозрачным средам. С этими обобщениями уравнения Френеля могут предсказывать внешний вид самых разных объектов при освещении, например, в компьютерной графике (см. Физически обоснованный рендеринг ) .

Круговая и эллиптическая поляризация, оптическое вращение (1822)

Правосторонняя/по часовой стрелке циркулярно поляризованная волна, как определено с точки зрения источника. Она будет считаться левосторонней/против часовой стрелки циркулярно поляризованной, если определено с точки зрения приемника. Если вращающийся вектор разложить на горизонтальную и вертикальную составляющие (не показано), они будут на четверть цикла не в фазе друг с другом.

В мемуарах от 9 декабря 1822 года ^[200] Френель ввел термины линейная поляризация (фр. polarisation rectiligne ) для простого случая, в котором перпендикулярные компоненты вибрации находятся в фазе или на 180° вне фазы, круговая поляризация для случая, в котором они имеют одинаковую величину и четверть цикла (±90°) вне фазы, и эллиптическая поляризация для других случаев, в которых два компонента имеют фиксированное отношение амплитуд и фиксированную разность фаз. Затем он объяснил, как оптическое вращение можно понимать как разновидность двойного лучепреломления. Линейно поляризованный свет можно разложить на два кругово поляризованных компонента, вращающихся в противоположных направлениях. Если бы эти компоненты распространялись с немного разными скоростями, разность фаз между ними — и, следовательно, направление их линейно поляризованного результирующего — непрерывно изменялась бы с расстоянием. ^[201]

Эти концепции требовали переопределения различия между поляризованным и неполяризованным светом. До Френеля считалось, что поляризация может изменяться по направлению и степени (например, из-за изменения угла отражения от прозрачного тела), и что она может быть функцией цвета (хроматическая поляризация), но не что она может изменяться по виду . Поэтому считалось, что степень поляризации — это степень, в которой свет может быть подавлен анализатором с соответствующей ориентацией. Свет, преобразованный из линейной в эллиптическую или круговую поляризацию (например, путем прохождения через кристаллическую пластину или путем полного внутреннего отражения), описывался как частично или полностью «деполяризованный» из-за его поведения в анализаторе. После Френеля определяющей чертой поляризованного света было то, что перпендикулярные компоненты вибрации имели фиксированное отношение амплитуд и фиксированную разницу в фазе. Согласно этому определению, эллиптически или кругово поляризованный свет полностью поляризован, хотя он не может быть полностью подавлен одним анализатором. ^[202] Концептуальный разрыв между волновой теорией и селекционизмом снова увеличился.

Полное внутреннее отражение (1817–23)

К 1817 году Брюстером ^[203] , но не было адекватно сообщено ^[204]^[183]^{: 324,} было обнаружено, что плоскополяризованный свет частично деполяризуется полным внутренним отражением, если изначально поляризован под острым углом к плоскости падения. Френель заново открыл этот эффект и исследовал его, включив полное внутреннее отражение в эксперимент по хроматической поляризации. С помощью своей первой теории хроматической поляризации он обнаружил, что явно деполяризованный свет представляет собой смесь компонентов, поляризованных параллельно и перпендикулярно плоскости падения, и что полное отражение вносит разность фаз между ними. ^[205] Выбор подходящего угла падения (еще точно не определен) дал разность фаз в 1/8 цикла (45°). Два таких отражения от «параллельных граней» «двух связанных призм » дали разность фаз в 1/4 цикла (90°). Эти выводы были изложены в мемуаре, представленном в Академию 10 ноября 1817 года и прочитанном две недели спустя. Недатированная заметка на полях указывает, что две соединенные призмы были позже заменены одним «параллелепипедом в стекле», теперь известным как ромб Френеля . ^[206]

Это был мемуар, чье «дополнение» ^[133], датированное январем 1818 года, содержало метод наложения синусоидальных функций и переформулировку закона Малюса в терминах амплитуд. В том же дополнении Френель сообщил о своем открытии, что оптическое вращение можно имитировать, пропуская поляризованный свет через ромб Френеля (все еще в форме «связанных призм»), за которым следует обычная двулучепреломляющая пластина, нарезанная параллельно его оси, с осью в 45° к плоскости отражения ромба Френеля, за которой следует второй ромб Френеля под углом 90° к первому. ^[207] В еще одном мемуаре, зачитанном 30 марта ^[208] , Френель сообщил, что если поляризованный свет был полностью «деполяризован» ромбом Френеля — теперь описываемым как параллелепипед — его свойства не изменялись далее при последующем прохождении через оптически вращающуюся среду или устройство.

Связь между оптическим вращением и двупреломлением была дополнительно объяснена в 1822 году в мемуаре об эллиптической и круговой поляризации. ^[200] За этим последовал мемуар об отражении, прочитанный в январе 1823 года, в котором Френель количественно оценил фазовые сдвиги при полном внутреннем отражении и, следовательно, вычислил точный угол, под которым должен быть разрезан ромб Френеля, чтобы преобразовать линейную поляризацию в круговую. Для показателя преломления 1,51 имелось два решения: около 48,6° и 54,6°. ^[195]^{: 760}

Двойное лучепреломление

Справочная информация: Одноосные и двуосные кристаллы; законы Био

Когда свет проходит через срез кальцита, разрезанный перпендикулярно его оптической оси, разница между временем распространения обыкновенной и необыкновенной волн имеет зависимость второго порядка от угла падения. Если срез наблюдается в сильно сходящемся конусе света, эта зависимость становится значительной, так что эксперимент с хроматической поляризацией покажет картину концентрических колец. Но большинство минералов, наблюдаемых таким образом, показывают более сложную картину колец, включающую два фокуса и лемнискату , как если бы у них были две оптические оси. ^[209]^[210] Два класса минералов естественным образом стали известны как одноосные и двухосные — или, в более поздней литературе, одноосные и двухосные .

В 1813 году Брюстер наблюдал простой концентрический рисунок в « берилле , изумруде , рубине и т. д.». Тот же рисунок позже наблюдали в кальците Волластон , Био и Зеебек . Био, предполагая, что концентрический рисунок был общим случаем, попытался рассчитать цвета с помощью своей теории хроматической поляризации и преуспел в этом лучше для некоторых минералов, чем для других. В 1818 году Брюстер запоздало объяснил, почему: семь из двенадцати минералов, используемых Био, имели лемнискатный рисунок, который Брюстер наблюдал еще в 1812 году; а минералы с более сложными кольцами также имели более сложный закон преломления. ^[211]

В однородном кристалле, согласно теории Гюйгенса, вторичный волновой фронт, который расширяется от начала координат за единицу времени, является поверхностью лучевой скорости — то есть поверхностью, «расстояние» которой от начала координат в любом направлении равно скорости луча в этом направлении. В кальците эта поверхность двухслойная, состоящая из сферы (для обыкновенной волны) и сплющенного сфероида (для необыкновенной волны), которые касаются друг друга в противоположных точках общей оси — касаются на северном и южном полюсах, если использовать географическую аналогию. Но согласно корпускулярной теории двойного преломления Малуса, скорость луча была пропорциональна обратной величине, заданной теорией Гюйгенса, и в этом случае закон скорости имел вид

v_{o}^{2\!}-v_{e}^{2}=k\sin ^{2}\theta \,,

где и были обыкновенной и необыкновенной скоростями луча согласно корпускулярной теории , а был углом между лучом и оптической осью. ^[212] По определению Малуса, плоскость поляризации луча была плоскостью луча и оптической осью, если луч был обыкновенным, или перпендикулярной плоскостью (содержащей луч), если луч был необыкновенным. В модели Френеля направление вибрации было нормальным к плоскости поляризации. Следовательно, для сферы (обыкновенной волны) вибрация была вдоль линий широты (продолжая географическую аналогию); а для сфероида (необыкновенной волны) вибрация была вдоль линий долготы. $v_{o}$ $v_{e}$ $\theta$

29 марта 1819 года ^[213] Био представил мемуары, в которых он предложил простые обобщения правил Малюса для кристалла с двумя осями, и сообщил, что оба обобщения, по-видимому, подтверждаются экспериментом. Для закона скорости квадрат синуса был заменен произведением синусов углов от луча к двум осям ( закон синусов Био ). А для поляризации обычного луча плоскость луча и оси была заменена плоскостью, делящей пополам двугранный угол между двумя плоскостями, каждая из которых содержала луч и одну ось ( закон двугранности Био ). ^[214]^[215] Законы Био означали, что двуосный кристалл с осями под малым углом, расколотый в плоскости этих осей, вел себя почти как одноосный кристалл при почти нормальном падении; это было удачей, поскольку гипс , который использовался в экспериментах по хроматической поляризации, является двуосным. ^[216]

Первые мемуары и дополнения (1821–22)

Пока Френель не обратил свое внимание на двуосное лучепреломление, предполагалось, что одно из двух преломлений было обычным, даже в двуосных кристаллах. ^[217] Но в мемуаре, представленном ^{[Примечание 9]} 19 ноября 1821 года, ^[218] Френель сообщил о двух экспериментах с топазом, показывающих, что ни одно преломление не было обычным в смысле удовлетворения закону Снеллиуса; то есть ни один луч не был продуктом сферических вторичных волн. ^[219]

В том же мемуаре содержалась первая попытка Френеля получить закон двухосной скорости. Для кальцита, если мы поменяем местами экваториальный и полярный радиусы сплющенного сфероида Гюйгенса, сохранив полярное направление, мы получим вытянутый сфероид, касающийся сферы на экваторе. Плоскость, проходящая через центр/начало координат, пересекает этот вытянутый сфероид эллипсом, большая и малая полуоси которого дают величины необыкновенной и обыкновенной лучевых скоростей в направлении, нормальном к плоскости, и (сказал Френель) направления их соответствующих колебаний. Направление оптической оси является нормалью к плоскости, для которой эллипс пересечения сводится к окружности . Таким образом, для двухосного случая Френель просто заменил вытянутый сфероид на трехосный эллипсоид , ^[220] который должен был быть разделен плоскостью таким же образом. В общем, было бы две плоскости, проходящие через центр эллипсоида и разрезающие его по окружности, и нормали к этим плоскостям давали бы две оптические оси. Из геометрии Френель вывел закон синусов Биота (с заменой скоростей лучей на их обратные величины). ^[221]

Эллипсоид действительно дал правильные скорости лучей (хотя первоначальная экспериментальная проверка была лишь приблизительной). Но он не дал правильных направлений колебаний для двуосного случая или даже для одноосного случая, потому что колебания в модели Френеля были касательными к волновому фронту, который для необыкновенного луча, как правило, не является нормальным к лучу. Эта ошибка (которая мала, если, как в большинстве случаев, двупреломление слабое) была исправлена в «выписке», которую Френель прочитал в Академии неделю спустя, 26 ноября. Начиная со сфероида Гюйгенса, Френель получил поверхность 4-й степени, которая при сечении плоскостью, как указано выше, дала бы нормальные к волне скорости для волнового фронта в этой плоскости вместе с их направлениями колебаний. Для двуосного случая он обобщил уравнение, чтобы получить поверхность с тремя неравными главными измерениями; впоследствии он назвал ее «поверхностью упругости». Но он сохранил более ранний эллипсоид в качестве приближения, из которого он вывел двугранный закон Био. ^[222]

Первоначальный вывод Френеля поверхности упругости был чисто геометрическим, а не дедуктивно строгим. Его первая попытка механического вывода, содержащаяся в «дополнении» от 13 января 1822 года, предполагала, что (i) существует три взаимно перпендикулярных направления, в которых смещение производит реакцию в том же направлении, (ii) реакция в противном случае является линейной функцией смещения, и (iii) радиус поверхности в любом направлении является квадратным корнем компонента, в этом направлении , реакции на единичное смещение в этом направлении. Последнее предположение признавало требование, что если волна должна сохранять фиксированное направление распространения и фиксированное направление вибрации, реакция не должна быть вне плоскости этих двух направлений. ^[223]

В том же дополнении Френель рассмотрел, как он мог бы найти для двуосного случая вторичный волновой фронт, который расширяется от начала координат за единицу времени, то есть поверхность, которая сводится к сфере и сфероиду Гюйгенса в одноосном случае. Он отметил, что эта «волновая поверхность» ( surface de l'onde ) ^[224] является касательной ко всем возможным плоским волновым фронтам, которые могли бы пересечь начало координат одну единицу времени назад, и он перечислил математические условия, которым она должна удовлетворять. Но он усомнился в возможности вывода поверхности из этих условий. ^[225]

Во «втором дополнении» ^[226] Френель в конечном итоге использовал два связанных факта: (i) «волновая поверхность» была также поверхностью лучевой скорости, которую можно было получить путем разрезания эллипсоида, который он изначально ошибочно принял за поверхность упругости, и (ii) «волновая поверхность» пересекала каждую плоскость симметрии эллипсоида двумя кривыми: окружностью и эллипсом. Таким образом, он обнаружил, что «волновая поверхность» описывается уравнением 4-й степени

r^{2}{\big (}a^{2}x^{2\!}+b^{2}y^{2\!}+c^{2}z^{2}{\big )}-a^{2}{\big (}b^{2\!}+c^{2}{\big )}x^{2}-b^{2}{\big (}c^{2\!}+a^{2}{\big )}y^{2}-c^{2}{\big (}a^{2\!}+b^{2}{\big )}z^{2}+a^{2}b^{2}c^{2}=\,0\,,

где и - скорости распространения в направлениях, нормальных к осям координат, для колебаний вдоль осей (скорости луча и волны, нормальные в этих особых случаях, одинаковы). ^[227] Более поздние комментаторы ^[228]^{: 19} придали уравнению более компактную и запоминающуюся форму $\,r^{2}=x^{2\!}+y^{2\!}+z^{2},\,$ $\,a,b,c\,$

{\frac {x^{2}}{r^{2}-a^{2}}}+{\frac {y^{2}}{r^{2}-b^{2}}}+{\frac {z^{2}}{r^{2}-c^{2}}}\,=\,1\,.

Ранее во «втором дополнении» Френель смоделировал среду как массив точечных масс и обнаружил, что соотношение силы и смещения описывается симметричной матрицей , подтверждая существование трех взаимно перпендикулярных осей, на которых смещение создает параллельную силу. ^[229] Позже в документе он отметил, что в двуосном кристалле, в отличие от одноосного кристалла, направления, в которых существует только одна нормальная к волне скорость, не совпадают с направлениями, в которых существует только одна лучевая скорость. [ ^230] В настоящее время мы называем первые направления оптическими осями или бинормальными осями, а вторые — лучевыми осями или бирадиальными осями (см. Двулучепреломление ) . ^[231]

«Второе дополнение» Френеля было подписано 31 марта 1822 года и представлено на следующий день — менее чем через год после публикации его гипотезы о чистых поперечных волнах и чуть менее чем через год после демонстрации его прототипа восьмипанельной маячной линзы (см. ниже) .

Вторые мемуары (1822–26)

Представив части своей теории примерно в порядке открытия, Френелю нужно было перегруппировать материал так, чтобы подчеркнуть механические основы; ^[232] и ему все еще требовалась строгая трактовка двугранного закона Био. ^[233] Он уделил внимание этим вопросам в своем «втором мемуаре» о двойном преломлении, ^[234] опубликованном в Recueils of the Académie des Sciences за 1824 год; он был фактически напечатан только в конце 1827 года, через несколько месяцев после его смерти. ^[235] В этой работе, установив три перпендикулярные оси, на которых смещение производит параллельную реакцию, ^[236] и затем построив поверхность упругости, ^[237] он показал, что двугранный закон Био является точным при условии, что бинормали принимаются за оптические оси, а направление нормали к волне — за направление распространения. ^[238]

Еще в 1822 году Френель обсуждал свои перпендикулярные оси с Коши . Признавая влияние Френеля, Коши продолжил разрабатывать первую строгую теорию упругости неизотропных твердых тел (1827), отсюда и первую строгую теорию поперечных волн в ней (1830), которую он сразу же попытался применить к оптике. ^[239] Последовавшие за этим трудности привели к длительным конкурентным усилиям по поиску точной механической модели эфира. ^[240] Собственная модель Френеля не была динамически строгой; например, она выводила реакцию на сдвиговую деформацию, рассматривая смещение одной частицы, в то время как все остальные были фиксированы, и предполагала, что жесткость определяет скорость волны, как в натянутой струне, независимо от направления нормали волны. Но этого было достаточно, чтобы позволить волновой теории сделать то, что не могла селекционистская теория: генерировать проверяемые формулы, охватывающие всеобъемлющий диапазон оптических явлений, из механических предположений. ^[241]

Фотоупругость, эксперименты с несколькими призмами (1822)

В 1815 году Брюстер сообщил, что цвета появляются, когда кусок изотропного материала, помещенный между скрещенными поляризаторами, подвергается механическому напряжению. Сам Брюстер сразу и правильно приписал это явление двулучепреломлению, вызванному напряжением ^[242]^[243], — теперь известному как фотоупругость .

В мемуарах, прочитанных в сентябре 1822 года, Френель объявил, что он подтвердил диагноз Брюстера более непосредственно, сжав комбинацию стеклянных призм так сильно, что через нее можно было увидеть двойное изображение. В своем эксперименте Френель выстроил семь призм 45°–90°–45° , короткой стороной к короткой стороне, с их углами 90°, направленными в чередующихся направлениях. Две полупризмы были добавлены на концах, чтобы сделать всю сборку прямоугольной. Призмы были разделены тонкими пленками скипидара ( тербентина ) для подавления внутренних отражений, что обеспечивало четкую линию зрения вдоль ряда. Когда четыре призмы с одинаковой ориентацией были сжаты в тисках поперек линии зрения, объект, рассматриваемый через сборку, давал два изображения с перпендикулярными поляризациями, с видимым интервалом 1,5 мм на расстоянии одного метра. ^[244]^[245]

В конце этого мемуара Френель предсказал, что если сжатые призмы заменить (ненапряженными) монокристаллическими кварцевыми призмами с совпадающими направлениями оптического вращения, и с их оптическими осями, выровненными вдоль ряда, объект, видимый при взгляде вдоль общей оптической оси, даст два изображения, которые будут казаться неполяризованными при просмотре через анализатор, но при просмотре через ромб Френеля будут поляризованы под углом ±45° к плоскости отражения ромба (что указывает на то, что они изначально были кругово поляризованы в противоположных направлениях). Это напрямую покажет, что оптическое вращение является формой двойного лучепреломления. В мемуаре от декабря 1822 года, в котором он ввел термин круговая поляризация , он сообщил, что подтвердил это предсказание, используя только одну призму 14°–152°–14° и две стеклянные полупризмы. Но он получил более широкое разделение изображений, заменив стеклянную полупризму кварцевыми полупризмами, вращение которых было противоположно вращению призмы 14°–152°–14°. Он добавил мимоходом, что можно было бы еще больше увеличить разделение, увеличив количество призм. ^[246]

Прием

Для дополнения к переводу Риффо « Системы химии » Томсона Френель был выбран для написания статьи о свете. Получившееся 137-страничное эссе под названием « De la Lumière» ( «О свете ») ^[247] было, по-видимому, закончено в июне 1821 года и опубликовано в феврале 1822 года. ^[248] С разделами, охватывающими природу света, дифракцию, тонкопленочную интерференцию, отражение и преломление, двойное преломление и поляризацию, хроматическую поляризацию и изменение поляризации путем отражения, оно сделало всеобъемлющее обоснование волновой теории для читателей, которые не ограничивались физиками. ^[249]

Для изучения первого мемуара Френеля и дополнений к нему по двойному преломлению Академия наук назначила Ампера, Араго, Фурье и Пуассона. ^[250] Их доклад, ^[251] в котором Араго был, несомненно, главным автором, ^[252] был представлен на заседании 19 августа 1822 года. Затем, по словам Эмиля Верде , в переводе Айвора Граттана-Гиннесса :

Сразу после прочтения доклада слово взял Лаплас и... провозгласил исключительную важность только что представленной работы: он поздравил автора с его стойкостью и проницательностью, которые привели его к открытию закона, ускользнувшего от самых умных, и, несколько предвосхищая суждение потомков, заявил, что ставит эти исследования выше всего, что уже давно сообщалось Академии. ^[253]

Неясно, объявлял ли Лаплас о своем переходе в волновую теорию — в возрасте 73 лет. Граттан-Гиннесс поддерживал эту идею. ^[254] Бухвальд, отмечая, что Араго не смог объяснить, что «эллипсоид упругости» не дает правильных плоскостей поляризации, предполагает, что Лаплас мог просто рассматривать теорию Френеля как успешное обобщение закона скорости луча Малюса, охватывающее законы Био. ^[255]

Дифракционная картина Эйри 65 мм от круглой апертуры 0,09 мм, освещенной красным лазерным светом. Размер изображения: 17,3 мм × 13 мм

В следующем году Пуассон, не подписавший отчет Араго, оспаривал возможность существования поперечных волн в эфире. Отталкиваясь от предполагаемых уравнений движения жидкой среды, он отметил, что они не дают правильных результатов для частичного отражения и двойного преломления — как будто это была проблема Френеля, а не его собственная — и что предсказанные волны, даже если они изначально были поперечными, становились более продольными по мере распространения. В ответ Френель заметил, в частности , что уравнения, в которые Пуассон так верил, даже не предсказывали вязкость . Вывод был ясен: учитывая, что поведение света не было удовлетворительно объяснено ничем, кроме поперечных волн, теоретики волн не обязаны отказываться от поперечных волн в угоду предвзятым представлениям об эфире; скорее, разработчик моделей эфира должен был создать модель, которая учитывала бы поперечные волны. ^[256] По словам Роберта Х. Силлимана, Пуассон в конечном итоге принял волновую теорию незадолго до своей смерти в 1840 году. ^[257]

Среди французов нежелание Пуассона было исключением. По словам Эжена Франкеля, «в Париже, кажется, не было никаких дебатов по этому вопросу после 1825 года. Действительно, почти все поколение физиков и математиков, которые достигли зрелости в 1820-х годах — Пуйе, Савар , Ламе , Навье , Лиувилль , Коши — похоже, сразу же приняли эту теорию». Другой известный французский оппонент Френеля, Био, по-видимому, занял нейтральную позицию в 1830 году и в конечном итоге принял волновую теорию — возможно, к 1846 году и, безусловно, к 1858 году. ^[258]

В 1826 году британский астроном Джон Гершель , работавший над книгой-статьей о свете для Encyclopædia Metropolitana , задал Френелю три вопроса относительно двойного преломления, частичного отражения и их связи с поляризацией. Получившаяся статья ^[259] , озаглавленная просто «Свет», была весьма благосклонна к волновой теории, хотя и не совсем свободна от селекционистского языка. Он распространялся частным образом к 1828 году и был опубликован в 1830 году. ^[260] Между тем, перевод Юнга De la Lumière Френеля был опубликован по частям с 1827 по 1829 год. ^[261] Джордж Бидделл Эйри , бывший профессор Лукаса в Кембридже и будущий королевский астроном , безоговорочно принял волновую теорию к 1831 году. ^[262] В 1834 году он, как известно, рассчитал дифракционную картину круглой апертуры из волновой теории, ^[263] тем самым объяснив ограниченное угловое разрешение идеального телескопа (см. Диск Эйри ) . К концу 1830-х годов единственным выдающимся британским физиком, который выступал против волновой теории, был Брюстер , чьи возражения включали сложность объяснения фотохимических эффектов и (по его мнению) дисперсию . ^[264]

Немецкий перевод De la Lumière был опубликован частями в 1825 и 1828 годах. Волновая теория была принята Фраунгофером в начале 1820-х годов и Францем Эрнстом Нейманом в 1830-х годах, а затем начала находить признание в немецких учебниках. ^[265]

Экономия предположений в волновой теории была подчеркнута Уильямом Уэвеллом в его «Истории индуктивных наук », впервые опубликованной в 1837 году. В корпускулярной системе «каждый новый класс фактов требует нового предположения», тогда как в волновой системе гипотеза, разработанная для объяснения одного явления, затем оказывается способной объяснить или предсказать другие. В корпускулярной системе нет «неожиданного успеха, счастливого совпадения, конвергенции принципов из отдаленных мест»; но в волновой системе «все стремится к единству и простоте». ^[266]

Поэтому в 1850 году, когда Фуко и Физо экспериментально обнаружили, что свет распространяется медленнее в воде, чем в воздухе, в соответствии с волновым объяснением рефракции и вопреки корпускулярному объяснению, результат не стал неожиданностью. ^[267]

Маяки и линза Френеля

Френель не был первым человеком, который сфокусировал луч маяка с помощью линзы. Это отличие, по-видимому, принадлежит лондонскому стеклорезу Томасу Роджерсу, чьи первые линзы диаметром 53 см и толщиной 14 см в центре были установлены на старом нижнем маяке в Портленд-Билл в 1789 году. Дальнейшие образцы были установлены примерно в полудюжине других мест к 1804 году. Но большая часть света терялась из-за поглощения в стекле. ^[268]^[269]

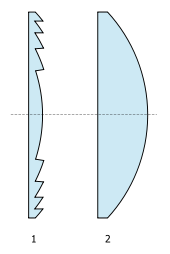
Френель также не был первым, кто предложил заменить выпуклую линзу серией концентрических кольцевых призм, чтобы уменьшить вес и поглощение. В 1748 году граф Бюффон предложил шлифовать такие призмы как ступени в одном куске стекла. ^[4] В 1790 году ^[271] маркиз де Кондорсе предположил, что было бы проще изготавливать кольцевые секции отдельно и собирать их на раме; но даже это было непрактично в то время. ^[272]^[273] Эти конструкции предназначались не для маяков, ^[4] а для зажигательных стекол . ^[274]^{: 609} Брюстер, однако, предложил систему, похожую на систему Кондорсе в 1811 году, ^[4]^[275]^[132] и к 1820 году выступал за ее использование на британских маяках. ^[276]

Между тем, 21 июня 1819 года Френель был «временно» откомандирован Комиссией по маякам (Commission des Phares) по рекомендации Араго (члена Комиссии с 1813 года) для рассмотрения возможных улучшений в освещении маяков. ^[277]^[272] Комиссия была создана Наполеоном в 1811 году и подчинялась Corps des Ponts — работодателю Френеля. ^[278]

К концу августа 1819 года, не зная о предложении Бюффона-Кондорсе-Брюстера, ^[272]^[132] Френель сделал свой первый доклад комиссии, ^[279] рекомендовав то, что он назвал lentilles à échelons (линзы по ступеням) для замены использовавшихся тогда отражателей, которые отражали только около половины падающего света. ^[280]^{[Примечание 10]} Один из собравшихся комиссаров, Жак Шарль , вспомнил предложение Бюффона, оставив Френеля в смущении за то, что он снова «прорвался через открытую дверь». ^[270] Но, в то время как версия Бюффона была двояковыпуклой и цельной, версия Френеля была плосковыпуклой и состояла из нескольких призм для более простой конструкции. Имея официальный бюджет в 500 франков, Френель обратился к трем производителям. Третий, Франсуа Солей, изготовил прототип. Завершенный в марте 1820 года, он имел квадратную линзовую панель размером 55 см на стороне, содержащую 97 многоугольных (не кольцевых) призм, и настолько впечатлил Комиссию, что Френелю было предложено сделать полную версию из восьми панелей. Эта модель, завершенная годом позже, несмотря на недостаточное финансирование, имела панели размером 76 см в квадрате. На публичном представлении вечером 13 апреля 1821 года она была продемонстрирована в сравнении с новейшими рефлекторами, которые она внезапно сделала устаревшими. ^[281]

Следующая линза Френеля представляла собой вращающийся аппарат с восемью панелями «бычий глаз», изготовленными в виде кольцевых дуг компанией Saint-Gobain , ^[273] давая восемь вращающихся лучей, которые моряки могли видеть как периодическую вспышку. Над и позади каждой основной панели находилась меньшая наклонная панель «бычий глаз» трапециевидного контура с трапециевидными элементами. ^[282] Она преломляла свет в наклонное плоское зеркало, которое затем отражало его горизонтально, на 7 градусов впереди основного луча, увеличивая продолжительность вспышки. ^[283] Под основными панелями находились 128 маленьких зеркал, расположенных в четырех кольцах, сложенных друг на друга, как планки жалюзи или жалюзи. Каждое кольцо, имеющее форму усеченного конуса , отражало свет к горизонту , давая более слабый устойчивый свет между вспышками. Официальное испытание, проведенное на незаконченной Триумфальной арке 20 августа 1822 года, было засвидетельствовано комиссией, а также Людовиком XVIII и его окружением, с расстояния в 32 км. Аппарат был оставлен на зиму в Бордо , а затем собран на маяке Кордуан под наблюдением Френеля. 25 июля 1823 года была зажжена первая в мире линза Френеля для маяка. ^[284] Вскоре после этого Френель начал кашлять кровью. ^[285]

В мае 1824 года ^[132] Френель был повышен до секретаря Комиссии по Фаресу , став первым членом этого органа, получающим зарплату, ^[286] хотя и в параллельной роли главного инженера. ^[287] Он также был экзаменатором (не преподавателем) в Политехнической школе с 1821 года; но плохое здоровье, долгие часы работы во время экзаменационного сезона и беспокойство по поводу осуждения других побудили его уйти с этой должности в конце 1824 года, чтобы сберечь силы для работы на маяке. ^[34]^[288]

В том же году он спроектировал первую фиксированную линзу — для равномерного распределения света по горизонту, минимизируя потери сверху или снизу. ^[272] В идеале изогнутые преломляющие поверхности должны были быть сегментами тороидов вокруг общей вертикальной оси, так что диоптрическая панель выглядела бы как цилиндрический барабан. Если бы это было дополнено отражающими ( катоптрическими ) кольцами выше и ниже преломляющих (диоптрических) частей, весь аппарат выглядел бы как улей. ^[289] Вторая линза Френеля, которая поступила на вооружение, действительно была фиксированной линзой третьего порядка, установленной в Дюнкерке 1 февраля 1825 года. ^[290] Однако из-за сложности изготовления больших тороидальных призм этот аппарат имел 16-сторонний многоугольный план. ^[291]

В 1825 году Френель расширил конструкцию фиксированной линзы, добавив вращающуюся решетку за пределами фиксированной решетки. Каждая панель вращающейся решетки должна была преломлять часть фиксированного света от горизонтального веера в узкий луч. ^[272]^[292]

Также в 1825 году Френель представил Carte des Phares (Карту маяков), в которой предусматривалась система из 51 маяка и более мелких портовых огней в иерархии размеров линз (называемых порядками , первый порядок является самым большим), с различными характеристиками для облегчения распознавания: постоянный свет (от неподвижной линзы), одна вспышка в минуту (от вращающейся линзы с восемью панелями) и две вспышки в минуту (шестнадцать панелей). ^[293]

Вращающаяся катадиоптрическая линза Френеля первого порядка, датированная 1870 годом, экспонируется в *Национальном морском музее* в Париже. В этом случае диоптрические призмы (внутри бронзовых колец) и катадиоптрические призмы (снаружи) расположены так, чтобы давать чисто мигающий свет с четырьмя вспышками за один оборот. Сборка имеет высоту 2,54 метра и весит около 1,5 тонны.

В конце 1825 года ^[294] для уменьшения потерь света в отражающих элементах Френель предложил заменить каждое зеркало катадиоптрической призмой, через которую свет проходил бы путем преломления через первую поверхность, затем полного внутреннего отражения от второй поверхности, затем преломления через третью поверхность. ^[295] Результатом стала линза маяка, какой мы ее знаем сейчас. В 1826 году он собрал небольшую модель для использования на канале Сен-Мартен , ^[296] но он не дожил до полноразмерной версии.

Первая фиксированная линза с тороидальными призмами была аппаратом первого порядка, разработанным шотландским инженером Аланом Стивенсоном под руководством Леонора Френеля и изготовленным Айзеком Куксоном и компанией Co. из французского стекла; он вступил в эксплуатацию на острове Мей в 1836 году. ^[297] Первые большие катадиоптрические линзы были фиксированными линзами третьего порядка, изготовленными в 1842 году для маяков в Гравелине и Иль-Вьерж . Первая полностью катадиоптрическая линза первого порядка , установленная в Айи в 1852 году, давала восемь вращающихся лучей, которым помогали восемь катадиоптрических панелей наверху (для удлинения вспышек), а также фиксированный свет снизу. Первая полностью катадиоптрическая линза с чисто вращающимися лучами — также первого порядка — была установлена в Сен-Клеман-де-Бален в 1854 году и ознаменовала завершение оригинальной Carte des Phares Огюстена Френеля . ^[298]

Производство цельных ступенчатых диоптрических линз — примерно таких, как предполагал Бюффон — стало практичным в 1852 году, когда Джон Л. Джиллиленд из компании Brooklyn Flint-Glass Company запатентовал метод изготовления таких линз из прессованного стекла. ^[299] К 1950-м годам замена стекла пластиком сделала экономичным использование мелкоступенчатых линз Френеля в качестве конденсаторов в диапроекторах . ^[300] Еще более мелкие ступени можно найти в недорогих пластиковых «листовых» увеличительных устройствах .

Почести

Френель был избран в Общество филоматики Парижа в апреле 1819 года ^{[301] , а в 1822 году стал одним из редакторов}«Бюллетеня наук» Общества . ^[302] Еще в мае 1817 года по предложению Араго Френель подал заявку на членство в Академии наук, но получил только один голос. ^[301] Успешным кандидатом на тот раз стал Жозеф Фурье. В ноябре 1822 года повышение Фурье до постоянного секретаря Академии создало вакансию в секции физики, которую в феврале 1823 года занял Пьер Луи Дюлонг с 36 голосами против 20 у Френеля. Но в мае 1823 года, после того как из-за смерти Жака Шарля образовалась еще одна вакансия , избрание Френеля было единогласным. ^[303] В 1824 году, ^[304] Френель был удостоен звания кавалера Почетного легиона (Рыцаря Почетного легиона ). ^[9]

Тем временем в Британии волновая теория еще не получила распространения; в ноябре 1824 года Френель написал Томасу Юнгу следующее письмо:

Я далек от того, чтобы отрицать ценность, которую я придаю похвалам английских ученых, или притворяться, что они не польстили бы мне приятно. Но в течение долгого времени эта чувствительность, или тщеславие, которое называется любовью к славе, было во мне значительно притуплено: я работаю гораздо меньше, чтобы завоевать голоса публики, чем чтобы получить внутреннее одобрение, которое всегда было самой сладкой наградой за мои усилия. Несомненно, мне часто требовалось жало тщеславия, чтобы побудить меня продолжать мои исследования в моменты отвращения или уныния; но все комплименты, которые я получал от ММ. Араго, Лапласа и Биота, никогда не доставляли мне такого удовольствия, как открытие теоретической истины и подтверждение моих расчетов экспериментом. ^[305]

Но вскоре последовала «похвала английских учёных». 9 июня 1825 года Френель был избран иностранным членом Лондонского королевского общества . ^[306] В 1827 году ^[25]^[307] он был награждён медалью Румфорда за 1824 год «За разработку волновой теории в применении к явлениям поляризованного света и за различные важные открытия в области физической оптики». ^[308]

Памятник Френелю на его родине ^[7]^[10] (см. выше) был открыт 14 сентября 1884 года ^[8] речью Жюля Жамина , постоянного секретаря Академии наук. ^[9]^[309] « ФРЕСНЕЛЬ » входит в число 72 имен, выбитых на Эйфелевой башне (на юго-восточной стороне, четвертое слева). В 19 веке, когда каждый маяк во Франции обзавелся линзой Френеля, каждый из них обзавелся бюстом Френеля, по-видимому, наблюдающим за береговой линией, которую он сделал более безопасной. ^[310] Лунные особенности Promontorium Fresnel и Rimae Fresnel позже были названы в его честь. ^[311]

Упадок и смерть

Здоровье Френеля, которое всегда было слабым, ухудшилось зимой 1822–1823 годов, что увеличило срочность его оригинального исследования и (отчасти) помешало ему написать статью о поляризации и двойном преломлении для Encyclopaedia Britannica . ^[312] Мемуары о круговой и эллиптической поляризации и оптическом вращении, ^[200] и о подробном выводе уравнений Френеля и их применении к полному внутреннему отражению, ^[195] датируются этим периодом. Весной он достаточно поправился, по его собственному мнению, чтобы руководить установкой линз в Кордуане. Вскоре после этого стало ясно, что его заболеванием был туберкулез . ^[285]

В 1824 году ему посоветовали, что если он хочет прожить дольше, ему нужно сократить свою деятельность. Понимая, что работа на маяке является его самой важной обязанностью, он ушел с должности экзаменатора в Политехнической школе и закрыл свои научные тетради. Его последняя записка в Академию, прочитанная 13 июня 1825 года, описывала первый радиометр и приписывала наблюдаемую силу отталкивания разнице температур. ^[313] Хотя его фундаментальные исследования прекратились, его пропаганда не прекратилась; еще в августе или сентябре 1826 года он нашел время, чтобы ответить на вопросы Гершеля о волновой теории. ^[314] Именно Гершель рекомендовал Френеля к медали Румфорда Королевского общества. ^[315]

Кашель Френеля обострился зимой 1826–1827 годов, и он был слишком болен, чтобы вернуться в Матье весной. Заседание Академии 30 апреля 1827 года было последним, на котором он присутствовал. В начале июня его отвезли в Виль-д'Авре , в 12 километрах (7,5 миль) к западу от Парижа. Там к нему присоединилась его мать. 6 июля прибыл Араго, чтобы вручить медаль Румфорда. Почувствовав горе Араго, Френель прошептал, что «самая красивая корона мало что значит, когда ее кладут на могилу друга». У Френеля не было сил ответить Королевскому обществу. Он умер восемь дней спустя, в День взятия Бастилии . ^[316]

Он похоронен на кладбище Пер-Лашез в Париже. Надпись на его надгробии частично стерта; разборчивая часть гласит: «Памяти Огюстена Жана Френеля, члена Института Франции ».

Посмертные публикации

«Вторые мемуары» Френеля о двойном преломлении ^[234] были напечатаны лишь в конце 1827 года, через несколько месяцев после его смерти. ^[317] До этого времени лучшим опубликованным источником по его работе о двойном преломлении был отрывок из этого мемуара, напечатанный в 1822 году. ^[318] Его окончательный труд о частичном отражении и полном внутреннем отражении, ^[195] прочитанный в Академии в январе 1823 года, считался утерянным, пока не был вновь обнаружен среди бумаг покойного Жозефа Фурье (1768–1830) и напечатан в 1831 году. До этого времени он был известен в основном по отрывку, напечатанному в 1823 и 1825 годах. Мемуар, вводящий параллелепипедную форму ромба Френеля, ^[319] прочитанный в марте 1818 года, был утерян до 1846 года, ^[320] а затем вызвал такой интерес, что вскоре был переиздан на английском языке. ^[321] Большинство трудов Френеля о поляризованном свете до 1821 года, включая его первую теорию хроматической поляризации (представленную 7 октября 1816 года) и решающее «дополнение» от января 1818 года ^[133] , не были опубликованы полностью до тех пор, пока его Oeuvres complètes («полное собрание сочинений») не начали появляться в 1866 году. ^[322] «Дополнение» от июля 1816 года, предлагающее «эффективный луч» и сообщающее о знаменитом эксперименте с двойным зеркалом, постигла та же участь, ^[323] что и «первые мемуары» о двойном преломлении. ^[324]

Публикация собраний сочинений Френеля сама по себе была отложена из-за смерти последующих редакторов. Первоначально эта задача была поручена Феликсу Савари , который умер в 1841 году. Она была возобновлена двадцать лет спустя Министерством народного просвещения. Из трех редакторов, в конечном итоге названных в Oeuvres , Сенармон умер в 1862 году, Верде в 1866 году и Леонор Френель в 1869 году, к тому времени вышли только два из трех томов. ^[325] В начале тома 3 (1870) завершение проекта описано в длинной сноске « Ж. Лиссажу ».

В Oeuvres ^[326] не включены две короткие заметки Френеля о магнетизме, которые были обнаружены среди рукописей Ампера. ^[327]^{: 104} В ответ на открытие Эрстедом электромагнетизма в 1820 году Ампер изначально предположил, что поле постоянного магнита было вызвано макроскопическим циркулирующим током . Френель предположил вместо этого, что вокруг каждой частицы магнита циркулирует микроскопический ток. В своей первой заметке он утверждал, что микроскопические токи, в отличие от макроскопических токов, объясняют, почему полый цилиндрический магнит не теряет свой магнетизм при продольном разрезе. Во второй заметке, датированной 5 июля 1821 года, он далее утверждал, что макроскопический ток имеет контрфактуальное следствие, что постоянный магнит должен быть горячим, тогда как микроскопические токи, циркулирующие вокруг молекул, могут избежать механизма нагрева. ^[327]^{: 101–104} Он не должен был знать, что фундаментальные единицы постоянного магнетизма даже меньше молекул (см. Электронный магнитный момент ) . Две заметки, вместе с признанием Ампера, были в конечном итоге опубликованы в 1885 году. ^[328]

Утраченные работы

Эссе Френеля Rêveries 1814 года не сохранилось. ^[329] Статья "Sur les Différents Systèmes relatifs à la Théorie de la Lumière" ("О различных системах, относящихся к теории света"), которую Френель написал для недавно созданного английского журнала European Review , ^[330] была получена агентом издательства в Париже в сентябре 1824 года. Журнал потерпел неудачу до того, как статья Френеля была опубликована. Френель безуспешно пытался вернуть рукопись. Редакторы его собрания сочинений не смогли ее найти и пришли к выводу, что она, вероятно, была утеряна. ^[331]

Незаконченная работа

Эфирное сопротивление и плотность эфира

В 1810 году Араго экспериментально обнаружил, что степень преломления звездного света не зависит от направления движения Земли относительно луча зрения. В 1818 году Френель показал, что этот результат можно объяснить волновой теорией ^[332], исходя из гипотезы, что если объект с показателем преломления движется со скоростью относительно внешнего эфира (принятого за неподвижный), то скорость света внутри объекта приобретает дополнительную составляющую . Он поддержал эту гипотезу, предположив, что если плотность внешнего эфира принять за единицу, то плотность внутреннего эфира будет , избыток которой, а именно , увлекается со скоростью , откуда средняя скорость внутреннего эфира будет . Множитель в скобках, который Френель первоначально выразил в терминах длин волн, ^[333] стал известен как коэффициент сопротивления Френеля . (См. Гипотеза сопротивления эфира .) $n$ $v$ $\,v(1-1/n^{2})$ $n^{2}$ $\,n^{2}{-}1\,$ $v$ $\,v(1-1/n^{2})$

В своем анализе двойного преломления Френель предположил, что различные показатели преломления в разных направлениях в пределах одной и той же среды были обусловлены направленным изменением упругости, а не плотности (потому что концепция массы на единицу объема не является направленной). Но в своем рассмотрении частичного отражения он предположил, что различные показатели преломления различных сред были обусловлены различной плотностью эфира, а не различной упругостью. ^[334]

Дисперсия

Аналогия между световыми волнами и поперечными волнами в упругих твердых телах не предсказывает дисперсию — то есть частотную зависимость скорости распространения, которая позволяет призмам создавать спектры и заставляет линзы страдать от хроматической аберрации . Френель в De la Lumière и во втором дополнении к своему первому мемуару о двойном преломлении предположил, что дисперсию можно объяснить, если частицы среды оказывают силы друг на друга на расстояниях, которые составляют значительные доли длины волны. ^[335] Позднее, не раз, Френель ссылался на демонстрацию этого результата как на содержащуюся в примечании, приложенном к его «второму мемуару» о двойном преломлении. ^[336] Такая заметка не появилась в печати, и соответствующие рукописи, найденные после его смерти, показали только, что около 1824 года он сравнивал показатели преломления (измеренные Фраунгофером) с теоретической формулой, значение которой не было полностью объяснено. ^[337]

В 1830-х годах предположение Френеля было подхвачено Коши, Баденом Пауэллом и Филиппом Келландом , и было обнаружено, что оно вполне согласуется с изменением показателей преломления в зависимости от длины волны в видимом спектре для различных прозрачных сред (см. уравнение Коши ) . ^[338] Этих исследований было достаточно, чтобы показать, что волновая теория по крайней мере совместима с дисперсией; если модель дисперсии должна была быть точной в более широком диапазоне частот, ее необходимо было модифицировать, чтобы учесть резонансы внутри среды (см. уравнение Селлмейера ) . ^[339]

Коническая рефракция

Аналитическая сложность вывода Френелем поверхности лучевой скорости была неявным вызовом для поиска более короткого пути к результату. На это ответили МакКуллах в 1830 году и Уильям Роуэн Гамильтон в 1832 году. ^[340]^[341]^[342]

Наследие

Фонарная комната маяка Кордуан , в которой в 1823 году была введена в эксплуатацию первая линза Френеля. Современная фиксированная катадиоптрическая линза «улей» заменила оригинальную вращающуюся линзу Френеля в 1854 году. ^[343]

В течение столетия после первоначального предложения Френеля о ступенчатой линзе более 10 000 светильников с линзами Френеля защищали жизни и имущество по всему миру. ^[344] Что касается других преимуществ, историк науки Тереза Х. Левитт заметила:

Куда бы я ни посмотрел, история повторялась. Момент, когда линза Френеля появлялась в каком-то месте, был моментом, когда этот регион становился связанным с мировой экономикой. ^[345]

В истории физической оптики успешное возрождение волновой теории Френелем выдвигает его на роль центральной фигуры между Ньютоном, который считал, что свет состоит из корпускул, и Джеймсом Клерком Максвеллом , который установил, что световые волны являются электромагнитными. В то время как Альберт Эйнштейн описал работу Максвелла как «самую глубокую и самую плодотворную, которую физика пережила со времен Ньютона», ^[346] комментаторы эпохи между Френелем и Максвеллом сделали аналогичные сильные заявления о Френеле:

МакКуллах еще в 1830 году писал, что механическая теория двойного преломления Френеля «сделала бы честь проницательности Ньютона». ^[341]^{: 78}
Ллойд в своем отчете о прогрессе и современном состоянии физической оптики (1834) для Британской ассоциации содействия развитию науки проанализировал предыдущие знания о двойном преломлении и заявил:
Теория Френеля, к которой я сейчас перехожу, и которая не только охватывает все известные явления, но даже превзошла наблюдения и предсказала следствия, которые впоследствии были полностью проверены, — я убежден, будет считаться лучшим обобщением в физической науке, которое было сделано со времени открытия всемирного тяготения. ^[347]
В 1841 году Ллойд опубликовал свои «Лекции по волновой теории света », в которых он описал теорию поперечных волн Френеля как «самое благородное полотно, когда-либо украшавшее область физической науки, за исключением только системы Вселенной Ньютона» ^{[6] .}
Уильям Уэвелл во всех трех изданиях своей «Истории индуктивных наук» (1837, 1847 и 1857) в конце книги IX сравнил историю физической астрономии и физической оптики и пришел к следующему выводу:
Было бы, пожалуй, слишком причудливо пытаться установить параллелизм между выдающимися личностями, которые фигурируют в этих двух историях. Если бы мы сделали это, мы должны были бы считать Гюйгенса и Гука стоящими на месте Коперника , поскольку, как и он, они объявили истинную теорию, но оставили ее развитие и механическое подтверждение будущему веку; Малус и Брюстер, объединяя их вместе, соответствуют Тихо Браге и Кеплеру , трудолюбивым в накоплении наблюдений, изобретательным и счастливым в открытии законов явлений; а Юнг и Френель вместе составляют Ньютона оптической науки. ^[348]

То, что Уэвелл называл «истинной теорией», с тех пор претерпело два крупных пересмотра. Первый, сделанный Максвеллом, определил физические поля, вариации которых составляют волны света. Не имея преимуществ от этих знаний, Френель сумел построить первую в мире когерентную теорию света, показав в ретроспективе, что его методы применимы к нескольким типам волн. Второй пересмотр, инициированный объяснением Эйнштейна фотоэлектрического эффекта , предполагал, что энергия световых волн делится на кванты , которые в конечном итоге были отождествлены с частицами, называемыми фотонами . Но фотоны не совсем соответствовали корпускулам Ньютона; например, объяснение Ньютоном обычной рефракции требовало, чтобы корпускулы двигались быстрее в средах с более высоким показателем преломления, чего не делают фотоны. Фотоны также не вытесняли волны; скорее, они привели к парадоксу дуализма волна-частица . Более того, явления, изученные Френелем, которые включали почти все оптические явления, известные в его время, по-прежнему проще всего объяснить в терминах волновой природы света. Таким образом, ещё в 1927 году астроном Эжен Мишель Антониади объявил Френеля «доминирующей фигурой в оптике».  ^[349]

Смотрите также

Пояснительные записки

^ Английское произношение варьируется: / ˈ f r eɪ n ɛ l , - n əl / FRAY -nel, -⁠nəl , или / ˈ f r ɛ n ɛ l , - əl / FREN -el, -⁠əl , или / f r eɪ ˈ n ɛ l / fray- НЭЛ . ^[1] Французский: [oɡystɛ̃ ʒɑ̃ fʁɛnɛl] ; ^[2]
^ Ньютон (1730) наблюдал, как перья действуют как отражательные решетки и как пропускающие решетки, но классифицировал первый случай как тонкие пластины (стр. 252), а второй, более неопределенно, как перегиб (стр. 322). Оглядываясь назад, последний эксперимент (стр. 322, конец Obs. 2) опасен для зрения и не должен повторяться в том виде, в котором он написан.
↑ История о том, что Ампер потерял эссе (взятая из Boutry, 1948, стр. 593?), неявно противоречит Darrigol (2012, стр. 198), Buchwald (1989, стр. 117), письмо Мериме Френелю от 20 декабря 1814 года (во Fresnel, 1866–70, т. 2, стр. 830–831) и две сноски в собрании сочинений Френеля (Fresnel, 1866–70, т. 1, стр. xxix–xxx, примечание 4 и стр. 6n).
^ "Книга Юнга", которую Френель отличал от Philosophical Transactions , предположительно, является A Course of Lectures on Natural Philosophy and the Mechanical Arts (2 тома, 1807). В томе 1 соответствующие иллюстрации - это Plate XX (на стр. 777), включая знаменитую картину интерференции с двумя источниками (рис. 267), и Plate XXX (на стр. 787), включая гиперболические пути полос в этой картине (рис. 442), за которыми следуют наброски других картин дифракции и картин тонкой пластины, без визуальных намеков на их физические причины. В томе 2, который включает лекции Бейкера из Philosophical Transactions , на рис. 108 (стр. 632) показан только один случай неотклоненного прямого луча, пересекающего отраженный луч.
^ Силлиман (1967, стр. 163) и Франкель (1976, стр. 156) датируют заметку Араго о сцинтилляции 1814 годом; но последовательность событий подразумевает 1816 год, что согласуется с Дарриголом (2012, стр. 201, ‍ 290 ). Кипнис (1991, стр. 202–203, 206) доказывает более позднюю дату и объясняет происхождение и распространение неправильной более ранней даты.
^ В той же части Френель признал письмо Юнга Араго, датированное 29 апреля 1818 года (и утерянное до 1866 года), в котором Юнг предположил, что световые волны могут быть аналогичны волнам на натянутых струнах. Но Френель был недоволен аналогией, поскольку она предполагала как поперечные, так и продольные режимы распространения и ее было трудно согласовать с жидкой средой (Silliman, 1967, стр. 214–215; Fresnel, 1821a, §13).
^ Френель, пытаясь показать, что поперечные волны не абсурдны, предположил, что эфир представляет собой жидкость, состоящую из решетки молекул, соседние слои которой будут сопротивляться скользящему смещению до определенной точки, за которой они будут тяготеть к новому равновесию. Такая среда, как он думал, будет вести себя как твердое тело при достаточно малых деформациях, но как идеальная жидкость при больших деформациях. Что касается отсутствия продольных волн, он далее предположил, что слои оказывают несравненно большее сопротивление изменению расстояния, чем скользящему движению (Silliman, 1967, стр. 216–218; Fresnel, 1821a, §§ 11–12; ср. Fresnel, 1827, tr. Hobson, стр. 258–262).
^ Буква s изначально происходит от немецкого senkrecht , что означает перпендикулярно (к плоскости падения).
^ В собрании сочинений Френеля (1866–70) говорится, что статья была «представлена» (« présenté »), если она была просто доставлена Постоянному секретарю Академии для засвидетельствования или обработки (ср. т. 1, стр. 487; т. 2, стр. 261, ‍ 308 ). В таких случаях в этой статье предпочтительнее использовать общее слово «представлен», чтобы избежать впечатления, что статья прошла формальное прочтение.
^ Другой отчет Френеля, датированный 29 августа 1819 года (Fresnel, 1866–70, т. 3, стр. 15–21), касается испытаний рефлекторов и не упоминает ступенчатые линзы, за исключением несвязанного наброска на последней странице рукописи. Протоколы заседаний Комиссии восходят только к 1824 году, когда сам Френель занял пост секретаря (Fresnel, 1866–70, т. 3, стр. 6n). Таким образом, к сожалению, невозможно установить точную дату, когда Френель официально рекомендовал lentilles à échelons .

Ссылки

Цитаты

^ Дж. Уэллс (2008), Словарь произношения Лонгмана (3-е изд.), Pearson Longman, ISBN 978-1-4058-8118-0.
^ «Френель», Словарь английского языка Коллинза / Новый всемирный словарь колледжа Вебстера .
^ Дарригол, 2012, стр. 220–223.
^ abcd Чисхолм, Хью , ред. (1911), «Маяк» , Encyclopaedia Britannica , т. 16 (11-е изд.), Cambridge University Press, стр. 627–651.
^ Дарригол, 2012, стр. 205.
^ ab H. Lloyd, Lectures on the Wave-theory of Light, Dublin: Milliken, 1841, Part II , Lecture III , p. 26. То же самое описание было сохранено во «втором издании», опубликованном под названием Elementary Treatise on the Wave-theory of Light (London: Longman, Brown, Green, Longmans, & Roberts, 1857; p. 136), и в «третьем издании» (London: Longmans, Green, & Co., 1873; p. 167), которое появилось в том же году, что и « Трактат об электричестве и магнетизме» Максвелла .
^ abcd 'martan' (автор), "Eure (27)", Guide National des Maisons Natales , 30 мая 2014 г.
^ ab Bibliothèques et Médiathèque, «Инаугурация Бройля, 14 сентября 1884 года, бюст Огюстена Френеля», архивировано 28 июля 2018 года.
^ abc Académie des Sciences, «Augustin Fresnel», доступ 21 августа 2017 г.; архив 15 февраля 2017 г.
^ аб Д. Перше, «Памятник Огюстену Френелю – Бройлю», e-monumen.net , 5 июля 2011 г.
^ ab JH Favre, «Augustin Fresnel», geneanet.org , дата обращения 30 августа 2017 г.
^ abc 'jeanelie' (автор), "Augustine Charlotte Marie Louise Merimee" и "Louis Jacques Fresnel", geneanet.org , дата обращения 30 августа 2017 г.
^ Левитт (2013, стр. 23) говорит «в 1790 году». Силлиман (1967, стр. 7) говорит «к 1790 году». Бутри (1948, стр. 590) говорит, что семья покинула Бройль в 1789 году.
^ ab Silliman, 2008, стр. 166.
↑ Бутри, 1948, стр. 590.
^ Левитт, 2013, стр. 99.
↑ Френель, 1866–70.
^ Левитт, 2013, стр. 72.
^ аб Пилле, Морис (1881–1964) (1922). L'expédition scientifique et artique de Mésopotamie et de Médie, 1851–1855 (на французском языке). Доступ из Галлики – Национальная библиотека Франции: Libraire Ancienne Honoré Champion.{{cite book}}: CS1 maint: numeric names: authors list (link)
^ Левитт, 2009, стр. 49.
^ Левитт, 2013, стр. 24–25; Бухвальд, 1989, стр. 111.
^ Этот возраст был указан Араго в его элегии (Arago, 1857, стр. 402) и широко распространен ( Encyclopaedia Britannica , 1911; Buchwald, 1989, стр. 111; Levitt, 2013, стр. 24; и т. д.). Но переиздание элегии в конце собрания сочинений Френеля имеет сноску, предположительно Леонора Френеля, в которой говорится, что «восемь» должно быть «пять или шесть», и выражается сожаление «о спешке, с которой нам пришлось собирать заметки, которые были запоздало запрошены для биографической части этой речи» (Fresnel, 1866–70, т. 3, стр. 477n). Силлиман (1967, стр. 9n) принимает исправление.
^ Левитт, 2013, стр. 25; Араго, 1857, стр. 402; Бутри, 1948, стр. 590–591.
^ Левитт, 2013, стр. 25–26; Силлиман, 1967, стр. 9–11.
^ ab Chisholm, Hugh , ed. (1911), "Fresnel, Augustin Jean" , Encyclopaedia Britannica , т. 11 (11-е изд.), Cambridge University Press, стр. 209.
↑ Бутри, 1948, стр. 592.
^ Silliman, 1967, стр. 14; Arago, 1857, стр. 403. Решение Френеля было напечатано в Correspondance sur l'École polytechnique , № 4 (июнь–июль 1805 г.), стр. 78–80, и перепечатано в Fresnel, 1866–70, т. 2, стр. 681–684. Бутри (1948, стр. 591) считает эту историю относящейся к вступительному экзамену.
^ Левитт, 2013, стр. 26–27; Силлиман, 2008, стр. 166; Бутри, 1948, стр. 592, 601.
↑ Kneller, tr. Kettle, 1911, стр. 147. Kneller интерпретирует цитату как относящуюся к Августину; но Verdet (in Fresnel, 1866–70, vol. 1, pp. xcviii–xcix), цитируемый Silliman (1967, p. 8), дает ей другой контекст, ссылаясь на академические успехи Луи.
^ Левитт, 2013, стр. 24.
↑ Кнеллер, 1911, стр. 148.
^ Кнеллер, 1911, стр. 148–149n; ср. Араго, 1857, с. 470.
^ Граттан-Гиннесс, 1990, стр. 914–915.
^ abc HM Brock, «Френель, Огюстен-Жан», Католическая энциклопедия , 1907–12, т. 6 (1909).
^ Френель, 1866–70, том. 1, с. xcvii.
^ Рейли, Д. (декабрь 1951 г.). «Соли, кислоты и щелочи в 19 веке; сравнение достижений во Франции, Англии и Германии». Isis; международный обзор, посвященный истории науки и ее культурным влияниям . 42 (130): 287–296. doi :10.1086/349348. ISSN 0021-1753. PMID 14888349.
^ Cf. Silliman, 1967, стр. 28–33; Levitt, 2013, стр. 29; Buchwald, 1989, стр. 113–114. Сохранившаяся переписка по кальцинированной соде охватывает период с августа 1811 по апрель 1812 года; см. Fresnel, 1866–70, т. 2, стр. 810–817.
↑ Бутри, 1948, стр. 593–594.
↑ Френель, 1866–70, т. 2, стр. 819; выделено в оригинале.
↑ Бутри, 1948, стр. 593; Араго, 1857, стр. 407–408; Френель, 1815a.
↑ Académie des Sciences, «История Французской академии наук», по состоянию на 8 декабря 2017 г.; в архиве 13 августа 2017 г.
^ Араго, 1857, стр. 405; Силлиман, 2008, стр. 166. Араго не использует кавычки.
^ Левитт, 2013, стр. 38–39; Бутри, 1948, стр. 594; Араго, 1857, стр. 405–406; Кипнис, 1991, стр. 167.
↑ Гюйгенс, 1690, пер. Томпсона, стр. 20–21.
↑ Ньютон, 1730, стр. 362.
↑ Гюйгенс, 1690, пер. Томпсона, стр. 22–38.
^ Дарригол, 2012, стр. 93–94, 103.
^ Дарригол, 2012, стр. 129–130, 258.
↑ Гюйгенс, 1690, пер. Томпсона, стр. 52–105.
^ de Witte, AJ (1 мая 1959 г.). «Эквивалентность принципа Гюйгенса и принципа Ферма в лучевой геометрии». American Journal of Physics . 27 (5): 293–301. Bibcode : 1959AmJPh..27..293D. doi : 10.1119/1.1934839. ISSN 0002-9505.Исправление : На рис. 7(б) каждый экземпляр «луча» должен быть «нормальным» (отмечено в т. 27, № 6, стр. 387).
↑ Янг, 1855, стр. 225–226, 229.
^ Дарригол, 2012, стр. 62–64.
^ Дарригол, 2012, стр. 87.
↑ Ньютон, Исаак (18 ноября 1672 г.). «Ответ г-на Исаака Ньютона на некоторые соображения по поводу его учения о свете и цветах; каковое учение было напечатано в Числах 80 этих трактатов». Философские труды Лондонского королевского общества . 7 (88): 5084–5103. doi :10.1098/rstl.1672.0051. ISSN 0261-0523. JSTOR 100964 .
^ Дарригол, 2012, стр. 53–56.
↑ Гюйгенс, 1690, пер. Томпсона, стр. 17.
^ Дарригол, 2012, стр. 98–100; Ньютон, 1730, с. 281.
↑ Ньютон, 1730, стр. 284.
↑ Ньютон, 1730, стр. 283, ‍ 287 .
^ ab N. Kipnis, «Физическая оптика», в I. Grattan-Guinness (ред.), Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences , JHU Press, 2003, т. 2, стр. 1143–1152.
↑ Ньютон, 1730, стр. 279, 281–282.
^ abcde Т. Янг, «О теории света и цветов» (Бейкерианская лекция), Philosophical Transactions of the Royal Society , т. 92 (1802), стр. 12–48, читать 12 ноября 1801 г.
↑ Дарригол, 2012, стр. 101–102; Ньютон , 1730, Книга III , Часть I.
^ Дарригол, 2012, стр. 177–179.
↑ Янг, 1855, стр. 188.
↑ Янг, 1855, стр. 179–181.
^ Дарригол, 2012, стр. 187.
^ Гюйгенс, 1690, tr. Томпсон, стр. 92–94. Для простоты приведенный выше текст описывает частный случай; описание Гюйгенса имеет большую общность.
↑ Ньютон, 1730, стр. 358–361.
↑ Ньютон, 1730, стр. 373–374.
↑ Ньютон, 1730, стр. 363.
↑ Ньютон, 1730, стр. 356.
^ ab Buchwald, Jed Z. (1 декабря 1980 г.). "Экспериментальные исследования двойного преломления от Гюйгенса до Малуса". Архив для History of Exact Sciences . 21 (4): 311–373. doi :10.1007/BF00595375. ISSN 1432-0657.Как отмечает автор, альтернативные правила для необыкновенной рефракции были предложены Ла Гиром в 1710 году и Гаюи в 1788 году (см. стр. 332–334, 335–337 соответственно).
^ Франкель (1974) и Янг (1855, стр. 225–228) развенчивают утверждение Лапласа об установлении существования такой силы. Френель (1827, tr. Hobson, стр. 239–241) более подробно рассматривает механические трудности этого утверждения. По общему признанию, конкретное утверждение, которое он приписывает Лапласу, не встречается в соответствующем отрывке из сочинений Лапласа (приложенном к мемуарам Френеля переводчиком), который похож на отрывок, ранее разгромленный Янгом; однако эквивалентное утверждение встречается в работах Малуса ( Mémoires de Physique et de Chimie, de la Société d'Arcueil , т. 2, 1809, стр. 266, цитируется в переводе Силлимана, 1967, стр. 131).
↑ Young, 1855, стр. 228–232; ср. Whewell, 1857, стр. 329.
^ Дарригол, 2012, стр. 191–192; Силлиман, 1967, стр. 125–127.
↑ Брюстер, Дэвид (31 декабря 1815 г.). «IX. О законах, регулирующих поляризацию света при отражении от прозрачных тел». Philosophical Transactions of the Royal Society of London . 105 : 125–159. doi :10.1098/rstl.1815.0010. ISSN 0261-0523. JSTOR 107362 .
^ Дарригол, 2012, с. 192; Силлиман, 1967, с. 128.
↑ Янг, 1855, стр. 249–250.
↑ Янг, 1855, стр. 233.
^ Левитт, 2009, с. 37; Дарригол, 2012, стр. 193–194, 290.
^ Darrigol, 2012, стр. 194–195 (обычная интенсивность); Frankel, 1976, стр. 148 (обе интенсивности).
^ Бухвальд, 1989, стр. 79–88; Левитт, 2009, стр. 33–54.
^ ab Buchwald, JZ (май 1989). «Битва между Араго и Биотом за Френеля». Journal of Optics . 20 (3): 109–117. Bibcode : 1989JOpt...20..109B. doi : 10.1088/0150-536X/20/3/002. ISSN 0150-536X.
^ Франкель, 1976, стр. 149–150; Бухвальд, 1989, стр. 99–103; Дарригол, 2012, стр. 195–196.
^ Франкель, 1976, стр. 151–152; Дарригол, 2012, с. 196.
↑ Янг, 1855, стр. 269–272.
^ ab Frankel, 1976, стр. 176; ср. Silliman, 1967, стр. 142–143.
^ Франкель, 1976, стр. 155.
^ Бухвальд, 1989, стр. 116–117; Силлиман, 1967, стр. 40–45; Френель, 1866–70, т. 2, стр. 831; Левитт, 2009, стр. 49.
↑ Бутри, 1948, стр. 594–595.
↑ Предположительно GW Jordan, The Observations of Newton Concerning the Inflections of Light; Accompaned by Other Observations Disferring from His; and Appearing to Lead to a Change of His Theory of Light and Colours (также цитируется как New Observations concerning the Inflections of Light ), London: T. Cadell Jr. & W. Davies, 1799; рассмотрено в TG Smollett (ed.), The Critical Review, Or, Annals of Literature (London), vol. 34, pp. 436–443 (апрель 1802 г.).
↑ Френель, 1866–70, т. 1, стр. 6n; Кипнис, 1991, стр. 167; выделение добавлено.
^ Френель, 1866–70, т. 1, стр. 6–7.
↑ Fresnel, 1866–70, т. 1, стр. xxxi (микрометр, слесарь [ serrurier ], опоры), 6n (слесарь); Buchwald, 1989, стр. 122 (медовая капля), 125–126 (микрометр, со схемой); Boutry 1948, стр. 595 и Levitt, 2013, стр. 40 (слесарь, медовая капля, микрометр); Darrigol 2012, стр. 198–199 (слесарь, медовая капля).
^ Бухвальд, 1989, стр. 122, 126; Силлиман, 1967, стр. 147–149.
^ Левитт, 2013, стр. 39, ‍ 239 .
^ Кипнис, 1991, стр. 167; Френель, 1866–70, т. 1, стр. 5–6.
↑ Darrigol, 2012, стр. 198. Силлиман (1967, стр. 146) идентифицирует брата как Фульженса, тогда находившегося в Париже; ср. Fresnel, 1866–70, т. 1, стр. 7n.
^ Дарригол, 2012, стр. 199.
^ Бухвальд, 1989, стр. 119, 131–132; Дарригол, 2012, стр. 199–201; Кипнис, 1991, стр. 175–176.
^ Дарригол, 2012, стр. 201.
↑ Френель, 1866–70, т. 1, стр. 48–49; Кипнис, 1991, стр. 176–178.
↑ Франкель, 1976, стр. 158; Френель, 1866–70, т. 1, стр. 9n.
↑ Френель, 1866–70, т. 1, стр. 38; курсив добавлен.
^ Бухвальд, 1989, стр. 137–139.
↑ Young, 1807, т. 1, стр. 787 и рис. 442, ‍ 445 ; Young, 1855, стр. 180–181, 184.
↑ Янг Араго (на английском языке), 12 января 1817 г., в Young, 1855, стр. 380–384, на стр. 381; цитируется в Silliman, 1967, стр. 171.
^ Ньютон, 1730, стр. 321, рис. 1, где прямые лучи DG, EH, FI вносят вклад в изогнутую траекторию полосы, так что одна и та же полоса создается разными лучами на разных расстояниях от препятствия (ср. Дарригол, 2012, стр. 101, рис. 3.11 – где в подписи «1904» должно быть «1704», а « CFG » должно быть « CFI »).
^ Кипнис, 1991, стр. 204–205.
^ Силлиман, 1967, стр. 163–164; Франкель, 1976, стр. 158; Бутри, 1948, стр. 597; Левитт, 2013, стр. 41–43, 239.
^ Силлиман, 1967, стр. 165–166; Бухвальд, 1989, стр. 137; Кипнис, 1991, стр. 178, 207, 213.
↑ Френель, 1816.
^ Дарригол, 2012, с. 201; Франкель, 1976, с. 159.
^ Кипнис, 1991, стр. 166n, ‍ 214n .
^ Кипнис, 1991, стр. 212–214; Франкель, 1976, стр. 159–160, 173.
↑ См. Young, 1807, т. 1, стр. 777 и рис. 267.
↑ Darrigol, 2012, стр. 201; письмо напечатано в Young, 1855, стр. 376–378, а его заключение переведено Силлиманом (1967, стр. 170).
↑ Френель, 1866–70, т. 1, стр. 129–170.
^ Силлиман, 1967, стр. 177–179; Дарригол, 2012, стр. 201–203.
^ Бухвальд, 1989, стр. 134–135, 144–145; Силлиман, 1967, стр. 176–177.
^ Силлиман, 1967, стр. 173–175; Бухвальд, 1989, стр. 137–138; Дарригол, 2012, стр. 201–2; Бутри, 1948, с. 597; Френель, 1866–70, т. 1, с. 1, стр. 123–128 (заявление Араго).
^ Левитт, 2013, стр. 43; Бутри, 1948, стр. 599.
↑ Араго, 1857, стр. 404–405.
^ Левитт, 2013, стр. 28, 237.
^ Kipnis, 1991, стр. 218; Buchwald, 2013, стр. 453; Levitt, 2013, стр. 44. Frankel (1976, стр. 160–161) и Grattan-Guinness (1990, стр. 867) отмечают, что тема была впервые предложена 10 февраля 1817 года. Только Darrigol (2012, стр. 203) говорит, что конкурс был «открыт» 17 марта 1818 года . Премии предлагались в нечетные годы по физике и в четные годы по математике (Frankel, 1974, стр. 224n).
↑ Бухвальд, 1989, стр. 169–171; Франкель, 1976, стр. 161; Силлиман, 1967, стр. 183–184; Френель, 1866–70, т. 1, стр. xxxvi–xxxvii.
↑ Френель, 1866–70, т. 1, стр. xxxv; Левитт, 2013, стр. 44.
^ Силлиман, 2008, стр. 166; Франкель, 1976, стр. 159.
↑ Fresnel, 1866–70, т. 1, стр. xxxv, xcvi; Boutry, 1948, стр. 599, ‍ 601. Силлиман (1967, стр. 180) называет начальной датой 1 мая 1818 года.
^ Френель, 1866–70, том. 1, с. xcvi; Араго, 1857, с. 466.
^ abcd G. Ripley и CA Dana (ред.), "Fresnel, Augustin Jean", American Cyclopædia , 1879, т. 7, стр. 486–489. Вопреки этой записи (стр. 486), кальцит и кварц были не единственными кристаллами с двойным преломлением, известными до Френеля; см. (например) Young, 1855, стр. 250 (написано в 1810 г.) и стр. 262, ‍ 266 , ‍ 277 (написано в 1814 г.), и Lloyd, 1834, стр. 376–377.
^ abcd А. Френель, «Дополнение к мемуарам о модификациях поляризованного света, которые отражение производит»), подписано 15 января 1818 г., передано для свидетеля 19 января. 1818 г.; напечатано Френелем, 1866–70, вып. 1, стр. 487–508.
↑ Напечатано в издании Fresnel, 1866–70, т. 1, стр. 171–181.
↑ См. Френель, 1866–70, т. 1, стр. 174–175; Бухвальд, 1989, стр. 157–158.
^ Бухвальд, 1989, стр. 167; 2013, стр. 454.
↑ Френель, 1818б.
^ См. Френеля, 1818b, в Mémoires de l'Académie Royale des Sciences… , vol. В , с. 339n, и у Френеля, 1866–70, вып. 1, с. 247, примечание 1.
↑ Френель, 1866–70, т. 1, стр. 247; Крю, 1900, стр. 79; Левитт, 2013, стр. 46.
↑ Crew, 1900, стр. 101–108 (векторное представление), 109 (отсутствие ретроградного излучения), 110–111 (направленность и расстояние), 118–122 (вывод интегралов), 124–125 (максимумы и минимумы), 129–131 (геометрическая тень).
^ Дарригол, 2012, стр. 204–205.
↑ Crew, 1900, стр. 127–128 (длина волны), 129–131 (полуплоскость), 132–135 (экстремумы, щель); Fresnel, 1866–70, т. 1, стр. 350–355 (узкая полоска).
^ Бухвальд, 1989, стр. 179–182.
↑ Экипаж, 1900, стр. 144.
↑ Френель, 1866–70, т. 1, стр. xlii; Уорралл, 1989, стр. 136; Бухвальд, 1989, стр. 171, 183; Левитт, 2013, стр. 45–46.
^ Левитт, 2013, стр. 46.
↑ Frankel, 1976, стр. 162. Однако Kipnis (1991, стр. 222–224) приводит доказательства того, что неудачливым участником был Оноре Фложерг (1755–1830?) и что суть его записи содержится в «дополнении», опубликованном в Journal de Physique , т. 89 (сентябрь 1819 г.), стр. 161–186.
↑ Френель, 1866–70, т. 1, стр. 236–237.
^ Уорралл, 1989, стр. 139–140.
^ См. Уорралл, 1989, стр. 141.
^ Б. Уотсон, Свет: Лучезарная история от сотворения мира до квантовой эпохи , Нью-Йорк: Bloomsbury, 2016.
^ Дарригол, 2012, с. 205; Френель, 1866–70, т. 1, с. 1, с. XLII.
↑ Френель, 1866–70, т. 1, стр. xlii; Уорралл, 1989, стр. 141.
↑ Френель, 1866–70, т. 1, стр. 229–246.
↑ Френель, 1866–70, т. 1, стр. 229, примечание 1; Граттан-Гиннесс, 1990, стр. 867; Левитт, 2013, стр. 47.
↑ Френель, 1866–70, т. 1, стр. 237; Уорралл, 1989, стр. 140.
^ ab Académie des Sciences, Proces-verbaux des séances de l'Académie tenues depuis la Fondation de l'Institut jusqu'au mois d'août 1835 , vol. VI (за 1816–1819 гг.), Андай, Нижние Пиренеи: Imprimerie de l'Observatoire d'Abbadia, 1915.
↑ Френель, 1866–70, т. 1, стр. 230n.
^ Уорралл, 1989, стр. 135–138; Кипнис, 1991, стр. 220.
^ Worrall, 1989, стр. 143–145. Печатная версия отчета также ссылается на примечание (E), но это примечание касается дальнейших исследований, которые имели место после того, как была определена премия (Worrall, 1989, стр. 145–146; Fresnel, 1866–70, т. 1, стр. 236, 245–246). Согласно Кипнису (1991, стр. 221–222), реальное значение пятна Пуассона и его дополнения (в центре диска света, отбрасываемого круглой апертурой ) заключалось в том, что они касались интенсивностей полос, тогда как измерения Френеля касались только положения полос; но, как также отмечает Кипнис, этот вопрос был рассмотрен только после того, как была определена премия.
^ Относительно их более поздних взглядов см. §‍Reception.
^ Бухвальд, 1989, стр. 183–184; Дарригол, 2012, с. 205.
^ Кипнис, 1991, стр. 219–220, 224, 232–233; Граттан-Гиннесс, 1990, стр. 870.
^ Бухвальд, 1989, стр. 186–198; Дарригол, 2012, стр. 205–206; Кипнис, 1991, стр. 220.
^ Бухвальд, 1989, стр. 50–51, 63–5, 103–104; 2013, стр. 448–449.
^ Бухвальд, 1989, стр. 203, ‍ 205 ; Дарригол, 2012, с. 206; Силлиман, 1967, стр. 203–205.
↑ Араго и Френель, 1819.
^ Дарригол, 2012, с. 207; Франкель, 1976, стр. 163–164, 182.
^ Дарригол, 2012, стр. 206.
^ Франкель, 1976, стр. 164.
^ Бухвальд, 1989, стр. 386.
^ Бухвальд, 1989, стр. 216, ‍ 384 .
↑ Бухвальд, 1989, стр. 333–336; Дарригол, 2012, стр. 207–208. (Дарригол указывает дату 1817 год, но номера страниц в его сноске 95 соответствуют его ссылке «1818b», а не «1817».)
↑ Френель, 1866–70, т. 1, стр. 533–537. О происхождении заметки см. стр. 523. В приведенном выше тексте φ — это сокращение от френелевского 2 π ( e − o ) , где e и o — это числа циклов, затраченных необыкновенной и обыкновенной волнами на прохождение через пластину.
^ Бухвальд, 1989, стр. 97; Франкель, 1976, стр. 148.
↑ Френель, 1821б.
↑ Френель, 1821б, §3.
↑ Френель, 1821b, §1 и сноски.
^ Бухвальд, 1989, стр. 237–251; Франкель, 1976, стр. 165–168; Дарригол, 2012, стр. 208–209.
↑ Френель, 1821а, §10.
↑ Френель, 1866–70, т. 1, стр. 394n; Френель, 1821a, §10; Силлиман, 1967, стр. 209–210; Бухвальд, 1989, стр. 205–206, 208, 212, 218–219.
↑ Янг, 1855, стр. 383.
↑ ab T. Young, «Chromatics» (написано в сентябре–октябре 1817 г.), Приложение к четвертому, пятому и шестому изданиям Encyclopaedia Britannica , т. 3 (выпущено в феврале 1818 г.), перепечатано в Young, 1855 г., стр. 279–342.
↑ Бухвальд, 1989, стр. 225–226; Френель, 1866–70, т. 1, стр. 526–527, 529.
^ Бухвальд, 1989, стр. 226.
^ Френель, 1821а.
^ Бухвальд, 1989, стр. 227; Френель, 1821a, §1.
^ Бухвальд, 1989, стр. 212; Френель, 1821a, §10.
↑ Френель, 1821a, §10; выделение добавлено.
↑ Френель, 1821a, §13; ср. Бухвальд, 1989, стр. 228.
^ См. Бухвальд, 1989, стр. 230.
^ "Эта гипотеза г-на Френеля по крайней мере очень остроумна и может привести нас к некоторым удовлетворительным вычислениям: но она сопровождается одним обстоятельством, которое совершенно ужасает по своим последствиям. Вещества, на которых г-н Савар проводил свои эксперименты, были только твердыми телами ; и только твердым телам когда-либо приписывалось такое боковое сопротивление: так что если мы примем различия, изложенные самим возродителем волновой системы в его Лекциях , то можно будет сделать вывод, что светоносный эфир, пронизывающий все пространство и проникающий почти во все вещества, не только высокоэластичен, но и абсолютно тверд!!!" — Томас Янг (написано в январе 1823 г.), раздел  XIII в "Преломлении, двойном и поляризованном свете", Дополнение к Четвертому, Пятому и Шестому изданиям Британской энциклопедии , т. 6 (1824 г.), на стр. 862, перепечатано в Young, 1855, на стр. 415 (курсив и восклицательные знаки в оригинале). «Лекции», которые Янг цитирует далее, принадлежат ему самому (Young, 1807, т. 1, стр. 627).
^ Бухвальд, 1989, стр. 388–390; Френель, 1821a, §18.
^ Бухвальд, 1989, стр. 390–391; Френель, 1821a, §§ 20–22.
^ abcd A. Fresnel, "Mémoire sur la loi des modifications que la réflexion imprime à la lumière polarisée" ("Mémoire sur la loi des modifications que la réflexion imprime à la lumière polarisée"), прочитано 7 января 1823 г.; перепечатано в Fresnel, 1866–70, т. 1, стр. 767–799 (полный текст, опубликован в 1831 г.), стр. 753–762 (выдержка, опубликована в 1823 г.). См. особенно стр. 773 (закон синусов), 757 (закон тангенсов), 760–761 и 792–796 (углы полного внутреннего отражения для заданных разностей фаз).
^ Бухвальд, 1989, стр. 391–393; Уиттекер, 1910, стр. 133–135.
^ Уиттакер, 1910, с. 134; Дарригол, 2012, с. 213; Френель, 1866–70, т. 1, с. 1, стр. 773, ‍ 757 .
^ Бухвальд, 1989, стр. 393–394; Уиттекер, 1910, стр. 135–136; Френель, 1866–70, т. 1, стр. 760–761, 792–796.
^ Уиттекер, 1910, стр. 177–179; Бухвальд, 2013, стр. 467.
^ abc А. Френель, «Mémoire sur la double refraction que les rayons lumineux éprouvent en traversant les aiguilles de cristal de roche suivant les Directions parallèles à l'axe» («Мемуары о двойном преломлении, которому подвергаются световые лучи при прохождении игл горный хрусталь [кварц] в направлениях, параллельных оси»), прочитано 9 декабря 1822 г.; напечатано Френелем, 1866–70, вып. 1, стр. 731–751 (полный текст), стр. 719–29 (отрывок, впервые опубликованный в Bulletin de la Société philomatique за 1822 г., стр. 191–198).
^ Бухвальд, 1989, стр. 230–232, 442.
^ См. Бухвальд, 1989, стр. 232.
↑ Статья о Брюстере, «О новом виде подвижной поляризации», [Quarterly] Journal of Science and the Arts , т. 2, № 3, 1817, стр. 213.
↑ Ллойд, 1834, стр. 368.
^ Дарригол, 2012, стр. 207.
^ A. Fresnel, "Mémoire sur les modifications que la réflexion imprime à la lumière polarisée" ("Воспоминания об изменениях, которые отражение производит на поляризованный свет"), подписано и представлено 10 ноября 1817 г., прочитано 24 ноября 1817 г.; напечатано в Fresnel, 1866–70, т. 1, стр. 441–485, включая стр. 452 (повторное открытие деполяризации полным внутренним отражением), 455 (два отражения, "связанные призмы", "параллелепипед в стекле"), 467–8 (разность фаз на отражение); см. также стр. 487, примечание 1 (дата прочтения). Кипнис (1991, стр. 217n) подтверждает прочтение и добавляет, что статья была опубликована в 1821 г.
^ Бухвальд, 1989, стр. 223, ‍ 336 ; на последней странице «призма» означает ромб Френеля или эквивалент. Сноска в мемуарах 1817 года (Френель, 1866–70, т. 1, стр. 460, примечание 2) описывала эмулятор более кратко и не в самодостаточной манере.
↑ Френель, 1818а, особенно стр. 47–49.
^ Дженкинс и Уайт, 1976, стр. 576–579 (§ 27.9, особенно рис. 27M).
^ Иллюстрации см. в JM Derochette, «Conoscopy of biaxial minerals (1)», www.jm-derochette.be , 2004; архивировано 1 мая 2017 г.
^ Бухвальд, 1989, стр. 254–255, 402.
^ См. Бухвальд, 1989, стр. 269.
^ Граттан-Гиннесс, 1990, стр. 885.
^ Бухвальд, 1989, стр. 269, ‍ 418 .
^ Ж.-Б. Био, «Mémoire sur les lois générales de la double refraction et de la поляризации, dans les corps régulièrement cristallisés» (прочитано 29 марта 1819 г.), Mémoires de l'Académie Royale des Sciences… , vol. III (за 1818 г. [ так в оригинале ], напечатано в 1820 г.), стр. 177–384; «Extrait d'un Mémoire sur les lois de la double refraction et de la Polarization dans les corps régulièrement cristallisés», Bulletin des Sciences par la Société Philomathique de Paris , 1820, стр. 12–16, включая стр. 13–14 (sine закон), 15–16 (двугранный закон).
↑ См. Френель, 1822a, пер. Янг, в «Quarterly Journal of Science, Literature, and Art» , июль–декабрь 1828 г., стр. 178–179.
^ Бухвальд, 1989, стр. 260.
↑ Напечатано в издании Fresnel, 1866–70, т. 2, стр. 261–308.
^ Silliman, 1967, стр. 243–246 (первый эксперимент); Buchwald, 1989, стр. 261–267 (оба эксперимента). Первый эксперимент был кратко описан ранее в Fresnel, 1821c.
↑ Бухвальд (1989, стр. 267–272) и Граттан-Гиннесс (1990, стр. 893–894) называют его «эллипсоидом упругости».
^ Бухвальд, 1989, стр. 267–272; Граттан-Гиннесс, 1990, стр. 885–887.
^ Бухвальд, 1989, стр. 274–279.
^ Бухвальд, 1989, стр. 279–280.
↑ Буквально «поверхность волны» — как в переводе Гобсона Френеля 1827 года.
^ Френель, 1866–70, т. 2, стр. 340, 361–363; Бухвальд, 1989, стр. 281–283. Вывод «волновой поверхности» из ее касательных плоскостей был в конечном итоге осуществлен Ампером в 1828 году (Ллойд, 1834, стр. 386–387; Дарриголь, 2012, стр. 218; Бухвальд, 1989, стр. 281, ‍ 457 ).
↑ Френель, 1866–70, т. 2, стр. 369–442.
^ Бухвальд, 1989, стр. 283–285; Дарригол, 2012, стр. 217–218; Френель, 1866–70, т. 1, с. 2, стр. 386–388.
^ В. Н. Гриффин, Теория двойного лучепреломления, Кембридж: Т. Стивенсон, 1842.
↑ Граттан-Гиннесс, 1990, стр. 891–892; Френель, 1866–70, т. 2, стр. 371–379.
↑ Бухвальд, 1989, стр. 285–286; Френель, 1866–70, т. 2, стр. 396.
^ Ланни, Джеймс Г.; Вайр, Денис (1 мая 2006 г.). «Внутри и снаружи конической рефракции». Europhysics News . 37 (3): 26–29. Bibcode : 2006ENews..37c..26L. doi : 10.1051/epn:2006305 . ISSN 0531-7479.
^ Grattan-Guinness, 1990, стр. 896–897. Silliman, 1967, стр. 262–263; 2008, стр. 170
^ Бухвальд, 1989, стр. 286–287, 447.
^ Френель, 1827.
^ Френель, 1866–70, т. 2, стр. 800n. Хотя в оригинальной публикации (Френель, 1827) в некоторых нижних колонтитулах указан год «1824», известно, что Френель, замедленный болезнью, не закончил мемуары до 1826 года (Бухвальд, 1989, стр. 289, ‍ 447 , цитируя Френеля, 1866–70, т. 2, стр. 776n).
↑ Френель, 1827, труд Хобсона, стр. 266–273.
↑ Френель, 1827, труд Хобсона, стр. 281–285.
↑ Френель, 1827, труды Хобсона, стр. 320–322; Бухвальд, 1989, стр. 447.
^ Grattan-Guinness, 1990, стр. 1003–1009, 1034–1040, 1043; Whittaker, 1910, стр. 143–145; Darrigol, 2012, стр. 228. Grattan-Guinness приводит доказательства против любой более ранней датировки теорий Коши.
^ Уиттекер, 1910, глава V ; Дарригол, 2012, глава 6; Бухвальд, 2013, стр. 460–464.
↑ Френель, 1827, пер. Хобсон, стр. 273–281; Силлиман, 1967, стр. 268n; Бухвальд, 1989, стр. 288.
↑ Брюстер, Дэвид (31 декабря 1815 г.). «V. О влиянии простого давления на создание того вида кристаллизации, который образует два противоположно поляризованных изображения и демонстрирует дополнительные цвета поляризованным светом». Philosophical Transactions of the Royal Society of London . 105 : 60–64. doi :10.1098/rstl.1815.0006. ISSN 0261-0523. JSTOR 107358 .
↑ Брюстер, Дэвид (31 декабря 1816 г.). «X. О передаче структуры двоякопреломляющих кристаллов стеклу, хлористому натру, плавиковому шпату и другим веществам посредством механического сжатия и расширения». Philosophical Transactions of the Royal Society of London . 106 : 156–178. doi :10.1098/rstl.1816.0011. ISSN 0261-0523. JSTOR 107522 .
↑ A. Fresnel, «Note sur la double réfraction du verre comprimé» («Заметка о двойном преломлении сжатого стекла»), прочитано 16 сентября 1822 г., опубликовано в 1822 г.; перепечатано в Fresnel, 1866–70, т. 1, стр. 713–718, на стр. 715–717.
↑ Уэвелл, 1857, стр. 355–356.
↑ Френель, 1866–70, т. 1, стр. 737–739 (§4). См. Whewell, 1857, стр. 356–358; Jenkins & White, 1976, стр. 589–590.
^ Френель, 1822а.
^ Граттан-Гиннесс, 1990, стр. 884.
^ См. Франкель, 1976, стр. 169.
↑ Френель, 1866–70, т. 2, стр. 261n, ‍ 369n .
↑ Напечатано в издании Fresnel, 1866–70, т. 2, стр. 459–464.
^ Бухвальд, 1989, стр. 288.
^ Френель, 1866–70, том. 1, стр. lxxxvi–lxxxvii; Граттан-Гиннесс, 1990, с. 896.
^ Граттан-Гиннесс, 1990, стр. 898.
^ Бухвальд, 1989, стр. 289–390.
↑ Frankel, 1976, стр. 170–171; ср. Fresnel, 1827, пер. Hobson, стр. 243–244, 262.
^ Силлиман, 1967, стр. 284–285, цитируя Френеля, 1866–70, т. 1, стр. lxxxix, примечание 2. Франкель (1976, стр. 173) соглашается. Уорралл (1989, стр. 140) настроен скептически.
^ Франкель, 1976, стр. 173–174.
↑ Дж. Ф. У. Гершель, «Свет», Encyclopaedia Metropolitana , т. 4 (Лондон, 1845; переиздано в 1849), стр. 341–586; перепечатано (с оригинальными номерами страниц и приложенными иллюстрациями) в JFW Herschel, Treatises on Physical Astronomy, Light and Sound, внесённом в Encyclopaedia Metropolitana , Лондон и Глазго: R. Griffin & Co. (без даты).
^ Бухвальд, 1989, стр. 291–296; Дарригол, 2012, стр. 220–221, 303.
^ Френель, 1822a; Кипнис, 1991, стр. 227–228.
^ Бухвальд, 1989, стр. 296.
↑ Дж. Б. Эйри, «О дифракции объектива с круглым отверстием», Труды Кембриджского философского общества , т. V , часть III (1835), стр. 283–291 (прочитано 24 ноября 1834 г.).
^ Дарригол, 2012, стр. 222–223, 248.
^ Кипнис, 1991, стр. 225, ‍ 227 ; Дарригол, 2012, стр. 223, ‍ 245 .
↑ Whewell, 1857, стр. 340–341; цитируемые абзацы относятся к 1-му изданию (1837).
↑ Уэвелл, 1857, стр. 482–483; Уиттакер, 1910, стр. 136; Дарригол, 2012, стр. 223.
^ T. Tag, «Использование линз до Френеля», US Lighthouse Society, доступ 12 августа 2017 г.; архив 20 мая 2017 г.
^ Левитт, 2013, стр. 57.
^ ab Levitt, 2013, стр. 59.
^ Н. де Кондорсе, Éloge de M. le Comte de Buffon, Париж: Chez Buisson, 1790, стр. 11–12.
^ abcde T. Tag, «Линза Френеля», US Lighthouse Society, доступ 12 августа 2017 г.; архив 22 июля 2017 г.
^ ab Levitt, 2013, стр. 71.
↑ D. Appleton & Co., «Морские огни», Словарь машин, механики, машиностроения и машиностроения , 1861, т. 2, стр. 606–618.
^ T. Tag, «Хронология событий маяков», US Lighthouse Society, доступ 22 августа 2017 г.; архив 8 апреля 2017 г.
↑ Чисхолм, Хью , ред. (1911), «Брюстер, сэр Дэвид» , Encyclopaedia Britannica , т. 4 (11-е изд.), Cambridge University Press, стр. 513–514..
↑ Левитт, 2013, стр. 51, ‍ 53 ; Френель, 1866–70, т. 1, стр. xcvii, и т. 3, стр. xxiv.
^ Левитт, 2013, стр. 49–50.
↑ Френель, 1866–70, т. 3, стр. 5–14; о дате см. стр. 6n.
^ Левитт, 2013, стр. 56, ‍ 58 .
^ Левитт, 2013, стр. 59–66. О размерах см. Элтон, 2009, стр. 193–194; Френель, 1866–70, т. 3, стр. xxxiv; Френель, 1822b, tr. Tag, стр. 7.
^ Д. Гомбер, фотография Optique de Cordouan из коллекции Musée des Phares et Balises, Уэссан , Франция, 23 марта 2017 г.
↑ Френель, 1822b, tr. Tag, стр. 13, ‍ 25 .
^ Элтон, 2009, стр. 195; Левитт, 2013, стр. 72–76.
^ ab Levitt, 2013, стр. 97.
^ Левитт, 2013, стр. 82.
^ Элтон, 2009, стр. 190.
↑ Grattan-Guinness, 1990, стр. 914–915, цитируя Young, 1855, стр. 399; Arago, 1857, стр. 467, 470; Boutry, 1948, стр. 601–602.
^ См. Элтон, 2009, стр. 198, рисунок 12.
^ Левитт, 2013, стр. 84.
^ Элтон, 2009, стр. 197–198.
^ Элтон, 2009, стр. 198–199.
^ Левитт, 2013, стр. 82–84.
^ Элтон, 2009, стр. 200.
^ Левитт, 2013, стр. 79–80.
^ Национальный морской музей, «Appareil catadioptrique, Appareil du canal Saint-Martin», по состоянию на 26 августа 2017 г.; в архиве 26 августа 2017 г.
^ Элтон, 2009, стр. 199, ‍ 200 , ‍ 202 ; Левитт, 2013, стр. 104–105.
^ Левитт, 2013, стр. 108–110, 113–116, 122–123.
^ T. Tag, «Линзы Френеля американского производства», US Lighthouse Society, дата обращения 1 марта 2021 г.; архивировано 21 февраля 2021 г.
↑ А. Финстад, «Новые разработки в области аудиовизуальных материалов», Высшее образование , т. 8, № 15 (1 апреля 1952 г.), стр. 176–178, на стр. 176.
^ ab Kipnis, 1991, стр. 217.
^ Франкель, 1976, стр. 172.
↑ Grattan-Guinness, 1990, стр. 861, 913–914; Arago, 1857, стр. 408. Силлиман (1967, стр. 262n) называет даты соответствующих выборов 27 января и 12 мая 1823 года.
^ Левитт, 2013, стр. 77.
↑ Янг, 1855, стр. 402–403.
↑ Королевское общество, Список членов Королевского общества 1660–2007 , A–J, июль 2007 г., стр. 130.
↑ GE Rines (ред.), «Френель, Огюстен Жан», Encyclopedia Americana , 1918–20, т. 12 (1919), стр. 93. (Эта запись неточно описывает Френеля как «первооткрывателя» поляризации света и как «члена» Королевского общества, тогда как на самом деле он объяснил поляризацию и был «иностранным членом» Общества; см. текст.)
↑ Королевское общество, «Медаль Рамфорда» (со ссылкой на полный список прошлых победителей), дата обращения 2 сентября 2017 г.
^ Дж. Жамин, Disours prononcé au nom de l'Académie des Sciences à l'inuguration du Monument de Fresnel, Бройль, 14 сентября 1884 г.; по состоянию на 6 сентября 2017 г.
^ Левитт, 2013, стр. 233.
^ IAU WGPSN , «Promontorium Fresnel» и «Rimae Fresnel», Gazetteer of Planetary Nomenclature , дата обращения 19 декабря 2017 г.
^ Левитт, 2013, стр. 75–76; Силлиман, 1967, стр. 276–277.
↑ Boutry, 1948, стр. 601–602; Silliman, 1967, стр. 278; Fresnel, 1866–70, т. 2, стр. 667–672.
↑ Френель, 1866–70, т. 2, стр. 647–660.
↑ Бутри, 1948, стр. 603.
^ Левитт, 2013, стр. 98; Силлиман, 1967, стр. 279; Араго, 1857, стр. 470; Бутри, 1948, стр. 602–603 .
↑ Френель, 1866–70, т. 2, стр. 800n.
^ Бухвальд, 1989, стр. 289.
↑ Френель, 1818а.
^ Кипнис, 1991, стр. 207n, ‍ 217n ; Бухвальд, 1989, стр. 461, ссылка 1818d; Френель, 1866–70, т. 1, стр. 655n.
↑ В Тейлоре, 1852, стр. 44–65.
^ Бухвальд, 1989, стр. 222, 238, 461–462.
^ Граттан-Гиннесс, 1990, стр. 861.
↑ Уиттекер, 1910, стр. 125n.
↑ Boutry, 1948, стр. 603–604; Fresnel, 1866–70, т. 1, стр. i–vii.
^ Силлиман, 2008, стр. 171.
^ ab AKT Assis и JPMC Chaib, Ampère's Electrodynamics («Анализ значения и эволюции силы Ампера между элементами тока, вместе с полным переводом его шедевра: Теория электродинамических явлений, однозначно выведенная из опыта »), Монреаль: Apeiron, 2015.
^ Ж. Жубер (редактор), Collection de Mémoires relatifs à la Physique , vol. 2 (часть 1 «Mémoires sur l'électrodynamique» ), Париж: Готье-Виллар, 1885, стр. 140 (признательность Ампера), 141–147 (примечания Френеля).
^ Бухвальд, 1989, стр. 116.
↑ Френель, 1866–70, т. 2, стр. 768n, 802.
↑ Френель, 1866–70, т. 2, стр. 803n. Граттан-Гиннесс (1990, стр. 884n) указывает годом создания 1825, но это не соответствует первоисточникам.
^ См. Дарригол, 2012, стр. 258–260.
↑ Френель, 1818c.
^ Дарригол, 2012, с. 212; Френель, 1821а, §§ 14, 18.
^ Darrigol, 2012, стр. 246; Buchwald, 1989, стр. 307–308; Fresnel, 1822a, tr. Young, в Quarterly Journal of Science, Literature, and Art , янв.–июнь 1828 г., на стр. 213–215. Whittaker, 1910, стр. 132; Fresnel, 1866–70, т. 2, стр. 438.
↑ Френель, 1827, пер. Хобсон, стр. 277n, ‍ 331n ; Ллойд, 1834, стр. 316.
^ Френель, 1866–70, том. 1, с. xcvi.
^ Уиттекер, 1910, стр. 182–183; Уэвелл, 1857, стр. 365–367; Дарригол, 2012, стр. 246–249.
^ Дарригол, 2012, стр. 252.
↑ Ллойд, 1834, стр. 387–388.
^ ab MacCullagh, James (1830). «О двойном преломлении света в кристаллизованной среде согласно принципам Френеля». Труды Королевской Ирландской Академии . 16 : 65–78. ISSN 0790-8113. JSTOR 30079025 .
↑ WR Hamilton, «Третье дополнение к эссе о теории систем лучей», Transactions of the Royal Irish Academy , т. 17, стр. v–x, 1–144, прочитано 23 января и 22 октября 1832 г.; jstor.org/stable/30078785 (введение автора датировано июнем 1833 г.; том начат в 1831 (?), закончен в 1837 г.).
↑ Phare de Cordouan, «Системы освещения маяка Кордуан», дата обращения 26 августа 2017 г.; архивировано 22 сентября 2016 г.
^ Левитт, 2013, стр. 19.
^ Левитт, 2013, стр. 8.
↑ Фонд Джеймса Клерка Максвелла, «Кто был Джеймс Клерк Максвелл?», дата обращения 6 августа 2017 г.; архивировано 30 июня 2017 г.
↑ Ллойд, 1834, стр. 382.
↑ Уэвелл, 1857, стр. 370–371.
↑ Вступительное предложение в работе Э. М. Антониади «Столетие Огюстена Френеля», L'Astronomie (Париж), т. 41, стр. 241–246 (июнь 1927 г.), переведено как «Столетие Огюстена Френеля» в Ежегодном отчете Совета регентов Смитсоновского института , Вашингтон, 1927 г., стр. 217–220.

Общие и цитируемые ссылки

DFJ Arago (перевод B. Powell), 1857, «Френель» (элегия, прочитанная на публичном собрании Академии наук 26 июля 1830 г.), в DFJ Arago (перевод WH Smyth, B. Powell и R. Grant), Biographies of Distinguished Scientific Men (однотомное издание), Лондон: Longman, Brown, Green, Longmans, & Roberts, 1857, стр. 399–471. (О личности переводчика см. стр. 425n, ‍ 452n .) Исправление : В примечании переводчика на стр. 413 плоскость, касательная к внешней сфере в точке t, должна пересекать преломляющую поверхность (предполагаемую плоской); затем через это пересечение следует провести касательные плоскости к внутренней сфере и сфероиду (ср. Мах, 1926, стр. 263).
DFJ Араго и А. Френель, 1819, «Mémoire sur l'action que les rayons de lumière Polarisée exercent les uns sur les autres», Annales de Chimie et de Physique , Ser. 2, том. 10, стр. 288–305, март 1819 г.; перепечатано во Френеле, 1866–70, т. 1, стр. 509–522; переведено как «О действии лучей поляризованного света друг на друга», в Crew, 1900, стр. 145–155.
G.-A. Boutry, 1948, «Огюстен Френель: его время, жизнь и работа, 1788–1827», Science Progress , т. 36, № 144 (октябрь 1948 г.), стр. 587–604; jstor.org/stable/43413515.
JZ Buchwald, 1989, Возникновение волновой теории света: оптическая теория и эксперимент в начале девятнадцатого века , Издательство Чикагского университета, ISBN 0-226-07886-8 .
Дж. З. Бухвальд, 2013, «Оптика в девятнадцатом веке», в книге Дж. З. Бухвальда и Р. Фокса (ред.), Оксфордский справочник по истории физики , Оксфорд, ISBN 978-0-19-969625-3 , стр. 445–472.
Х. Крю (ред.), 1900, Волновая теория света: Мемуары Гюйгенса, Юнга и Френеля, American Book Company.
О. Дарригол, 2012, История оптики: от греческой античности до девятнадцатого века , Оксфорд, ISBN 978-0-19-964437-7 .
Дж. Элтон, 2009, «Свет, освещающий нашу тьму: оптика маяка и последующее развитие революционной преломляющей линзы Френеля 1780–1900», Международный журнал по истории техники и технологий , т. 79, № 2 (июль 2009 г.), стр. 183–244; doi : 10.1179/175812109X449612.
Э. Франкель, 1974, «Поиск корпускулярной теории двойного преломления: Малус, Лаплас и ценовая [ sic ] конкуренция 1808 года», Centaurus , т. 18, № 3 (сентябрь 1974 г.), стр. 223–245.
Э. Франкель, 1976, «Корпускулярная оптика и волновая теория света: наука и политика революции в физике», Социальные исследования науки , т. 6, № 2 (май 1976 г.), стр. 141–184; jstor.org/stable/284930.
A. Fresnel, 1815a, Письмо Жану Франсуа «Леонор» Мериме, 10 февраля 1815 г. (Смитсоновская библиотека Дибнера, MSS 546A), напечатано в G. Magalhães, «Замечания о новом автографе письма Огюстена Френеля: аберрация света и теория волн», Science in Context , т. 19, № 2 (июнь 2006 г.), стр. 295–307, doi :10.1017/S0269889706000895, на стр. 306 (оригинальный французский) и стр. 307 (английский перевод).
А. Френель, 1816, «Mémoire sur la diffraction de la lumière» («Воспоминания о дифракции света»), Annales de Chimie et de Physique , сер. 2, том. 1, стр. 239–281 (март 1816 г.); переиздано как «Deuxième Mémoire…» («Вторые мемуары…») во Френеле, 1866–70, том. 1, стр. 89–122. Не путать с более поздними «премиальными мемуарами» (Френель, 1818b).
А. Френель, 1818a, «Mémoire sur les couleurs développées dans les Fluides Homogenes par la lumière Polarisée», прочитано 30 марта 1818 г. (по Кипнису, 1991, стр. 217), опубликовано в 1846 г.; перепечатано во Френеле, 1866–70, т. 1, стр. 655–683; переведено Э. Рональдсом и Х. Ллойдом как «Мемуары о цветах, создаваемых в однородных жидкостях поляризованным светом», в Тейлоре, 1852, стр. 44–65. (Номера страниц относятся к переводу.)
A. Fresnel, 1818b, «Mémoire sur la diffraction de la lumière» («Мемуары о дифракции света»), депонирован 29 июля 1818 г., «коронован» 15 марта 1819 г., опубликован (с приложенными примечаниями) в Mémoires de l'Académie Royale des Sciences de l'Institut de France , т. V (за 1821 и 1822 гг., напечатано в 1826 г.), стр. 339–475; перепечатано (с примечаниями) в Fresnel, 1866–70, т. 1, стр. 247–383; частично переведено как «Премия Френеля о дифракции света», в Crew, 1900 г., стр. 81–144. Не путать с более ранним мемуаром с тем же названием на французском языке (Френель, 1816).
А. Френель, 1818c, «Письмо М. Френеля к М. Араго о влиянии земного движения на Quelques phénomènes d'optique», Annales de Chimie et de Physique , сер. 2, том. 9, стр. 57–66 и табличка после стр. 111 (сентябрь 1818 г.) и стр. 286–287 (ноябрь 1818 г.); перепечатано во Френеле, 1866–70, т. 2, стр. 627–636; переведено как «Письмо Огюстена Френеля Франсуа Араго о влиянии движения Земли на некоторые явления оптики» в К. Ф. Шаффнере, Теории эфира девятнадцатого века , Пергам, 1972 ( doi :10.1016/C2013-0-02335- 3), стр. 125–135; также переведено (с несколькими ошибками) Р. Р. Трейлом как «Письмо Огюстена Френеля Франсуа Араго относительно влияния движения Земли на несколько оптических явлений», General Science Journal , 23 января 2006 г. (PDF, 8 стр.).
А. Френель, 1821a, «Примечание к расчётам тел, которые развиваются в кристаллических пластинках» и далее, Annales de Chimie et de Physique , сер. 2, том. 17, стр. 102–111 (май 1821 г.), 167–196 (июнь 1821 г.), 312–315 («Постскриптум», июль 1821 г.); перепечатано (с добавленными номерами разделов) во Френеле, 1866–70, том. 1, стр. 609–648; переведено как «О расчете оттенков, которые поляризация развивает в кристаллических пластинах, и послесловие», Zenodo : 4058004 / doi :10.5281/zenodo.4058004, 2021.
A. Fresnel, 1821b, «Note sur les remarques de M. Biot...», Annales de Chimie et de Physique , Ser. 2, vol. 17, pp. 393–403 (август 1821 г.); перепечатано (с добавленными номерами разделов) в Fresnel, 1866–70, vol. 1, pp. 601–608; переведено как «Note on the remarks of Mr. Biot related to colors of thin plates», Zenodo : 4541332 / doi :10.5281/zenodo.4541332, 2021.
A. Fresnel, 1821c, Письмо к DFJ Arago, 21 сентября 1821 г., в Fresnel, 1866–70, т. 2, стр. 257–259; переведено как «Письмо к Arago о двуосном двулучепреломлении», Wikisource , апрель 2021 г.
А. Френель, 1822a, Де ла Люмьер ( На свете ), в Ж. Риффо (ред.), Дополнение к французскому переводу де ла cinquième édition du "Système de Chimie" по Th. Томсон, Париж: Chez Méquignon-Marvis, 1822, стр. 1–137, 535–539; перепечатано во Френеле, 1866–70, т. 2, стр. 3–146; переведен Т. Янгом как «Элементарный взгляд на волнообразную теорию света», Ежеквартальный журнал науки, литературы и искусства , том. 22 (январь – июнь 1827 г.), стр. 127–141, 441–454; том. 23 (июль – декабрь 1827 г.), стр. 113–35, 431–448; том. 24 (январь – июнь 1828 г.), стр. 198–215; том. 25 (июль – декабрь 1828 г.), стр. 168–191, 389–407; том. 26 (январь – июнь 1829 г.), стр. 159–165.
A. Fresnel, 1822b, «Mémoire sur un nouveau système d'éclairage des phares», прочитано 29 июля 1822 г.; перепечатано в Fresnel, 1866–70, т. 3, стр. 97–126; переведено T. Tag как «Memoir upon a new system of lighthouse lighting», US Lighthouse Society, просмотрено 26 августа 2017 г.; 19 августа 2016 г. (Указанные номера страниц относятся к переводу.)
A. Fresnel, 1827, "Mémoire sur la double refraction", Mémoires de l'Académie Royale des Sciences de l'Institut de France , т. VII (за 1824 г., напечатано в 1827 г.), стр. 45–176; перепечатано как "Second mémoire…" в Fresnel, 1866–70, т. 2, стр. 479–596; переведено AW Hobson как "Memoir on double refraction", в Taylor, 1852, стр. 238–333. (Указанные номера страниц относятся к переводу. Для заметных опечаток в оригинальном издании, а следовательно, и в переводе, см. Fresnel, 1866–70, т. 2, стр. 596n.)
А. Френель (изд. Х. де Сенармон, Э. Верде и Л. Френель), 1866–70, Oeuvres complètes d'Augustin Fresnel (3 тома), Париж: Imprimerie Impériale; том. 1 (1866), т. 1. 2 (1868), т. 2 (1868 г.), т. 2 (1868 г.), т. 2. 3 (1870 г.).
I. Grattan-Guinness, 1990, Convolutions in French Mathematics, 1800–1840 , Базель: Birkhäuser, т. 2, ISBN 3-7643-2238-1 , глава 13 (стр. 852–915, «Вступление Френеля: Физическая оптика, 1815–1824») и глава 15 (стр. 968–1045, «Вступление Навье и триумф Коши: Теория упругости, 1819–1830»).
C. Huygens, 1690, Traité de la Lumière (Лейден: Van der Aa), переведено SP Thompson как Treatise on Light , University of Chicago Press, 1912; Project Gutenberg, 2005. (Указанные номера страниц соответствуют изданию 1912 года и HTML-изданию Gutenberg.)
FA Jenkins и HE White, 1976, Основы оптики , 4-е изд., Нью-Йорк: McGraw-Hill, ISBN 0-07-032330-5 .
Н. Кипнис, 1991, История принципа интерференции света , Базель: Birkhäuser, ISBN 978-3-0348-9717-4 , главы VII, VIII .
KA Kneller (пер. TM Kettle), 1911, Христианство и лидеры современной науки: вклад в историю культуры в девятнадцатом веке , Фрайбург-им-Брайсгау: B. Herder, стр. 146–149.
TH Levitt, 2009, Тень Просвещения: Оптическая и политическая прозрачность во Франции, 1789–1848 , Оксфорд, ISBN 978-0-19-954470-7 .
TH Levitt, 2013, Короткая яркая вспышка: Огюстен Френель и рождение современного маяка , Нью-Йорк: WW Norton, ISBN 978-0-393-35089-0 .
H. Lloyd, 1834, «Отчет о прогрессе и современном состоянии физической оптики», Отчет Четвертого заседания Британской ассоциации содействия развитию науки (состоявшегося в Эдинбурге в 1834 году), Лондон: J. Murray, 1835, стр. 295–413.
Э. Мах (перевод Дж. С. Андерсона и А. Ф. А. Янга), Принципы физической оптики: историческое и философское рассмотрение , Лондон: Methuen & Co., 1926.
I. Newton, 1730, Opticks: or, a Treatise of the Reflections, Refractions, Inflections, and Colours of Light, 4-е изд. (Лондон: William Innys, 1730; Project Gutenberg, 2010); переиздано с предисловием А. Эйнштейна и введением Э. Т. Уиттекера (Лондон: George Bell & Sons, 1931); переиздано с дополнительным предисловием И. Б. Коэна и аналитическим оглавлением Д. Х. Д. Роллера, Минеола, Нью-Йорк: Дувр, 1952, 1979 (с пересмотренным предисловием), 2012. (Указанные номера страниц соответствуют HTML-изданию Gutenberg и изданиям Дувра.)
RH Silliman, 1967, Augustin Fresnel (1788–1827) and the Establishment of the Wave Theory of Light (диссертация доктора философии, 6 + 352 стр. ), Принстонский университет, подана в 1967 г., принята в 1968 г.; доступно на ProQuest (отсутствует первая страница предисловия).
RH Silliman, 2008, «Френель, Огюстен Жан», Полный словарь научной биографии , Детройт: Charles Scribner's Sons, т. 5, стр. 165–171. (В версии на encyclopedia.com отсутствуют диаграмма и уравнения.)
Р. Тейлор (ред.), 1852, Научные мемуары, выбранные из Трудов иностранных академий наук и ученых обществ, а также из Иностранных журналов (на английском языке), т. V, Лондон: Тейлор и Фрэнсис.
У. Уэвелл, 1857, История индуктивных наук: от самых ранних до настоящих времен , 3-е изд., Лондон: JW Parker & Son, т. 2, книга IX , главы V–XIII .
ET Whittaker , 1910, История теорий эфира и электричества: от эпохи Декарта до конца девятнадцатого века , Лондон: Longmans, Green, & Co., главы IV , V.
J. Worrall, 1989, «Френель, Пуассон и белое пятно: роль успешных предсказаний в принятии научных теорий». Архивировано 2 июня 2023 г. в Wayback Machine , в D. Gooding, T. Pinch и S. Schaffer (ред.), The Uses of Experiment: Studies in the Natural Sciences , Cambridge University Press, ISBN 0-521-33185-4 , стр. 135–157.
Т. Янг, 1807, Курс лекций по натуральной философии и механическим искусствам (2 тома), Лондон: Дж. Джонсон; т. 1, т. 2.
Т. Янг (ред. Г. Пикок), 1855, Разные произведения покойного Томаса Янга , Лондон: Дж. Мюррей, т. 1.

Внешние ссылки

Медиа, связанные с Огюстеном Френелем на Wikimedia Commons

В Викицитатнике есть цитаты, связанные с Огюстеном-Жаном Френелем .

Список английских переводов произведений Огюстена Френеля в Zenodo .
Общество маяков США, в частности «Линзы Френеля, архивировано 2 марта 2021 г. на Wayback Machine ».
Работы Огюстена-Жана Френеля в Открытой библиотеке .
«Эпизод 3 – Огюстен Френель», École polytechnique, 23 января 2019 г., архивировано с оригинала 22 ноября 2021 г. – через YouTube.