Комплексное число

Число с действительной и мнимой частью

Комплексное число можно визуально представить как пару чисел ( a ,  b ) , образующих вектор на диаграмме, называемой диаграммой Аргана , представляющей комплексную плоскость . Re — действительная ось, Im — воображаемая ось, а i — « мнимая единица », удовлетворяющая условию i ² = −1 .

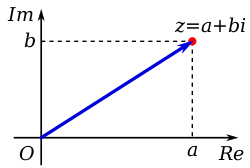
В математике комплексное число — это элемент системы счисления , который расширяет действительные числа конкретным элементом, обозначаемым i , называемым мнимой единицей и удовлетворяющим уравнению ; каждое комплексное число можно выразить в виде , где a и b — действительные числа. Поскольку ни одно действительное число не удовлетворяет приведенному выше уравнению, Рене Декарт назвал меня мнимым числом . Для комплексного числа а называется ${\displaystyle i^{2}=-1}$ ${\displaystyle a+bi}$ ${\displaystyle a+bi}$ действительная часть , аbназываетсямнимая часть . Множество комплексных чисел обозначается либо символом,либо C. Несмотря на историческую номенклатуру «мнимых», комплексные числа считаются вматематических наукахтакими же «реальными», как и действительные числа, и имеют фундаментальное значение во многих аспектах научного описания мира природы. ^[1][а] ${\displaystyle \mathbb {C} }$

Комплексные числа позволяют найти решение всех полиномиальных уравнений , даже тех, которые не имеют решений в действительных числах. Точнее, основная теорема алгебры утверждает, что каждое непостоянное полиномиальное уравнение с действительными или комплексными коэффициентами имеет решение, которое является комплексным числом. Например, уравнение не имеет действительного решения, поскольку квадрат действительного числа не может быть отрицательным, но имеет два недействительных комплексных решения и . ${\displaystyle (x+1)^{2}=-9}$ ${\displaystyle -1+3i}$ ${\displaystyle -1-3i}$

Сложение, вычитание и умножение комплексных чисел можно естественным образом определить, используя правило в сочетании с ассоциативными , коммутативными и распределительными законами . Каждое ненулевое комплексное число имеет обратное мультипликативное число . Это делает комплексные числа полем , подполем которого являются действительные числа. Комплексные числа также образуют вещественное векторное пространство размерности два со стандартным базисом {1, i } . ${\displaystyle i^{2}=-1}$

Этот стандартный базис превращает комплексные числа в декартову плоскость , называемую комплексной плоскостью . Это позволяет геометрическую интерпретацию комплексных чисел и операций с ними и, наоборот, выражать через комплексные числа некоторые геометрические свойства и конструкции. Например, действительные числа образуют действительную линию , отождествляемую с горизонтальной осью комплексной плоскости. Комплексные числа с абсолютным значением один образуют единичный круг . Сложение комплексного числа — это перенос в комплексной плоскости, а умножение на комплексное число — это подобие с центром в начале координат. Комплексное сопряжение представляет собой зеркальную симметрию относительно вещественной оси. Комплексное абсолютное значение является евклидовой нормой .

Таким образом, комплексные числа образуют богатую структуру, которая одновременно является алгебраически замкнутым полем , коммутативной алгеброй над действительными числами и евклидовым векторным пространством размерности два.

Определение

Иллюстрация комплексного числа z = x + iy на комплексной плоскости . Действительная часть — это x , а мнимая часть — y .

Комплексное число — это число вида a + bi , где a и b — действительные числа , а i — неопределенное число, удовлетворяющее i ² = −1 . Например, 2 + 3 i — комплексное число. ^[3]

Таким образом, комплексное число определяется как многочлен с действительными коэффициентами при единственном неопределенном i , для которого налагается соотношение i ² + 1 = 0 . Основываясь на этом определении, комплексные числа можно складывать и умножать, используя сложение и умножение многочленов. Отношение i ² + 1 = 0 индуцирует равенства i ^{4 k} = 1, i ^{4 k +1} = i , i ^{4 k +2} = −1 и i ^{4 k +3} = − i , которые справедливы для всех целых k ; они позволяют свести любой многочлен, полученный в результате сложения и умножения комплексных чисел, к линейному многочлену от i , опять же формы a + bi с действительными коэффициентами a, b.

Действительное число a называется действительной частью комплексного числа a + bi ; действительное число b называется его мнимой частью . Подчеркнем, что мнимая часть не включает в себя коэффициент i ; то есть мнимая часть равна b , а не bi . ^{[4] [5]}

Формально комплексные числа определяются как фактор-кольцо кольца многочленов от неопределенного i по идеалу , порожденному многочленом i ² + 1 (см. ниже). ^[6]

Обозначения

Действительное число a можно рассматривать как комплексное число a + 0 i , мнимая часть которого равна 0. Чисто мнимое число bi — это комплексное число 0 + bi , действительная часть которого равна нулю. Как и в случае с полиномами, принято писать a вместо a + 0 i и bi вместо 0 + bi . Более того, когда мнимая часть отрицательна, т. е. b = − |b| < 0 , обычно пишут a − |b|i вместо a + (− |b| ) i ; например, для b = −4 , 3 − 4 i можно написать вместо 3 + (−4) i .

Поскольку умножение неопределенного i и вещественного числа коммутативно в многочленах с действительными коэффициентами, многочлен a + bi можно записать как a + ib . Это часто целесообразно для мнимых частей, обозначаемых выражениями, например, когда b — радикал. ^[7]

Действительная часть комплексного числа z обозначается Re( z ) , , или ; мнимая часть комплексного числа z обозначается Im( z ) , , или Например, ${\displaystyle {\mathcal {Re}}(z)}$ ${\displaystyle {\mathfrak {R}}(z)}$ ${\displaystyle {\mathcal {Im}}(z)}$ ${\displaystyle {\mathfrak {I}}(z).}$

$${\displaystyle \operatorname {Re} (2+3i)=2\quad {\text{ and }}\quad \operatorname {Im} (2+3i)=3~.}$$

Набор всех комплексных чисел обозначается ( жирный шрифт на доске ) или C (жирный вертикальный шрифт). ${\displaystyle \mathbb {C} }$

В некоторых дисциплинах, особенно в электромагнетизме и электротехнике , вместо i используется j , поскольку i часто используется для обозначения электрического тока . ^{[8] [9]} В этих случаях комплексные числа записываются как a + bj или a + jb .

Визуализация

Комплексное число z в виде точки (черный) и вектора ее положения (синий).

Таким образом, комплексное число z можно отождествить с упорядоченной парой действительных чисел, которые, в свою очередь, можно интерпретировать как координаты точки в двумерном пространстве. Самым ближайшим пространством является евклидова плоскость с подходящими координатами, которую затем называют комплексной плоскостью или диаграммой Аргана , ^{[10] [б] [11]} имени Жана-Робера Аргана . Другое известное пространство, на которое можно проецировать координаты, — это двумерная поверхность сферы, которую тогда называют сферой Римана . ${\displaystyle (\Re (z),\Im (z))}$

Декартова комплексная плоскость

Определение комплексных чисел, включающих два произвольных действительных значения, сразу предполагает использование декартовых координат в комплексной плоскости. Горизонтальная ( действительная ) ось обычно используется для отображения действительной части с возрастающими значениями вправо, а мнимая часть отмечает вертикальную ( мнимую ) ось с возрастающими значениями вверх.

Число на карте можно рассматривать либо как координатированную точку, либо как вектор положения от начала координат до этой точки. Следовательно , значения координат комплексного числа z могут быть выражены в декартовой , прямоугольной или алгебраической форме.

Примечательно, что операции сложения и умножения приобретают вполне естественный геометрический характер, когда комплексные числа рассматриваются как векторы положения: сложение соответствует сложению векторов , а умножение (см. ниже) соответствует умножению их величин и сложению углов, образуемых ими с реальная ось. С этой точки зрения умножение комплексного числа на i соответствует повороту вектора положения против часовой стрелки на четверть оборота ( 90° ) вокруг начала координат — факт, который можно выразить алгебраически как

$${\displaystyle (x+yi)\,i=-y+xi.}$$

Полярный комплексный самолет

Модуль и аргумент

Аргумент φ и модуль r определяют точку на комплексной плоскости.

Альтернативным вариантом координат на комплексной плоскости является полярная система координат , которая использует расстояние точки z от начала координат ( O ) и угол, образуемый между положительной действительной осью и отрезком линии Oz в направлении против часовой стрелки. Это приводит к полярной форме

${\displaystyle z=re^{i\varphi }=r(\cos \varphi +i\sin \varphi )}$

комплексного числа , где r — абсолютное значение z и аргумент z . ${\displaystyle \varphi }$

Абсолютное значение (или модуль или величина ) комплексного числа z = x + yi равно ^[12]

$${\displaystyle r=|z|={\sqrt {x^{2}+y^{2}}}.}$$

zy = 0r = | х |

По теореме Пифагора абсолютное значение комплексного числа — это расстояние до начала координат точки, представляющей комплексное число на комплексной плоскости .

Аргумент z (во многих приложениях называемый «фазой» φ ) ^{[11] представляет} собой угол радиуса Oz с положительной действительной осью и записывается как arg z . Как и в случае с модулем, аргумент можно найти из прямоугольной формы x + yi ^[13] путем применения обратного тангенса к фактору мнимых и действительных частей. Используя тождество половинного угла, одной ветви арктанса достаточно, чтобы охватить диапазон (− π , π ] arg -функции , и позволяет избежать более тонкого анализа каждого конкретного случая.

$${\displaystyle \varphi =\arg(x+yi)={\begin{cases}2\arctan \left({\dfrac {y}{x+{\sqrt {x^{2}+y^{2}}}}}\right)&{\text{if }}y\neq 0{\text{ or }}x>0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}}$$

Обычно, как указано выше, выбирается главное значение в интервале (− π , π ) . Если значение arg отрицательное, значения в диапазоне (− π , π ] или [0, 2 π ) можно получить путем сложения 2 π . В этой статье значение φ выражается в радианах . Оно может увеличиваться на любое целое число, кратное 2 π , и при этом давать тот же угол, рассматриваемый как стянутый лучами положительной действительной оси и от начала координат через z . Следовательно, arg-функция иногда рассматривается как многозначная Полярный угол для комплексного числа 0 неопределенен, но произвольный выбор полярного угла 0 является обычным явлением.

Значение φ равно результату atan2 :

$${\displaystyle \varphi =\operatorname {atan2} \left(\operatorname {Im} (z),\operatorname {Re} (z)\right).}$$

Вместе r и φ дают другой способ представления комплексных чисел, полярную форму , поскольку комбинация модуля и аргумента полностью определяет положение точки на плоскости. Восстановление исходных прямоугольных координат из полярной формы осуществляется по формуле, называемой тригонометрической формой.

$${\displaystyle z=r(\cos \varphi +i\sin \varphi ).}$$

Используя формулу Эйлера, это можно записать как

$${\displaystyle z=re^{i\varphi }{\text{ or }}z=r\exp i\varphi .}$$

Используя функцию цис , это иногда сокращается до

$${\displaystyle z=r\operatorname {\mathrm {cis} } \varphi .}$$

В угловом обозначении , часто используемом в электронике для представления вектора с амплитудой r и фазой φ , оно записывается как ^[14]

$${\displaystyle z=r\angle \varphi .}$$

Сложные графики

График цветового круга выражения( z ² - 1)( z - 2 - я ) ²/z ² + 2 + 2 я

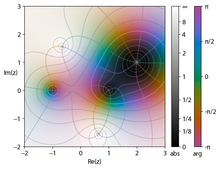
При визуализации сложных функций необходимы как сложные входные, так и выходные данные. Поскольку каждое комплексное число представлено в двух измерениях, для визуального построения графика сложной функции потребуется восприятие четырехмерного пространства , что возможно только в проекциях. По этой причине были разработаны другие способы визуализации сложных функций.

При раскрашивании доменов выходные размеры представлены цветом и яркостью соответственно. Каждая точка на комплексной плоскости как домен украшена орнаментом , обычно цветом, представляющим аргумент комплексного числа, и яркостью , представляющей величину. Темные пятна отмечают модули, близкие к нулю, более яркие пятна находятся дальше от начала координат, градация может быть прерывистой, но считается монотонной. Цвета часто варьируются с шагомπ/3от 0 до 2 π от красного, желтого, зеленого, голубого, синего до пурпурного. Эти графики называются графиками цветового круга . Это обеспечивает простой способ визуализации функций без потери информации. На рисунке показаны нули для ±1, (2 + i ) и полюса в точках ${\displaystyle \pm {\sqrt {-2-2i}}.}$

История

Решение в радикалах (без тригонометрических функций ) общего кубического уравнения , когда все три его корня являются действительными числами, содержит квадратные корни из отрицательных чисел , ситуацию, которую нельзя исправить путем факторизации с помощью теста на рациональный корень , если кубическая неприводима ; это так называемый casus reducibilis («неприводимый случай»). Эта загадка привела к тому, что итальянский математик Джероламо Кардано примерно в 1545 году в своей книге «Ars Magna» придумал комплексные числа ^[15] , хотя его понимание было рудиментарным; более того, позже он описал комплексные числа как «настолько тонкие, насколько и бесполезные». ^[16] Кардано действительно использовал воображаемые числа, но назвал их «психической пыткой». ^[17] Это было до использования графической сложной плоскости. Кардано и другие итальянские математики, особенно Сципионе дель Ферро , в 1500-х годах создали алгоритм решения кубических уравнений, которые обычно имели одно действительное решение и два решения, содержащие мнимое число. Поскольку они игнорировали ответы с мнимыми числами, Кардано счел их бесполезными. ^[18]

Работа над проблемой общих полиномов в конечном итоге привела к фундаментальной теореме алгебры , которая показывает, что с комплексными числами решение существует для каждого полиномиального уравнения степени один или выше. Таким образом, комплексные числа образуют алгебраически замкнутое поле , где любое полиномиальное уравнение имеет корень .

Многие математики внесли свой вклад в разработку комплексных чисел. Правила сложения, вычитания, умножения и извлечения корня комплексных чисел разработал итальянский математик Рафаэль Бомбелли . ^[19] Более абстрактный формализм для комплексных чисел был далее развит ирландским математиком Уильямом Роуэном Гамильтоном , который распространил эту абстракцию на теорию кватернионов . ^[20]

Самое раннее мимолетное упоминание о квадратных корнях из отрицательных чисел , возможно, встречается в работе греческого математика Героя Александрийского в I веке нашей эры , где в своей «Стереометрике» он рассматривал, по-видимому, по ошибке, объем невозможного усеченного пирамидального круга . пирамиду , чтобы получить термин в своих расчетах, который сегодня можно было бы упростить до . ^[c] Отрицательные величины не были поняты в эллинистической математике , и Герой просто заменил их положительными ^[22] ${\displaystyle {\sqrt {81-144}}}$ ${\displaystyle {\sqrt {-63}}=3i{\sqrt {7}}}$ ${\displaystyle {\sqrt {144-81}}=3{\sqrt {7}}.}$

Стимул к изучению комплексных чисел как отдельной темы впервые возник в 16 веке, когда итальянские математики ( Никколо Фонтана Тарталья и Джероламо Кардано ) обнаружили алгебраические решения для корней многочленов кубической и четвертой степени . Вскоре стало понятно (но было доказано гораздо позже) ^[23] , что эти формулы, даже если интересовались только действительными решениями, иногда требуют манипуляций с квадратными корнями из отрицательных чисел. Фактически позже было доказано, что использование комплексных чисел неизбежно , когда все три корня вещественны и различны. ^[d] Однако в этом случае все же можно использовать общую формулу, с некоторой осторожностью, чтобы справиться с двусмысленностью, возникающей из-за существования трех кубических корней для ненулевых комплексных чисел. Рафаэль Бомбелли был первым, кто открыто обратился к этим, казалось бы, парадоксальным решениям кубических уравнений и разработал правила комплексной арифметики, пытаясь решить эти проблемы.

Термин «мнимые» для этих величин был введен Рене Декартом в 1637 году, который изо всех сил старался подчеркнуть их нереальную природу: ^[24]

... иногда только воображаемые, то есть можно представить столько, сколько я сказал в каждом уравнении, но иногда не существует количества, соответствующего тому, которое мы воображаем.
[ ... quelquefois seulement imaginaires c'est-a-dire que l'on peut toujours en Imagine autant que j'ai dit en chaque équation, но больше, чем qu'il n'y a quelquefois aucune quantité qui, соответствует à celle qu'on представлять себе. ]

Еще одним источником путаницы было то, что уравнение казалось причудливо несовместимым с алгебраическим тождеством , которое справедливо для неотрицательных действительных чисел a и b и которое также использовалось в вычислениях комплексных чисел с одним из a , b положительным и другой негатив. Неверное использование этого тождества в случае, когда и a , и b отрицательны, и связанное с ним тождество смутило даже Леонарда Эйлера . Эта трудность в конечном итоге привела к тому, что во избежание этой ошибки было принято использовать специальный символ i вместо . ^{[ нужна цитата ]} Несмотря на это, Эйлер считал естественным знакомить студентов с комплексными числами гораздо раньше, чем мы это делаем сегодня. В своем учебнике элементарной алгебры « Элементы алгебры » он почти сразу вводит эти числа, а затем использует их естественным образом повсюду. ${\displaystyle {\sqrt {-1}}^{2}={\sqrt {-1}}{\sqrt {-1}}=-1}$ ${\displaystyle {\sqrt {a}}{\sqrt {b}}={\sqrt {ab}}}$ ${\textstyle {\frac {1}{\sqrt {a}}}={\sqrt {\frac {1}{a}}}}$ ${\displaystyle {\sqrt {-1}}}$

В 18 веке комплексные числа получили более широкое использование, поскольку было замечено, что формальные манипуляции со сложными выражениями можно использовать для упрощения вычислений с использованием тригонометрических функций. Например, в 1730 году Абрахам де Муавр заметил, что тождества, связывающие тригонометрические функции целого числа, кратного углу, со степенями тригонометрических функций этого угла, могут быть перевыражены следующей формулой Муавра :

$${\displaystyle (\cos \theta +i\sin \theta )^{n}=\cos n\theta +i\sin n\theta .}$$

В 1748 году Эйлер пошел дальше и получил формулу комплексного анализа Эйлера : ^[25]

$${\displaystyle \cos \theta +i\sin \theta =e^{i\theta }}$$

формально манипулируя сложными степенными рядами , и заметил, что эту формулу можно использовать для сведения любого тригонометрического тождества к гораздо более простым экспоненциальным тождествам.

Идея комплексного числа как точки на комплексной плоскости (вверху) была впервые описана датско - норвежским математиком Каспаром Весселем в 1799 году, ^[26] хотя она была предсказана еще в 1685 году в « Трактате по алгебре» Уоллиса . ^[27]

Мемуары Весселя появились в журнале Proceedings of the Copenhagen Academy , но остались практически незамеченными. В 1806 году Жан-Робер Арган независимо выпустил брошюру о комплексных числах и предоставил строгое доказательство основной теоремы алгебры . ^[28] Карл Фридрих Гаусс ранее опубликовал по существу топологическое доказательство теоремы в 1797 году, но тогда выразил свои сомнения относительно «истинной метафизики квадратного корня из −1». ^[29] Лишь в 1831 году он преодолел эти сомнения и опубликовал свой трактат о комплексных числах как точках на плоскости, ^[30] в значительной степени установив современные обозначения и терминологию: ^[31]

Если раньше кто-то рассматривал этот предмет с ложной точки зрения и потому обнаруживал таинственную тьму, то это во многом объясняется неуклюжей терминологией. Если бы не называли +1, -1, положительные, отрицательные или мнимые (или даже невозможные) единицы, а, скажем, прямые, обратные или латеральные единицы, то о такой тьме вряд ли могла бы идти речь. ${\displaystyle {\sqrt {-1}}}$

В начале 19 века другие математики независимо открыли геометрическое представление комплексных чисел: Буэ, ^{[32] [33]} Мури , ^[34] Уоррен, ^{[35] [36] [37]} Франсэ и его брат Беллавитис . . ^{[38] [39]}

Английский математик Г.Х. Харди заметил, что Гаусс был первым математиком, который использовал комплексные числа «по-настоящему уверенно и научно», хотя такие математики, как норвежский Нильс Хенрик Абель и Карл Густав Якоб Якоби, обязательно использовали их регулярно до того, как Гаусс опубликовал свой трактат 1831 года. ^[40]

Огюстен-Луи Коши и Бернхард Риман вместе довели фундаментальные идеи комплексного анализа до высокой степени завершенности, начиная примерно с 1825 года в случае Коши.

Общие термины, используемые в теории, в основном принадлежат ее основателям. Арган назвал cos φ + i sin φ коэффициентом направления и модулем ; ^{[e] [41]} Коши (1821) назвал cos φ + i sin φ приведенной формой (l'expression reduite) ^[42] и, по-видимому, ввёл термин аргумент ; Гаусс использовал i вместо , ^[f] ввёл термин комплексное число для a + bi , ^[g] и назвал a ² + b ² нормой . ^[h] Коэффициент направления выражения , часто используемый для cos φ + i sin φ , принадлежит Ханкелю (1867), ^[46] , а абсолютное значение для модуля принадлежит Вейерштрассу. ${\displaystyle r={\sqrt {a^{2}+b^{2}}}}$ ${\displaystyle {\sqrt {-1}}}$

К более поздним классическим авторам общей теории относятся Рихард Дедекинд , Отто Гёльдер , Феликс Кляйн , Анри Пуанкаре , Герман Шварц , Карл Вейерштрасс и многие другие. Важные работы (в том числе по систематизации) в области комплексного многомерного исчисления были начаты в начале 20 века. Важные результаты были достигнуты Вильгельмом Виртингером в 1927 году.

Отношения и операции

Равенство

Комплексные числа имеют такое же определение равенства, что и действительные числа; два комплексных числа a ₁ + b ₁ i и a ₂ + b ₂ i равны тогда и только тогда, когда равны их действительная и мнимая части, то есть если a ₁ = a ₂ и b ₁ = b ₂ . Ненулевые комплексные числа, записанные в полярной форме, равны тогда и только тогда, когда они имеют одинаковую величину и их аргументы отличаются на целое число, кратное 2 π .

Заказ

В отличие от действительных чисел, комплексные числа не имеют естественного порядка. В частности, не существует линейного порядка комплексных чисел, совместимого со сложением и умножением. Следовательно, комплексные числа не имеют структуры упорядоченного поля. Одно из объяснений этого состоит в том, что каждая нетривиальная сумма квадратов в упорядоченном поле отлична от нуля, а i ² + 1 ² = 0 — нетривиальная сумма квадратов. Таким образом, комплексные числа естественным образом считаются существующими в двумерной плоскости.

Сопряженный

Геометрическое представление z и сопряженного с ним z в комплексной плоскости

Комплексно -сопряженное число z = x + yi определяется как x − yi . Он обозначается либо z , либо z * . ^[47] Эту унарную операцию над комплексными числами невозможно выразить, применяя только их основные операции сложения, вычитания, умножения и деления.

Геометрически z является « отражением» z относительно реальной оси. Двойное сопряжение дает исходное комплексное число.

$${\displaystyle {\overline {\overline {z}}}=z,}$$

что делает эту операцию инволюцией . Отражение оставляет неизменными как действительную часть, так и величину z , т.е.

$${\displaystyle \operatorname {Re} ({\overline {z}})=\operatorname {Re} (z)\quad }$$

${\displaystyle \quad |{\overline {z}}|=|z|.}$

Мнимая часть и аргумент комплексного числа z меняют знак при сопряжении

$${\displaystyle \operatorname {Im} ({\overline {z}})=-\operatorname {Im} (z)\quad {\text{ and }}\quad \operatorname {arg} {\overline {z}}\equiv -\operatorname {arg} z{\pmod {2\pi }}.}$$

Подробную информацию об аргументе и величине см. в разделе «Полярная форма».

Произведение комплексного числа z = x + yi и его сопряженного числа называется абсолютным квадратом . Это всегда неотрицательное действительное число, равное квадрату величины каждого из них:

$${\displaystyle z\cdot {\overline {z}}=x^{2}+y^{2}=|z|^{2}=|{\overline {z}}|^{2}.}$$

Это свойство можно использовать для преобразования дроби с комплексным знаменателем в эквивалентную дробь с действительным знаменателем путем расширения числителя и знаменателя дроби на сопряженное к данному знаменателю число. Этот процесс иногда называют « рационализацией » знаменателя (хотя знаменатель в конечном выражении может быть иррациональным действительным числом), поскольку он напоминает метод удаления корней из простых выражений в знаменателе.

Действительную и мнимую части комплексного числа z можно извлечь с помощью сопряжения:

$${\displaystyle \operatorname {Re} (z)={\dfrac {z+{\overline {z}}}{2}},\quad {\text{ and }}\quad \operatorname {Im} (z)={\dfrac {z-{\overline {z}}}{2i}}.}$$

Сопряжение распределяет по основным сложным арифметическим действиям:

$${\displaystyle {\begin{aligned}{\overline {z\pm w}}&={\overline {z}}\pm {\overline {w}},\\{\overline {z\cdot w}}&={\overline {z}}\cdot {\overline {w}},\\{\overline {z/w}}&={\overline {z}}/{\overline {w}}.\end{aligned}}}$$

Сопряжение также используется в инверсной геометрии — разделе геометрии, изучающем более общие отражения, чем отражения относительно прямой. В сетевом анализе электрических цепей комплексное сопряжение используется для нахождения эквивалентного импеданса, когда ищется теорема о максимальной передаче мощности .

Сложение и вычитание

Сложение двух комплексных чисел можно выполнить геометрически, построив параллелограмм.

Два комплексных числа легче всего сложить , сложив по отдельности их действительную и мнимую части. То есть: ${\displaystyle a=x+yi}$ ${\displaystyle b=u+vi}$

$${\displaystyle a+b=(x+yi)+(u+vi)=(x+u)+(y+v)i.}$$

вычитание

$${\displaystyle a-b=(x+yi)-(u+vi)=(x-u)+(y-v)i.}$$

Умножение комплексного числа и действительного числа r можно выполнить аналогичным образом, умножив отдельно r , а также действительную и мнимую части a : ${\displaystyle a=x+yi}$

$${\displaystyle ra=r(x+yi)=rx+ryi.}$$

вычитаемое-1уменьшаемому

$${\displaystyle a-b=a+(-1)\,b.}$$

Используя визуализацию комплексных чисел на комплексной плоскости, сложение имеет следующую геометрическую интерпретацию: сумма двух комплексных чисел a и b , интерпретируемых как точки на комплексной плоскости, представляет собой точку, полученную путем построения параллелограмма из трех вершин O , и точки стрелок, обозначенные a и b (при условии, что они не лежат на одной прямой). Эквивалентно, назвав эти точки A , B соответственно и четвертой точкой параллелограмма X , треугольники OAB и XBA конгруэнтны .

Умножение и квадрат

Правила распределительного свойства , коммутативных свойств (сложения и умножения) и определяющего свойства i ² = −1 применяются к комплексным числам. Следует, что

$${\displaystyle (x+yi)\,(u+vi)=(xu-yv)+(xv+yu)i.}$$

В частности,

$${\displaystyle (x+yi)^{2}=x^{2}-y^{2}+2xyi.}$$

Взаимное и деление

Используя сопряжение, обратную величину ненулевого комплексного числа можно разбить на действительную и мнимую компоненты. ${\displaystyle z=x+yi}$

$${\displaystyle {\frac {1}{z}}={\frac {\bar {z}}{z{\bar {z}}}}={\frac {\bar {z}}{|z|^{2}}}={\frac {x-yi}{x^{2}+y^{2}}}={\frac {x}{x^{2}+y^{2}}}-{\frac {y}{x^{2}+y^{2}}}i.}$$

Это можно использовать для выражения деления произвольного комплексного числа на ненулевое комплексное число как ${\displaystyle w=u+vi}$ ${\displaystyle z=x+yi}$

$${\displaystyle {\frac {w}{z}}={\frac {w{\bar {z}}}{|z|^{2}}}={\frac {(u+vi)(x-iy)}{x^{2}+y^{2}}}={\frac {ux+vy}{x^{2}+y^{2}}}+{\frac {vx-uy}{x^{2}+y^{2}}}i.}$$

Умножение и деление в полярной форме

Умножение 2 + i (синий треугольник) и 3 + i (красный треугольник). Красный треугольник поворачивается так, чтобы соответствовать вершине синего треугольника (сложение обоих углов в терминах φ ₁ + φ ₂ в уравнении) и растягивается на длину гипотенузы синего треугольника (умножение обоих радиусов, согласно члену r ₁ r ₂ в уравнении).

Формулы умножения, деления и возведения в степень в полярной форме проще, чем соответствующие формулы в декартовых координатах. Учитывая два комплексных числа z ₁ = r ₁ (cos  φ ₁ + i  sin  φ ₁ ) и z ₂ = r ₂ (cos  φ ₂ + i  sin  φ ₂ ) , в силу тригонометрических тождеств

$${\displaystyle {\begin{alignedat}{4}\cos a\cos b&-\sin a\sin b&{}={}&\cos(a+b)\\\cos a\sin b&+\sin a\cos b&{}={}&\sin(a+b).\end{alignedat}}}$$

мы можем вывести

$${\displaystyle z_{1}z_{2}=r_{1}r_{2}(\cos(\varphi _{1}+\varphi _{2})+i\sin(\varphi _{1}+\varphi _{2})).}$$

iоборотаi ² = −1

$${\displaystyle (2+i)(3+i)=5+5i.}$$

5 + 5 iπ /4радианахарктансу

$${\displaystyle {\frac {\pi }{4}}=\arctan \left({\frac {1}{2}}\right)+\arctan \left({\frac {1}{3}}\right)}$$

арктангаформулы Мачинаπ

Аналогично деление определяется выражением

$${\displaystyle {\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\left(\cos(\varphi _{1}-\varphi _{2})+i\sin(\varphi _{1}-\varphi _{2})\right).}$$

Квадратный корень

Квадратные корни из a + bi (при b ≠ 0 ) равны , где ${\displaystyle \pm (\gamma +\delta i)}$

$${\displaystyle \gamma ={\sqrt {\frac {a+{\sqrt {a^{2}+b^{2}}}}{2}}}}$$

и

$${\displaystyle \delta =(\operatorname {sgn} b){\sqrt {\frac {-a+{\sqrt {a^{2}+b^{2}}}}{2}}},}$$

где Signum — функция Signum . Это можно увидеть, возведя в квадрат, чтобы получить a + bi . ^[48] ​​[ ^49] Здесь называется модулем a + bi , а знак квадратного корня указывает на квадратный корень с неотрицательной действительной частью, называемый главным квадратным корнем ; также где z = a + bi . ^[50] ${\displaystyle \pm (\gamma +\delta i)}$ ${\displaystyle {\sqrt {a^{2}+b^{2}}}}$ ${\displaystyle {\sqrt {a^{2}+b^{2}}}={\sqrt {z{\overline {z}}}},}$

Экспоненциальная функция

Показательную функцию можно определить для каждого комплексного числа z степенным рядом ${\displaystyle \exp \colon \mathbb {C} \to \mathbb {C} ;z\mapsto \exp z}$

$${\displaystyle \exp z=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}},}$$

радиус сходимости

Значение 1 экспоненциальной функции - это число Эйлера.

$${\displaystyle e=\exp 1=\sum _{n=0}^{\infty }{\frac {1}{n!}}\approx 2.71828.}$$

zаналитическое продолжениеze ${\displaystyle \exp z=e^{z}.}$

$${\displaystyle e^{z}=\exp z.}$$

Функциональное уравнение

Показательная функция удовлетворяет функциональному уравнению. Это можно доказать либо путем сравнения разложения обоих членов в степенной ряд, либо путем применения аналитического продолжения ограничения уравнения на действительные аргументы. ${\displaystyle e^{z+t}=e^{z}e^{t}.}$

Формула Эйлера

Формула Эйлера утверждает , что для любого действительного числа y

$${\displaystyle e^{iy}=\cos y+i\sin y.}$$

Таким образом, из функционального уравнения следует, что если x и y действительны, то

$${\displaystyle e^{x+iy}=e^{x}(\cos y+i\sin y)=e^{x}\cos y+ie^{x}\sin y,}$$

Комплексный логарифм

В реальном случае натуральный логарифм можно определить как обратную показательную функцию. Чтобы распространить это на комплексную область, можно начать с формулы Эйлера. Это означает, что если комплексное число записано в полярной форме ${\displaystyle \ln \colon \mathbb {R} ^{+}\to \mathbb {R} ;x\mapsto \ln x}$ ${\displaystyle z\in \mathbb {C} ^{\times }}$

$${\displaystyle z=r(\cos \varphi +i\sin \varphi )}$$

${\displaystyle r,\varphi \in \mathbb {R} ,}$

$${\displaystyle \ln z=\ln r+i\varphi }$$

комплексный логарифм

$${\displaystyle \exp \ln z=\exp(\ln r+i\varphi )=r\exp i\varphi =r(\cos \varphi +i\sin \varphi )=z.}$$

Однако, поскольку косинус и синус являются периодическими функциями, добавление целого числа, кратного 2 π , к φ не меняет z . Например, e ^iπ = e ^{3 iπ} = −1 , поэтому и iπ , и 3 iπ являются возможными значениями натурального логарифма −1 .

Следовательно, если комплексный логарифм не следует определять как многозначную функцию

$${\displaystyle \ln z=\left\{\ln r+i(\varphi +2\pi k)\mid k\in \mathbb {Z} \right\},}$$

разрез веткикодоменбиективной

$${\displaystyle \ln \colon \;\mathbb {C} ^{\times }\;\to \;\;\;\mathbb {R} ^{+}+\;i\,\left(-\pi ,\pi \right].}$$

Если это не положительное действительное число (положительное или недействительное число), результирующее главное значение комплексного логарифма получается с − π < φ < π . Это аналитическая функция вне отрицательных действительных чисел, но ее нельзя продолжить до функции, непрерывной при любом отрицательном вещественном числе , где главное значение равно ln z = ln(− z ) + iπ . ^[я] ${\displaystyle z\in \mathbb {C} \setminus \left(-\mathbb {R} _{\geq 0}\right)}$ ${\displaystyle z\in -\mathbb {R} ^{+}}$

Возведение в степень

Если x > 0 вещественное, а z комплексное, возведение в степень определяется как

$${\displaystyle x^{z}=e^{z\ln x},}$$

ln

Кажется естественным распространить эту формулу на комплексные значения x , но возникают некоторые трудности, связанные с тем, что комплексный логарифм на самом деле является не функцией, а многозначной функцией .

Отсюда следует, что если z такое же, как указано выше, и если t — другое комплексное число, то возведение в степень — это многозначная функция.

$${\displaystyle z^{t}=\left\{e^{t(\ln r+i(\varphi +2\pi k))}\mid k\in \mathbb {Z} \right\}}$$

Целые и дробные показатели степени

Геометрическое представление корней со 2-й по 6-ю комплексного числа z в полярной форме re ^iφ  , где r = | г  | и φ = arg z . Если z действительно, φ = 0 или π . Главные корни показаны черным цветом.

Если в предыдущей формуле t — целое число, то синус и косинус не зависят от k . Таким образом, если показатель степени n является целым числом, то z ⁿ корректно определен, и формула возведения в степень упрощается до формулы Муавра :

$${\displaystyle z^{n}=(r(\cos \varphi +i\sin \varphi ))^{n}=r^{n}\,(\cos n\varphi +i\sin n\varphi ).}$$

Корни n -й степени комплексного числа z имеют вид

$${\displaystyle z^{1/n}={\sqrt[{n}]{r}}\left(\cos \left({\frac {\varphi +2k\pi }{n}}\right)+i\sin \left({\frac {\varphi +2k\pi }{n}}\right)\right)}$$

0 ≤ k ≤ п - 1n-rk ${\displaystyle {\sqrt[{n}]{r}}}$

Хотя корень n- й степени положительного действительного числа r выбирается в качестве положительного действительного числа c, удовлетворяющего c ⁿ = r , не существует естественного способа отличить один конкретный комплексный корень n- й степени комплексного числа. Следовательно, корень n- й степени является n -значной функцией от z . Это означает, что, в отличие от случая положительных действительных чисел, имеем

$${\displaystyle (z^{n})^{1/n}\neq z,}$$

n

Характеристики

Структура поля

Набор комплексных чисел представляет собой поле . ^[51] Вкратце, это означает, что справедливы следующие факты: во-первых, любые два комплексных числа можно сложить и умножить, чтобы получить другое комплексное число. Во-вторых, для любого комплексного числа z его обратное аддитивное число — z также является комплексным числом; и в-третьих, каждое ненулевое комплексное число имеет обратное комплексное число. Более того, эти операции удовлетворяют ряду законов, например закону коммутативности сложения и умножения любых двух комплексных чисел z ₁ и z ₂ : ${\displaystyle \mathbb {C} }$

$${\displaystyle {\begin{aligned}z_{1}+z_{2}&=z_{2}+z_{1},\\z_{1}z_{2}&=z_{2}z_{1}.\end{aligned}}}$$

В отличие от действительных чисел, это не упорядоченное поле , то есть невозможно определить отношение z ₁ < z ₂ , совместимое со сложением и умножением. Фактически, в любом упорядоченном поле квадрат любого элемента обязательно положителен, поэтому i ² = −1 исключает существование упорядочения в [ ^52] ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} .}$

Если базовым полем математической темы или конструкции является поле комплексных чисел, название темы обычно изменяется, чтобы отразить этот факт. Например: комплексный анализ , комплексная матрица , комплексный полином и комплексная алгебра Ли .

Решения полиномиальных уравнений

Учитывая любые комплексные числа (называемые коэффициентами ) a ₀ , ...,  an , _{уравнение}

$${\displaystyle a_{n}z^{n}+\dotsb +a_{1}z+a_{0}=0}$$

za ₁ , ...,  an _не^[6]теоремы алгебрыФридриха ГауссаЖана ле Рона д'Аламбераалгебраически замкнутымполя рациональных чиселx ² − 2√2x ² + 4xx ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {R} }$

Существуют различные доказательства этой теоремы либо аналитическими методами, такими как теорема Лиувилля , либо топологическими методами, такими как число обмотки , либо доказательством, сочетающим теорию Галуа и тот факт, что любой действительный многочлен нечетной степени имеет хотя бы один действительный корень.

По этой причине теоремы, справедливые для любого алгебраически замкнутого поля, применимы, например, к любой непустой комплексной квадратной матрице , которая имеет по крайней мере одно (комплексное) собственное значение . ${\displaystyle \mathbb {C} .}$

Алгебраическая характеристика

Поле имеет следующие три свойства: ${\displaystyle \mathbb {C} }$

• Во-первых, он имеет характеристику 0. Это означает, что 1 + 1 + ⋯ + 1 ≠ 0 для любого количества слагаемых (все из которых равны единице).
• Во-вторых, степень его трансцендентности над основным полем — это мощность континуума . ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {C} ,}$
• В-третьих, оно алгебраически замкнуто (см. выше).

Можно показать, что любое поле, обладающее этими свойствами, изоморфно (как поле). Например, алгебраическое замыкание поля p - адического числа также удовлетворяет этим трем свойствам, поэтому эти два поля изоморфны (как поля, но не как топологические поля). ^[53] Кроме того, изоморфно полю комплексных рядов Пюизо . Однако для определения изоморфизма требуется аксиома выбора . Другим следствием этой алгебраической характеристики является то, что она содержит множество собственных подполей, изоморфных . ${\displaystyle \mathbb {C} .}$ ${\displaystyle \mathbb {Q} _{p}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

Характеризация как топологическое поле

Предыдущая характеристика описывает только алгебраические аспекты. То есть свойства близости и непрерывности , которые важны в таких областях, как анализ и топология , не рассматриваются. Следующее описание топологического поля (то есть поля, снабженного топологией , допускающей понятие сходимости) не учитывает топологические свойства. содержит подмножество P (а именно набор положительных действительных чисел) ненулевых элементов, удовлетворяющих следующим трем условиям: ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} .}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

• P замкнут при сложении, умножении и обратном.
• Если x и y — различные элементы P , то либо x − y , либо y − x находится в P.
• Если S — любое непустое подмножество P , то S + P = x + P для некоторого x из ${\displaystyle \mathbb {C} .}$

Более того, имеет нетривиальный инволютивный автоморфизм x ↦ x * (а именно комплексное сопряжение), такой что x x * находится в P для любого ненулевого x в ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} .}$

Любое поле F с этими свойствами можно наделить топологией, взяв множества B ( x ,  p ) = {  y | p − ( y − x )( y − x )* ∈ P  }  в качестве базы , где x пробегает поле, а p пробегает P . В этой топологии F изоморфно как топологическое поле ${\displaystyle \mathbb {C} .}$

Единственными связными локально компактными топологическими полями являются и Это дает еще одну характеристику поля как топологического поля, поскольку его можно отличить от того, что ненулевые комплексные числа связаны , а ненулевые действительные числа - нет. ^[54] ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} .}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} }$

Формальная конструкция

Конструкция в виде упорядоченных пар

Уильям Роуэн Гамильтон представил подход к определению набора комплексных чисел ^[55] как набора упорядоченных пар ( a ,  b ) действительных чисел, в котором налагаются следующие правила сложения и умножения: ^[51] ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} ^{2}}$

$${\displaystyle {\begin{aligned}(a,b)+(c,d)&=(a+c,b+d)\\(a,b)\cdot (c,d)&=(ac-bd,bc+ad).\end{aligned}}}$$

Тогда это просто вопрос обозначения, чтобы выразить ( a ,  b ) как a + bi .

Строительство как факторполе

Хотя эта низкоуровневая конструкция действительно точно описывает структуру комплексных чисел, следующее эквивалентное определение более непосредственно раскрывает алгебраическую природу числа. Эта характеристика опирается на понятие полей и полиномов. Поле — это набор, наделенный операциями сложения, вычитания, умножения и деления, которые ведут себя так же, как, скажем, из рациональных чисел. Например, распределительный закон ${\displaystyle \mathbb {C} }$

$${\displaystyle (x+y)z=xz+yz}$$

xyzp ( X )коэффициентами ${\displaystyle \mathbb {R} }$

$${\displaystyle a_{n}X^{n}+\dotsb +a_{1}X+a_{0},}$$

a ₀ , ...,  a _nструктурукольцом полиномов ${\displaystyle \mathbb {R} [X]}$

Набор комплексных чисел определяется как факторкольцо ^[6]. Это поле расширения содержит два квадратных корня из −1 , а именно ( смежные классы ) X и − X соответственно. (Смежные классы) 1 и X образуют основу реального векторного пространства , что означает, что каждый элемент поля расширения может быть однозначно записан как линейная комбинация этих двух элементов. Эквивалентно, элементы поля расширения могут быть записаны как упорядоченные пары ( a ,  b ) действительных чисел. Факторкольцо является полем, поскольку X ² + 1 неприводимо , поэтому порождаемый им идеал максимален . ${\displaystyle \mathbb {R} [X]/(X^{2}+1).}$ ${\displaystyle \mathbb {R} [X]/(X^{2}+1)}$ ${\displaystyle \mathbb {R} ,}$

Формулы сложения и умножения в кольце по модулю отношения X ² = −1 соответствуют формулам сложения и умножения комплексных чисел, определенных как упорядоченные пары. Таким образом , два определения поля изоморфны (как поля). ${\displaystyle \mathbb {R} [X],}$ ${\displaystyle \mathbb {C} }$

Следовательно, принятие того, что это алгебраически замкнуто, поскольку оно является алгебраическим расширением в этом подходе, является алгебраическим замыканием ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} .}$

Матричное представление комплексных чисел

Комплексные числа a + bi также можно представить матрицами размера 2 × 2 , имеющими вид

$${\displaystyle {\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}.}$$

abкольца2 × 2

Простое вычисление показывает, что карта

$${\displaystyle a+ib\mapsto {\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}}$$

кольцевым изоморфизмомопределителемматрицы

Геометрическое описание умножения комплексных чисел также можно выразить через матрицы вращения , используя это соответствие между комплексными числами и такими матрицами. Действие матрицы на вектор ( x , y ) соответствует умножению x + iy на a + ib . В частности, если определитель равен 1 , существует действительное число t такое, что матрица имеет вид

$${\displaystyle {\begin{pmatrix}\cos t&-\sin t\\\sin t&\;\;\cos t\end{pmatrix}}.}$$

поворотомt ${\displaystyle \cos t+i\sin t}$

Комплексный анализ

График цветового круга sin (1/ z ) . Белые части внутри относятся к числам, имеющим большие абсолютные значения.

Изучение функций комплексной переменной известно как комплексный анализ и имеет огромное практическое применение как в прикладной математике , так и в других разделах математики. Часто наиболее естественные доказательства утверждений реального анализа или даже теории чисел используют методы комплексного анализа ( пример см. в теореме о простых числах ). В отличие от реальных функций, которые обычно представляются в виде двумерных графиков, сложные функции имеют четырехмерные графики и могут быть с пользой проиллюстрированы путем цветового кодирования трехмерного графика, чтобы обозначить четыре измерения, или путем анимации динамического преобразования сложной функции. сложный самолет.

Сложные экспоненциальные и родственные функции

Понятия сходящегося ряда и непрерывных функций в (реальном) анализе имеют естественные аналоги в комплексном анализе. Говорят, что последовательность комплексных чисел сходится тогда и только тогда, когда сходятся ее действительная и мнимая части. Это эквивалентно (ε, δ)-определению пределов , где абсолютное значение действительных чисел заменяется абсолютным значением комплексных чисел. С более абстрактной точки зрения, , наделенная метрикой ${\displaystyle \mathbb {C} }$

$${\displaystyle \operatorname {d} (z_{1},z_{2})=|z_{1}-z_{2}|}$$

метрическим пространствомнеравенство треугольника

$${\displaystyle |z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|}$$

z ₁z ₂

Как и в реальном анализе, это понятие сходимости используется для построения ряда элементарных функций : показательная функция exp z , также обозначаемая e ^z , определяется как бесконечный ряд

$${\displaystyle \exp z:=1+z+{\frac {z^{2}}{2\cdot 1}}+{\frac {z^{3}}{3\cdot 2\cdot 1}}+\cdots =\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}.}$$

Ряд, определяющий действительные тригонометрические функции sin и cosine , а также гиперболические функции sinh и cosh, также переносится без изменения на комплексные аргументы. С другими тригонометрическими и гиперболическими функциями, такими как tangent , дела обстоят несколько сложнее, поскольку определяющие ряды сходятся не для всех комплексных значений. Поэтому их необходимо определять либо через синус, косинус и экспоненту, либо, что то же самое, используя метод аналитического продолжения .

Формула Эйлера гласит:

$${\displaystyle \exp(i\varphi )=\cos \varphi +i\sin \varphi }$$

φ

$${\displaystyle \exp(i\pi )=-1}$$

тождеством Эйлерабесконечное числоz

$${\displaystyle \exp z=w}$$

w ≠ 0zкомплексным логарифмом,

$${\displaystyle \log w=\ln |w|+i\arg w,}$$

аргумент,натуральный логарифммногозначная функция2 πзначение( − π , π ]

Комплексное возведение в степень z ^ω определяется как

$${\displaystyle z^{\omega }=\exp(\omega \ln z),}$$

ωω = 1/ nnn

Комплексные числа, в отличие от действительных чисел, в целом не удовлетворяют тождествам неизмененной степени и логарифма, особенно если их наивно рассматривать как однозначные функции; см. отказ степени и логарифмического тождества . Например, они не удовлетворяют

$${\displaystyle a^{bc}=\left(a^{b}\right)^{c}.}$$

Голоморфные функции

Функция f : → называется голоморфной в точке, если она комплексно дифференцируема в открытой окрестности этой точки. Необходимым (но не достаточным) условием голоморфности f является то, что она удовлетворяет уравнениям Коши–Римана . Например, любое -линейное отображение → можно записать в виде ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

$${\displaystyle f(z)=az+b{\overline {z}}}$$

abтогда и только тогда, когда b = 0уравнениям Коши–Римана ${\displaystyle {\overline {z}}}$

Комплексный анализ показывает некоторые особенности, не очевидные при реальном анализе. Например, любые две голоморфные функции f и g , которые согласуются на сколь угодно малом открытом подмножестве , обязательно согласуются везде. Мероморфные функции , функции, которые локально могут быть записаны как f ( z )/( z - z ₀ ) ⁿ с голоморфной функцией f , по-прежнему имеют некоторые общие черты голоморфных функций. Другие функции имеют существенные особенности , такие как sin(1/ z ) при z = 0 . ${\displaystyle \mathbb {C} }$

Приложения

Комплексные числа находят применение во многих научных областях, включая обработку сигналов , теорию управления , электромагнетизм , гидродинамику , квантовую механику , картографию и анализ вибрации . Некоторые из этих приложений описаны ниже.

Геометрия

Формы

Три неколлинеарные точки на плоскости определяют форму треугольника . Располагая точки на комплексной плоскости, эту форму треугольника можно выразить комплексной арифметикой как ${\displaystyle u,v,w}$ ${\displaystyle \{u,v,w\}}$

$${\displaystyle S(u,v,w)={\frac {u-w}{u-v}}.}$$

аффинного преобразованиясходствоклассу подобия^[56] ${\displaystyle S}$ ${\displaystyle \{u,v,w\}}$

Фрактальная геометрия

Набор Мандельброта с помеченными действительными и мнимыми осями.

Множество Мандельброта — популярный пример фрактала, образованного на комплексной плоскости. Он определяется путем нанесения на график каждого места , где итерация последовательности не расходится при бесконечной итерации . Аналогично, множества Джулии имеют те же правила, за исключением того, что они остаются постоянными. ${\displaystyle c}$ ${\displaystyle f_{c}(z)=z^{2}+c}$ ${\displaystyle c}$

Треугольники

Каждый треугольник имеет уникальный эллипс Штейнера – эллипс внутри треугольника, касающийся середин трех сторон треугольника. Фокусы эллипса Штейнера треугольника можно найти следующим образом, согласно теореме Мардена : ^{[57] [58]} Обозначим вершины треугольника в комплексной плоскости как a = x _A + y _A i , b = x _B + y _B i , и c знак равно Икс _C + y _C я . Напишите кубическое уравнение , возьмите его производную и приравняйте (квадратную) производную нулю. Теорема Мардена гласит, что решениями этого уравнения являются комплексные числа, обозначающие положения двух фокусов эллипса Штейнера. ${\displaystyle (x-a)(x-b)(x-c)=0}$

Алгебраическая теория чисел

Построение правильного пятиугольника с помощью линейки и циркуля .

Как уже говорилось выше, любое непостоянное полиномиальное уравнение (с комплексными коэффициентами) имеет решение в . Тем более то же самое верно, если уравнение имеет рациональные коэффициенты. Корни таких уравнений называются алгебраическими числами — они являются основным объектом изучения в теории алгебраических чисел . По сравнению с , алгебраическое замыкание , которое также содержит все алгебраические числа, имеет то преимущество, что его легко понять в геометрических терминах. Таким образом, алгебраические методы можно использовать для изучения геометрических вопросов и наоборот. С помощью алгебраических методов, более конкретно применяя аппарат теории поля к числовому полю , содержащему корни из единицы , можно показать, что невозможно построить правильный девятиугольник , используя только циркуль и линейку - чисто геометрическая проблема. ${\displaystyle \mathbb {C} }$ ${\displaystyle {\overline {\mathbb {Q} }}}$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {C} }$

Другой пример — целые числа Гаусса ; то есть числа вида x + iy , где x и y — целые числа, которые можно использовать для классификации сумм квадратов .

Аналитическая теория чисел

Аналитическая теория чисел изучает числа, часто целые или рациональные числа, используя тот факт, что их можно рассматривать как комплексные числа, для которых можно использовать аналитические методы. Это делается путем кодирования теоретико-числовой информации в комплексных функциях. Например, дзета-функция Римана ζ( s ) связана с распределением простых чисел .

Несобственные интегралы

В прикладных областях комплексные числа часто используются для вычисления некоторых действительных несобственных интегралов с помощью комплексных функций. Для этого существует несколько методов; см. методы контурного интегрирования .

Динамические уравнения

В дифференциальных уравнениях обычно сначала находят все комплексные корни r характеристического уравнения линейного дифференциального уравнения или системы уравнений, а затем пытаются решить систему в терминах базовых функций вида f ( t ) = e ^rt . Аналогично, в разностных уравнениях используются комплексные корни r характеристического уравнения системы разностных уравнений, чтобы попытаться решить систему с точки зрения базовых функций формы f ( t ) = r ^t .

Линейная алгебра

Собственное разложение — полезный инструмент для вычисления степеней матриц и экспонент . Однако часто требуется использование комплексных чисел, даже если матрица действительная (например, матрица вращения ).

Комплексные числа часто обобщают концепции, изначально заложенные в вещественных числах. Например, сопряженное транспонирование обобщает транспонирование , эрмитовы матрицы обобщают симметричные матрицы , а унитарные матрицы обобщают ортогональные матрицы .

В прикладной математике

Теория управления

В теории управления системы часто преобразуются из временной области в комплексную частотную область с использованием преобразования Лапласа . Затем нули и полюса системы анализируются в комплексной плоскости . Методы корневого годографа , графика Найквиста и графика Николса используют комплексную плоскость.

В методе корневого годографа важно, находятся ли нули и полюса в левой или правой полуплоскостях, то есть имеют действительную часть больше или меньше нуля. Если линейная, нестационарная (LTI) система имеет полюсы, которые

• в правой полуплоскости он будет неустойчив ,
• все в левой полуплоскости, будет устойчиво ,
• на мнимой оси он будет иметь предельную устойчивость .

Если система имеет нули в правой полуплоскости, это неминимально-фазовая система.

Анализ сигналов

Комплексные числа используются в анализе сигналов и других областях для удобного описания периодически меняющихся сигналов. Для данных действительных функций, представляющих реальные физические величины, часто в терминах синусов и косинусов, рассматриваются соответствующие комплексные функции, действительные части которых являются исходными величинами. Для синусоидального сигнала заданной частоты абсолютное значение | г | соответствующего z является амплитудой , а аргумент arg z является фазой .

Если анализ Фурье используется для записи данного действительного сигнала в виде суммы периодических функций, эти периодические функции часто записываются как комплексные функции вида

$${\displaystyle x(t)=\operatorname {Re} \{X(t)\}}$$

и

$${\displaystyle X(t)=Ae^{i\omega t}=ae^{i\phi }e^{i\omega t}=ae^{i(\omega t+\phi )}}$$

где ω представляет угловую частоту , а комплексное число A кодирует фазу и амплитуду, как объяснено выше.

Это использование также распространяется на цифровую обработку сигналов и цифровую обработку изображений , которые используют цифровые версии анализа Фурье (и вейвлет- анализа) для передачи, сжатия , восстановления и иной обработки цифровых аудиосигналов , неподвижных изображений и видеосигналов .

Другой пример, относящийся к двум боковым полосам амплитудной модуляции AM-радио:

$${\displaystyle {\begin{aligned}\cos((\omega +\alpha )t)+\cos \left((\omega -\alpha )t\right)&=\operatorname {Re} \left(e^{i(\omega +\alpha )t}+e^{i(\omega -\alpha )t}\right)\\&=\operatorname {Re} \left(\left(e^{i\alpha t}+e^{-i\alpha t}\right)\cdot e^{i\omega t}\right)\\&=\operatorname {Re} \left(2\cos(\alpha t)\cdot e^{i\omega t}\right)\\&=2\cos(\alpha t)\cdot \operatorname {Re} \left(e^{i\omega t}\right)\\&=2\cos(\alpha t)\cdot \cos \left(\omega t\right).\end{aligned}}}$$

По физике

Электромагнетизм и электротехника

В электротехнике преобразование Фурье используется для анализа изменяющихся напряжений и токов . Тогда подход к резисторам , конденсаторам и катушкам индуктивности можно унифицировать, введя для последних двух мнимые, зависящие от частоты сопротивления и объединив все три в одно комплексное число, называемое импедансом . Этот подход называется векторным исчислением.

В электротехнике мнимая единица обозначается j , чтобы избежать путаницы с I , которая обычно используется для обозначения электрического тока , или, более конкретно, i , которая обычно используется для обозначения мгновенного электрического тока.

Поскольку напряжение в цепи переменного тока является колебательным, его можно представить как

$${\displaystyle V(t)=V_{0}e^{j\omega t}=V_{0}\left(\cos \omega t+j\sin \omega t\right),}$$

Для получения измеримой величины берут действительную часть:

$${\displaystyle v(t)=\operatorname {Re} (V)=\operatorname {Re} \left[V_{0}e^{j\omega t}\right]=V_{0}\cos \omega t.}$$

Комплексный сигнал V ( t ) называется аналитическим представлением действительного измеримого сигнала v ( t ) .^[59]

Динамика жидкостей

В гидродинамике сложные функции используются для описания потенциального потока в двух измерениях .

Квантовая механика

Поле комплексных чисел присуще математическим формулировкам квантовой механики , где комплексные гильбертовы пространства обеспечивают контекст для одной такой формулировки, которая является удобной и, возможно, наиболее стандартной. Исходные основные формулы квантовой механики – уравнение Шрёдингера и матричная механика Гейзенберга – используют комплексные числа.

относительность

В специальной и общей теории относительности некоторые формулы для метрики пространства-времени становятся проще, если считать временную составляющую пространственно-временного континуума мнимой. (Этот подход больше не является стандартным в классической теории относительности, но существенно используется в квантовой теории поля .) Комплексные числа необходимы для спиноров , которые являются обобщением тензоров, используемых в теории относительности.

Обобщения и родственные понятия

Граф кватернионов Кэли Q8, показывающий циклы умножения на i , j и k

Процесс расширения поля действительных чисел известен как конструкция Кэли-Диксона . Его можно перенести и на более высокие измерения, получив кватернионы и октонионы , которые (как реальное векторное пространство) имеют размерность 4 и 8 соответственно. В этом контексте комплексные числа были названы бинарионами . ^[60] ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {O} }$

Подобно тому, как при применении конструкции к действительным числам теряется свойство упорядоченности , свойства, знакомые действительным и комплексным числам, исчезают с каждым расширением. Кватернионы теряют коммутативность, то есть x · y ≠ y · x для некоторых кватернионов x ,  y , а умножение октонионов , помимо того, что оно не является коммутативным, не может быть ассоциативным: ( x · y )· z ≠ x ·( y · z ) для некоторых октонионов x ,  y ,  z .

Вещественные числа, комплексные числа, кватернионы и октонионы — все это нормированные алгебры с делением над . По теореме Гурвица они единственные; седенионы , следующий шаг в конструкции Кэли- Диксона , не имеют такой структуры. ${\displaystyle \mathbb {R} }$

Конструкция Кэли-Диксона тесно связана с регулярным представлением мысли как -алгебры ( -векторного пространства с умножением) относительно базиса (1,  i ) . Это означает следующее: -линейное отображение ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$

$${\displaystyle {\begin{aligned}\mathbb {C} &\rightarrow \mathbb {C} \\z&\mapsto wz\end{aligned}}}$$

w2 × 2(1,  i )

$${\displaystyle {\begin{pmatrix}\operatorname {Re} (w)&-\operatorname {Im} (w)\\\operatorname {Im} (w)&\operatorname {Re} (w)\end{pmatrix}},}$$

линейное представление ${\displaystyle \mathbb {C} }$

$${\displaystyle J={\begin{pmatrix}p&q\\r&-p\end{pmatrix}},\quad p^{2}+qr+1=0}$$

J ² = − I

$${\displaystyle \{z=aI+bJ:a,b\in \mathbb {R} \}}$$

линейной комплексной структуры ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {R} ^{2}.}$

Гиперкомплексные числа также обобщают и. Например, это понятие содержит расщепленные комплексные числа , которые являются элементами кольца (в отличие от комплексных чисел). В этом кольце уравнение a ² = 1 имеет четыре решения. ${\displaystyle \mathbb {R} ,}$ ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {H} ,}$ ${\displaystyle \mathbb {O} .}$ ${\displaystyle \mathbb {R} [x]/(x^{2}-1)}$ ${\displaystyle \mathbb {R} [x]/(x^{2}+1)}$

Поле является пополнением поля рациональных чисел относительно обычной метрики абсолютного значения . Другие варианты метрик на приводят к полям p -адических чисел ( для любого простого числа p ), которые тем самым аналогичны . Других нетривиальных способов пополнения, кроме и по теореме Островского, не существует . Алгебраические замыкания еще несут в себе норму, но (в отличие от ) не полны относительно нее. Пополнение оказывается алгебраически замкнутым. По аналогии это поле называется p -адическими комплексными числами. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} ,}$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {Q} _{p}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} _{p},}$ ${\displaystyle {\overline {\mathbb {Q} _{p}}}}$ ${\displaystyle \mathbb {Q} _{p}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} _{p}}$ ${\displaystyle {\overline {\mathbb {Q} _{p}}}}$

Поля и их конечные расширения полей, в том числе, называются локальными полями . ${\displaystyle \mathbb {R} ,}$ ${\displaystyle \mathbb {Q} _{p},}$ ${\displaystyle \mathbb {C} ,}$

Смотрите также

• Алгебраическая поверхность
• Круговое движение с использованием комплексных чисел
• Комплексно-базовая система
• Сложная геометрия
• Двойное комплексное число
• целое число Эйзенштейна
• Геометрическая алгебра (которая включает комплексную плоскость как двумерное спинорное подпространство ) ${\displaystyle {\mathcal {G}}_{2}^{+}}$
• Комплексный номер единицы

Примечания

1. «Комплексные числа, так же, как и действительные числа, а, возможно, даже больше, обретают поистине удивительное единство с природой. Как будто сама Природа впечатлена масштабом и последовательностью системы комплексных чисел так же, как и мы сами, и доверила этим числам точное управление своим миром в мельчайших масштабах». - Р. Пенроуз (2016, стр. 73) ^[2]
2. Соломенцев 2001: «Плоскость , точки которой отождествляются с элементами, называется комплексной плоскостью... Полная геометрическая интерпретация комплексных чисел и операций над ними появилась впервые в работе К. Весселя (1799). Геометрическое представление Комплексных чисел, иногда называемая «диаграммой Аргана», вошла в употребление после публикации в 1806 и 1814 годах статей Дж. Р. Аргана, который заново открыл, в основном независимо, открытия Весселя». ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {C} }$
3. В литературе мнимая единица часто предшествует радикальному знаку, даже если ей предшествует целое число. ^[21]
4. Пьером Лораном Ванцелем в 1843 году, Винченцо Молламе в 1890 году, Отто Гёльдером в 1891 году и Адольфом Кнезером в 1892 году было доказано, что мнимые числа обязательно появляются в кубической формуле, когда уравнение имеет три действительных разных корня. Паоло Руффини также доказал неполное доказательство в 1799 г. —— С. Конфалоньери (2015) ^[23]
5. Арганд 1814, с. 204 определяет модуль комплексного числа, но не дает ему названия:
   «Dans ce quisuit, les Accens, Indifféremment Places, Seront Employés pour indiquer la grandeur absolue des qu’ils effectent; ainsi, si , et étant réels, on devra entender que ou ». ${\displaystyle a=m+n{\sqrt {-1}}}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle a_{'}}$ ${\displaystyle a'={\sqrt {m^{2}+n^{2}}}}$
   [В дальнейшем знаки ударения, где бы они ни располагались, будут использоваться для обозначения абсолютного размера величин, которым они присвоены; таким образом , если и будучи реальным, следует понимать это или .] Argand 1814, p. 208 определяет и называет модуль и фактор направления комплексного числа: «...  pourrait être appelé le Module de , et représenterait la grandeur absolue de la ligne , tandis que l'autre facteur, dont le Module est l'unité, и являюсь представителем направления». [...  можно было бы назвать модулем и представлять абсолютный размер линии (Арган представлял комплексные числа в виде векторов.), тогда как другой фактор [а именно, ], модуль которого равен единице [1], представлял бы ее направление. ] ${\displaystyle a=m+n{\sqrt {-1}}}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle a_{'}}$ ${\displaystyle a'={\sqrt {m^{2}+n^{2}}}}$
   ${\displaystyle a={\sqrt {m^{2}+n^{2}}}}$ ${\displaystyle a+b{\sqrt {-1}}}$ ${\displaystyle a+b{\sqrt {-1}}}$
   ${\displaystyle a={\sqrt {m^{2}+n^{2}}}}$ ${\displaystyle a+b{\sqrt {-1}}}$ ${\displaystyle a+b{\sqrt {-1}}\,,}$ ${\displaystyle {\tfrac {a}{\sqrt {a^{2}+b^{2}}}}+{\tfrac {b}{\sqrt {a^{2}+b^{2}}}}{\sqrt {-1}}}$
6. Гаусс пишет: ^[43] «Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter Solos numeros integros reales versatur, ita теорема около остатка биквадратики tunc tantum in summa simplicitate ac genuina venustate блистательная, quando campus arithmeticae ad quantitates imaginarias простирается itur, ita ut absquestricte ipsius obiectum, составляющее числа formae a + bi , denotantibus i , pro more quantitatem imaginariam , atque ${\displaystyle {\sqrt {-1}}}$ a, b indefinite omnes numeros reales integros inter - et + ». ${\displaystyle \infty }$ ${\displaystyle \infty }$[Конечно, точно так же, как высшая арифметика до сих пор исследовалась в задачах только с действительными целыми числами, так и теоремы о биквадратных вычетах тогда сияют величайшей простотой и подлинной красотой, когда область арифметики расширяется до мнимых величин, так что без ограничения на него, числа вида a + bi — i , обозначающие по соглашению мнимую величину , и переменные a, b [обозначающие] все действительные целые числа между и — составляют объект.] ${\displaystyle {\sqrt {-1}}}$ ${\displaystyle -\infty }$ ${\displaystyle +\infty }$
7. Гаусс: ^[44] «Tales numeros vocabimus numeros integros complexos, ita quidem, ut Reales complexis non opponantur, sed tamquam specs sub his contineri censeantur». [Мы будем называть такие числа [а именно, числа вида a + bi ] «комплексными целыми числами», так что действительные [числа] рассматриваются не как противоположность комплексным [числам], а [как] тип [числа, который ] как бы содержится в них.]
8. Гаусс: ^[45] «Productum numeri complexi per numerum ipsi conjunctum utriusquenormalam vocamus . Pro Norma itaque numeri realis, ipsiusquadratum habendum est». [Мы называем «нормой» произведение комплексного числа [например, a + ib ] на сопряженное ему [ a - ib ]. Поэтому квадрат действительного числа следует считать его нормой.]
9. Однако для другой обратной функции комплексной экспоненциальной функции (а не определенного выше главного значения) разрез ветки может быть сделан на любом другом луче , проходящем через начало координат.

Рекомендации

1. Подробное описание истории «мнимых» чисел, от первоначального скептицизма до окончательного принятия, см. в Bourbaki, Nicolas (1998). «Основы математики § Логика: теория множеств». Элементы истории математики . Спрингер. стр. 18–24.
2. Пенроуз, Роджер (2016). Дорога к реальности: полное руководство по законам Вселенной (переиздание). Случайный дом. стр. 72–73. ISBN 978-1-4464-1820-8.
3. Экслер, Шелдон (2010). Колледж алгебры . Уайли. п. 262. ИСБН 9780470470770.
4. Шпигель, MR; Липшуц, С.; Шиллер, Джей-Джей; Спеллман, Д. (14 апреля 2009 г.). Комплексные переменные . Серия набросков Шаума (2-е изд.). МакГроу Хилл. ISBN 978-0-07-161569-3.
5. Ауфманн, Ричард Н.; Баркер, Вернон К.; Нация, Ричард Д. (2007). «Глава П». Колледж алгебры и тригонометрии (6-е изд.). Cengage Обучение. п. 66. ИСБН 978-0-618-82515-8.
6. Бурбаки 1998, §VIII.1
7. Альфорс 1979.
8. Кэмпбелл, Джордж Эшли (апрель 1911 г.). «Цисоидальные колебания» (PDF) . Труды Американского института инженеров-электриков . Американский институт инженеров-электриков . XXX (1–6): 789–824 [рис. 13 на стр. 810]. дои : 10.1109/PAIEE.1911.6659711. S2CID  51647814 . Проверено 24 июня 2023 г. п. 789: Использование i (или греческого ı ) для воображаемого символа почти универсально в математической работе, что является очень веской причиной для сохранения его в приложениях математики в электротехнике. Однако, помимо установленных соглашений и возможности ссылки на математическую литературу, замена символа j вызывает возражения из-за векторной терминологии, с которой он стал ассоциироваться в технической литературе, а также из-за путаницы, возникающей из-за разделенная практика писателей-инженеров: некоторые используют j вместо + i , а другие используют j вместо - i .
9. Браун, Джеймс Уорд; Черчилль, Руэл В. (1996). Комплексные переменные и приложения (6-е изд.). Нью-Йорк, США: МакГроу-Хилл . п. 2. ISBN 978-0-07-912147-9. п. 2: В электротехнике вместо i используется буква j .
10. Педо, Дэн (1988). Геометрия: Комплексный курс . Дувр. ISBN 978-0-486-65812-4.
11. Вайсштейн, Эрик В. «Комплексное число». mathworld.wolfram.com . Проверено 12 августа 2020 г.
12. Апостол 1981, с. 18.
13. Касана, HS (2005). "Глава 1". Комплексные переменные: теория и приложения (2-е изд.). PHI Learning Pvt. ООО с. 14. ISBN 978-81-203-2641-5.
14. Нильссон, Джеймс Уильям; Ридель, Сьюзен А. (2008). «Глава 9». Электрические цепи (8-е изд.). Прентис Холл. п. 338. ИСБН 978-0-13-198925-2.
15. Клайн, Моррис. История математической мысли, том 1 . п. 253.
16. Юрий, Кович. Тристан Нидэм, Визуальный комплексный анализ, Oxford University Press Inc., Нью-Йорк, 1998, 592 страницы. ОСЛК  1080410598.
17. О'Коннор и Робертсон (2016), «Джироламо Кардано».
18. Нахин, Пол Дж. Воображаемая сказка: История √−1. Принстон: Издательство Принстонского университета, 1998.
19. Кац, Виктор Дж. (2004). «9.1.4». История математики, краткая версия . Аддисон-Уэсли . ISBN 978-0-321-16193-2.
20. Гамильтон, Wm. (1844 г.). «О новом виде мнимых величин, связанном с теорией кватернионов». Труды Королевской ирландской академии . 2 : 424–434.
21. Синтия Ю. Янг (2017). Тригонометрия (4-е изд.). Джон Уайли и сыновья. п. 406. ИСБН 978-1-119-44520-3.Выдержка из страницы 406
22. Нахин, Пол Дж. (2007). Воображаемая сказка: История √−1. Издательство Принстонского университета . ISBN 978-0-691-12798-9. Архивировано из оригинала 12 октября 2012 года . Проверено 20 апреля 2011 г.
23. Конфалоньери, Сара (2015). Недостижимая попытка избежать Casus Irreducibilis для кубических уравнений: De Regula Aliza Джероламо Кардано . Спрингер. стр. 15–16 (прим. 26). ISBN 978-3658092757.
24. Декарт, Рене (1954) [1637]. Ла Геометрия | Геометрия Рене Декарта с факсимиле первого издания. Дуврские публикации . ISBN 978-0-486-60068-0. Проверено 20 апреля 2011 г.
25. Эйлер, Леонард (1748). Introductio in Analysin Infinitorum [ Введение в анализ бесконечного ] (на латыни). Том. 1. Люцерн, Швейцария: Marc Michel Bosquet & Co., с. 104.
26. Вессель, Каспар (1799). «Om Directionens analytiske Betegning, et Forsog, anvendt fornemmelig til plane og sphæriske Polygoners Oplosning» [Об аналитическом представлении направления, попытка, приложенная, в частности, к определению плоских и сферических многоугольников]. Nye Samling af det Kongelige Danske Videnskabernes Selskabs Skrifter [Новое собрание сочинений Датского королевского научного общества] (на датском языке). 5 : 469–518.
27. Уоллис, Джон (1685). Трактат по алгебре, как исторический, так и практический ... Лондон, Англия: напечатано Джоном Плейфордом для Ричарда Дэвиса. стр. 264–273.
28. Арганд (1806). Essai sur une manière de représenter les quantités imaginaires dans les builds géométriques [ Эссе о способе представления комплексных величин с помощью геометрических конструкций ] (на французском языке). Париж, Франция: Мадам Вев Блан.
29. Гаусс, Карл Фридрих (1799) «Demonstratio nova теорематис omnem functionem алгебраический рационалем интеграм униус вариалис в факторах реальных первоначальных и секундных градусах разрешения». [Новое доказательство теоремы о том, что любая рациональная целая алгебраическая функция одной переменной может быть разложена на действительные множители первой или второй степени.] Доктор философии. диссертация, Университет Хельмштедта (Германия). (на латыни)
30. Эвальд, Уильям Б. (1996). От Канта до Гильберта: Справочник по основам математики. Том. 1. Издательство Оксфордского университета. п. 313. ИСБН 9780198505358. Проверено 18 марта 2020 г.
31. Гаусс 1831, с. 638.
32. "Адриан Квентин Буэ (1745–1845): МакТьютор".
33. Буэ (1806). «Mémoire sur les quantités imaginaires» [Мемуары о мнимых количествах]. Философские труды Лондонского королевского общества (на французском языке). 96 : 23–88. дои : 10.1098/rstl.1806.0003. S2CID  110394048.
34. Мури, CV (1861). La vraies théore des quantités négatives et des quantités pétendues imaginaires [ Истинная теория отрицательных величин и предполагаемых мнимых величин ] (на французском языке). Париж, Франция: Малле-Башелье. Репринт 1861 года с оригинала 1828 года.
35. Уоррен, Джон (1828). Трактат о геометрическом представлении квадратных корней из отрицательных величин. Кембридж, Англия: Издательство Кембриджского университета.
36. Уоррен, Джон (1829). «Рассмотрение возражений, выдвинутых против геометрического представления квадратных корней из отрицательных величин». Философские труды Лондонского королевского общества . 119 : 241–254. дои : 10.1098/rstl.1829.0022 . S2CID  186211638.
37. Уоррен, Джон (1829). «О геометрическом представлении степеней величин, индексы которых включают квадратные корни отрицательных чисел». Философские труды Лондонского королевского общества . 119 : 339–359. дои : 10.1098/rstl.1829.0031 . S2CID  125699726.
38. Франсэ, JF (1813). «Новые принципы геометрии положения и геометрическая интерпретация сложных [числовых] символов». Annales des mathématiques pures et appliquées (на французском языке). 4 : 61–71.
39. Капаррини, Сандро (2000). «Об общем происхождении некоторых работ по геометрической интерпретации комплексных чисел». В Ким Уильямс (ред.). Две культуры. Биркхойзер. п. 139. ИСБН 978-3-7643-7186-9.
40. Харди, GH; Райт, Э.М. (2000) [1938]. Введение в теорию чисел . ОУП Оксфорд . п. 189 (четвертое издание). ISBN 978-0-19-921986-5.
41. Джефф Миллер (21 сентября 1999 г.). «МОДУЛЬ». Самые ранние известные варианты использования некоторых математических слов (M) . Архивировано из оригинала 3 октября 1999 года.{{cite web}}: CS1 maint: unfit URL (link)
42. Коши, Огюстен-Луи (1821). Курс анализа королевской политехнической школы (на французском языке). Том. 1. Париж, Франция: L'Imprimerie Royale. п. 183.
43. Гаусс 1831, с. 96
44. Гаусс 1831, с. 96
45. Гаусс 1831, с. 98
46. Ханкель, Герман (1867). Vorlesungen über die complexen Zahlen und ihre Functionen [ Лекции о комплексных числах и их функциях ] (на немецком языке). Том. 1. Лейпциг, [Германия]: Леопольд Восс. п. 71. Из стр. 71: «Wir werden den Factor ( cos φ + i sin φ) haüfig den Richtungscoefficienten nennen». (Мы часто будем называть фактор (cos φ + i sin φ) «коэффициентом направления».)
47. Первые обозначения см. в Apostol 1981, стр. 15–16.
48. Абрамовиц, Милтон; Стегун, Ирен А. (1964). Справочник математических функций с формулами, графиками и математическими таблицами. Публикации Courier Dover. п. 17. ISBN 978-0-486-61272-0. Архивировано из оригинала 23 апреля 2016 года . Проверено 16 февраля 2016 г., раздел 3.7.26, с. 17. Архивировано 10 сентября 2009 г. в Wayback Machine.
49. Кук, Роджер (2008). Классическая алгебра: ее природа, происхождение и использование. Джон Уайли и сыновья. п. 59. ИСБН 978-0-470-25952-8. Архивировано из оригинала 24 апреля 2016 года . Проверено 16 февраля 2016 г., Извлечение: стр. 59. Архивировано 23 апреля 2016 г. в Wayback Machine.
50. Альфорс 1979, с. 3.
51. Апостол 1981, стр. 15–16.
52. Апостол 1981, с. 25.
53. Маркер, Дэвид (1996). «Введение в модельную теорию полей». В Маркере, Д.; Мессмер, М.; Пиллэй, А. (ред.). Модельная теория полей . Конспект лекций по логике. Том. 5. Берлин: Шпрингер-Верлаг. стр. 1–37. ISBN 978-3-540-60741-0. МР  1477154.
54. Бурбаки 1998, §VIII.4.
55. Корри, Лео (2015). Краткая история чисел . Издательство Оксфордского университета. стр. 215–16.
56. Лестер, Дж. А. (1994). «Треугольники I: Формы». Математические уравнения . 52 : 30–54. дои : 10.1007/BF01818325. S2CID  121095307.
57. Кальман, Дэн (2008a). «Элементарное доказательство теоремы Мардена». Американский математический ежемесячник . 115 (4): 330–38. дои : 10.1080/00029890.2008.11920532. ISSN  0002-9890. S2CID  13222698. Архивировано из оригинала 8 марта 2012 года . Проверено 1 января 2012 г.
58. Кальман, Дэн (2008b). «Самая чудесная теорема математики». Журнал онлайн-математики и ее приложений . Архивировано из оригинала 8 февраля 2012 года . Проверено 1 января 2012 г.
59. Грант, И.С.; Филлипс, WR (2008). Электромагнетизм (2-е изд.). Манчестерская серия по физике. ISBN 978-0-471-92712-9.
60. МакКриммон, Кевин (2004). Вкус жордановой алгебры . Университеттекст. Спрингер. п. 64. ИСБН 0-387-95447-3. МР 2014924

Цитируемые работы

• Альфорс, Ларс (1979). Комплексный анализ (3-е изд.). МакГроу-Хилл. ISBN 978-0-07-000657-7.
• Апостол, Том (1981). Математический анализ . Аддисон-Уэсли.
• Арган (1814 г.). «Размышления о новой теории комплексных чисел с последующим применением к доказательству теоремы анализа». Annales de mathématiques pures et appliquées (на французском языке). 5 : 197–209.
• Гаусс, CF (1831). «Theoria residuorum biquadraticorum. Commentatio secunda» [Теория биквадратичных остатков. Второе воспоминание.]. Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores (на латыни). 7 : 89–148.
• Соломенцев, Е.Д. (2001) [1994], «Комплексное число», Энциклопедия Математики , EMS Press

дальнейшее чтение

• Пенроуз, Роджер (2005). Дорога к реальности: Полное руководство по законам Вселенной. Альфред А. Кнопф. ISBN 978-0-679-45443-4.
• Дербишир, Джон (2006). Неизвестное количество: реальная и воображаемая история алгебры. Джозеф Генри Пресс. ISBN 978-0-309-09657-7.
• Нидхэм, Тристан (1997). Визуальный комплексный анализ . Кларендон Пресс. ISBN 978-0-19-853447-1.

Математический

• Альфорс, Ларс (1979). Комплексный анализ (3-е изд.). МакГроу-Хилл. ISBN 978-0-07-000657-7.
• Конвей, Джон Б. (1986). Функции одной комплексной переменной I . Спрингер. ISBN 978-0-387-90328-6.
• Джоши, Капил Д. (1989). Основы дискретной математики . Нью-Йорк: Джон Уайли и сыновья . ISBN 978-0-470-21152-6.
• Педо, Дэн (1988). Геометрия: Комплексный курс . Дувр. ISBN 978-0-486-65812-4.
• Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007). «Раздел 5.5 Комплексная арифметика». Численные рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-88068-8. Архивировано из оригинала 13 марта 2020 года . Проверено 9 августа 2011 г.
• Соломенцев, Е.Д. (2001) [1994], «Комплексное число», Энциклопедия Математики , EMS Press

Исторический

• Бурбаки, Николя (1998). «Основы математики § логика: теория множеств». Элементы истории математики . Спрингер.
• Бертон, Дэвид М. (1995). История математики (3-е изд.). Нью-Йорк: МакГроу-Хилл . ISBN 978-0-07-009465-9.
• Кац, Виктор Дж. (2004). История математики, краткая версия . Аддисон-Уэсли . ISBN 978-0-321-16193-2.
• Нахин, Пол Дж. (1998). Воображаемая сказка: История ${\displaystyle \scriptstyle {\sqrt {-1}}}$ . Издательство Принстонского университета. ISBN 978-0-691-02795-1.— Небольшое введение в историю комплексных чисел и начало комплексного анализа.
• Эббингауз, HD; Гермес, Х.; Хирцебрух, Ф.; Кочер, М.; Майнцер, К.; Нойкирх, Дж.; Престель, А.; Реммерт, Р. (1991). Числа (изд. в твердом переплете). Спрингер. ISBN 978-0-387-97497-2.— Передовой взгляд на историческое развитие понятия числа.