
В теории музыки интервал — это разница в высоте тона между двумя звуками. [1] Интервал можно описать как горизонтальный , линейный или мелодический , если он относится к последовательно звучащим тонам, например, двум соседним тонам в мелодии, и вертикальный или гармонический, если он относится к одновременно звучащим тонам, например, в аккорде . [2] [3]
В западной музыке интервалы чаще всего представляют собой различия между нотами диатонической гаммы . Интервалы между последовательными нотами гаммы также известны как шаги гаммы. Наименьший из этих интервалов — полутон . Интервалы меньше полутона называются микротонами . Они могут быть образованы с использованием нот различных видов недиатонических гамм. Некоторые из самых маленьких называются запятыми и описывают небольшие расхождения, наблюдаемые в некоторых системах настройки , между энгармонически эквивалентными нотами, такими как C ♯ и D ♭ . Интервалы могут быть произвольно малыми и даже незаметными для человеческого уха.
В физическом смысле интервал — это соотношение между двумя звуковыми частотами. Например, любые две ноты, отстоящие друг от друга на октаву, имеют соотношение частот 2:1. Это означает, что последовательные увеличения высоты тона на один и тот же интервал приводят к экспоненциальному увеличению частоты, хотя человеческое ухо воспринимает это как линейное увеличение высоты тона. По этой причине интервалы часто измеряются в центах — единице, полученной из логарифма соотношения частот.
В западной музыкальной теории наиболее распространенная схема наименования интервалов описывает два свойства интервала: качество (совершенный, мажор, минор, увеличенный, уменьшенный) и число (унисон, секунда, терция и т. д.). Примерами являются малая терция или совершенная квинта . Эти названия определяют не только разницу в полутонах между верхними и нижними нотами, но и то, как пишется интервал . Важность написания вытекает из исторической практики дифференциации частотных соотношений энгармонических интервалов, таких как G–G ♯ и G–A ♭ . [4]

Размер интервала (также известный как его ширина или высота) можно представить с помощью двух альтернативных и одинаково допустимых методов, каждый из которых подходит для определенного контекста: частотных отношений или центов.
Размер интервала между двумя нотами может быть измерен отношением их частот . Когда музыкальный инструмент настроен с использованием системы настройки только интонации , размер основных интервалов может быть выражен малыми целыми отношениями, такими как 1:1 ( унисон ), 2:1 ( октава ), 5:3 ( большая секста ), 3:2 ( чистая квинта ), 4:3 ( чистая кварта ), 5:4 ( большая терция ), 6:5 ( малая терция ). Интервалы с малыми целыми отношениями часто называют просто интервалами или чистыми интервалами .
Однако чаще всего музыкальные инструменты в настоящее время настраиваются с использованием другой системы настройки, называемой 12-тоновой равномерной темперацией . Как следствие, размер большинства равномерно темперированных интервалов не может быть выражен малыми целыми отношениями, хотя он очень близок к размеру соответствующих точных интервалов. Например, равномерно темперированная квинта имеет соотношение частот 2 7 ⁄ 12 : 1, что приблизительно равно 1,498: 1 или 2,997: 2 (очень близко к 3: 2). Для сравнения размера интервалов в различных системах настройки см. § Размер интервалов, используемых в различных системах настройки.
Стандартная система для сравнения размеров интервалов — с центами . Цент — логарифмическая единица измерения. Если частота выражена в логарифмической шкале , и по этой шкале расстояние между заданной частотой и ее удвоенной (также называемой октавой ) разделено на 1200 равных частей, каждая из этих частей составляет один цент. В двенадцатитонной равномерной темперации (12-TET), системе настройки, в которой все полутоны имеют одинаковый размер, размер одного полутона составляет ровно 100 центов. Следовательно, в 12-TET цент также может быть определен как одна сотая полутона .
Математически размер интервала от частоты f 1 до частоты f 2 в центах равен
В таблице приведены наиболее широко используемые общепринятые названия интервалов между нотами хроматической гаммы . Совершенный унисон (также известный как совершенный штрих) [5] — это интервал, образованный двумя одинаковыми нотами. Его размер — ноль центов . Полутон — это любой интервал между двумя соседними нотами в хроматической гамме, целый тон — это интервал, охватывающий два полутона (например, большая секунда ), а тритон — это интервал, охватывающий три тона или шесть полутонов (например, увеличенная кварта). [a] Редко термин дитон также используется для обозначения интервала, охватывающего два целых тона (например, большая терция ), или, более строго, как синоним большой терции.
Интервалы с разными названиями могут охватывать одинаковое количество полутонов и даже иметь одинаковую ширину. Например, интервал от D до F ♯ является большой терцией , а от D до G ♭ — уменьшенной квартой . Однако оба они охватывают 4 полутона. Если инструмент настроен так, что 12 нот хроматической гаммы расположены одинаково (как в равномерно темперированном строе ), эти интервалы также имеют одинаковую ширину. А именно, все полутоны имеют ширину 100 центов , а все интервалы, охватывающие 4 полутона, имеют ширину 400 центов.
Перечисленные здесь названия не могут быть определены только путем подсчета полутонов. Правила их определения объясняются ниже. Другие названия, определенные с помощью других соглашений об именовании, перечислены в отдельном разделе. Интервалы меньше одного полутона (запятые или микротоны) и больше одной октавы (составные интервалы) представлены ниже.

В западной музыкальной теории интервал называется в соответствии с его номером (также называемым диатоническим номером, размером интервала [6] или общим интервалом [7] ) и качеством . Например, большая терция (или M3 ) — это название интервала, в котором термин большая ( M ) описывает качество интервала, а терция ( 3 ) указывает на его номер.


Номер интервала — это количество буквенных названий или позиций нотного стана (линий и пробелов), которые он охватывает, включая позиции обеих нот, образующих интервал. Например, интервал B—D является терцией (обозначается m3 ), потому что ноты от B до D над ним охватывают три буквенных названия (B, C, D) и занимают три последовательные позиции нотного стана, включая позиции B и D. Таблица и рисунок выше показывают интервалы с номерами от 1 (например, P1 ) до 8 (например, d8 ). Интервалы с большими номерами называются составными интервалами.
Существует однозначное соответствие между позициями нотного стана и ступенями диатонической гаммы (нотами диатонической гаммы ). [b] Это означает, что номера интервалов также можно определить, подсчитав ступени диатонической гаммы, а не позиции нотного стана, при условии, что две ноты, которые образуют интервал, взяты из диатонической гаммы. А именно, B—D является терцией, потому что в любой диатонической гамме, содержащей B и D, последовательность от B до D включает три ноты. Например, в диатонической гамме B- натуральный минор три ноты — это B–C ♯ –D. Это не относится ко всем видам гамм. Например, в хроматической гамме есть четыре ноты от B до D: B–C–C ♯ –D. Вот почему номера интервалов также называются диатоническими числами , и эта договоренность называется диатонической нумерацией .
Если к нотам, образующим интервал, добавить знаки альтерации , по определению, ноты не изменят своего положения на стане. Как следствие, любой интервал имеет тот же номер интервала, что и соответствующий натуральный интервал, образованный теми же нотами без знаков альтерации. Например, интервалы B–D ♯ (охватывающие 4 полутона) и B–D ♭ (охватывающие 2 полутона) являются терциями, как и соответствующий натуральный интервал B—D (3 полутона).
Обратите внимание, что номера интервалов представляют собой включающее количество охватываемых позиций нот или названий нот, а не разницу между конечными точками. Другими словами, отсчет нижней тональности начинается с единицы, а не с нуля. По этой причине интервал E–E, совершенный унисон, также называется примой (что означает «1»), хотя между конечными точками нет разницы. Продолжая, интервал E–F ♯ является секундой, но F ♯ является только одной позицией нот или ступенью диатонической гаммы выше E. Аналогично, E—G ♯ является терцией, но G ♯ является только двумя позициями нот выше E и так далее. Как следствие, объединение двух интервалов всегда дает номер интервала на единицу меньше их суммы. Например, интервалы B—D и D—F ♯ являются терциями, но, соединенные вместе, они образуют квинту (B—F ♯ ), а не сексту. Аналогично, стопка из трех терций, например B—D, D—F ♯ и F ♯ —A, является септаккордом (BA), а не нонаккордом.
Эта схема применима к интервалам до октавы (12 полутонов). Для более длинных интервалов см. § Составные интервалы ниже.
Название любого интервала дополнительно уточняется с использованием терминов совершенный ( P ), мажорный ( M ), минорный ( m ), увеличенный ( A ) и уменьшенный ( d ). Это называется его качеством интервала (или модификатором [8] [7] ). Возможно иметь дважды уменьшенные и дважды увеличенные интервалы, но они довольно редки, так как встречаются только в хроматических контекстах. Сочетание числа (или общего интервала) и качества (или модификатора) называется специфическим интервалом [7] диатоническим интервалом (иногда используется только для интервалов, появляющихся в диатонической гамме) или просто интервалом [8 ]
Качество составного интервала — это качество простого интервала, на котором он основан. Некоторые другие определители, такие как neutral , subminor и supermajor , используются для недиатонических интервалов.

Совершенные интервалы так называются, потому что они традиционно считались совершенно консонансными, [9] хотя в западной классической музыке совершенная кварта иногда рассматривалась как несовершенный консонанс, когда ее функция была контрапунктической . [ неопределенно ] Наоборот, малые, большие, увеличенные или уменьшенные интервалы обычно считаются менее консонансными и традиционно классифицировались как посредственные консонансы, несовершенные консонансы или почти диссонансы. [9]
В диатонической гамме [b] все унисоны ( P1 ) и октавы ( P8 ) являются совершенными. Большинство кварт и квинт также являются совершенными ( P4 и P5 ), с пятью и семью полутонами соответственно. Одно появление кварты является увеличенной ( A4 ), а одна квинта — уменьшенной ( d5 ), оба охватывают шесть полутонов. Например, в ми-мажорной гамме A4 находится между A и D ♯ , а d5 — между D ♯ и A.
Обращение совершенного интервала также совершенно. Поскольку обращение не меняет класс высоты тона двух нот, оно почти не влияет на их уровень консонанса (соответствие их гармоник ). Наоборот, другие виды интервалов имеют противоположное качество по отношению к их обращению. Обращение большого интервала — это малый интервал, обращение увеличенного интервала — это уменьшенный интервал.

Как показано в таблице, диатоническая гамма [b] определяет семь интервалов для каждого номера интервала, каждый из которых начинается с другой ноты (семь унисон, семь секунд и т. д.). Интервалы, образованные нотами диатонической гаммы, называются диатоническими. За исключением унисон и октав, диатонические интервалы с заданным номером интервала всегда встречаются в двух размерах, которые отличаются на один полутон. Например, шесть квинт охватывают семь полутонов. Другая охватывает шесть полутонов. Четыре терции охватывают три полутона, остальные четыре. Если одна из двух версий является совершенным интервалом, другая называется либо уменьшенной (т. е. суженной на один полутон), либо увеличенной (т. е. расширенной на один полутон). В противном случае большая версия называется мажорной, меньшая — минорной. Например, поскольку квинта в 7 полутонов является совершенным интервалом ( P5 ), квинта в 6 полутонов называется «уменьшенной квинтой» ( d5 ). И наоборот, поскольку ни один из видов терции не является совершенным, больший из них называется «большой терцией» ( M3 ), меньший — «малой терцией» ( m3 ).
В диатонической гамме [b] унисоны и октавы всегда квалифицируются как чистые, кварты — как чистые или увеличенные, квинты — как чистые или уменьшенные, а все остальные интервалы (секунды, терции, сексты, септимы) — как большие или малые.

Увеличенные интервалы шире на один полутон, чем чистые или большие интервалы, при этом имея то же самое число интервалов (т. е. охватывая то же самое число позиций нотного стана): они шире на хроматический полутон . Уменьшенные интервалы, с другой стороны, уже на один полутон, чем чистые или малые интервалы того же числа интервалов: они уже на хроматический полутон. Например, увеличенная секста, такая как E ♭ –C ♯, охватывает десять полутонов, превышая большую сексту (E ♭ —C) на один полутон, в то время как уменьшенная секста, такая как E ♯ –C, охватывает семь полутонов, отставая от малой сексты (E ♯ –C ♯ ) на один полутон.
Увеличенная кварта ( A4 ) и уменьшенная квинта ( d5 ) являются единственными увеличенными и уменьшенными интервалами, которые появляются в диатонических гаммах [b] (см. таблицу).
Ни количество, ни качество интервала не могут быть определены только подсчетом полутонов . Как объяснялось выше, необходимо также учитывать количество позиций нотного стана.
Например, как показано в таблице ниже, существует шесть полутонов между C и F ♯ , C и G ♭ , и C ♭ и E ♯ , но
Интервалы часто сокращаются с помощью P для совершенного, m для минорного , M для мажорного , d для уменьшенного , A для увеличенного , за которыми следует номер интервала. Обозначения M и P часто опускаются. Октава — P8, а унисон обычно называют просто «унисоном», но его можно обозначить P1. Тритон , увеличенная кварта или уменьшенная квинта часто обозначают TT . Качества интервалов также могут сокращаться с помощью perf , min , maj , dim , aug . Примеры:

Простой интервал (т. е. интервал, меньший или равный октаве) можно инвертировать , повышая нижнюю ноту на октаву или понижая верхнюю ноту на октаву. Например, кварту от более низкой C до более высокой F можно инвертировать, чтобы получить квинту, от более низкой F до более высокой C.
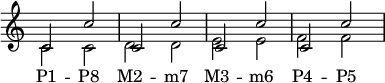
Существует два правила для определения количества и качества инверсии любого простого интервала: [10]
Например, интервал от C до E ♭ над ним — это малая терция. Согласно двум только что данным правилам, интервал от E ♭ до C над ним должен быть большой секстой.
Поскольку составные интервалы больше октавы, «обращение любого составного интервала всегда такое же, как обращение простого интервала, из которого он составлен» [11] .
Для интервалов, идентифицированных по их отношению, инверсия определяется путем обращения отношения и умножения отношения на 2 до тех пор, пока оно не станет больше 1. Например, инверсия отношения 5:4 — это отношение 8:5.
Для интервалов, определяемых целым числом полутонов, инверсия получается путем вычитания этого числа из 12.
Поскольку класс интервала представляет собой наименьшее число, выбранное среди целого числа интервала и его инверсии, классы интервала не могут быть инвертированы.
Интервалы можно описывать, классифицировать или сравнивать друг с другом по различным критериям.

Интервал можно описать как
В общем,
Таблица выше отображает 56 диатонических интервалов, образованных нотами гаммы C мажор (диатоническая гамма). Обратите внимание, что эти интервалы, как и любой другой диатонический интервал, могут быть образованы также нотами хроматической гаммы.
Различие между диатоническими и хроматическими интервалами является спорным, поскольку оно основано на определении диатонической гаммы, которое варьируется в литературе. Например, интервал B–E ♭ ( уменьшенная кварта , встречающаяся в гармонической гамме C-minor ) считается диатоническим, если гармонические минорные гаммы также считаются диатоническими. [12] В противном случае он считается хроматическим. Более подробную информацию см. в основной статье .
Согласно общепринятому определению диатонической гаммы [b] (исключающему гармоническую минорную и мелодическую минорную гаммы), все совершенные, мажорные и минорные интервалы являются диатоническими. Наоборот, ни один увеличенный или уменьшенный интервал не является диатоническим, за исключением увеличенной кварты и уменьшенной квинты.

Различие между диатоническими и хроматическими интервалами также может быть чувствительным к контексту. Вышеупомянутые 56 интервалов, образованных гаммой C-major, иногда называются диатоническими до C-major . Все остальные интервалы называются хроматическими до C-major . Например, чистая квинта A ♭ –E ♭ является хроматической до C-major, потому что A ♭ и E ♭ не содержатся в гамме C-major. Однако она является диатонической по отношению к другим, таким как гамма A ♭ major.
Консонанс и диссонанс — это относительные термины, которые относятся к стабильности или состоянию покоя определенных музыкальных эффектов. Диссонансные интервалы — это те, которые вызывают напряжение и желание разрешиться в консонансные интервалы.
Эти термины относятся к использованию различных композиционных стилей.
Все вышеприведенные анализы относятся к вертикальным (одновременным) интервалам.

Простой интервал — это интервал, охватывающий не более одной октавы (см. Основные интервалы выше). Интервалы, охватывающие более одной октавы, называются составными интервалами, поскольку их можно получить, добавив одну или несколько октав к простому интервалу (см. подробности ниже). [20]
Линейные (мелодические) интервалы можно описать как шаги или пропуски . Шаг , или конъюнктивное движение , [21] — это линейный интервал между двумя последовательными нотами гаммы. Любой больший интервал называется пропуском ( также называется скачком ) или дизъюнктивным движением . [21] В диатонической гамме [b] шаг — это либо малая секунда (иногда также называемая полушагом ), либо большая секунда (иногда также называемая целым шагом ), при этом все интервалы малой терции или больше являются пропусками.
Например, нота C — D (большая секунда) — это шаг, а нота C — E ( большая терция ) — это скачок.
В более общем смысле, шаг — это меньший или узкий интервал в музыкальной строке, а скачок — это более широкий или больший интервал, где разделение интервалов на шаги и скачки определяется системой настройки и используемым диапазоном высоты тона .
Мелодическое движение , в котором интервал между любыми двумя последовательными тонами не превышает одного шага или, менее строго, где скачки редки, называется пошаговым или связным мелодическим движением, в отличие от скачков или разъединенных мелодических движений, характеризующихся частыми скачками.

Два интервала считаются энгармоническими или энгармонически эквивалентными , если они оба содержат одни и те же высоты, записанные по-разному; то есть, если ноты в двух интервалах сами по себе энгармонически эквивалентны. Энгармонические интервалы охватывают одинаковое количество полутонов .
Например, четыре интервала, перечисленные в таблице ниже, все энгармонически эквивалентны, поскольку ноты F ♯ и G ♭ указывают на одинаковую высоту тона, и то же самое верно для A ♯ и B ♭ . Все эти интервалы охватывают четыре полутона.
При игре в качестве изолированных аккордов на клавиатуре пианино эти интервалы неразличимы на слух, поскольку все они играются с помощью одних и тех же двух клавиш. Однако в музыкальном контексте диатоническая функция нот, которые включают эти интервалы, сильно отличается.
Приведенное выше обсуждение предполагает использование распространенной системы настройки, 12-тоновой равномерной темперации («12-TET»). Но в других исторических темперациях meanone высоты пар нот, таких как F ♯ и G ♭, могут не обязательно совпадать. Эти две ноты являются энгармоническими в 12-TET, но могут не быть таковыми в другой системе настройки. В таких случаях интервалы, которые они образуют, также не будут энгармоническими. Например, в meanone quarter-comma все четыре интервала, показанные в примере выше, будут разными.

Существует также ряд минутных интервалов, не встречающихся в хроматической гамме или помеченных диатонической функцией, которые имеют собственные названия. Их можно описать как микротоны , а некоторые из них можно также классифицировать как коммы , поскольку они описывают небольшие расхождения, наблюдаемые в некоторых системах настройки, между энгармонически эквивалентными нотами. В следующем списке размеры интервалов в центах являются приблизительными.

Составной интервал — это интервал, охватывающий более одной октавы. [20] И наоборот, интервалы, охватывающие не более одной октавы, называются простыми интервалами (см. Основные интервалы ниже).
В общем, составной интервал может быть определен последовательностью или «стопкой» двух или более простых интервалов любого вида. Например, большая десятка (две нотные позиции выше одной октавы), также называемая составной большой терцией , охватывает одну октаву плюс одну большую терцию.
Любой составной интервал всегда можно разложить на одну или несколько октав плюс один простой интервал. Например, большую септаккорду можно разложить на две октавы и одну большую терцию, и именно поэтому она называется составной большой терцией, даже если она построена путем сложения четырех квинт.
Диатоническое число DN c сложного интервала, образованного из n простых интервалов с диатоническими числами DN 1 , DN 2 , ..., DN n , определяется по формуле:
что также можно записать как:
Качество составного интервала определяется качеством простого интервала, на котором он основан. Например, составная большая терция — это большая децима (1+(8−1)+(3−1) = 10) или большая семнадцатая (1+(8−1)+(8−1)+(3−1) = 17), а составная чистая квинта — это чистая двенадцатая (1+(8−1)+(5−1) = 12) или чистая девятнадцатая (1+(8−1)+(8−1)+(5−1) = 19). Обратите внимание, что две октавы — это пятнадцатая, а не шестнадцатая (1+(8−1)+(8−1) = 15). Аналогично, три октавы составляют двадцать вторую (1+3×(8−1) = 22), четыре октавы составляют двадцать девятую (1+3×(8-1) = 29) и т. д.
Здесь также стоит упомянуть большую семнадцатую (28 полутонов) — интервал больше двух октав, который можно считать кратным чистой квинте (7 полутонов), поскольку его можно разложить на четыре чистые квинты (7 × 4 = 28 полутонов) или две октавы плюс большая терция (12 + 12 + 4 = 28 полутонов). Интервалы больше большой семнадцатой встречаются редко, чаще всего их называют составными названиями, например, «две октавы плюс квинта» [22], а не «девятнадцатая».
Аккорды — это наборы из трех или более нот. Обычно они определяются как комбинация интервалов, начинающихся с общей ноты, называемой тоникой аккорда . Например, мажорное трезвучие — это аккорд, содержащий три ноты, определяемые тоником, и два интервала (большая терция и чистая квинта). Иногда даже один интервал ( диада ) считается аккордом. [23] Аккорды классифицируются на основе качества и количества интервалов, которые их определяют.
Основные качества аккорда — мажор , минор , увеличенный , уменьшенный , полууменьшенный и доминант . Символы, используемые для качества аккорда, аналогичны тем, которые используются для интервального качества (см. выше). Кроме того, + или aug используется для увеличенного, ° или dim для уменьшенного, ø для полууменьшенного и dom для доминанты (символ − сам по себе не используется для уменьшенного).
Основные правила расшифровки названий аккордов или символов приведены ниже. Более подробная информация приведена в Правилах расшифровки названий аккордов и символов .
Таблица показывает интервалы, содержащиеся в некоторых основных аккордах ( компонентные интервалы ), и некоторые символы, используемые для их обозначения. Качества интервалов или числа, выделенные жирным шрифтом, можно вывести из названия аккорда или символа, применив правило 1. В примерах символов C используется как основной тон аккорда.
В этой таблице сравниваются ширины интервалов, используемые в четырех различных системах настройки. Для облегчения сравнения жирным шрифтом показаны только интервалы , предоставляемые настройкой с 5 пределами (см. симметричную шкалу № 1 ) , а значения в центах округлены до целых чисел. Обратите внимание, что в каждой из неравных систем настройки по определению ширина каждого типа интервала (включая полутон) изменяется в зависимости от ноты, с которой начинается интервал. Это искусство правильной интонации . В равномерной темперации интервалы никогда не бывают точно настроены друг на друга. Это цена использования равноудаленных интервалов в 12-тоновой шкале. Для простоты для некоторых типов интервалов в таблице показано только одно значение ( наиболее часто наблюдаемое ).
В 1 ⁄ 4 -comma meanone , по определению, 11 чистых квинт имеют размер приблизительно 697 центов (700 − ε центов, где ε ≈ 3,42 цента); поскольку средний размер 12 квинт должен быть равен ровно 700 центам (как в равномерно темперированном строе), то другая должна иметь размер приблизительно 738 центов (700 + 11 ε , волчья квинта или уменьшенная секста ); 8 больших терций имеют размер приблизительно 386 центов (400 − 4 ε ), 4 имеют размер приблизительно 427 центов (400 + 8 ε , на самом деле уменьшенные кварты ), а их средний размер составляет 400 центов. Короче говоря, схожие различия в ширине наблюдаются для всех типов интервалов, за исключением унисон и октав, и все они кратны ε (разнице между 1 ⁄ 4 -comma meanone и средней квинтой). Более подробный анализ представлен в 1 ⁄ 4 -comma meanone Размер интервалов . 1 ⁄ 4 -comma meanone был разработан для создания только больших терций, но только 8 из них являются именно такими (5:4, около 386 центов).
Пифагорейский строй характеризуется меньшими различиями, поскольку они кратны меньшему ε ( ε ≈ 1,96 цента, разница между пифагорейской квинтой и средней квинтой). Обратите внимание, что здесь квинта шире 700 центов, в то время как в большинстве темпераций мезонина , включая 1 ⁄ 4 -комма мезонина, она темперирована до размера меньше 700. Более подробный анализ представлен в Пифагорейский строй § Размер интервалов .
Система настройки 5-limit использует только тоны и полутоны в качестве строительных блоков, а не стек чистых квинт, и это приводит к еще большему разнообразию интервалов по всей гамме (каждый вид интервала имеет три или четыре разных размера). Более подробный анализ представлен в разделе Настройка 5-limit § Размер интервалов . Настройка 5-limit была разработана для максимизации количества только интервалов, но даже в этой системе некоторые интервалы не являются только интервалами (например, 3 квинты, 5 больших терций и 6 малых терций не являются только интервалами; также 3 больших и 3 малых терции являются интервалами вольфа ).
Вышеупомянутая симметричная гамма 1, определенная в системе настройки 5-limit, не является единственным методом получения just intonation . Можно построить juster интервалы или just intervals, более близкие к равномерно темперированным эквивалентам, но большинство из перечисленных выше использовались исторически в эквивалентных контекстах. В частности, асимметричная версия шкалы настройки 5-limit обеспечивает juster значение для малой септимы (9:5, а не 16:9). Более того, тритон (увеличенная кварта или уменьшенная квинта) может иметь другие just соотношения; например, 7:5 (около 583 центов) или 17:12 (около 603 центов) являются возможными альтернативами для увеличенной кварты (последний довольно распространен, так как он ближе к равномерно темперированному значению 600 центов). Интервал 7:4 (около 969 центов), также известный как гармонический септим , был спорным вопросом на протяжении всей истории теории музыки; это на 31 цент ниже, чем равномерно темперированная минорная септаккорда. Для получения дополнительной информации о справочных соотношениях см. 5-предельная настройка § Самые справедливые соотношения .
В диатонической системе каждый интервал имеет один или несколько энгармонических эквивалентов , например, увеличенная секунда для малой терции .

Хотя интервалы обычно обозначаются относительно их нижней ноты, Дэвид Коуп [19] и Хиндемит [24] оба предлагают концепцию корня интервала . Чтобы определить корень интервала, нужно найти его ближайшее приближение в гармоническом ряду. Корень чистой кварты, таким образом, является его верхней нотой, поскольку это октава основной тональности в гипотетическом гармоническом ряду. Нижняя нота каждого нечетного диатонически пронумерованного интервала является корнем, как и верхние ноты всех четных интервалов. Таким образом, корень набора интервалов или аккорда определяется корнем интервала его самого сильного интервала.
Что касается его полезности, Коуп [19] приводит пример финального тонического аккорда некоторой популярной музыки, который традиционно анализируется как «субмедиантный секстаккорд» ( добавленные секстаккорды по популярной терминологии) или первый инверсионный септаккорд (возможно, доминанта медианта V/iii). Согласно основному тону самого сильного интервала аккорда (в первом обращении, CEGA), чистая квинта (C–G) — это нижняя C, тоника.
Интервальные циклы , «разворачивают [т. е. повторяют] один повторяющийся интервал в серии, которая закрывается возвратом к начальному классу высоты тона», и обозначаются Джорджем Перлом с использованием буквы «C» для цикла, с целым числом класса интервала для различения интервала. Таким образом, уменьшенный септаккорд будет C3, а увеличенное трезвучие будет C4. Можно добавить верхний индекс для различения транспозиций, используя 0–11 для указания самого низкого класса высоты тона в цикле. [25]
Как показано ниже, некоторые из вышеупомянутых интервалов имеют альтернативные названия, а некоторые из них принимают особое альтернативное название в пифагорейской настройке , настройке с пятью пределами или системах настройки с темперацией типа « четверть-комма» meanone . Все интервалы с префиксом sesqui- настроены справедливо , а их отношение частот , показанное в таблице, является суперчастным числом (или эпиморическим отношением). То же самое верно и для октавы.
Обычно запятая — это уменьшенная секунда, но это не всегда так (более подробную информацию см. в разделе Альтернативные определения запятой ). Например, в пифагорейском строе уменьшенная секунда — это нисходящий интервал (524288:531441 или около −23,5 центов), а пифагорейская запятая — ее противоположность (531441:524288 или около 23,5 центов). Настройка с 5-пределом определяет четыре вида запятой , три из которых соответствуют определению уменьшенной секунды и, следовательно, перечислены в таблице ниже. Четвертая, называемая синтонической запятой (81:80), не может рассматриваться ни как уменьшенная секунда, ни как ее противоположность. Более подробную информацию см. в разделе Уменьшенные секунды в настройке с 5-пределом .
Кроме того, некоторые культуры по всему миру имеют свои собственные названия для интервалов, встречающихся в их музыке. Например, 22 вида интервалов, называемых шрути , канонически определены в индийской классической музыке .
До конца XVIII века латынь использовалась в качестве официального языка по всей Европе для научных и музыкальных учебников. В музыке многие английские термины произошли от латыни. Например, полутон происходит от латинского semitonus .
Префикс semi- обычно используется здесь для обозначения «короче», а не «половина». [26] [27] [28] А именно, semitonus, semiditonus, semidiatessaron, semidiapente, semihexachordum, semiheptachordum или semidiapason короче на один полутон, чем соответствующий целый интервал. Например, semiditonus (3 полутона или около 300 центов) — это не половина ditonus (4 полутона или около 400 центов), а ditonus, сокращенный на один полутон. Более того, в пифагорейской настройке (наиболее часто используемая система настройки вплоть до XVI века) semitritonus (d5) меньше tritonus (A4) на одну пифагорейскую комму (около четверти полутона).
Интервалы в недиатонических гаммах могут быть названы с использованием аналогов названий диатонических интервалов, используя диатонический интервал похожего размера и различая его, изменяя качество, или добавляя другие модификаторы. Например, точный интервал 7/6 может быть назван субминорной терцией , так как он составляет ~267 центов в ширину, что уже, чем малая терция (300 центов в 12-TET, ~316 центов для точного интервала 6/5), или септимальной малой терцией , так как это интервал с пределом в 7. Эти названия относятся только к размеру отдельного интервала, и номер интервала не обязательно должен соответствовать количеству ступеней гаммы (гептатонической). Такое наименование особенно распространено в точных интонационных и микротональных гаммах. [29]
Наиболее распространенными из этих расширенных качеств являются нейтральный интервал , между малым и большим интервалом; и субминорные и супермажорные интервалы , соответственно уже, чем мажорный или шире, чем мажорный интервал. Точный размер таких интервалов зависит от системы настройки, но они часто отличаются от размеров диатонических интервалов примерно на четверть тона (50 центов, половина хроматического шага). Например, нейтральная секунда , характерный интервал арабской музыки , в 24-TET составляет 150 центов, точно посередине между малой секундой и большой секундой. В совокупности они дают прогрессию уменьшенный, субминорный, минорный, нейтральный, мажорный, супермажорный, увеличенный для секунд, терций, секст и септим. Это соглашение об именовании может быть распространено на унисоны, кварты, квинты и октавы с суб и супер , давая прогрессию уменьшенный, суб, совершенный, супер, увеличенный . Это позволяет называть все интервалы в 24-TET или 31-TET, последний из которых был использован Адрианом Фоккером . Различные дальнейшие расширения используются в ксенгармонической музыке . [29]
В посттональной или атональной теории, изначально разработанной для равномерно темперированной европейской классической музыки, написанной с использованием двенадцатитоновой техники или сериализма , часто используется целочисленная нотация , наиболее заметная в теории музыкальных множеств . В этой системе интервалы именуются в соответствии с количеством полутонов, от 0 до 11, наибольший класс интервалов — 6.
В атональной или музыкальной теории множеств существует множество типов интервалов, первый из которых — упорядоченный интервал высоты тона , расстояние между двумя высотами вверх или вниз. Например, интервал от C вверх до G равен 7, а интервал от G вниз до C равен −7. Можно также измерить расстояние между двумя высотами тона без учета направления с помощью неупорядоченного интервала высоты тона, несколько похожего на интервал тональной теории.
Интервал между классами высоты тона может быть измерен с помощью упорядоченных и неупорядоченных интервалов классов высоты тона. Упорядоченный, также называемый направленным интервалом, может считаться мерой вверх, которая, поскольку мы имеем дело с классами высоты тона, зависит от того, какой шаг выбран в качестве 0. Для неупорядоченных интервалов классов высоты тона см. класс интервалов . [30]
В диатонической теории множеств различают специфические и общие интервалы . Специфические интервалы — это класс интервала или число полутонов между ступенями гаммы или членами коллекции, а общие интервалы — это число ступеней диатонической гаммы (или позиций нотного стана) между нотами коллекции или гаммы.
Обратите внимание, что позиции нотного стана, используемые для определения условного номера интервала (секунда, терция, кварта и т. д.), подсчитываются с учетом позиции нижней ноты интервала, в то время как общие номера интервалов подсчитываются без учета этой позиции. Таким образом, общие номера интервалов на 1 меньше, чем обычные номера интервалов.

Термин «интервал» может быть также обобщен на другие музыкальные элементы, помимо высоты тона. В книге Дэвида Левина « Обобщенные музыкальные интервалы и преобразования» интервал используется как общая мера расстояния между временными точками , тембрами или более абстрактными музыкальными явлениями. [31] [32]
Например, интервал между двумя колокольчатыми звуками, которые не имеют выраженности высоты тона, все еще воспринимается. Когда два тона имеют схожие акустические спектры (наборы парциалов), интервал — это просто расстояние смещения спектра тона вдоль оси частот, поэтому привязка к высотам тона как к опорным точкам не является необходимой. Тот же принцип, естественно, применим к тонам с повышенной высотой тона (с похожими гармоническими спектрами), что означает, что интервалы могут восприниматься «напрямую» без распознавания высоты тона. Это объясняет, в частности, преобладание слуха интервала над слухом абсолютной высоты тона . [33] [34]
Согласно двум подходам, некоторые могут форматировать мажорный септаккорд как CM 7 (общее правило 1: M относится к M3), а другие как C M7 (альтернативный подход: M относится к M7). К счастью, даже C M7 становится совместимым с правилом 1, если его рассматривать как сокращение CM M7 , в котором первая M опущена. Опущенная M является качеством терции и выводится согласно правилу 2 (см. выше), в соответствии с интерпретацией простого символа C, который по тому же правилу обозначает CM.
совершенное согласие