Атомная орбиталь

В квантовой механике атомная орбиталь ( / ˈ ɔːr b ɪ t ə l / ) — это функция, описывающая местоположение и волнообразное поведение электрона в атоме . ^{[1] Эта функция описывает}распределение заряда электрона вокруг ядра атома и может использоваться для вычисления вероятности нахождения электрона в определенной области вокруг ядра. ^[2]

Каждая орбиталь в атоме характеризуется набором значений трех квантовых чисел $n$ , $ℓ$ и $m ℓ$ , которые соответственно соответствуют энергии электрона, его орбитальному угловому моменту и его орбитальному угловому моменту, спроецированному вдоль выбранной оси ( магнитное квантовое число ). Орбитали с четко определенным магнитным квантовым числом, как правило, являются комплексными. Действительные орбитали могут быть образованы как линейные комбинации $m ℓ$ и $-m ℓ$ орбиталей и часто маркируются с использованием связанных гармонических полиномов (например, xy , x ² − y ² ), которые описывают их угловую структуру.

Орбиталь может быть занята максимум двумя электронами, каждый со своей собственной проекцией спина . Простые названия s-орбиталь , p-орбиталь , d-орбиталь и f-орбиталь относятся к орбиталям с квантовым числом углового момента $ℓ$ $= 0, 1, 2$ и $3$ соответственно. Эти названия вместе со значениями n используются для описания электронных конфигураций атомов. Они получены из описания ранними спектроскопистами определенных серий спектроскопических линий щелочных металлов как острых , главных , диффузных и фундаментальных . Орбитали для $ℓ$ $> 3$ продолжаются в алфавитном порядке (g, h, i, k, ...), ^[3] опуская j ^[4]^[5], поскольку некоторые языки не различают буквы «i» и «j». ^[6] $m_{s}$

Атомные орбитали являются основными строительными блоками модели атомной орбитали (или модели электронного облака или волновой механики), современной структуры для визуализации субмикроскопического поведения электронов в веществе. В этой модели электронное облако атома можно рассматривать как построенное (в приближении) в электронной конфигурации, которая является продуктом более простых водородоподобных атомных орбиталей. Повторяющаяся периодичность блоков из 2, 6, 10 и 14 элементов в разделах периодической таблицы возникает естественным образом из общего числа электронов, которые занимают полный набор s-, p-, d- и f-орбиталей соответственно, хотя для более высоких значений квантового числа $n$ , особенно когда атом несет положительный заряд, энергии определенных подоболочек становятся очень похожими и, таким образом, порядок , в котором они, как говорят, заселяются электронами (например, Cr = [Ar]4s ¹ 3d ⁵ и Cr ²⁺ = [Ar]3d ⁴ ), может быть рационализирован лишь несколько произвольно.

Свойства электронов

С развитием квантовой механики и экспериментальными открытиями (такими как двухщелевая дифракция электронов) было обнаружено, что электроны, вращающиеся вокруг ядра, не могут быть полностью описаны как частицы, а должны быть объяснены дуализмом волна-частица . В этом смысле электроны обладают следующими свойствами:

Волнообразные свойства:

Электроны не вращаются вокруг ядра подобно планете, вращающейся вокруг звезды, а существуют в виде стоячих волн . Таким образом, наименьшая возможная энергия, которую может получить электрон, подобна основной частоте волны на струне. Более высокие энергетические состояния подобны гармоникам этой основной частоты.
Электроны никогда не находятся в одной точке, хотя вероятность взаимодействия с электроном в одной точке может быть найдена из волновой функции электрона . Заряд электрона действует так, как будто он размазан в пространстве непрерывным распределением, пропорциональным в любой точке квадрату величины волновой функции электрона.

Свойства частиц:

Число электронов, вращающихся вокруг ядра, может быть только целым числом.
Электроны прыгают между орбиталями, как частицы. Например, если один фотон ударяет по электронам, в результате меняется состояние только одного электрона.
Электроны сохраняют свойства частиц, такие как: каждое волновое состояние имеет тот же электрический заряд, что и его частица-электрон. Каждое волновое состояние имеет один дискретный спин (спин вверх или спин вниз) в зависимости от его суперпозиции .

Таким образом, электроны нельзя описать просто как твердые частицы. Аналогией может служить большая и часто странной формы «атмосфера» (электрон), распределенная вокруг относительно маленькой планеты (ядра). Атомные орбитали точно описывают форму этой «атмосферы» только при наличии одного электрона. Когда добавляется больше электронов, дополнительные электроны стремятся более равномерно заполнить объем пространства вокруг ядра, так что результирующая совокупность («электронное облако» ^[7] ) стремится к в целом сферической зоне вероятности, описывающей местоположение электрона, из-за принципа неопределенности .

Следует помнить, что эти орбитальные «состояния», как описано здесь, являются просто собственными состояниями электрона на его орбите. Фактический электрон существует в суперпозиции состояний, которая подобна взвешенному среднему , но с комплексными числовыми весами. Так, например, электрон может находиться в чистом собственном состоянии (2, 1, 0) или смешанном состоянии ⁠1/2⁠ (2, 1, 0) + ⁠1/2⁠ (2, 1, 1) или даже смешанное состояние ⁠ $я$ 2/5⁠ (2, 1, 0) + ⁠3/5⁠ (2, 1, 1). Для каждого собственного состояния свойство имеет собственное значение . Таким образом, для трех упомянутых состояний значение равно 2, а значение равно 1. Для второго и третьего состояний значение является суперпозицией 0 и 1. Как суперпозиция состояний оно неоднозначно — либо точно 0, либо точно 1 — а не промежуточное или среднее значение, как дробь ⁠ $я$ $n$ $л$ $m_{l}$ 1/2⁠ . Суперпозиция собственных состояний (2, 1, 1) и (3, 2, 1) имела бы неоднозначное и , но определенно была бы 1. Собственные состояния облегчают работу с математикой. Вы можете выбрать другой базис собственных состояний, наложив собственные состояния из любого другого базиса (см. Действительные орбитали ниже). $n$ $л$ $m_{l}$

Формальное квантово-механическое определение

Атомные орбитали могут быть определены более точно на формальном языке квантовой механики . Они являются приближенными решениями уравнения Шредингера для электронов, связанных с атомом электрическим полем ядра атома . В частности, в квантовой механике состояние атома, т. е. собственное состояние атомного гамильтониана , аппроксимируется расширением (см. расширение взаимодействия конфигураций и базисный набор ) в линейные комбинации антисимметризованных произведений ( детерминанты Слейтера ) одноэлектронных функций. Пространственные компоненты этих одноэлектронных функций называются атомными орбиталями. (Когда мы рассматриваем также их спиновую составляющую, мы говорим об атомных спиновых орбиталях .) Состояние на самом деле является функцией координат всех электронов, так что их движение коррелировано, но это часто аппроксимируется этой моделью независимых частиц произведений одноэлектронных волновых функций. ^[8] ( Дисперсионная сила Лондона , например, зависит от корреляций движения электронов.)

В атомной физике атомные спектральные линии соответствуют переходам ( квантовым скачкам ) между квантовыми состояниями атома. Эти состояния обозначаются набором квантовых чисел, суммированных в символе термина и обычно связанных с конкретными электронными конфигурациями, т. е. схемами заполнения атомных орбиталей (например, 1s ² 2s ² 2p ⁶ для основного состояния неона - символ термина: ¹ S ₀ ).

Эта нотация означает, что соответствующие детерминанты Слейтера имеют явно более высокий вес в разложении конфигурационного взаимодействия . Поэтому концепция атомной орбитали является ключевой концепцией для визуализации процесса возбуждения, связанного с данным переходом . Например, для данного перехода можно сказать, что он соответствует возбуждению электрона с занятой орбитали на данную незанятую орбиталь. Тем не менее, следует иметь в виду, что электроны являются фермионами, управляемыми принципом исключения Паули , и их невозможно отличить друг от друга. ^[9] Более того, иногда случается, что разложение конфигурационного взаимодействия сходится очень медленно, и вообще нельзя говорить о простой однодетерминантной волновой функции. Это имеет место, когда электронная корреляция велика.

По сути, атомная орбиталь — это одноэлектронная волновая функция, хотя многие электроны не находятся в одноэлектронных атомах, и поэтому одноэлектронное представление является приближением. Когда мы думаем об орбиталях, нам часто дают визуализацию орбитали, на которую сильное влияние оказало приближение Хартри-Фока , что является одним из способов уменьшить сложность теории молекулярных орбиталей .

Типы орбитальных

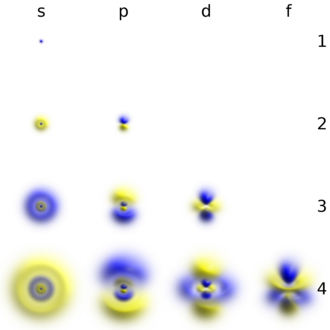
Атомные орбитали могут быть водородоподобными «орбиталями», которые являются точными решениями уравнения Шредингера для водородоподобного «атома» (т. е. атома с одним электроном). В качестве альтернативы атомные орбитали относятся к функциям, которые зависят от координат одного электрона (т. е. орбиталей), но используются в качестве отправных точек для аппроксимации волновых функций, которые зависят от одновременных координат всех электронов в атоме или молекуле. Системы координат , выбранные для орбиталей, обычно являются сферическими координатами $(r, θ, φ)$ в атомах и декартовыми $(x, y, z)$ в многоатомных молекулах. Преимущество сферических координат здесь заключается в том, что орбитальная волновая функция является произведением трех факторов, каждый из которых зависит от одной координаты: $ψ (r, θ, φ) = R (r) Θ(θ) Φ(φ)$ . Угловые факторы атомных орбиталей $Θ(θ) Φ(φ)$ генерируют функции s, p, d и т. д. как действительные комбинации сферических гармоник $Y ℓm (θ, φ)$ (где $ℓ$ и $m$ — квантовые числа). Обычно существуют три математические формы для радиальных функций $R (r)$ , которые можно выбрать в качестве отправной точки для расчета свойств атомов и молекул с большим количеством электронов:

Водородоподобные орбитали выводятся из точных решений уравнения Шредингера для одного электрона и ядра, для водородоподобного атома . Часть функции, которая зависит от расстояния r от ядра, имеет радиальные узлы и затухает как . $e^{-\альфа r}$
Орбиталь слейтеровского типа (STO) представляет собой форму без радиальных узлов, но распадается из ядра, как и водородоподобная орбиталь.
Форма орбитали гауссовского типа (гауссианы) не имеет радиальных узлов и затухает как . $e^{-\альфа r^{2}}$

Хотя водородоподобные орбитали все еще используются в качестве педагогических инструментов, появление компьютеров сделало STO предпочтительными для атомов и двухатомных молекул, поскольку комбинации STO могут заменить узлы в водородоподобных орбиталях. Гауссианы обычно используются в молекулах с тремя или более атомами. Хотя сами по себе они не так точны, как STO, комбинации многих гауссиан могут достичь точности водородоподобных орбиталей.

История

Термин «орбитальный» был введен Робертом С. Малликеном в 1932 году как сокращение от одноэлектронной орбитальной волновой функции . ^[10]^[11] Нильс Бор объяснил около 1913 года, что электроны могут вращаться вокруг компактного ядра с определенным угловым моментом. ^[12] Модель Бора была улучшением объяснений Эрнеста Резерфорда 1911 года , которые касались движения электрона вокруг ядра. Японский физик Хантаро Нагаока опубликовал гипотезу, основанную на орбите, для поведения электрона еще в 1904 году. ^[13] Каждая из этих теорий была построена на новых наблюдениях, начинающихся с простого понимания и становящихся все более правильными и сложными. Объяснение поведения этих электронных «орбит» было одной из движущих сил развития квантовой механики . ^[14]

Ранние модели

С открытием электрона Дж. Дж. Томсоном в 1897 году ^[15] стало ясно, что атомы не являются наименьшими строительными блоками природы , а скорее составными частицами. Недавно обнаруженная структура внутри атомов соблазнила многих представить, как составные части атома могут взаимодействовать друг с другом. Томсон предположил, что множественные электроны вращаются в орбитоподобных кольцах внутри положительно заряженного желеобразного вещества ^[16] , и между открытием электрона и 1909 годом эта « модель сливового пудинга » была наиболее широко принятым объяснением атомной структуры.

Вскоре после открытия Томсона Хантаро Нагаока предсказал другую модель электронной структуры. ^[13] В отличие от модели сливового пудинга, положительный заряд в «модели Сатурна» Нагаоки был сконцентрирован в центральном ядре, втягивая электроны в круговые орбиты, напоминающие кольца Сатурна. Мало кто обратил внимание на работу Нагаоки в то время, ^[17] и сам Нагаока осознал фундаментальный недостаток теории еще при ее зарождении, а именно, что классический заряженный объект не может поддерживать орбитальное движение, поскольку он ускоряется и, следовательно, теряет энергию из-за электромагнитного излучения. ^[18] Тем не менее, модель Сатурна оказалась более похожей на современную теорию, чем любая из ее современниц.

атом Бора

В 1909 году Эрнест Резерфорд обнаружил, что основная часть атомной массы плотно сконденсирована в ядре, которое также оказалось положительно заряженным. Из его анализа в 1911 году стало ясно, что модель сливового пудинга не может объяснить структуру атома. В 1913 году аспирант Резерфорда Нильс Бор предложил новую модель атома, в которой электроны вращались вокруг ядра с классическими периодами, но им разрешалось иметь только дискретные значения углового момента, квантованные в единицах ħ . ^[12] Это ограничение автоматически допускало только определенные энергии электронов. Модель атома Бора исправила проблему потери энергии при излучении из основного состояния (заявив, что ниже этого состояния нет), и, что более важно, объяснила происхождение спектральных линий.

После того, как Бор использовал объяснение Эйнштейна фотоэлектрического эффекта для связи уровней энергии в атомах с длиной волны испускаемого света, связь между структурой электронов в атомах и спектрами испускания и поглощения атомов стала все более полезным инструментом в понимании электронов в атомах. Наиболее заметной особенностью спектров испускания и поглощения (известных экспериментально с середины XIX века) было то, что эти атомные спектры содержали дискретные линии. Значение модели Бора состояло в том, что она связывала линии в спектрах испускания и поглощения с разницей в энергии между орбитами, которые электроны могли занимать вокруг атома. Однако Бору удалось достичь этого не путем придания электронам каких-то волновых свойств, поскольку идея о том, что электроны могут вести себя как волны материи, была высказана лишь одиннадцать лет спустя. Тем не менее, использование в модели Бора квантованных угловых моментов и, следовательно, квантованных уровней энергии стало значительным шагом на пути к пониманию электронов в атомах, а также значительным шагом на пути к развитию квантовой механики, поскольку она предположила, что квантованные ограничения должны учитывать все прерывистые уровни энергии и спектры в атомах.

С предположением де Бройля о существовании волн электронной материи в 1924 году и в течение короткого времени до полной обработки уравнения Шредингера 1926 года водородоподобных атомов , «длина волны» электрона Бора могла рассматриваться как функция его импульса; таким образом, вращающийся вокруг Бора электрон рассматривался как вращающийся по окружности с кратностью его половины длины волны. Модель Бора в течение короткого времени могла рассматриваться как классическая модель с дополнительным ограничением, предоставляемым аргументом «длины волны». Однако этот период был немедленно вытеснен полной трехмерной волновой механикой 1926 года. В нашем текущем понимании физики модель Бора называется полуклассической моделью из-за ее квантования углового момента, а не в первую очередь из-за ее связи с длиной волны электрона, которая появилась задним числом через дюжину лет после того, как была предложена модель Бора.

Модель Бора смогла объяснить спектры излучения и поглощения водорода . Энергии электронов в состояниях n = 1, 2, 3 и т. д. в модели Бора соответствуют энергиям современной физики. Однако это не объяснило сходства между различными атомами, как это выражено в периодической таблице, например, тот факт, что гелий (два электрона), неон (10 электронов) и аргон (18 электронов) демонстрируют схожую химическую инертность. Современная квантовая механика объясняет это в терминах электронных оболочек и подоболочек, каждая из которых может содержать число электронов, определяемое принципом исключения Паули . Таким образом, состояние n = 1 может содержать один или два электрона, в то время как состояние n = 2 может содержать до восьми электронов в подоболочках 2s и 2p. В гелии все состояния n = 1 полностью заняты; то же самое верно для n = 1 и n = 2 в неоне. В аргоне подоболочки 3s и 3p аналогично полностью заняты восемью электронами; Квантовая механика также допускает существование 3d-подоболочки, но она находится при более высокой энергии, чем 3s и 3p в аргоне (в отличие от ситуации для водорода), и остается пустой.

Современные концепции и связи с принципом неопределенности Гейзенберга

Сразу после того, как Гейзенберг открыл свой принцип неопределенности , ^[19] Бор отметил, что существование любого вида волнового пакета подразумевает неопределенность в частоте и длине волны волны, поскольку для создания самого пакета необходим разброс частот. ^[20] В квантовой механике, где все импульсы частиц связаны с волнами, именно образование такого волнового пакета локализует волну и, следовательно, частицу в пространстве. В состояниях, где квантово-механическая частица связана, она должна быть локализована как волновой пакет, а существование пакета и его минимальный размер подразумевают разброс и минимальное значение длины волны частицы, а значит, также импульса и энергии. В квантовой механике, поскольку частица локализуется в меньшей области пространства, связанный с ней сжатый волновой пакет требует все большего и большего диапазона импульсов и, следовательно, большей кинетической энергии. Таким образом, энергия связи для удержания или захвата частицы в меньшей области пространства неограниченно возрастает по мере уменьшения области пространства. Частицы не могут быть ограничены геометрической точкой в пространстве, поскольку для этого потребовался бы бесконечный импульс частицы.

В химии Эрвин Шредингер , Линус Полинг , Малликен и другие отметили, что следствием соотношения Гейзенберга было то, что электрон, как волновой пакет, не мог считаться имеющим точное местоположение на своей орбите. Макс Борн предположил, что положение электрона должно быть описано распределением вероятностей , которое было связано с нахождением электрона в некоторой точке волновой функции, которая описывала его связанный волновой пакет. Новая квантовая механика не давала точных результатов, а только вероятности возникновения множества возможных таких результатов. Гейзенберг считал, что путь движущейся частицы не имеет смысла, если мы не можем его наблюдать, как мы не можем наблюдать электроны в атоме.

В квантовой картине Гейзенберга, Шредингера и других число атомов Бора n для каждой орбитали стало известно как n-сфера ^{[ необходима ссылка ]} в трехмерном атоме и изображалось как наиболее вероятная энергия облака вероятностей волнового пакета электрона, окружающего атом.

Орбитальные названия

Орбитальная нотация и подоболочки

Орбиталям даны названия, которые обычно имеют вид:

X\,\mathrm {тип} \

где X — уровень энергии, соответствующий главному квантовому числу $n$ ; тип — строчная буква, обозначающая форму или подоболочку орбитали, соответствующую квантовому числу углового момента $ℓ$ .

Например, орбиталь 1s (произносится как отдельные цифры и буквы: «один» «есс») является самым низким энергетическим уровнем ( $n = 1$ ) и имеет угловое квантовое число $ℓ = 0$ , обозначаемое как s. Орбитали с $ℓ = 1, 2 и 3$ обозначаются как p, d и f соответственно.

Набор орбиталей для заданных n и $ℓ$ называется подоболочкой и обозначается

X\,\mathrm {тип} ^{y}\

Верхний индекс y показывает количество электронов в подоболочке. Например, обозначение 2p ⁴ указывает, что подоболочка 2p атома содержит 4 электрона. Эта подоболочка имеет 3 орбитали, каждая с n = 2 и $ℓ$ = 1.

Рентгеновская нотация

Существует также другая, менее распространенная система, которая все еще используется в рентгеновской науке, известная как рентгеновская нотация , которая является продолжением нотаций, использовавшихся до того, как орбитальная теория была хорошо понята. В этой системе главному квантовому числу присваивается буква, связанная с ним. Для $n = 1, 2, 3, 4, 5, ...$ буквы, связанные с этими числами, - K, L, M, N, O, ... соответственно.

Водородоподобные орбитали

Простейшими атомными орбиталями являются те, которые рассчитываются для систем с одним электроном, таких как атом водорода . Атом любого другого элемента, ионизированный до одного электрона (He ⁺ , Li ²⁺ и т. д.), очень похож на водород, и орбитали принимают ту же форму. В уравнении Шредингера для этой системы из одной отрицательной и одной положительной частицы атомные орбитали являются собственными состояниями оператора Гамильтона для энергии. Их можно получить аналитически, что означает, что полученные орбитали являются произведениями полиномиального ряда, а также экспоненциальной и тригонометрической функций . (см. атом водорода ).

Для атомов с двумя и более электронами основные уравнения могут быть решены только с использованием методов итеративного приближения. Орбитали многоэлектронных атомов качественно подобны орбиталям водорода, и в простейших моделях они принимаются имеющими тот же вид. Для более строгого и точного анализа необходимо использовать численные приближения.

Заданная (водородподобная) атомная орбиталь идентифицируется уникальными значениями трех квантовых чисел: $n$ , $ℓ$ и $m ℓ$ . Правила, ограничивающие значения квантовых чисел и их энергии (см. ниже), объясняют электронную конфигурацию атомов и периодическую таблицу .

Стационарные состояния ( квантовые состояния ) водородоподобного атома — это его атомные орбитали. Однако, в общем случае, поведение электрона не полностью описывается одной орбиталью. Электронные состояния лучше всего представляются зависящими от времени «смесями» ( линейными комбинациями ) нескольких орбиталей. См. Линейная комбинация атомных орбиталей молекулярный орбитальный метод .

Квантовое число $n$ впервые появилось в модели Бора , где оно определяет радиус каждой круговой электронной орбиты. Однако в современной квантовой механике $n$ определяет среднее расстояние электрона от ядра; все электроны с одинаковым значением n находятся на одном и том же среднем расстоянии. По этой причине говорят, что орбитали с одинаковым значением n составляют « оболочку ». Орбитали с одинаковым значением n , а также с одинаковым значением $ℓ$ связаны еще более тесно и, как говорят, составляют « подоболочку ».

Квантовые числа

Из-за квантово-механической природы электронов вокруг ядра атомные орбитали могут быть однозначно определены набором целых чисел, известных как квантовые числа. Эти квантовые числа встречаются только в определенных комбинациях значений, и их физическая интерпретация меняется в зависимости от того, используются ли реальные или комплексные версии атомных орбиталей.

Сложные орбитали

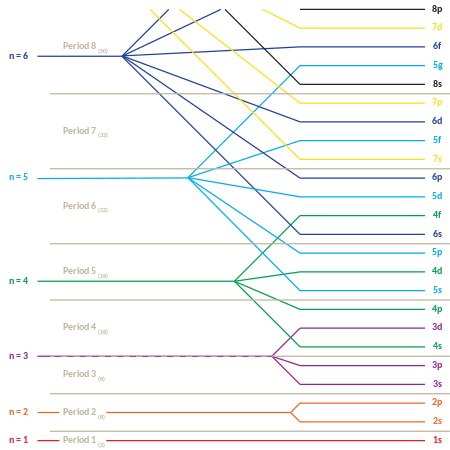
В физике наиболее распространенные орбитальные описания основаны на решениях для атома водорода, где орбитали задаются произведением радиальной функции и чистой сферической гармоники . Квантовые числа вместе с правилами, регулирующими их возможные значения, следующие:

Главное квантовое число $n$ описывает энергию электрона и всегда является положительным целым числом . Фактически, это может быть любое положительное целое число, но по причинам, обсуждаемым ниже, большие числа встречаются редко. Каждый атом имеет, как правило, много орбиталей, связанных с каждым значением n ; эти орбитали вместе иногда называются электронными оболочками .

Азимутальное квантовое число $ℓ$ описывает орбитальный угловой момент каждого электрона и является неотрицательным целым числом. В пределах оболочки, где $n$ — некоторое целое число $n 0$ , $ℓ$ варьируется по всем (целым) значениям, удовлетворяющим соотношению . Например, оболочка $n$ $= 1$ имеет только орбитали с , а оболочка $n$ $= 2$ имеет только орбитали с , и . Набор орбиталей, связанных с определенным значением $ℓ,$ иногда совместно называют подоболочкой . $0\leq \ell \leq n_{0}-1$ $\ell =0$ $\ell =0$ $\ell =1$

Магнитное квантовое число , , описывает проекцию орбитального углового момента вдоль выбранной оси. Оно определяет величину тока, циркулирующего вокруг этой оси, и орбитальный вклад в магнитный момент электрона через модель петли Ампера . ^[21] В подоболочке , получает целые значения в диапазоне . $m_{\ell }$ $\ell$ $m_{\ell }$ $-\ell \leq m_{\ell }\leq \ell$

Вышеуказанные результаты можно суммировать в следующей таблице. Каждая ячейка представляет подоболочку и перечисляет значения, доступные в этой подоболочке. Пустые ячейки представляют подоболочки, которые не существуют. $m_{\ell }$

Подоболочки обычно идентифицируются по их - и -значениям. представлено его числовым значением, но представлено буквой следующим образом: 0 представлено как 's', 1 как 'p', 2 как 'd', 3 как 'f' и 4 как 'g'. Например, можно говорить о подоболочке с и как о '2s подоболочке'. $n$ $\ell$ $n$ $\ell$ $n=2$ $\ell =0$

Каждый электрон также имеет угловой момент в форме квантово-механического спина, определяемого формулой спин s = ⁠1/2⁠ . Его проекция вдоль указанной оси задается спиновым магнитным квантовым числом , m _s , которое может быть + ⁠1/2⁠ или − ⁠1/2⁠ . Эти значения также называются «спин вверх» или «спин вниз» соответственно.

Принцип исключения Паули гласит, что никакие два электрона в атоме не могут иметь одинаковые значения всех четырех квантовых чисел. Если на орбитали с заданными значениями трех квантовых чисел ( $n$ , $ℓ$ , $m$ ) находятся два электрона, эти два электрона должны различаться проекцией спина m _s .

Вышеуказанные соглашения подразумевают предпочтительную ось (например, направление z в декартовых координатах), и они также подразумевают предпочтительное направление вдоль этой предпочтительной оси. В противном случае не было бы смысла различать $m = +1$ от $m = -1$ . Таким образом, модель наиболее полезна при применении к физическим системам, которые разделяют эти симметрии. Эксперимент Штерна-Герлаха — где атом подвергается воздействию магнитного поля — дает один из таких примеров. ^[22]

Реальные орбитали

Анимация непрерывно меняющихся суперпозиций между и орбиталями. Эта анимация не использует соглашение о фазах Кондона–Шортли.

{\text{p}}_{1}

{\text{p}}_{x}

Вместо описанных выше сложных орбиталей обычно, особенно в химической литературе, используют реальные атомные орбитали. Эти реальные орбитали возникают из простых линейных комбинаций сложных орбиталей. Используя соглашение о фазах Кондона-Шортли , реальные орбитали связаны с комплексными орбиталями таким же образом, как реальные сферические гармоники связаны с комплексными сферическими гармониками. Обозначая комплексную орбиталь с квантовыми числами , и , реальные орбитали можно определить как ^[23] $\psi _{n,\ell ,m}$ $n$ $л$ $м$ $\psi _{n,\ell ,m}^{\text{действительный}}$ $\psi _{n,\ell ,m}^{\text{real}}={\begin{cases}{\sqrt {2}}(-1)^{m}{\text{Im}}\left\{\psi _{n,\ell ,|m|}\right\}&{\text{ for }}m<0\\\psi _{n,\ell ,|m|}&{\text{ for }}m=0\\{\sqrt {2}}(-1)^{m}{\text{Re}}\left\{\psi _{n,\ell ,|m|}\right\}&{\text{ for }}m>0\end{cases}}={\begin{cases}{\frac {i}{\sqrt {2}}}\left(\psi _{n,\ell ,-|m|}-(-1)^{m}\psi _{n,\ell ,|m|}\right)&{\text{ для }}m<0\\\psi _{n,\ell ,|m|}&{\text{ для }}m=0\\{\frac {1}{\sqrt {2}}}\left(\psi _{n,\ell ,-|m|}+(-1)^{m}\psi _{n,\ell ,|m|}\right)&{\text{ для }}m>0\\\end{cases}}$

Если , с радиальной частью орбитали, это определение эквивалентно , где действительная сферическая гармоника связана либо с действительной, либо с мнимой частью комплексной сферической гармоники . $\psi _{n,\ell ,m}(r,\theta ,\phi )=R_{nl}(r)Y_{\ell }^{m}(\theta ,\phi )$ $R_{nl}(r)$ $\psi _{n,\ell ,m}^{\text{действительный}}(r,\theta ,\phi )=R_{nl}(r)Y_{\ell m}(\theta ,\phi )$ $Y_{\ell m}$ $Y_{\ell }^{m}$

Реальные сферические гармоники физически значимы, когда атом встроен в кристаллическое тело, в этом случае существует несколько предпочтительных осей симметрии, но нет одного предпочтительного направления. ^{[ требуется ссылка ]} Реальные атомные орбитали также чаще встречаются в учебниках по вводной химии и показаны в обычных орбитальных визуализациях. ^[24] В реальных водородоподобных орбиталях квантовые числа и имеют ту же интерпретацию и значение, что и их комплексные аналоги, но больше не являются хорошим квантовым числом (но его абсолютное значение является). $n$ $\ell$ $м$

Некоторые реальные орбитали получают особые названия, выходящие за рамки простого обозначения. Орбитали с квантовым числом, равным , называются орбиталями. При этом уже можно присваивать названия сложным орбиталям, например ; первый символ — это квантовое число, второй символ — это символ для этого конкретного квантового числа, а нижний индекс — это квантовое число. $\psi _{n,\ell ,m}$ $\ell$ $0,1,2,3,4,5,6\ldots$ ${\text{с, п, д, е, ж, з, я}}\ldots$ $2{\text{p}}_{\pm 1}=\psi _{2,1,\pm 1}$ $n$ $\ell$ $м$

В качестве примера того, как генерируются полные орбитальные имена для реальных орбиталей, можно вычислить . Из таблицы сферических гармоник , с . Тогда $\psi _{n,1,\pm 1}^{\text{реальный}}$ ${\textstyle \psi _{n,1,\pm 1}=R_{n,1}Y_{1}^{\pm 1}=\mp R_{n,1}{\sqrt {3/8\pi }}\cdot (x\pm iy)/r}$ $r={\sqrt {x^{2}+y^{2}+z^{2}}}$

{\begin{align}\psi _{n,1,+1}^{\text{real}}=&R_{n,1}{\sqrt {\frac {3}{4\pi }}}\cdot {\frac {x}{r}}\\\psi _{n,1,-1}^{\text{real}}=&R_{n,1}{\sqrt {\frac {3}{4\pi }}}\cdot {\frac {y}{r}}\end{align}}

Аналогично . Как более сложный пример: ${\textstyle \psi _{n,1,0}=R_{n,1}{\sqrt {3/4\pi }}\cdot z/r}$

\psi _{n,3,+1}^{\text{real}}=R_{n,3}{\frac {1}{4}}{\sqrt {\frac {21}{2\pi }}}\cdot {\frac {x\cdot (5z^{2}-r^{2})}{r^{3}}}

Во всех этих случаях мы генерируем декартову метку для орбитали, исследуя и сокращая полином в , и , появляющийся в числителе. Мы игнорируем любые члены в полиноме, за исключением члена с наивысшим показателем в . Затем мы используем сокращенный полином в качестве нижнего индекса для атомного состояния, используя ту же номенклатуру, что и выше, для обозначения и квантовых чисел. ^[^{необходима цитата}^] $x$ $у$ $z$ $z,r$ $z$ $n$ $\ell$

{\begin{aligned}\psi _{n,1,-1}^{\text{real}}=&n{\text{p}}_{y}={\frac {i}{\sqrt {2}}}\left(n{\text{p}}_{-1}+n{\text{p}}_{+1}\right)\\\psi _{n,1,0}^{\text{real}}=&n{\text{p}}_{z}=2{\text{p}}_{0}\\\psi _{n,1,+1}^{\text{real}}=&n{\text{p}}_{x}={\frac {1}{\sqrt {2}}}\left(n{\text{p}}_{-1}-n{\text{p}}_{+1}\right)\\\psi _{n,3,+1}^{\text{real}}=&nf_{xz^{2}}={\frac {1}{\sqrt {2}}}\left(nf_{-1}-nf_{+1}\right)\end{aligned}}

Выражение выше использует соглашение о фазе Кондона–Шортли , которое предпочитают квантовые физики. ^[25]^[26] Существуют и другие соглашения для фазы сферических гармоник. ^[27]^[28] В соответствии с этими различными соглашениями орбитали и могут выглядеть, например, как сумма и разность и , вопреки тому, что показано выше. ${\text{p}}_{x}$ ${\text{p}}_{y}$ ${\text{p}}_{+1}$ ${\text{p}}_{-1}$

Ниже приведен список названий этих декартовых полиномов для атомных орбиталей. ^[29]^[30] В литературе, похоже, нет ссылок на то, как сокращать длинные декартовы сферические гармонические полиномы, поэтому, похоже, нет консенсуса относительно наименования орбиталей или выше в соответствии с этой номенклатурой. ^[^{необходима ссылка}^] $\ell >3$ $g$

Формы орбиталей

Простые рисунки, показывающие орбитальные формы, предназначены для описания угловых форм областей в пространстве, где электроны, занимающие орбиталь, вероятно, будут находиться. Диаграммы не могут показать всю область, где может находиться электрон, поскольку согласно квантовой механике существует ненулевая вероятность нахождения электрона (почти) в любом месте пространства. Вместо этого диаграммы являются приблизительными представлениями граничных или контурных поверхностей , где плотность вероятности $| ψ(r, θ, φ) | 2$ имеет постоянное значение, выбранное так, чтобы существовала определенная вероятность (например, 90%) нахождения электрона внутри контура. Хотя $| ψ | 2$ как квадрат абсолютного значения всюду неотрицателен, знак волновой функции $ψ(r, θ, φ)$ часто указывается в каждой подобласти орбитальной картины.

Иногда функция $ψ$ изображается в виде графика, чтобы показать ее фазы, а не $| ψ(r, θ, φ) | 2$ , который показывает плотность вероятности, но не имеет фазы (которая теряется при взятии абсолютного значения, поскольку $ψ(r, θ, φ)$ является комплексным числом ). $| ψ(r, θ, φ) | 2$ Орбитальные графики, как правило, имеют менее сферические, более тонкие доли, чем графики $ψ(r, θ, φ)$ , но имеют такое же количество долей в тех же местах и в остальном узнаваемы. В этой статье для демонстрации фазы волновой функции показаны в основном графики $ψ(r, θ, φ)$ .

Лепестки можно рассматривать как картины интерференции стоячей волны между двумя вращающимися в противоположных направлениях, кольцевыми резонансными бегущими волновыми модами $m$ и $-$ $m$ ; проекция орбитали на плоскость xy имеет резонансную длину волны $m$ по окружности. Хотя это редко показывают, решения бегущей волны можно рассматривать как вращающиеся полосчатые торы; полосы представляют фазовую информацию. Для каждого $m$ существует два решения стоячей волны $⟨$ $m$ $⟩ + ⟨-$ $m$ $⟩$ и $⟨$ $m$ $⟩ - ⟨-$ $m$ $⟩$ . Если $m$ $= 0$ , орбиталь вертикальна, информация о вращении в противоположных направлениях неизвестна, и орбиталь симметрична относительно оси z . Если $ℓ$ $= 0,$ то нет мод, вращающихся в противоположных направлениях. Есть только радиальные моды, и форма сферически симметрична.

Узловые плоскости и узловые сферы — это поверхности, на которых плотность вероятности равна нулю. Количество узловых поверхностей контролируется квантовыми числами $n$ и $ℓ$ . Орбиталь с азимутальным квантовым числом $ℓ$ имеет $ℓ$ радиальных узловых плоскостей, проходящих через начало координат. Например, s-орбитали ( $ℓ = 0$ ) сферически симметричны и не имеют узловых плоскостей, тогда как p-орбитали ( $ℓ = 1$ ) имеют одну узловую плоскость между лепестками. Количество узловых сфер равно $n-ℓ-1$ , что согласуется с ограничением $ℓ \leq n-1$ на квантовые числа. Главное квантовое число контролирует общее количество узловых поверхностей, которое равно $n-1$ .^[31] Грубо говоря, $n$ — это энергия, $ℓ$ аналогично эксцентриситету , а $m$ — ориентация.

В общем, $n$ определяет размер и энергию орбитали для данного ядра; с ростом $n$ размер орбитали увеличивается. Более высокий заряд ядра $Z$ более тяжелых элементов заставляет их орбитали сжиматься по сравнению с более легкими, так что размер атома остается примерно постоянным, даже если число электронов увеличивается.

Также в общих чертах $ℓ$ определяет форму орбитали, а $m ℓ$ — ее ориентацию. Однако, поскольку некоторые орбитали описываются уравнениями в комплексных числах , форма иногда зависит также от $m ℓ$ . Вместе весь набор орбиталей для заданных $ℓ$ и $n$ заполняет пространство настолько симметрично, насколько это возможно, хотя и со все более сложными наборами лепестков и узлов.

Отдельные s-орбитали ( ) имеют форму сфер. Для $n$ $= 1$ это примерно сплошной шар (плотнее всего в центре и экспоненциально затухает наружу), но для $n$ $\geq 2$ каждая отдельная s-орбиталь состоит из сферически симметричных поверхностей, которые являются вложенными оболочками (т. е. «волновая структура» радиальная, также следуя синусоидальной радиальной составляющей). См. иллюстрацию поперечного сечения этих вложенных оболочек справа. s-орбитали для всех чисел $n$ являются единственными орбиталями с пучностью (областью высокой плотности волновой функции) в центре ядра. Все другие орбитали (p, d, f и т. д.) имеют угловой момент и, таким образом, избегают ядра (имея волновой узел в ядре). Недавно была предпринята попытка экспериментально визуализировать 1s- и 2p-орбитали в кристалле SrTiO ₃ с помощью сканирующей просвечивающей электронной микроскопии с энергодисперсионной рентгеновской спектроскопией. ^[32] Поскольку визуализация проводилась с использованием электронного пучка, кулоновское взаимодействие пучка с орбитой, которое часто называют эффектом ударного параметра, включено в результат (см. рисунок справа). $\ell =0$

Формы p-, d- и f-орбиталей описаны здесь словесно и показаны графически в таблице орбиталей ниже. Три p-орбитали для $n = 2$ имеют форму двух эллипсоидов с точкой касания в ядре (двухлепестковая форма иногда называется « гантелью » — есть две доли, направленные в противоположные стороны друг от друга). Три p-орбитали в каждой оболочке ориентированы под прямым углом друг к другу, что определяется их соответствующей линейной комбинацией значений $m ℓ$ . Общим результатом является доля, направленная вдоль каждого направления первичных осей.

Четыре из пяти d-орбиталей для $n = 3$ выглядят одинаково, каждая с четырьмя грушевидными лепестками, каждый лепесток касается двух других под прямым углом, а центры всех четырех лежат в одной плоскости. Три из этих плоскостей — это плоскости xy, xz и yz — лепестки находятся между парами первичных осей, а четвертая имеет центр вдоль самих осей x и y. Пятая и последняя d-орбиталь состоит из трех областей с высокой плотностью вероятности: тора между двумя грушевидными областями, расположенными симметрично на его оси z. Общая сумма из 18 направленных лепестков указывает в каждом направлении первичной оси и между каждой парой.

Существует семь f-орбиталей, каждая из которых имеет более сложную форму, чем d-орбитали.

Кроме того, как и в случае с s-орбиталями, отдельные p-, d-, f- и g-орбитали со значениями $n$ выше минимально возможного значения демонстрируют дополнительную радиальную узловую структуру, которая напоминает гармонические волны того же типа по сравнению с минимально возможной (или фундаментальной) модой волны. Как и в случае с s-орбиталями, это явление обеспечивает p-, d-, f- и g-орбитали при следующем максимально возможном значении $n$ (например, 3p-орбитали против фундаментальной 2p) дополнительным узлом в каждой доле. Еще более высокие значения $n$ еще больше увеличивают число радиальных узлов для каждого типа орбитали.

Формы атомных орбиталей в одноэлектронном атоме связаны с 3-мерными сферическими гармониками . Эти формы не являются уникальными, и любая линейная комбинация действительна, как преобразование в кубические гармоники , на самом деле возможно генерировать наборы, где все d имеют одинаковую форму, так же как $p x, p y,$ и $p z$ имеют одинаковую форму. ^[33]^[34]

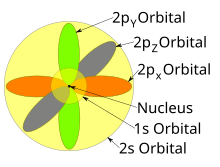
Хотя отдельные орбитали чаще всего показываются независимыми друг от друга, орбитали сосуществуют вокруг ядра в одно и то же время. Также в 1927 году Альбрехт Унзельд доказал, что если суммировать электронную плотность всех орбиталей определенного азимутального квантового числа $ℓ$ одной и той же оболочки $n$ (например, всех трех 2p-орбиталей или всех пяти 3d-орбиталей), где каждая орбиталь занята электроном или каждая занята электронной парой, то вся угловая зависимость исчезает; то есть результирующая общая плотность всех атомных орбиталей в этой подоболочке (с одинаковым $ℓ$ ) является сферической. Это известно как теорема Унзельда .

Таблица орбиталей

В этой таблице показаны реальные водородоподобные волновые функции для всех атомных орбиталей до 7s, и, следовательно, охватывают занятые орбитали в основном состоянии всех элементов в периодической таблице до радия и некоторых за ее пределами. Графики "ψ" показаны с фазами волновой функции − и +, показанными двумя разными цветами (произвольно красным и синим). Орбиталь $p$ $z$ такая же, как орбиталь $p$ $0$ , но $p$ $x$ и $p$ $y$ образованы путем взятия линейных комбинаций орбиталей $p$ $+1$ и $p$ $-1$ (именно поэтому они перечислены под меткой $m$ $= \pm1$ ). Кроме того, $p$ $+1$ и $p$ $-1$ не имеют той же формы, что и $p$ $0$ , поскольку они являются чистыми сферическими гармониками .

* Элементы с электронами 6f, 7d или 7f пока не обнаружены.

† Элементы с электронами 7p были обнаружены, но их электронные конфигурации только предсказаны — за исключением исключительного Lr , который заполняет 7p ¹ вместо 6d ¹ .

‡ Для элементов, у которых наивысшая занятая орбиталь является 6d-орбиталью, подтверждены только некоторые электронные конфигурации. ( Mt , Ds , Rg и Cn по-прежнему отсутствуют).

Это действительные орбитали, обычно используемые в химии. Только орбитали, где являются собственными состояниями оператора орбитального углового момента, . Столбцы с являются комбинациями двух собственных состояний. Смотрите сравнение на следующем рисунке : $m=0$ ${\hat {L}}_{z}$ $m=\pm 1,\pm 2,\cdots$

Качественное понимание форм

Формы атомных орбиталей можно качественно понять, рассмотрев аналогичный случай стоячих волн на круглом барабане . ^[35] Чтобы увидеть аналогию, среднее колебательное смещение каждой части мембраны барабана от точки равновесия за многие циклы (мера средней скорости и импульса мембраны барабана в этой точке) должно рассматриваться относительно расстояния этой точки от центра головки барабана. Если это смещение принять как аналогичное вероятности нахождения электрона на заданном расстоянии от ядра, то будет видно, что многочисленные моды вибрирующего диска образуют узоры, которые отслеживают различные формы атомных орбиталей. Основная причина этого соответствия заключается в том факте, что распределение кинетической энергии и импульса в волне вещества предсказывает, где будет находиться частица, связанная с волной. То есть вероятность обнаружения электрона в заданном месте также является функцией среднего импульса электрона в этой точке, поскольку высокий импульс электрона в заданном положении имеет тенденцию «локализировать» электрон в этом положении посредством свойств электронных волновых пакетов ( подробности механизма см. в принципе неопределенности Гейзенберга ).

Это соотношение означает, что определенные ключевые особенности можно наблюдать как в модах мембраны барабана, так и в атомных орбиталях. Например, во всех модах, аналогичных s- орбиталям (верхний ряд на анимированной иллюстрации ниже), можно увидеть, что самый центр мембраны барабана вибрирует сильнее всего, что соответствует пучности во всех s -орбиталях в атоме. Эта пучность означает, что электрон, скорее всего, находится в физическом положении ядра (через которое он проходит прямо, не рассеиваясь и не ударяясь о него), поскольку он движется (в среднем) наиболее быстро в этой точке, что дает ему максимальный импульс.

Ментальная картина «планетной орбиты», наиболее близкая к поведению электронов на s -орбиталях, все из которых не имеют углового момента, возможно, представляет собой кеплеровскую орбиту с эксцентриситетом орбиты 1, но конечной большой осью, что физически невозможно (поскольку частицы должны были бы сталкиваться), но может быть представлено как предел орбит с равными большими осями, но увеличивающимся эксцентриситетом.

Ниже показаны несколько мод колебаний мембраны барабана и соответствующие волновые функции атома водорода. Можно рассмотреть соответствие, где волновые функции вибрирующей головки барабана являются двухкоординатной системой $ψ(r, θ)$ , а волновые функции вибрирующей сферы являются трехкоординатной системой $ψ(r, θ, φ)$ .

барабанные моды s-типа и волновые функции
Режим барабана $u_{01}$
Режим барабана $u_{02}$
Режим барабана $u_{03}$
Волновая функция 1s-орбитали (действительная часть, 2D-разрез ) $r_{\mathrm {max} }=2a_{0}$
Волновая функция 2s-орбитали (действительная часть, 2D-разрез, ) $r_{\mathrm {max} }=10a_{0}$
Волновая функция 3s-орбитали (действительная часть, 2D-разрез ) $r_{\mathrm {max} }=20a_{0}$

Ни один из других наборов мод в мембране барабана не имеет центральной пучности, и во всех них центр барабана не движется. Они соответствуют узлу в ядре для всех не- s -орбиталей в атоме. Все эти орбитали имеют некоторый угловой момент, и в планетарной модели они соответствуют частицам на орбите с эксцентриситетом меньше 1,0, так что они не проходят прямо через центр первичного тела, а держатся на некотором расстоянии от него.

Кроме того, моды барабана, аналогичные p- и d- модам в атоме, демонстрируют пространственную нерегулярность вдоль различных радиальных направлений от центра барабана, тогда как все моды, аналогичные s- модам, идеально симметричны в радиальном направлении. Свойства нерадиальной симметрии не- s -орбиталей необходимы для локализации частицы с угловым моментом и волновой природой на орбитали, где она должна стремиться держаться подальше от центральной силы притяжения, поскольку любая частица, локализованная в точке центрального притяжения, может не иметь углового момента. Для этих мод волны в барабанной головке стремятся избегать центральной точки. Такие особенности снова подчеркивают, что формы атомных орбиталей являются прямым следствием волновой природы электронов.

барабанные моды p-типа и волновые функции
Режим барабана $u_{11}$
Режим барабана $u_{12}$
Режим барабана $u_{13}$
Волновая функция 2p-орбитали (действительная часть, 2D-разрез ) $r_{\mathrm {max} }=10a_{0}$
Волновая функция 3p-орбитали (действительная часть, 2D-разрез ) $r_{\mathrm {max} }=20a_{0}$
Волновая функция 4p-орбитали (действительная часть, 2D-разрез ) $r_{\mathrm {max} }=25a_{0}$

барабанные режимы типа d
Режим барабана $u_{21}$
Режим барабана $u_{22}$
Режим барабана $u_{23}$

Орбитальная энергия

В атомах с одним электроном ( водородподобный атом ) энергия орбитали (и, следовательно, любого электрона на орбитали) определяется в основном . Орбиталь имеет наименьшую возможную энергию в атоме. Каждое последовательно более высокое значение имеет более высокую энергию, но разница уменьшается по мере увеличения. При высоком энергия становится настолько высокой, что электрон может легко покинуть атом. В одноэлектронных атомах все уровни с различными в пределах заданного вырождены в приближении Шредингера и имеют одинаковую энергию. Это приближение немного нарушается в решении уравнения Дирака (где энергия зависит от $n$ и другого квантового числа $j$ ), а также из-за влияния магнитного поля ядра и эффектов квантовой электродинамики . Последние вызывают крошечные различия в энергии связи, особенно для s- электронов, которые приближаются к ядру, поскольку они чувствуют очень немного другой ядерный заряд, даже в одноэлектронных атомах; см. сдвиг Лэмба . $n$ $n=1$ $n$ $n$ $n$ $\ell$ $n$

В атомах с несколькими электронами энергия электрона зависит не только от его орбитали, но и от его взаимодействий с другими электронами. Эти взаимодействия зависят от деталей его пространственного распределения вероятностей, и поэтому уровни энергии орбиталей зависят не только от , но и от . Более высокие значения связаны с более высокими значениями энергии; например, состояние 2p выше, чем состояние 2s. Когда , увеличение энергии орбитали становится настолько большим, что подталкивает энергию орбитали выше энергии s-орбитали в следующей более высокой оболочке; когда энергия подталкивается в оболочку на две ступени выше. Заполнение 3d-орбиталей не происходит, пока не будут заполнены 4s-орбитали. $n$ $\ell$ $\ell$ $\ell =2$ $\ell =3$

Увеличение энергии для подоболочек с увеличивающимся угловым моментом в более крупных атомах обусловлено эффектами взаимодействия электронов между собой, и оно, в частности, связано со способностью электронов с низким угловым моментом более эффективно проникать к ядру, где они подвергаются меньшему экранированию от заряда промежуточных электронов. Таким образом, в атомах с более высоким атомным номером электроны становятся все более и более определяющим фактором в их энергии, а главные квантовые числа электронов становятся все менее и менее важными в их энергетическом размещении. $\ell$ $n$

Последовательность энергий первых 35 подоболочек (например, 1s, 2p, 3d и т. д.) приведена в следующей таблице. Каждая ячейка представляет подоболочку с и , заданными ее индексами строки и столбца соответственно. Число в ячейке является позицией подоболочки в последовательности. Для линейного списка подоболочек с точки зрения увеличения энергий в многоэлектронных атомах см. раздел ниже. $n$ $\ell$

Примечание: пустые ячейки указывают на несуществующие подуровни, тогда как числа, выделенные курсивом, указывают на подуровни, которые могли бы (потенциально) существовать, но не содержат электронов ни в одном из известных в настоящее время элементов.

Размещение электронов и периодическая таблица

Атомные орбитали и строение периодической таблицы

Несколько правил регулируют размещение электронов на орбиталях ( электронная конфигурация ). Первое гласит, что никакие два электрона в атоме не могут иметь одинаковый набор значений квантовых чисел (это принцип исключения Паули ). Эти квантовые числа включают три, которые определяют орбитали, а также спиновое магнитное квантовое число $m s$ . Таким образом, два электрона могут занимать одну орбиталь, если они имеют разные значения $m s$ . Поскольку $m s$ принимает одно из двух значений ( ⁠1/2⁠ или ⁠-1/2⁠ ), максимум два электрона могут занимать каждую орбиталь.

Кроме того, электрон всегда стремится упасть в состояние с наименьшей возможной энергией. Он может занять любую орбиталь, пока это не нарушает принцип исключения Паули, но если доступны орбитали с более низкой энергией, это состояние нестабильно. Электрон в конечном итоге потеряет энергию (испуская фотон ) и упадет на более низкую орбиталь. Таким образом, электроны заполняют орбитали в порядке, указанном энергетической последовательностью, приведенной выше.

Это поведение отвечает за структуру периодической таблицы . Таблица может быть разделена на несколько рядов (называемых «периодами»), пронумерованных, начиная с 1 сверху. Известные в настоящее время элементы занимают семь периодов. Если определенный период имеет номер i , он состоит из элементов, чьи самые внешние электроны попадают в i- ю оболочку. Нильс Бор был первым, кто предположил (1923), что периодичность в свойствах элементов может быть объяснена периодическим заполнением электронных энергетических уровней, что приводит к электронной структуре атома. ^[36]

Периодическую таблицу также можно разделить на несколько пронумерованных прямоугольных « блоков ». Элементы, принадлежащие данному блоку, имеют следующую общую черту: их электроны с самой высокой энергией принадлежат одному и тому же $ℓ$ -состоянию (но $n$ , связанное с этим $ℓ$ -состоянием, зависит от периода). Например, два самых левых столбца составляют «s-блок». Самые внешние электроны Li и Be соответственно принадлежат к подоболочке 2s, а электроны Na и Mg — к подоболочке 3s.

Ниже приведен порядок заполнения орбиталей «подоболочки», который также дает порядок «блоков» в периодической таблице:

1с, 2с, 2п, 3с, 3п, 4с, 3д, 4п, 5с, 4д, 5п, 6с, 4ф, 5д, 6п, 7с, 5ф, 6д, 7п

«Периодическая» природа заполнения орбиталей, а также возникновение «блоков» s , p , d и f становится более очевидной, если этот порядок заполнения представить в матричной форме, при этом возрастающие главные квантовые числа начинают новые строки («периоды») в матрице. Затем каждая подоболочка (состоящая из первых двух квантовых чисел) повторяется столько раз, сколько требуется для каждой пары электронов, которые она может содержать. Результатом является сжатая периодическая таблица, в которой каждая запись представляет два последовательных элемента:

Хотя это общий порядок заполнения орбиталей согласно правилу Маделунга, существуют исключения, и фактические электронные энергии каждого элемента также зависят от дополнительных деталей атомов (см. Электронная конфигурация § Атомы: принцип Ауфбау и правило Маделунга ).

Число электронов в электрически нейтральном атоме увеличивается с атомным номером . Электроны на внешней оболочке, или валентные электроны , как правило, отвечают за химическое поведение элемента. Элементы, которые содержат одинаковое число валентных электронов, могут быть сгруппированы вместе и демонстрировать схожие химические свойства.

Релятивистские эффекты

Для элементов с высоким атомным номером $Z$ эффекты относительности становятся более выраженными, и особенно это касается s-электронов, которые движутся с релятивистскими скоростями, проникая через экранирующие электроны вблизи ядра атомов с высоким $Z.$ Это релятивистское увеличение импульса для высокоскоростных электронов вызывает соответствующее уменьшение длины волны и сжатие 6s-орбиталей относительно 5d-орбиталей (по сравнению с соответствующими s- и d-электронами в более легких элементах в том же столбце периодической таблицы); это приводит к тому, что 6s-валентные электроны становятся более энергичными.

Примерами значительных физических результатов этого эффекта являются пониженная температура плавления ртути (что является результатом того, что 6s-электроны не доступны для образования металлических связей) и золотистый цвет золота и цезия . ^[37]

В модели Бора электрон $n = 1$ имеет скорость, заданную выражением , где $Z$ — атомный номер, — постоянная тонкой структуры , а $c$ — скорость света. Таким образом, в нерелятивистской квантовой механике любой атом с атомным номером больше 137 потребовал бы, чтобы его 1s-электроны двигались быстрее скорости света. Даже в уравнении Дирака , которое учитывает релятивистские эффекты, волновая функция электрона для атомов с является колебательной и неограниченной . Значимость элемента 137, также известного как унтрисептий , была впервые отмечена физиком Ричардом Фейнманом . Элемент 137 иногда неформально называют фейнманием (символ Fy). ^[38] Однако приближение Фейнмана не может предсказать точное критическое значение $Z$ из-за неточечной природы заряда ядра и очень малого орбитального радиуса внутренних электронов, что приводит к потенциалу, наблюдаемому внутренними электронами, который фактически меньше $Z$ . Критическое значение $Z$ , которое делает атом нестабильным по отношению к сильному полевому пробою вакуума и образованию электронно-позитронных пар, не достигается, пока $Z$ не станет около 173. Эти условия не наблюдаются, за исключением кратковременных столкновений очень тяжелых ядер, таких как свинец или уран, в ускорителях, где, как утверждается, наблюдается такое электронно-позитронное образование в результате этих эффектов. $v=Z\alpha c$ $\alpha$ $Z>137$

В релятивистских орбитальных плотностях нет узлов, хотя отдельные компоненты волновой функции будут иметь узлы. ^[39]

pp гибридизация (предполагаемая)

В позднем периоде 8 элементов ожидается существование гибрида 8p 3/2 и 9p 1/2, [ 40 _] где _"^3/2 " и "1/2" относятся к полному квантовому числу углового момента . Этот гибрид "pp" может быть ответственным за p-блок периода из-за свойств, аналогичных p-подоболочкам в обычных валентных оболочках . Энергетические уровни 8p _3/2 и 9p _1/2 сближаются из-за релятивистских спин-орбитальных эффектов ; 9s-подоболочка также должна участвовать, поскольку ожидается, что эти элементы будут аналогичны соответствующим 5p-элементам от индия до ксенона .

Переходы между орбиталями

Связанные квантовые состояния имеют дискретные уровни энергии. Применительно к атомным орбиталям это означает, что различия в энергии между состояниями также дискретны. Таким образом, переход между этими состояниями (т. е. поглощение или испускание фотона электроном) может произойти только в том случае, если фотон имеет энергию, соответствующую точной разнице энергий между указанными состояниями.

Рассмотрим два состояния атома водорода:

Состояние $n = 1$ , $ℓ = 0$ , $m ℓ = 0$ и $m s = + ⁠ 1 / 2 ⁠$
Состояние $n = 2$ , $ℓ = 0$ , $m ℓ = 0$ и $m s = - ⁠ 1 / 2 ⁠$

Согласно квантовой теории, состояние 1 имеет фиксированную энергию $E 1$ , а состояние 2 имеет фиксированную энергию $E 2$ . Теперь, что произойдет, если электрон из состояния 1 перейдет в состояние 2? Для этого электрон должен получить энергию, равную точно $E 2 - E 1$ . Если электрон получает энергию, которая меньше или больше этого значения, он не может перейти из состояния 1 в состояние 2. Теперь предположим, что мы облучаем атом широким спектром света. Фотоны, достигающие атома, которые имеют энергию точно $E 2 - E 1 ,$ будут поглощены электроном в состоянии 1, и этот электрон перейдет в состояние 2. Однако фотоны, которые имеют большую или меньшую энергию, не могут быть поглощены электроном, потому что электрон может перейти только на одну из орбиталей, он не может перейти в состояние между орбиталями. В результате атом будет поглощать только фотоны определенной частоты. Это создает линию в спектре, известную как линия поглощения, которая соответствует разнице энергий между состояниями 1 и 2.

Таким образом, атомная орбитальная модель предсказывает линейчатые спектры, которые наблюдаются экспериментально. Это одно из главных подтверждений атомной орбитальной модели.

Тем не менее, атомная орбитальная модель является приближением к полной квантовой теории, которая признает только многоэлектронные состояния. Предсказания линейчатых спектров полезны качественно, но не являются количественно точными для атомов и ионов, отличных от тех, которые содержат только один электрон.

Смотрите также

Таблица электронной конфигурации атома

Ссылки

^ Орчин, Милтон; Макомбер, Роджер С.; Пинхас, Аллан; Уилсон, Р. Маршалл (2005). "1. Теория атомных орбиталей" (PDF) . Словарь и концепции органической химии (2-е изд.). Wiley. Архивировано (PDF) из оригинала 9 октября 2022 г.
^ Daintith, J. (2004). Оксфордский словарь химии. Нью-Йорк: Oxford University Press. С. 407–409. ISBN 978-0-19-860918-6.
^ Гриффитс, Дэвид (1995). Введение в квантовую механику . Prentice Hall. стр. 190–191. ISBN 978-0-13-124405-4.
^ Левин, Айра (2000). Квантовая химия (5-е изд.). Prentice Hall. стр. 144–145. ISBN 978-0-13-685512-5.
^ Laidler, Keith J.; Meiser, John H. (1982). Физическая химия . Benjamin/Cummings. стр. 488. ISBN 978-0-8053-5682-3.
^ Аткинс, Питер; де Паула, Хулио; Фридман, Рональд (2009). Кванты, материя и изменение: молекулярный подход к физической химии. Oxford University Press. стр. 106. ISBN 978-0-19-920606-3.
^ Фейнман, Ричард; Лейтон, Роберт Б.; Сэндс, Мэтью (2006). Лекции Фейнмана по физике – окончательное издание, том 1, вып. 6. Pearson PLC, Addison Wesley. стр. 11. ISBN 978-0-8053-9046-9.
^ Роджер Пенроуз , Дорога к реальности
^ Левин, Айра Н. (1991). Квантовая химия (4-е изд.). Prentice-Hall. стр. 262. ISBN 0-205-12770-3. Следовательно, волновая функция системы одинаковых взаимодействующих частиц не должна различать частицы.
^ Малликен, Роберт С. (июль 1932 г.). «Электронные структуры многоатомных молекул и валентность. II. Общие положения». Physical Review . 41 (1): 49–71. Bibcode :1932PhRv...41...49M. doi :10.1103/PhysRev.41.49.
^ Мюррелл, Джон Н. (5 сентября 2012 г.). «Истоки и поздние разработки теории молекулярных орбиталей». Международный журнал квантовой химии . 112 (17): 2875–2879. doi :10.1002/qua.23293. ISSN 0020-7608.
^ ab Bohr, Niels (1913). "О строении атомов и молекул". Philosophical Magazine . 26 (1): 476. Bibcode :1914Natur..93..268N. doi :10.1038/093268a0. S2CID 3977652.
^ ab Nagaoka, Hantaro (май 1904 г.). «Кинетика системы частиц, иллюстрирующая линейный и полосчатый спектры и явления радиоактивности». Philosophical Magazine . 7 (41): 445–455. doi :10.1080/14786440409463141. Архивировано из оригинала 27 ноября 2017 г. . Получено 30 мая 2009 г. .
^ Брайсон, Билл (2003). Краткая история почти всего . Broadway Books. стр. 141–143. ISBN 978-0-7679-0818-4.
^ Томсон, Дж. Дж. (1897). «Катодные лучи». Philosophical Magazine . 44 (269): 293. doi :10.1080/14786449708621070.
^ Томсон, Дж. Дж. (1904). «О структуре атома: исследование устойчивости и периодов колебаний ряда корпускул, расположенных на равных интервалах по окружности круга; с применением результатов к теории атомной структуры» (выдержка из статьи) . Philosophical Magazine . Серия 6. 7 (39): 237–265. doi :10.1080/14786440409463107.
^ Родс, Ричард (1995). Создание атомной бомбы. Simon & Schuster. стр. 50–51. ISBN 978-0-684-81378-3.
^ Нагаока, Хантаро (май 1904 г.). «Кинетика системы частиц, иллюстрирующая линейный и полосчатый спектры и явления радиоактивности». Philosophical Magazine . 7 (41): 446. doi :10.1080/14786440409463141. Архивировано из оригинала 27 ноября 2017 г. Получено 30 мая 2009 г.
^ Гейзенберг, В. (март 1927 г.). «Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik». Zeitschrift für Physik A. 43 (3–4): 172–198. Бибкод : 1927ZPhy...43..172H. дои : 10.1007/BF01397280. S2CID 122763326.
↑ Бор, Нильс (апрель 1928 г.). «Квантовый постулат и недавнее развитие атомной теории». Nature . 121 (3050): 580–590. Bibcode :1928Natur.121..580B. doi : 10.1038/121580a0 .
^ Грейнер, Вальтер (1994). Квантовая механика: Введение (2-е исправленное изд.). Нью-Йорк, Берлин, Гейдельберг: Springer-Verlag. С. 163. ISBN 978-0-387-58080-7.
^ Герлах, В.; Стерн, О. (1922). «Магнитный момент сильбератомов». Zeitschrift für Physik . 9 (1): 353–355. Бибкод : 1922ZPhy....9..353G. дои : 10.1007/BF01326984. S2CID 126109346.
^ Thaller, Bernd (2004). Advanced visual quantum mechanics . Нью-Йорк: Springer/TELOS. ISBN 978-0387207773.
^ Петруччи, Ральф; Херринг, Ф.; Мадура, Джеффри; Биссоннетт, Кэри (2016). Общая химия: принципы и современные приложения (11-е изд.). [Место публикации не указано]: Prentice Hall. ISBN 978-0133897319.
^ Мессия, Альберт (1999). Квантовая механика: два тома, объединенные в один (Два тома, объединенные в один, несокращенное переиздание). Минеола, Нью-Йорк: Довер. ISBN 978-0-486-40924-5.
^ Клод Коэн-Таннуджи; Бернар Диу; Франк Лалоэ; и др. (1996). Квантовая механика . Перевод с французского Сьюзан Рейд Хемли. Wiley-Interscience. ISBN 978-0-471-56952-7.
^ Левин, Айра (2014). Квантовая химия (7-е изд.). Pearson Education. стр. 141–2. ISBN 978-0-321-80345-0.
^ Бланко, Мигель А.; Флорес, М.; Бермехо, М. (декабрь 1997 г.). «Оценка матриц вращения в базисе реальных сферических гармоник». Журнал молекулярной структуры: THEOCHEM . 419 (1–3): 19–27. doi :10.1016/S0166-1280(97)00185-1.
^ Общая химия: принципы и современные приложения . [Место издания не указано]: Prentice Hall. 2016. ISBN 978-0133897319.
^ Фридман (1964). "Формы f-орбиталей". J. Chem. Educ . 41 (7): 354. Bibcode :1964JChEd..41..354F. doi :10.1021/ed041p354.
^ Стэнли Рэймс (1963). Волновая механика электронов в металлах. North-Holland Publishing Company - Амстердам. стр. 39.
^ ab Jeong, Jong Seok; Odlyzko, Michael L.; Xu, Peng; Jalan, Bharat; Mkhoyan, K. Andre (26 апреля 2016 г.). «Исследование остовно-электронных орбиталей с помощью сканирующей просвечивающей электронной микроскопии и измерение делокализации возбуждений остовного уровня». Physical Review B. 93 ( 16): 165140. Bibcode : 2016PhRvB..93p5140J. doi : 10.1103/PhysRevB.93.165140 .
^ Пауэлл, Ричард Э. (1968). "Пять эквивалентных d-орбиталей". Журнал химического образования . 45 (1): 45. Bibcode : 1968JChEd..45...45P. doi : 10.1021/ed045p45.
^ Кимбалл, Джордж Э. (1940). «Направленная валентность». Журнал химической физики . 8 (2): 188. Bibcode : 1940JChPh...8..188K. doi : 10.1063/1.1750628.
^ Cazenave, Lions, T., P.; Lions, PL (1982). «Орбитальная устойчивость стоячих волн для некоторых нелинейных уравнений Шредингера». Communications in Mathematical Physics . 85 (4): 549–561. Bibcode :1982CMaPh..85..549C. doi :10.1007/BF01403504. S2CID 120472894.{{cite journal}}: CS1 maint: multiple names: authors list (link)
^ Бор, Нильс (1923). «Über die Anwendung der Quantumtheorie auf den Atombau. I». Zeitschrift für Physik . 13 (1): 117. Бибкод : 1923ZPhy...13..117B. дои : 10.1007/BF01328209. S2CID 123582460.
^ Лоуэр, Стивен. «Учебник по квантовой теории атома».
^ Полякофф, Мартин; Тан, Саманта (9 февраля 2015 г.). «Периодическая таблица: икона и вдохновение». Philosophical Transactions of the Royal Society A. 373 ( 2037): 20140211. Bibcode : 2015RSPTA.37340211P. doi : 10.1098/rsta.2014.0211 . PMID 25666072.
^ Сабо, Аттила (1969). «Контурные диаграммы для релятивистских орбиталей». Журнал химического образования . 46 (10): 678. Bibcode : 1969JChEd..46..678S. doi : 10.1021/ed046p678.
^ Фрике, Буркхард (1975). Сверхтяжелые элементы: предсказание их химических и физических свойств. Структура и связь. Т. 21. С. 89–144. doi :10.1007/BFb0116498. ISBN 978-3-540-07109-9. Получено 4 октября 2013 г. {{cite book}}: |journal=проигнорировано ( помощь )

Маккоу, Чарльз С. (2015). Орбитали: с приложениями в атомных спектрах. Сингапур: World Scientific Publishing Company. ISBN 9781783264162.
Типлер, Пол; Ллевеллин, Ральф (2003). Современная физика (4-е изд.). Нью-Йорк: WH Freeman and Company. ISBN 978-0-7167-4345-3.
Шерри, Эрик (2007). Периодическая таблица, ее история и ее значение . Нью-Йорк: Oxford University Press. ISBN 978-0-19-530573-9.
Левин, Айра (2014). Квантовая химия (7-е изд.). Pearson Education. ISBN 978-0-321-80345-0.
Гриффитс, Дэвид (2000). Введение в квантовую механику (2-е изд.). Бенджамин Каммингс. ISBN 978-0-13-111892-8.
Коэн, Ирвин; Бастард, Томас (1966). «Атомные орбитали: ограничения и вариации». J. Chem. Educ . 43 (4): 187. Bibcode : 1966JChEd..43..187C. doi : 10.1021/ed043p187.

Внешние ссылки

На Викискладе есть медиафайлы по теме «Атомные орбитали» .

3D-изображение водородных орбиталей
Орбитрон, визуализация всех распространенных и необычных атомных орбиталей от 1s до 7g
Большой стол. Неподвижные изображения многих орбиталей.