Поле (математика)

Алгебраическая структура со сложением, умножением и делением

Правильный семиугольник нельзя построить, используя только линейку и циркуль ; это можно доказать , используя поле конструктивных чисел .

В математике поле — это множество , на котором определены сложение , вычитание , умножение и деление , которые ведут себя как соответствующие операции над рациональными и действительными числами . Таким образом, поле — это фундаментальная алгебраическая структура , которая широко используется в алгебре , теории чисел и многих других областях математики.

Наиболее известными полями являются поле рациональных чисел , поле действительных чисел и поле комплексных чисел . Многие другие поля, такие как поля рациональных функций , поля алгебраических функций , поля алгебраических чисел и p -адические поля , обычно используются и изучаются в математике, особенно в теории чисел и алгебраической геометрии . Большинство криптографических протоколов опираются на конечные поля , т. е. поля с конечным числом элементов .

Теория полей доказывает, что трисекция угла и квадратура круга не могут быть выполнены с помощью циркуля и линейки . Теория Галуа , посвященная пониманию симметрии расширений полей , дает элегантное доказательство теоремы Абеля–Руффини о том, что общие уравнения пятой степени не могут быть решены в радикалах .

Поля служат основополагающими понятиями в нескольких математических областях. Это включает в себя различные ветви математического анализа , которые основаны на полях с дополнительной структурой. Основные теоремы в анализе зависят от структурных свойств поля действительных чисел. Что наиболее важно для алгебраических целей, любое поле может использоваться в качестве скаляров для векторного пространства , которое является стандартным общим контекстом для линейной алгебры . Числовые поля , братья и сестры поля рациональных чисел, подробно изучаются в теории чисел . Функциональные поля могут помочь описать свойства геометрических объектов.

Определение

Неформально, поле — это множество, вместе с двумя операциями, определенными на этом множестве: операция сложения, записанная как a + b , и операция умножения, записанная как a ⋅ b , обе из которых ведут себя аналогично тому, как они ведут себя для рациональных чисел и действительных чисел , включая существование аддитивной обратной − a для всех элементов a и мультипликативной обратной b ⁻¹ для каждого ненулевого элемента b . Это позволяет также рассматривать так называемые обратные операции вычитания, a − b , и деления, a / b , путем определения:

а − б  := а + (− б ) ,

а / б  := а ⋅ б ⁻¹ .

Классическое определение

Формально поле — это множество F вместе с двумя бинарными операциями над F , называемыми сложением и умножением . ^[1] Бинарная операция над F — это отображение F × F → F , то есть соответствие, которое сопоставляет каждой упорядоченной паре элементов F однозначно определенный элемент F . ^{[2] [3]} Результат сложения a и b называется суммой a и b и обозначается a + b . Аналогично, результат умножения a и b называется произведением a и b и обозначается ab или a ⋅ b . Эти операции требуются для удовлетворения следующих свойств, называемых аксиомами поля .

Эти аксиомы должны выполняться для всех элементов a , b , c поля F :

• Ассоциативность сложения и умножения: a + ( b + c ) = ( a + b ) + c , и a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c .
• Коммутативность сложения и умножения: a + b = b + a и a ⋅ b = b ⋅ a .
• Аддитивное и мультипликативное тождество : существуют два различных элемента 0 и 1 в F, такие что a + 0 = a и a ⋅ 1 = a .
• Аддитивные обратные элементы : для каждого a из F существует элемент в F , обозначаемый − a , называемый аддитивным обратным элементом a , такой, что a + (− a ) = 0 .
• Мультипликативные обратные элементы : для любого a ≠ 0 в F существует элемент в F , обозначаемый как a ⁻¹ или 1/ a , называемый мультипликативным обратным элементом a , такой, что a ⋅ a ⁻¹ = 1 .
• Распределимость умножения относительно сложения: a ⋅ ( b + c ) = ( a ⋅ b ) + ( a ⋅ c ) .

Эквивалентное и более краткое определение таково: поле имеет две коммутативные операции, называемые сложением и умножением; оно является группой относительно сложения с 0 в качестве аддитивного тождества; ненулевые элементы образуют группу относительно умножения с 1 в качестве мультипликативного тождества; и умножение распределяется относительно сложения.

Еще более кратко: поле — это коммутативное кольцо , где 0 ≠ 1 и все ненулевые элементы обратимы относительно умножения.

Альтернативное определение

Поля также могут быть определены различными, но эквивалентными способами. В качестве альтернативы можно определить поле четырьмя бинарными операциями (сложение, вычитание, умножение и деление) и их требуемыми свойствами. Деление на ноль по определению исключено. ^[4] Чтобы избежать квантификаторов существования , поля можно определить двумя бинарными операциями (сложением и умножением), двумя унарными операциями (дающими соответственно аддитивные и мультипликативные обратные величины) и двумя нульарными операциями (константы 0 и 1 ). Затем эти операции подчиняются условиям, указанным выше. Избегание квантификаторов существования важно в конструктивной математике и вычислениях . ^[5] Можно эквивалентно определить поле теми же двумя бинарными операциями, одной унарной операцией (мультипликативной обратной величиной) и двумя (не обязательно различными) константами 1 и −1 , поскольку 0 = 1 + (−1) и − a = (−1) a . ^[a]

Примеры

Рациональные числа

Рациональные числа широко использовались задолго до разработки концепции поля. Это числа, которые можно записать в виде дробей a / b , где a и b — целые числа , а b ≠ 0. Аддитивная обратная дробь такой дроби равна − a / b , а мультипликативная обратная (при условии, что a ≠ 0 ) равна b / a , что можно увидеть следующим образом:

${\displaystyle {\frac {b}{a}}\cdot {\frac {a}{b}}={\frac {ba}{ab}}=1.}$

Абстрактно требуемые аксиомы поля сводятся к стандартным свойствам рациональных чисел. Например, закон дистрибутивности может быть доказан следующим образом: ^[6]

${\displaystyle {\begin{aligned}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}+{\frac {e}{f}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}\cdot {\frac {f}{f}}+{\frac {e}{f}}\cdot {\frac {d}{d}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {cf}{df}}+{\frac {ed}{fd}}\right)={\frac {a}{b}}\cdot {\frac {cf+ed}{df}}\\[6pt]={}&{\frac {a(cf+ed)}{bdf}}={\frac {acf}{bdf}}+{\frac {aed}{bdf}}={\frac {ac}{bd}}+{\frac {ae}{bf}}\\[6pt]={}&{\frac {a}{b}}\cdot {\frac {c}{d}}+{\frac {a}{b}}\cdot {\frac {e}{f}}.\end{aligned}}}$

Действительные и комплексные числа

Умножение комплексных чисел можно визуализировать геометрически с помощью вращений и масштабирований.

Действительные числа R , с обычными операциями сложения и умножения, также образуют поле. Комплексные числа C состоят из выражений

a + bi , где a , b действительны,

где i — мнимая единица , т. е. (недействительное) число, удовлетворяющее i ² = −1 . Сложение и умножение действительных чисел определяются таким образом, что выражения этого типа удовлетворяют всем аксиомам поля и, таким образом, справедливы для C. Например, распределительный закон обеспечивает

( а + би )( с + ди ) = ас + bci + ади + бди ² = ( ас − бд ) + ( бс + ад ) я .

Сразу видно, что это снова выражение указанного выше типа, и поэтому комплексные числа образуют поле. Комплексные числа можно геометрически представить как точки на плоскости , с декартовыми координатами, заданными действительными числами их описывающего выражения, или как стрелки от начала координат до этих точек, заданные их длиной и углом, заключенным в некотором определенном направлении. Сложение тогда соответствует объединению стрелок в интуитивный параллелограмм (сложение декартовых координат), а умножение — менее интуитивно — объединение вращения и масштабирования стрелок (сложение углов и умножение длин). Поля действительных и комплексных чисел используются в математике, физике, инженерии, статистике и многих других научных дисциплинах.

Конструируемые числа

Теорема о среднем геометрическом утверждает, что h ² = pq . Выбор q = 1 позволяет построить квадратный корень заданного конструктивного числа p .

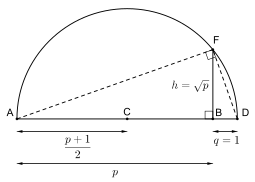
В древности несколько геометрических задач касались (не)возможности построения некоторых чисел с помощью циркуля и линейки . Например, грекам было неизвестно, что, в общем случае, невозможно трисекцию заданного угла таким образом. Эти задачи можно решить, используя поле конструктивных чисел . ^[7] Действительные конструктивные числа, по определению, являются длинами отрезков прямых, которые могут быть построены из точек 0 и 1 за конечное число шагов, используя только циркуль и линейку . Эти числа, наделенные полевыми операциями действительных чисел, ограниченными конструктивными числами, образуют поле, которое, собственно, включает поле Q рациональных чисел. На иллюстрации показано построение квадратных корней конструктивных чисел, не обязательно содержащихся в Q. Используя маркировку на иллюстрации, постройте отрезки AB , BD и полуокружность над AD (центр в средней точке C ), которая пересекает перпендикулярную линию, проходящую через B, в точке F , на расстоянии точно от B, когда BD имеет длину один. ${\displaystyle h={\sqrt {p}}}$

Не все действительные числа конструируемы. Можно показать, что — неконструируемое число, что подразумевает невозможность построения с помощью циркуля и линейки длины стороны куба с объемом 2 — еще одна проблема, поставленная древними греками. ${\displaystyle {\sqrt[{3}]{2}}}$

Поле с четырьмя элементами

В дополнение к знакомым системам счисления, таким как рациональные числа, существуют и другие, менее непосредственные примеры полей. Следующий пример — поле, состоящее из четырех элементов, называемых O , I , A , и B . Обозначение выбрано таким образом, что O играет роль элемента аддитивной идентичности (обозначаемого 0 в аксиомах выше), а I — мультипликативной идентичности (обозначаемого 1 в аксиомах выше). Аксиомы поля можно проверить, используя еще немного теории поля или прямым вычислением. Например,

A ⋅ ( B + A ) = A ⋅ I = A , что равно A ⋅ B + A ⋅ A = I + B = A , как того требует дистрибутивность.

Это поле называется конечным полем или полем Галуа с четырьмя элементами и обозначается F ₄ или GF(4) . ^[8] Подмножество , состоящее из O и I (выделено красным в таблицах справа), также является полем, известным как бинарное поле F ₂ или GF(2) .

Элементарные понятия

В этом разделе F обозначает произвольное поле, а a и b — произвольные элементы F.

Последствия определения

Имеем a ⋅ 0 = 0 и − a = (−1) ⋅ a . В частности, можно вывести аддитивную инверсию каждого элемента, как только узнаем −1 . ^[9]

Если ab = 0, то a или b должны быть равны 0 , поскольку, если a ≠ 0 , то b = ( a ⁻¹ a ) b = a ⁻¹ ( ab ) = a ⁻¹ ⋅ 0 = 0. Это означает, что каждое поле является областью целостности .

Кроме того, для любых элементов a и b справедливы следующие свойства :

−0 = 0

1 ⁻¹ = 1

(−(− а )) = а

(− а ) ⋅ б = а ⋅ (− б ) = −( а ⋅ б )

( а ⁻¹ ) ⁻¹ = а, если а ≠ 0

Аддитивные и мультипликативные группы поля

Аксиомы поля F подразумевают, что оно является абелевой группой относительно сложения. Эта группа называется аддитивной группой поля и иногда обозначается как ( F , +), хотя обозначение ее просто как F может привести к путанице.

Аналогично, ненулевые элементы F образуют абелеву группу относительно умножения, называемую мультипликативной группой и обозначаемую либо просто , либо F ^× . ${\displaystyle (F\smallsetminus \{0\},\cdot )}$ ${\displaystyle F\smallsetminus \{0\}}$

Таким образом, поле может быть определено как множество F, снабженное двумя операциями, обозначаемыми как сложение и умножение, такими, что F является абелевой группой относительно сложения, является абелевой группой относительно умножения (где 0 является единичным элементом сложения), и умножение является дистрибутивным относительно сложения. ^[b] Поэтому некоторые элементарные утверждения о полях могут быть получены путем применения общих фактов о группах . Например, аддитивные и мультипликативные обратные − a и a ⁻¹ однозначно определяются a . ${\displaystyle F\smallsetminus \{0\}}$

Требование 1 ≠ 0 налагается по соглашению, чтобы исключить тривиальное кольцо , состоящее из одного элемента; это определяет любой выбор аксиом, определяющих поля.

Каждая конечная подгруппа мультипликативной группы поля является циклической (см. Корень из единицы § Циклические группы ).

Характеристика

В дополнение к умножению двух элементов F , можно определить произведение n ⋅ a произвольного элемента a из F на положительное целое число n как n -кратную сумму

a + a + ... + a (который является элементом F .)

Если не существует такого положительного целого числа, что

н ⋅ 1 = 0 ,

тогда говорят, что F имеет характеристику 0. [ 11 ^] Например, поле рациональных чисел Q имеет характеристику 0, поскольку никакое положительное целое число n не равно нулю. В противном случае, если существует положительное целое число n, удовлетворяющее этому уравнению, можно показать, что наименьшее такое положительное целое число является простым числом . Обычно оно обозначается как p , и говорят, что поле имеет характеристику p тогда. Например, поле F ₄ имеет характеристику 2 , поскольку (в обозначениях приведенной выше таблицы сложения) I + I = O.

Если F имеет характеристику p , то p ⋅ a = 0 для всех a из F. Это означает, что

( а + б ) ^р = а ^р + б ^р ,

так как все остальные биномиальные коэффициенты , входящие в биномиальную формулу, делятся на p . Здесь a ^p  := a ⋅ a ⋅ ⋯ ⋅ a ( p factors) — это p -я степень, т. е. p -кратное произведение элемента a . Следовательно, отображение Фробениуса

Ф → Ф  : х ↦ х ^п

совместимо со сложением в F (а также с умножением) и, следовательно, является гомоморфизмом поля. ^[12] Существование этого гомоморфизма делает поля в характеристике p совершенно отличными от полей характеристики 0 .

Подполя и основные поля

Подполе E поля F — это подмножество F , которое является полем относительно полевых операций F. Эквивалентно E — это подмножество F , которое содержит 1 и замкнуто относительно сложения, умножения, аддитивного обратного и мультипликативного обратного ненулевого элемента. Это означает, что 1 ∊ E , что для всех a , b ∊ E и a + b , и a ⋅ b принадлежат E , и что для всех a ≠ 0 в E , и − a, и 1 / a принадлежат E.

Гомоморфизмы полей — это отображения φ : E → F между двумя полями, такие, что φ ( e ₁ + e ₂ ) = φ ( e ₁ ) + φ ( e ₂ ) , φ ( e ₁ e ₂ ) = φ ( e ₁ )  φ ( e ₂ ) и φ (1 _E ) = 1 _F , где e ₁ и e ₂ — произвольные элементы E . Все гомоморфизмы полей инъективны . ^[13] Если φ также сюръективно , это называется изоморфизмом (или поля E и F называются изоморфными).

Поле называется простым полем, если оно не имеет собственных (т.е. строго меньших) подполей. Любое поле F содержит простое поле. Если характеристика F равна p (простое число), простое поле изоморфно конечному полю F _{p ,} введенному ниже. В противном случае простое поле изоморфно Q . ^[14]

Конечные поля

Конечные поля (также называемые полями Галуа ) — это поля с конечным числом элементов, число которых также называется порядком поля. Приведенный выше вводный пример F ₄ — это поле с четырьмя элементами. Его подполе F ₂ — это наименьшее поле, поскольку по определению поле имеет по крайней мере два различных элемента, 0 и 1 .

В модульной арифметике по модулю 12, 9 + 4 = 1, так как 9 + 4 = 13 в Z , что при делении на 12 дает остаток  1. Однако Z /12 Z не является полем, поскольку 12 не является простым числом.

Простейшие конечные поля с простым порядком наиболее доступны напрямую с помощью модульной арифметики . Для фиксированного положительного целого числа n арифметика "по модулю n " означает работу с числами

Z / n Z = {0, 1, ..., n − 1}.

Сложение и умножение на этом множестве выполняются путем выполнения рассматриваемой операции в множестве целых чисел Z , деления на n и взятия остатка в качестве результата. Эта конструкция дает поле точно, если n является простым числом . Например, взятие простого числа n = 2 приводит к вышеупомянутому полю F ₂ . Для n = 4 и, в более общем случае, для любого составного числа (т. е. любого числа n , которое может быть выражено как произведение n = r ⋅ s двух строго меньших натуральных чисел), Z / n Z не является полем: произведение двух ненулевых элементов равно нулю, поскольку r ⋅ s = 0 в Z / n Z , что, как было объяснено выше, не позволяет Z / n Z быть полем. Поле Z / p Z с p элементами ( p является простым числом), построенное таким образом, обычно обозначается как F _p .

Каждое конечное поле F имеет q = p ⁿ элементов, где p — простое число, а n ≥ 1. Это утверждение справедливо, поскольку F можно рассматривать как векторное пространство над его простым полем. Размерность этого векторного пространства обязательно конечна, скажем, n , что подразумевает утверждаемое утверждение. ^[15]

Поле с q = p ⁿ элементами может быть построено как поле разбиения многочлена

f ( x ) = x ^q − x .

Такое поле расщепления является расширением F _{p ,} в котором многочлен f имеет q нулей. Это означает, что f имеет столько нулей, сколько возможно, поскольку степень f равна q . Для q = 2 ² = 4 можно проверить в каждом конкретном случае с помощью приведенной выше таблицы умножения, что все четыре элемента F 4 удовлетворяют уравнению x ⁴ = x , поэтому они являются нулями f . Напротив, в F ₂ f имеет только два нуля (а именно 0 и 1 ), поэтому f не распадается на линейные множители в этом меньшем поле. Развивая далее основные понятия теории поля , можно показать _, что два конечных поля с одинаковым порядком изоморфны. ^[16] Таким образом, принято говорить о конечном поле с q элементами, обозначаемом F _q или GF( q ) .

История

Исторически три алгебраические дисциплины привели к понятию поля: вопрос решения полиномиальных уравнений, алгебраическая теория чисел и алгебраическая геометрия . ^[17] Первый шаг к понятию поля был сделан в 1770 году Жозефом -Луи Лагранжем , который заметил, что перестановка нулей x ₁ , x ₂ , x ₃ кубического многочлена в выражении

( х ₁ + ωx ₂ + ω ² х ₃ ) ³

(где ω — третий корень из единицы ) дает только два значения. Таким образом, Лагранж концептуально объяснил классический метод решения Сципиона дель Ферро и Франсуа Виэта , который осуществляется путем сведения кубического уравнения для неизвестного x к квадратному уравнению для x ³ . ^[18] Вместе с аналогичным наблюдением для уравнений степени 4 , Лагранж таким образом связал то, что в конечном итоге стало концепцией полей, и концепцией групп. ^[19] Вандермонд , также в 1770 году, и в более полной степени Карл Фридрих Гаусс , в своих Disquisitiones Arithmeticae (1801) изучали уравнение

х ^р = 1

для простого числа p и, снова используя современный язык, полученную циклическую группу Галуа . Гаусс вывел, что правильный p -угольник может быть построен, если p = 2 ^{2 k} + 1 . Основываясь на работе Лагранжа, Паоло Руффини утверждал (1799), что уравнения пятой степени (полиномиальные уравнения степени 5 ) не могут быть решены алгебраически; однако его аргументы были ошибочными. Эти пробелы были заполнены Нильсом Хенриком Абелем в 1824 году. ^[20] Эварист Галуа в 1832 году разработал необходимые и достаточные критерии для того, чтобы полиномиальное уравнение было алгебраически разрешимым, тем самым фактически установив то, что сегодня известно как теория Галуа . И Абель, и Галуа работали с тем, что сегодня называется алгебраическим числовым полем , но не придумали ни явного понятия поля, ни группы.

В 1871 году Ричард Дедекинд ввел для набора действительных или комплексных чисел, который замкнут относительно четырех арифметических операций, немецкое слово Körper , что означает «тело» или «корпус» (чтобы обозначить органически замкнутую сущность). Английский термин «поле» был введен Муром (1893). ^[21]

Под полем мы будем понимать каждую бесконечную систему действительных или комплексных чисел, настолько замкнутую в себе и совершенную, что сложение, вычитание, умножение и деление любых двух из этих чисел снова дает число этой системы.

-  Ричард Дедекинд, 1871 г. ^[22]

В 1881 году Леопольд Кронекер определил то, что он назвал областью рациональности , которая является полем рациональных дробей в современных терминах. Понятие Кронекера не охватывало поле всех алгебраических чисел (которое является полем в смысле Дедекинда), но с другой стороны было более абстрактным, чем у Дедекинда, в том смысле, что оно не делало никаких конкретных предположений о природе элементов поля. Кронекер интерпретировал поле, такое как Q (π), абстрактно как поле рациональных функций Q ( X ) . До этого примеры трансцендентных чисел были известны со времен работы Жозефа Лиувилля в 1844 году, пока Шарль Эрмит (1873) и Фердинанд фон Линдеманн (1882) не доказали трансцендентность e и π соответственно. ^[23]

Первое четкое определение абстрактного поля принадлежит Веберу (1893). ^[24] В частности, понятие Генриха Мартина Вебера включало поле F _p . Джузеппе Веронезе (1891) изучал поле формальных степенных рядов, что привело Гензеля (1904) к введению поля p -адических чисел. Штейниц (1910) синтезировал знания абстрактной теории поля, накопленные к настоящему времени. Он аксиоматически изучал свойства полей и определил многие важные концепции теории поля. Большинство теорем, упомянутых в разделах Теория Галуа, Построение полей и Элементарные понятия, можно найти в работе Штейница. Артин и Шрайер (1927) связали понятие упорядоченности в поле и, таким образом, область анализа с чисто алгебраическими свойствами. ^[25] Эмиль Артин переработал теорию Галуа с 1928 по 1942 год, устранив зависимость от теоремы о примитивном элементе .

Построение полей

Построение полей из колец

Коммутативное кольцо — это множество, которое снабжено операциями сложения и умножения и удовлетворяет всем аксиомам поля, за исключением существования мультипликативных обратных чисел a ⁻¹ . ^[26] Например, целые числа Z образуют коммутативное кольцо, но не поле: обратная величина целого числа n сама по себе не является целым числом, если только n = ±1 .

В иерархии алгебраических структур поля можно охарактеризовать как коммутативные кольца R , в которых каждый ненулевой элемент является единицей (что означает, что каждый элемент обратим). Аналогично, поля являются коммутативными кольцами с ровно двумя различными идеалами , (0) и R. Поля также являются в точности коммутативными кольцами, в которых (0) является единственным простым идеалом .

Если задано коммутативное кольцо R , то существует два способа построить поле, связанное с R , т. е. два способа модификации R таким образом, чтобы все ненулевые элементы стали обратимыми: формирование поля дробей и формирование полей вычетов. Поле дробей Z — это Q , рациональные числа, тогда как поля вычетов Z — это конечные поля F _p .

Поле дробей

Если задана область целостности R , ее поле дробей Q ( R ) строится из дробей двух элементов R точно так же, как Q строится из целых чисел. Точнее, элементы Q ( R ) — это дроби a / b , где a и b находятся в R , а b ≠ 0 . Две дроби a / b и c / d равны тогда и только тогда, когда ad = bc . Операция над дробями работает точно так же, как для рациональных чисел. Например,

${\displaystyle {\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}.}$

Легко показать, что если кольцо является целостной областью, то множество дробей образует поле. ^[27]

Поле F ( x ) рациональных дробей над полем (или областью целостности) F есть поле дробей кольца многочленов F [ x ] . Поле F (( x )) рядов Лорана

${\displaystyle \sum _{i=k}^{\infty }a_{i}x^{i}\ (k\in \mathbb {Z} ,a_{i}\in F)}$

над полем F есть поле дробей кольца F [[ x ]] формальных степенных рядов (в котором k ≥ 0 ). Поскольку любой ряд Лорана является дробью степенного ряда, деленной на степень x (в отличие от произвольного степенного ряда), то представление дробей в этой ситуации, однако, менее важно.

Поля остатков

В дополнение к полю дробей, которое инъективно вкладывает R в поле, поле может быть получено из коммутативного кольца R с помощью сюръективного отображения на поле F. Любое поле, полученное таким образом, является фактором R / m , где m — максимальный идеал R. Если R имеет только один максимальный идеал m , это поле называется полем вычетов R. [ ²⁸ ]

Идеал , порождённый одним многочленом f в кольце многочленов R = E [ X ] (над полем E ), максимален тогда и только тогда, когда f неприводим в E , т. е. если f не может быть выражен как произведение двух многочленов в E [ X ] меньшей степени . Это даёт поле

F = E [ X ] / ( f ( X )).

Это поле F содержит элемент x (а именно класс остатков X ) , который удовлетворяет уравнению

f ( x ) = 0.

Например, C получается из R присоединением символа мнимой единицы i , что удовлетворяет f ( i ) = 0 , где f ( X ) = X ² + 1. Более того, f неприводим над R , что подразумевает , что отображение , которое переводит многочлен f ( X ) ∊ R [ X ] в f ( i ), дает изоморфизм

${\displaystyle \mathbf {R} [X]/\left(X^{2}+1\right)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbf {C} .}$

Создание полей внутри большего поля

Поля могут быть построены внутри заданного большего контейнерного поля. Предположим, что задано поле E и поле F , содержащее E как подполе. Для любого элемента x из F существует наименьшее подполе F , содержащее E и x , называемое подполем F, порожденным x, и обозначаемое E ( x ) . ^[29] Переход от E к E ( x ) обозначается присоединением элемента к E . В более общем смысле, для подмножества S ⊂ F существует минимальное подполе F , содержащее E и S , обозначаемое E ( S ) .

Композитум двух подполей E и E ′ некоторого поля F — это наименьшее подполе F , содержащее как E, так и E ′ . Композитум можно использовать для построения наибольшего подполя F, удовлетворяющего определенному свойству, например, наибольшего подполя F , которое на языке, введенном ниже, является алгебраическим над E . ^[c]

Расширения поля

Понятие подполя E ⊂ F можно также рассматривать с противоположной точки зрения, ссылаясь на F как на расширение поля (или просто расширение) E , обозначаемое как

Ф / Э ,

и прочитайте « F над E ».

Базисным параметром расширения поля является его степень [ F  : E ] , т. е. размерность F как E -векторного пространства. Она удовлетворяет формуле ^[30]

[ Г  : Э ] = [ Г  : Ж ] [ Ж  : Э ] .

_{Расширения , степень} которых конечна, называются конечными расширениями. Расширения C / R и F4 / F2 имеют степень 2 , тогда как R / Q является бесконечным расширением.

Алгебраические расширения

Ключевым понятием в изучении расширений полей F / E являются алгебраические элементы . Элемент x ∈ F является алгебраическим над E, если он является корнем многочлена с коэффициентами в E , то есть если он удовлетворяет полиномиальному уравнению

ен х ⁿ + ен ₋₁ х ⁿ ₋₁ ⁺ _⋯  + е ₁ х + е ₀ = 0 ,

с e _n , ..., e ₀ в E , и e _n ≠ 0 . Например, мнимая единица i в C является алгебраической над R , и даже над Q , так как она удовлетворяет уравнению

я ² + 1 = 0 .

Расширение поля, в котором каждый элемент F является алгебраическим над E , называется алгебраическим расширением . Любое конечное расширение обязательно является алгебраическим, как можно вывести из приведенной выше формулы мультипликативности. ^[31]

Подполе E ( x ), порожденное элементом x , как указано выше, является алгебраическим расширением E тогда и только тогда, когда x является алгебраическим элементом. То есть, если x является алгебраическим, все остальные элементы E ( x ) обязательно также являются алгебраическими. Более того, степень расширения E ( x ) / E , т. е. размерность E ( x ) как E -векторного пространства, равна минимальной степени n такой, что существует полиномиальное уравнение, включающее x , как указано выше. Если эта степень равна n , то элементы E ( x ) имеют вид

${\displaystyle \sum _{k=0}^{n-1}a_{k}x^{k},\ \ a_{k}\in E.}$

Например, поле Q ( i ) гауссовых рациональных чисел является подполем C, состоящим из всех чисел вида a + bi , где и a, и b являются рациональными числами: слагаемые вида i ² (и аналогично для более высоких показателей) здесь не обязательно должны рассматриваться, поскольку a + bi + ci ² можно упростить до a − c + bi .

Основы трансцендентности

Вышеупомянутое поле рациональных дробей E ( X ) , где X — неопределённость , не является алгебраическим расширением E , поскольку не существует полиномиального уравнения с коэффициентами в E , нулем которого является X . Элементы, такие как X , которые не являются алгебраическими, называются трансцендентными . Неформально говоря, неопределённость X и её степени не взаимодействуют с элементами E . Аналогичное построение можно осуществить с набором неопределённостей, а не только с одной.

Опять же, расширение поля E ( x ) / E , обсуждавшееся выше, является ключевым примером: если x не является алгебраическим (т. е. x не является корнем многочлена с коэффициентами в E ), то E ( x ) изоморфно E ( X ) . Этот изоморфизм получается путем подстановки x в X в рациональных дробях.

Подмножество S поля F является базисом трансцендентности , если оно алгебраически независимо (не удовлетворяет никаким полиномиальным соотношениям) над E и если F является алгебраическим расширением E ( S ) . Любое расширение поля F / E имеет базис трансцендентности. ^[32] Таким образом, расширения полей можно разбить на расширения вида E ( S ) / E ( чисто трансцендентные расширения ) и алгебраические расширения.

Закрытие операций

Поле алгебраически замкнуто , если оно не имеет строго больших алгебраических расширений или, что эквивалентно, если любое полиномиальное уравнение

f _n  x ⁿ + f _{n −1} x ^{n −1} + ⋯ + f ₁ x + f ₀ = 0 , с коэффициентами f _n , ..., f ₀ ∈ F , n > 0 ,

имеет решение x ∊ F . ^[33] По основной теореме алгебры , C алгебраически замкнуто, т.е. любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение. Рациональные и действительные числа не являются алгебраически замкнутыми, так как уравнение

х ² + 1 = 0

не имеет рационального или действительного решения. Поле, содержащее F, называется алгебраическим замыканием F , если оно алгебраично над F (грубо говоря, не слишком велико по сравнению с F ) и алгебраически замкнуто (достаточно велико, чтобы содержать решения всех полиномиальных уравнений).

Согласно вышесказанному, C является алгебраическим замыканием поля R. Ситуация, когда алгебраическое замыкание является конечным расширением поля F, является весьма частной: по теореме Артина–Шрайера степень этого расширения обязательно равна 2 , и F элементарно эквивалентно R. Такие поля также известны как действительные замкнутые поля .

Любое поле F имеет алгебраическое замыкание, которое, более того, единственно с точностью до (неединственного) изоморфизма. Его обычно называют алгебраическим замыканием и обозначают F . Например, алгебраическое замыкание Q поля Q называется полем алгебраических чисел . Поле F обычно довольно неявно, поскольку его построение требует леммы об ультрафильтре , теоретико-множественной аксиомы, которая слабее аксиомы выбора . ^[34] В этом отношении алгебраическое замыкание поля F _q , исключительно просто. Оно представляет собой объединение конечных полей, содержащих F _q (порядка q ⁿ ). Для любого алгебраически замкнутого поля F характеристики 0 алгебраическое замыкание поля F (( t )) рядов Лорана является полем рядов Пюизе , полученных присоединением корней t . ^[35]

Поля с дополнительной структурой

Поскольку поля повсеместно присутствуют в математике и за ее пределами, несколько уточнений этой концепции были адаптированы к потребностям конкретных областей математики.

Упорядоченные поля

Поле F называется упорядоченным полем , если любые два элемента можно сравнить, так что x + y ≥ 0 и xy ≥ 0 всякий раз, когда x ≥ 0 и y ≥ 0 . Например, действительные числа образуют упорядоченное поле с обычным порядком  ≥ . Теорема Артина–Шрайера утверждает, что поле может быть упорядочено тогда и только тогда, когда оно является формально действительным полем , что означает, что любое квадратное уравнение

${\displaystyle x_{1}^{2}+x_{2}^{2}+\dots +x_{n}^{2}=0}$

имеет только решение x ₁ = x ₂ = ⋯ = x _n = 0 . ^[36] Множество всех возможных порядков на фиксированном поле F изоморфно множеству кольцевых гомоморфизмов из кольца Витта W( F ) квадратичных форм над F в Z . ^[37]

Архимедово поле — это упорядоченное поле, для каждого элемента которого существует конечное выражение

1 + 1 + ⋯ + 1

чье значение больше этого элемента, то есть нет бесконечных элементов. Эквивалентно, поле не содержит бесконечно малых (элементов, меньших всех рациональных чисел); или, что еще эквивалентно, поле изоморфно подполю R .

Каждое ограниченное действительное множество имеет наименьшую верхнюю границу.

Упорядоченное поле является дедекиндово-полным, если все верхние границы , нижние границы (см. разрез Дедекинда ) и пределы, которые должны существовать, существуют. Более формально, каждое ограниченное подмножество F должно иметь наименьшую верхнюю границу. Любое полное поле обязательно архимедово, ^[38] поскольку в любом неархимедовом поле нет ни наибольшего бесконечно малого, ни наименьшего положительного рационального числа, откуда последовательность 1/2 , 1/3, 1/4, ... , каждый элемент которой больше любого бесконечно малого, не имеет предела.

Поскольку каждое собственное подполе действительных чисел также содержит такие пробелы, R является единственным полным упорядоченным полем с точностью до изоморфизма. ^[39] Несколько основополагающих результатов в исчислении непосредственно следуют из этой характеристики действительных чисел.

Гиперреальные числа R ^* образуют упорядоченное поле, которое не является архимедовым. Это расширение действительных чисел, полученное включением бесконечных и бесконечно малых чисел. Они больше, соответственно меньше любого действительного числа. Гиперреальные числа образуют фундаментальную основу нестандартного анализа .

Топологические поля

Другим уточнением понятия поля является топологическое поле , в котором множество F является топологическим пространством , таким, что все операции поля (сложение, умножение, отображения a ↦ − a и a ↦ a ⁻¹ ) являются непрерывными отображениями относительно топологии пространства. ^[40] Топология всех полей, обсуждаемых ниже, индуцируется из метрики , т. е . функции

г  : Ф × Ф → Р ,

который измеряет расстояние между любыми двумя элементами F.

Завершение F — это еще одно поле, в котором, неформально говоря, заполняются «пробелы» в исходном поле F , если таковые имеются. Например, любое иррациональное число x , такое как x = √ 2 , является «пробелом» в рациональных числах Q в том смысле , что это действительное число, которое может быть сколь угодно близко аппроксимировано рациональными числами p / q , в том смысле, что расстояние между x и p / q, заданное абсолютным значением | x − p / q |, сколь угодно мало. В следующей таблице перечислены некоторые примеры такой конструкции. В четвертом столбце показан пример нулевой последовательности , т. е. последовательности, предел которой (при n → ∞ ) равен нулю.

Поле Q _p используется в теории чисел и p -адическом анализе . Алгебраическое замыкание Q _p несет уникальную норму, расширяющую норму на Q _p , но не является полным. Завершение этого алгебраического замыкания, однако, алгебраически замкнуто. Из-за его грубой аналогии с комплексными числами его иногда называют полем комплексных p -адических чисел и обозначают C _p . ^[41]

Местные поля

Следующие топологические поля называются локальными полями : ^{[42] [d]}

• конечные расширения Q _p (локальные поля нулевой характеристики)
• конечные расширения F _p (( t )) , поля рядов Лорана над F _p (локальные поля характеристики p ).

Эти два типа локальных полей имеют некоторые фундаментальные сходства. В этом отношении элементы p ∈ Q _p и t ∈ F _p (( t )) (называемые униформизатором ) соответствуют друг другу. Первое проявление этого происходит на элементарном уровне: элементы обоих полей могут быть выражены как степенные ряды в униформизаторе с коэффициентами в F _p . (Однако, поскольку сложение в Q _p выполняется с использованием переноса , чего нет в F _p (( t )) , эти поля не изоморфны.) Следующие факты показывают, что это поверхностное сходство идет гораздо глубже:

• Любое утверждение первого порядка , которое верно для почти всех Q _{p ,} верно также и для почти всех F _p (( t )) . Приложением этого является теорема Акса–Кохена, описывающая нули однородных многочленов в Q _p .
• Слабо разветвленные расширения обоих полей находятся во взаимной однозначности друг с другом.
• Присоединение произвольных корней p -степени p (в Q _p ), соответственно t (в F _p (( t )) ), дает (бесконечные) расширения этих полей, известные как перфектоидные поля . Поразительно, что группы Галуа этих двух полей изоморфны, что является первым проблеском замечательной параллели между этими двумя полями: ^[43] $${\displaystyle \operatorname {Gal} \left(\mathbf {Q} _{p}\left(p^{1/p^{\infty }}\right)\right)\cong \operatorname {Gal} \left(\mathbf {F} _{p}((t))\left(t^{1/p^{\infty }}\right)\right).}$$

Дифференциальные поля

Дифференциальные поля — это поля, снабженные деривацией , т. е. позволяющие брать производные элементов в поле. ^[44] Например, поле R ( X ) вместе со стандартной производной полиномов образует дифференциальное поле. Эти поля являются центральными в дифференциальной теории Галуа , варианте теории Галуа, имеющем дело с линейными дифференциальными уравнениями .

теория Галуа

Теория Галуа изучает алгебраические расширения поля, изучая симметрию в арифметических операциях сложения и умножения. Важным понятием в этой области является понятие конечных расширений Галуа F / E , которые по определению являются теми, которые являются отделимыми и нормальными . Теорема о примитивном элементе показывает, что конечные отделимые расширения обязательно являются простыми , т. е. имеют вид

F = E [ X ] / f ( X ) ,

где f — неприводимый многочлен (как и выше). ^[45] Для такого расширения быть нормальным и отделимым означает, что все нули f содержатся в F и что f имеет только простые нули. Последнее условие всегда выполняется, если E имеет характеристику 0 .

Для конечного расширения Галуа группа Галуа Gal( F / E ) является группой автоморфизмов полей F , которые тривиальны на E (т. е. биекции σ  : F → F , которые сохраняют сложение и умножение и которые отправляют элементы E в себя). Важность этой группы вытекает из фундаментальной теоремы теории Галуа , которая строит явное взаимно-однозначное соответствие между множеством подгрупп Gal ( F / E ) и множеством промежуточных расширений расширения F / E . ^[46] С помощью этого соответствия теоретико-групповые свойства переводятся в факты о полях. Например, если группа Галуа расширения Галуа, как указано выше, неразрешима ( не может быть построена из абелевых групп ), то нули f не могут быть выражены в терминах сложения, умножения и радикалов, т. е. выражений, включающих . Например, симметрическая группа S _n неразрешима для n ≥ 5 . Следовательно, как можно показать, нули следующих многочленов не выражаются через суммы, произведения и радикалы. Для последнего многочлена этот факт известен как теорема Абеля–Руффини : ${\displaystyle {\sqrt[{n}]{~}}}$

f ( X ) = X ⁵ − 4 X + 2 (и E = Q ), ^[47]

f ( X ) = X ⁿ + a _{n −1} X ^{n −1} + ⋯ + a ₀ (где f рассматривается как многочлен от E ( a ₀ , ..., an ₋₁ ) для некоторых неизвестных a _i , E — любое поле, и _n ≥ 5 ) .

Тензорное произведение полей обычно не является полем. Например, конечное расширение F / E степени n является расширением Галуа тогда и только тогда, когда существует изоморфизм F -алгебр

F ⊗ _E F ≅ F ⁿ .

Этот факт является началом теории Галуа Гротендика , далеко идущего расширения теории Галуа, применимой к алгебро-геометрическим объектам. ^[48]

Инварианты полей

Базовые инварианты поля F включают характеристику и степень трансцендентности F над его простым полем. Последняя определяется как максимальное число элементов в F , которые алгебраически независимы над простым полем. Два алгебраически замкнутых поля E и F изоморфны в точности, если эти два данных совпадают. ^[49] Это означает, что любые два несчетных алгебраически замкнутых поля одинаковой мощности и одинаковой характеристики изоморфны. Например, Q _p , C _p и C изоморфны (но не изоморфны как топологические поля).

Модельная теория полей

В теории моделей , разделе математической логики , два поля E и F называются элементарно эквивалентными , если каждое математическое утверждение, которое верно для E, также верно для F и наоборот. Математические утверждения, о которых идет речь, должны быть предложениями первого порядка (включая 0 , 1 , сложение и умножение). Типичным примером для n > 0 , n — целое число, является

φ ( E ) = "любой многочлен степени n в E имеет ноль в E "

Набор таких формул для всех n выражает, что E алгебраически замкнуто. Принцип Лефшеца утверждает, что C элементарно эквивалентно любому алгебраически замкнутому полю F нулевой характеристики. Более того, любое фиксированное утверждение φ выполняется в C тогда и только тогда, когда оно выполняется в любом алгебраически замкнутом поле достаточно высокой характеристики. ^[50]

Если U — ультрафильтр на множестве I , а F _i — поле для каждого i из I , то ультрапроизведение F i относительно _U является полем . ^[51] Оно обозначается как

ulim _{i →∞} F _i ,

поскольку он ведет себя несколькими способами как предел полей F _i : теорема Лоса утверждает, что любое утверждение первого порядка, которое справедливо для всех, кроме конечного числа F _i , справедливо также и для ультрапроизведения. Применительно к приведенному выше предложению φ это показывает, что существует изоморфизм ^[e]

${\displaystyle \operatorname {ulim} _{p\to \infty }{\overline {\mathbf {F} }}_{p}\cong \mathbf {C} .}$

Упомянутая выше теорема Акса–Кохена также следует из этого и изоморфизма ультрапроизведений (в обоих случаях по всем простым числам p )

ulim _p Q _p ≅ ulim _p F _p (( t )) .

Кроме того, теория моделей также изучает логические свойства различных других типов полей, таких как действительные замкнутые поля или экспоненциальные поля (которые снабжены экспоненциальной функцией exp : F → F ^× ). ^[52]

Абсолютная группа Галуа

Для полей, которые не являются алгебраически замкнутыми (или не являются сепарабельно замкнутыми), абсолютная группа Галуа Gal( F ) имеет принципиально важное значение: расширяя случай конечных расширений Галуа, описанных выше, эта группа управляет всеми конечными сепарабельными расширениями F . Элементарными средствами можно показать, что группа Gal( F q ) является группой Прюфера, проконечным пополнением Z . Это утверждение включает тот факт _, что единственными алгебраическими расширениями Gal ( F q ) _{являются} поля Gal ( F _{q ⁿ} ) для n > 0 , и что группы Галуа этих конечных расширений задаются как

Гал( F _{q ⁿ} / F _q ) = Z / n Z .

Описание в терминах генераторов и соотношений известно также для групп Галуа полей p -адических чисел (конечных расширений Q _p ). ^[53]

Представления групп Галуа и связанных с ними групп, таких как группа Вейля, являются фундаментальными во многих разделах арифметики, таких как программа Ленглендса . Когомологическое исследование таких представлений выполняется с использованием когомологий Галуа . ^[54] Например, группа Брауэра , которая классически определяется как группа центральных простых F -алгебр , может быть переинтерпретирована как группа когомологий Галуа, а именно

Br( F ) = H ² ( F , G _m ) .

К-теория

К-теория Милнора определяется как

${\displaystyle K_{n}^{M}(F)=F^{\times }\otimes \cdots \otimes F^{\times }/\left\langle x\otimes (1-x)\mid x\in F\smallsetminus \{0,1\}\right\rangle .}$

Теорема об изоморфизме норменного вычета , доказанная около 2000 года Владимиром Воеводским , связывает это с когомологиями Галуа посредством изоморфизма

${\displaystyle K_{n}^{M}(F)/p=H^{n}(F,\mu _{l}^{\otimes n}).}$

Алгебраическая K-теория связана с группой обратимых матриц с коэффициентами в заданном поле. Например, процесс взятия определителя обратимой матрицы приводит к изоморфизму K ₁ ( F ) = F ^× . Теорема Мацумото показывает, что K ₂ ( F ) согласуется с K ₂ ^M ( F ) . В более высоких степенях K-теория расходится с K-теорией Милнора и остается трудновычислимой в общем случае.

Приложения

Линейная алгебра и коммутативная алгебра

Если a ≠ 0 , то уравнение

ах = б

имеет единственное решение x в поле F , а именно Это непосредственное следствие определения поля является фундаментальным в линейной алгебре . Например, это существенный ингредиент гауссовского исключения и доказательства того, что любое векторное пространство имеет базис . ^[55] ${\displaystyle x=a^{-1}b.}$

Теория модулей (аналог векторных пространств над кольцами вместо полей) гораздо сложнее, поскольку приведенное выше уравнение может иметь несколько решений или не иметь ни одного. В частности, системы линейных уравнений над кольцом гораздо сложнее решить, чем в случае полей, даже в особенно простом случае кольца Z целых чисел.

Конечные поля: криптография и теория кодирования

Сумма трех точек P , Q и R на эллиптической кривой E (красной) равна нулю, если через эти точки проходит прямая (синяя).

Широко применяемая криптографическая процедура использует тот факт, что дискретное возведение в степень, т. е. вычисление

a ⁿ = a ⋅ a ⋅ ⋯ ⋅ a ( n множителей, для целого числа n ≥ 1 )

в (большом) конечном поле F _q может быть выполнено гораздо эффективнее, чем дискретное логарифмирование , которое является обратной операцией, т.е. определением решения n уравнения

а ^н = б .

В криптографии эллиптических кривых умножение в конечном поле заменяется операцией сложения точек на эллиптической кривой , т. е. решений уравнения вида

у2 = х3 + ах + Ь .^​​

Конечные поля также используются в теории кодирования и комбинаторике .

Геометрия: поле функций

Компактная риманова поверхность рода два (две ручки). Род можно считать из поля мероморфных функций на поверхности.

Функции на подходящем топологическом пространстве X в поле F можно складывать и умножать поточечно, например, произведение двух функций определяется произведением их значений в области определения:

( f ⋅ g )( x ) = f ( x ) ⋅ g ( x ) .

Это делает эти функции F - коммутативной алгеброй .

Для того, чтобы иметь поле функций, нужно рассмотреть алгебры функций, которые являются областями целостности . В этом случае отношения двух функций, т.е. выражения вида

${\displaystyle {\frac {f(x)}{g(x)}},}$

образуют поле, называемое полем функций.

Это происходит в двух основных случаях. Когда X — комплексное многообразие X . В этом случае рассматривается алгебра голоморфных функций , т.е. комплексных дифференцируемых функций. Их отношения образуют поле мероморфных функций на X .

Поле функций алгебраического многообразия X (геометрический объект, определяемый как общие нули полиномиальных уравнений) состоит из отношений регулярных функций , т. е. отношений полиномиальных функций на многообразии. Поле функций n -мерного пространства над полем F есть F ( x ₁ , ..., x _n ) , т. е. поле, состоящее из отношений полиномов от n неизвестных. Поле функций X такое же, как и поле любого открытого плотного подмногообразия. Другими словами, поле функций нечувствительно к замене X на (немного) меньшее подмногообразие.

Поле функций инвариантно относительно изоморфизма и бирациональной эквивалентности многообразий. Поэтому оно является важным инструментом для изучения абстрактных алгебраических многообразий и для классификации алгебраических многообразий. Например, размерность , которая равна степени трансцендентности F ( X ) , инвариантна относительно бирациональной эквивалентности. ^[56] Для кривых (т. е. размерность равна единице) поле функций F ( X ) очень близко к X : если X является гладким и собственным (аналог компактности ) , X может быть восстановлено с точностью до изоморфизма из его поля функций. ^[f] В более высокой размерности поле функций помнит меньше, но все еще решающую информацию о X . Изучение полей функций и их геометрического смысла в более высоких размерностях называется бирациональной геометрией . Программа минимальной модели пытается идентифицировать простейшие (в определенном точном смысле) алгебраические многообразия с предписанным полем функций.

Теория чисел: глобальные поля

Глобальные поля находятся в центре внимания в алгебраической теории чисел и арифметической геометрии . Они, по определению, являются числовыми полями (конечными расширениями Q ) или функциональными полями над F _q (конечными расширениями F _q ( t ) ). Что касается локальных полей, эти два типа полей имеют несколько схожих черт, хотя они имеют характеристику 0 и положительную характеристику соответственно. Эта аналогия с функциональным полем может помочь сформировать математические ожидания, часто сначала путем понимания вопросов о функциональных полях, а затем рассмотрения случая числового поля. Последнее часто бывает сложнее. Например, гипотезу Римана относительно нулей дзета-функции Римана (открытую в 2017 году) можно рассматривать как параллельную гипотезам Вейля (доказанным в 1974 году Пьером Делинем ).

Пятые корни из единицы образуют правильный пятиугольник .

Циклотомические поля являются одними из наиболее интенсивно изучаемых числовых полей. Они имеют вид Q ( ζ _n ) , где ζ _n — примитивный корень n-й степени из единицы , т. е. комплексное число ζ , которое удовлетворяет ζ ⁿ = 1 и ζ ^m ≠ 1 для всех 0 < m < n . ^[57] Для n , являющегося обычным простым числом , Куммер использовал циклотомические поля для доказательства Великой теоремы Ферма , которая утверждает несуществование рациональных ненулевых решений уравнения

хn + yn = zn .^​​​

Локальные поля являются пополнениями глобальных полей. Теорема Островского утверждает, что единственными пополнениями Q , глобального поля, являются локальные поля Q _p и R . Изучение арифметических вопросов в глобальных полях иногда может быть выполнено путем рассмотрения соответствующих вопросов локально. Этот метод называется локально-глобальным принципом . Например, теорема Хассе–Минковского сводит задачу поиска рациональных решений квадратных уравнений к решению этих уравнений в R и Q _p , решения которых можно легко описать. ^[58]

В отличие от локальных полей, группы Галуа глобальных полей неизвестны. Обратная теория Галуа изучает (нерешенную) проблему, является ли любая конечная группа группой Галуа Gal( F / Q ) для некоторого числового поля F . ^[59] Теория полей классов описывает абелевы расширения , т. е. расширения с абелевой группой Галуа или, что эквивалентно, абелианизированные группы Галуа глобальных полей. Классическое утверждение, теорема Кронекера–Вебера , описывает максимальное абелевое расширение Q ^{ab поля} Q : это поле

Q ( ζn _, n ≥ 2 )

полученный присоединением всех примитивных корней n-й степени из единицы. Югендтраум Кронекера требует аналогичного явного описания F ^ab общих числовых полей F . Для мнимых квадратичных полей , , d > 0 , теория комплексного умножения описывает F ^ab с помощью эллиптических кривых . Для общих числовых полей такое явное описание неизвестно. ${\displaystyle F=\mathbf {Q} ({\sqrt {-d}})}$

Связанные понятия

В дополнение к дополнительной структуре, которой могут обладать поля, поля допускают различные другие связанные понятия. Поскольку в любом поле 0 ≠ 1 , любое поле имеет по крайней мере два элемента. Тем не менее, существует концепция поля с одним элементом , которая, как предполагается, является пределом конечных полей F _p , когда p стремится к 1 . ^[60] В дополнение к кольцам деления существуют различные другие более слабые алгебраические структуры, связанные с полями, такие как квазиполя , почти-поля и полуполя .

Существуют также правильные классы с полевой структурой, которые иногда называют Полем s, с заглавной буквы «F». Сюрреалистические числа образуют Поле, содержащее действительные числа, и были бы полем, если бы не тот факт, что они являются правильным классом, а не множеством. Нимберы , концепция из теории игр , также образуют такое Поле. ^[61]

Кольца деления

Отбрасывание одной или нескольких аксиом в определении поля приводит к другим алгебраическим структурам. Как было упомянуто выше, коммутативные кольца удовлетворяют всем аксиомам поля, за исключением существования мультипликативных обратных. Отбрасывание вместо этого коммутативности умножения приводит к концепции деления кольца или тела ; ^[g] иногда ассоциативность также ослабляется. Единственными делениями, которые являются конечномерными R -векторными пространствами, являются само R , C (которое является полем) и кватернионы H (в которых умножение некоммутативно). Этот результат известен как теорема Фробениуса . Октонионы O , для которых умножение не является ни коммутативным, ни ассоциативным, являются нормированной альтернативной алгеброй с делением, но не являются делением. Этот факт был доказан с использованием методов алгебраической топологии в 1958 году Мишелем Кервером , Раулем Боттом и Джоном Милнором . ^[62]

Малая теорема Веддерберна утверждает, что все конечные тела являются полями.

Примечания

1. Априорное двойное использование символа « − » для обозначения одной части константы и для аддитивных обратных величин оправдано этим последним условием.
2. Эквивалентно, поле — это алгебраическая структура ⟨ F , +, ⋅, −, ⁻¹ , 0, 1⟩ типа ⟨2, 2, 1, 1, 0, 0⟩ , такая, что 0 ⁻¹ не определено, ⟨ F , +, −, 0⟩ и являются абелевыми группами, а ⋅ дистрибутивна над + . ^[10] ${\displaystyle \left\langle F\smallsetminus \{0\},\cdot ,{}^{-1}\right\rangle }$
3. Другие примеры включают максимальное неразветвленное расширение или максимальное абелево расширение внутри F.
4. Некоторые авторы также считают поля R и C локальными полями. С другой стороны, эти два поля, также называемые архимедовыми локальными полями, имеют мало общего с локальными полями, рассматриваемыми здесь, до такой степени, что Касселс (1986, стр. vi) называет их «полностью аномальными».
5. Оба C и ulim _p F _p алгебраически замкнуты по теореме Лося. По той же причине они оба имеют нулевую характеристику. Наконец, они оба несчетны, так что они изоморфны.
6. Точнее, существует эквивалентность категорий между гладкими собственными алгебраическими кривыми над алгебраически замкнутым полем F и конечными расширениями полей F ( T ) .
7. Исторически деления иногда назывались полями, а поля назывались коммутативными полями .

Цитаты

1. Бичи и Блэр (2006), Определение 4.1.1, стр. 181
2. Фрейли (1976), стр. 10
3. Маккой (1968), стр. 16
4. Кларк (1984), Глава 3
5. Майнс, Ричман и Рюитенбург (1988), §II.2. См. также поле Гейтинга .
6. Бичи и Блэр (2006), стр. 120, гл. 3
7. Артин (1991), Глава 13.4
8. Lidl & Niederreiter (2008), пример 1.62.
9. Бичи и Блэр (2006), стр. 120, гл. 3
10. Уоллес (1998), Ч. 2
11. Адамсон (2007), §I.2, стр. 10
12. Эскофьер (2012), 14.4.2
13. Адамсон (2007), §I.3
14. Адамсон (2007), стр. 12
15. Лидл и Нидеррайтер (2008), Лемма 2.1, Теорема 2.2
16. Лидл и Нидеррайтер (2008), Теорема 1.2.5
17. Кляйнер (2007), стр. 63
18. Кирнан (1971), стр. 50
19. Бурбаки (1994), стр. 75–76
20. Корри (2004), стр. 24
21. «Самые ранние известные случаи использования некоторых слов математики (F)».
22. Дирихле (1871), стр. 42, перевод Клейнера (2007), стр. 66
23. Бурбаки (1994), стр. 81
24. Корри (2004), стр. 33. См. также Фрике и Вебер (1924).
25. Бурбаки (1994), стр. 92
26. Ланг (2002), §II.1
27. Артин (1991), §10.6
28. Эйзенбуд (1995), стр. 60
29. Якобсон (2009), стр. 213
30. Артин (1991), Теорема 13.3.4
31. Артин (1991), Следствие 13.3.6
32. Бурбаки (1988), Глава V, §14, № 2, Теорема 1
33. Артин (1991), §13.9
34. Банашевски (1992). Пост на Mathoverflow
35. Рибенбойм (1999), стр. 186, §7.1
36. Бурбаки (1988), Глава VI, §2.3, Следствие 1
37. Лоренц (2008), §22, Теорема 1
38. Престель (1984), Предложение 1.22
39. Престель (1984), Теорема 1.23
40. Уорнер (1989), Глава 14
41. Гувеа (1997), §5.7
42. Серр (1979)
43. Шольце (2014)
44. ван дер Пут и Сингер (2003), §1
45. Лэнг (2002), Теорема V.4.6
46. Ланг (2002), §VI.1
47. Ланг (2002), Пример VI.2.6
48. Борсо и Джанелидзе (2001). См. также фундаментальную группу Étale .
49. Гувеа (2012), Теорема 6.4.8
50. Маркер, Мессмер и Пиллэй (2006), Следствие 1.2
51. Схоутенс (2002), §2
52. Кульманн (2000)
53. Яннсен и Вингберг (1982)
54. Серр (2002)
55. Артин (1991), §3.3
56. Эйзенбуд (1995), §13, Теорема A
57. Вашингтон (1997)
58. Серр (1996), Глава IV
59. Серр (1992)
60. Титьки (1957)
61. Конвей (1976)
62. Баез (2002)

Ссылки

• Адамсон, ИТ (2007), Введение в теорию поля , Dover Publications, ISBN 978-0-486-46266-0
• Алленби, RBJT (1991), Кольца, поля и группы , Butterworth-Heinemann, ISBN 978-0-340-54440-2
• Артин, Майкл (1991), Алгебра , Прентис Холл , ISBN 978-0-13-004763-2, особенно Глава 13
• Артин, Эмиль ; Шрайер, Отто (1927), «Eine Kennzeichnung der reell abgeschlossenen Körper», Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg (на немецком языке), 5 : 225–231, doi : 10.1007/BF02952522, ISSN  0025-5858, JFM  53.0 144.01 , S2CID  121547404
• Акс, Джеймс (1968), «Элементарная теория конечных полей», Ann. of Math. , 2, 88 (2): 239–271, doi :10.2307/1970573, JSTOR  1970573
• Баез, Джон К. (2002), «Октонионы», Бюллетень Американского математического общества , 39 (2): 145–205, arXiv : math/0105155 , doi :10.1090/S0273-0979-01-00934-X, S2CID  586512
• Банашевски, Бернхард (1992), «Алгебраическое замыкание без выбора», Z. Math. Logik Grundlagen Math. , 38 (4): 383–385, doi :10.1002/malq.19920380136, Zbl  0739.03027
• Бичи, Джон А.; Блэр, Уильям Д. (2006), Абстрактная алгебра (3-е изд.), Waveland Press, ISBN 1-57766-443-4
• Блит, ТС; Робертсон, ЭФ (1985), Группы, кольца и поля: алгебра через практику , Cambridge University Press. См. особенно Книгу 3 ( ISBN 0-521-27288-2 ) и Книгу 6 ( ISBN 0-521-27291-2 ).  
• Борсо, Фрэнсис; Джанелидзе, Джордж (2001), Теории Галуа , Cambridge University Press, ISBN 0-521-80309-8, ЗБЛ  0978.12004
• Бурбаки, Николя (1994), Элементы истории математики , Springer, doi :10.1007/978-3-642-61693-8, ISBN 3-540-19376-6, МР  1290116
• Бурбаки, Николя (1988), Алгебра II. Главы 4–7 , Springer, ISBN 0-387-19375-8
• Касселс, JWS (1986), Локальные поля , Студенческие тексты Лондонского математического общества, т. 3, Cambridge University Press, doi : 10.1017/CBO9781139171885, ISBN 0-521-30484-9, МР  0861410
• Кларк, А. (1984), Элементы абстрактной алгебры, серия Dover Books on Mathematics, Dover, ISBN 978-0-486-64725-8
• Конвей, Джон Хортон (1976), О числах и играх , Academic Press
• Корри, Лео (2004), Современная алгебра и возникновение математических структур (2-е изд.), Birkhäuser, ISBN 3-7643-7002-5, Збл  1044.01008
• Дирихле, Питер Густав Лежен (1871), Дедекинд, Рихард (редактор), Vorlesungen über Zahlentheorie (Лекции по теории чисел) (на немецком языке), том. 1 (2-е изд.), Брауншвейг, Германия: Фридрих Видег и Зон
• Эйзенбуд, Дэвид (1995), Коммутативная алгебра с точки зрения алгебраической геометрии , Graduate Texts in Mathematics , т. 150, Нью-Йорк: Springer-Verlag , doi :10.1007/978-1-4612-5350-1, ISBN 0-387-94268-8, г-н  1322960
• Эскофье, JP (2012), Теория Галуа , Springer, ISBN 978-1-4613-0191-2
• Фрейли, Джон Б. (1976), Первый курс абстрактной алгебры (2-е изд.), Чтение: Addison-Wesley , ISBN 0-201-01984-1
• Фрике, Роберт ; Вебер, Генрих Мартин (1924), Lehrbuch der Algebra (на немецком языке), Vieweg, JFM  50.0042.03
• Гувеа, Фернандо К. (1997),p -адические числа , Universitext (2-е изд.), Springer
• Gouvêa, Fernando Q. (2012), Руководство по группам, кольцам и полям , Математическая ассоциация Америки, ISBN 978-0-88385-355-9
• «Поле», Энциклопедия математики , EMS Press , 2001 [1994]
• Хензель, Курт (1904), «Über eine neue Begründung der Theorie der алгебраического Zahlen», Journal für die Reine und Angewandte Mathematik (на немецком языке), 128 : 1–32, ISSN  0075-4102, JFM  35.0227.01
• Якобсон, Натан (2009), Основы алгебры , т. 1 (2-е изд.), Довер, ISBN 978-0-486-47189-1
• Яннсен, Уве; Вингберг, Кей (1982), «Die Struktur der Absoluten Galoisgruppe 𝔭-adischer Zahlkörper. [Структура абсолютной группы Галуа полей 𝔭-адических чисел]», Invent. Математика. , 70 (1): 71–98, Bibcode : 1982InMat..70...71J, doi : 10.1007/bf01393199, MR  0679774, S2CID  119378923
• Кляйнер, Израиль (2007), Кляйнер, Израиль (ред.), История абстрактной алгебры , Биркхойзер, doi : 10.1007/978-0-8176-4685-1, ISBN 978-0-8176-4684-4, г-н  2347309
• Кирнан, Б. Мелвин (1971), «Развитие теории Галуа от Лагранжа до Артина», Архив истории точных наук , 8 (1–2): 40–154, doi :10.1007/BF00327219, MR  1554154, S2CID  121442989
• Кульман, Сальма (2000), Упорядоченные экспоненциальные поля , Монографии Института Филдса, т. 12, Американское математическое общество, ISBN 0-8218-0943-1, МР  1760173
• Ланг, Серж (2002), Алгебра , Graduate Texts in Mathematics, т. 211 (3-е изд.), Springer, doi : 10.1007/978-1-4613-0041-0, ISBN 0-387-95385-X
• Лидл, Рудольф; Нидеррайтер, Харальд (2008), Конечные поля (2-е изд.), Cambridge University Press, ISBN 978-0-521-06567-2, Збл  1139.11053
• Лоренц, Фалько (2008), Алгебра, Том II: Поля со структурами, алгебры и дополнительные темы , Springer, ISBN 978-0-387-72487-4
• Маркер, Дэвид; Мессмер, Маргит; Пиллэй, Ананд (2006), Модельная теория полей , Lecture Notes in Logic, т. 5 (2-е изд.), Ассоциация символической логики, CiteSeerX  10.1.1.36.8448 , ISBN 978-1-56881-282-3, МР  2215060
• Маккой, Нил Х. (1968), Введение в современную алгебру, пересмотренное издание , Бостон: Allyn and Bacon , LCCN  68015225
• Майнс, Рэй; Ричман, Фред; Рюйтенбург, Вим (1988), Курс конструктивной алгебры , Universitext, Springer, doi : 10.1007/978-1-4419-8640-5, ISBN 0-387-96640-4, МР  0919949
• Мур, Э. Гастингс (1893), «Дважды бесконечная система простых групп», Бюллетень Американского математического общества , 3 (3): 73–78, doi : 10.1090/S0002-9904-1893-00178-X , MR  1557275
• Престел, Александр (1984), Лекции по формально вещественным полям , Lecture Notes in Mathematics, т. 1093, Springer, doi :10.1007/BFb0101548, ISBN 3-540-13885-4, МР  0769847
• Рибенбойм, Пауло (1999), Теория классических оценок , Springer Monographs in Mathematics, Springer, doi :10.1007/978-1-4612-0551-7, ISBN 0-387-98525-5, г-н  1677964
• Шольце, Питер (2014), «Перфектоидные пространства и их приложения» (PDF) , Труды Международного конгресса математиков 2014 г., Кён Мун С.А., ISBN 978-89-6105-804-9
• Схоутенс, Ганс (2002), Использование ультрапроизведений в коммутативной алгебре , Lecture Notes in Mathematics, т. 1999, Springer, ISBN 978-3-642-13367-1
• Серр, Жан-Пьер (1996) [1978], Курс арифметики. Перевод Cours d'arithmetique , Graduate Text in Mathematics, т. 7 (2-е изд.), Springer, ISBN 9780387900407, ЗБЛ  0432.10001
• Серр, Жан-Пьер (1979), Локальные поля , Graduate Texts in Mathematics, т. 67, Springer, ISBN 0-387-90424-7, МР  0554237
• Серр, Жан-Пьер (1992), Темы теории Галуа , Jones and Bartlett Publishers, ISBN 0-86720-210-6, ЗБЛ  0746.12001
• Серр, Жан-Пьер (2002), Когомологии Галуа , Springer Monographs in Mathematics, Перевод с французского Патрика Иона , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-42192-4, MR  1867431, Zbl  1004.12003
• Шарп, Дэвид (1987), Кольца и факторизация , Cambridge University Press, ISBN 0-521-33718-6, ЗБЛ  0674.13008
• Стейниц, Эрнст (1910), «Алгебраическая теория полей» [Алгебраическая теория полей], Journal für die reine und angewandte Mathematik , 1910 (137): 167–309, doi : 10.1515/crll.1910.137.167, ISSN  0075- 4102, JFM  41.0445.03, S2CID  120807300
• Тит, Жак (1957), «Sur les Analogs Algébriques des Groupes Semi-Simple Complexes», Colloque d'algèbre Superieure, Tenu à Bruxelles du 19 или 22 декабря 1956, Centre Belge de Recherches Mathématiques Établissements Ceuterick, Лувен , Париж: Librairie Gauthier -Вилларс, стр. 261–289.
• ван дер Пут, М.; Зингер, М.Ф. (2003), Теория Галуа линейных дифференциальных уравнений, Grundlehren der mathematischen Wissenschaften, vol. 328, Спрингер
• фон Штаудт, Карл Георг Кристиан (1857), Beiträge zur Geometrie der Lage (Вклад в геометрию положения), том. 2, Нюрнберг (Германия): Бауэр и Распе
• Уоллес, ДАР (1998), Группы, кольца и поля , SUMS, т. 151, Springer
• Уорнер, Сет (1989), Топологические поля , Северная Голландия, ISBN 0-444-87429-1, Збл  0683.12014
• Вашингтон, Лоуренс К. (1997), Введение в циклотомические поля , Graduate Texts in Mathematics, т. 83 (2-е изд.), Springer-Verlag, doi : 10.1007/978-1-4612-1934-7, ISBN 0-387-94762-0, г-н  1421575
• Вебер, Генрих (1893), «Die allgemeinen Grundlagen der Galois'schen Gleichungstheorie», Mathematische Annalen (на немецком языке), 43 (4): 521–549, doi : 10.1007/BF01446451, ISSN  0025-5831, JFM  25.0137.01, S2CID  120528969

Внешние ссылки