риманово многообразие

Гладкое многообразие со внутренним произведением на каждом касательном пространстве

Скалярное произведение двух векторов, касающихся сферы , находящейся внутри трехмерного евклидова пространства, содержит информацию о длинах и угле между векторами. Скалярные произведения на каждой касательной плоскости , упакованные вместе в один математический объект, являются римановой метрикой.

В дифференциальной геометрии риманово многообразие — это геометрическое пространство , на котором определены многие геометрические понятия, такие как расстояние, углы, длина, объем и кривизна. Евклидово пространство , -сфера , гиперболическое пространство и гладкие поверхности в трехмерном пространстве, такие как эллипсоиды и параболоиды , являются примерами римановых многообразий . Римановы многообразия названы в честь немецкого математика Бернхарда Римана , который первым их концептуализировал. ${\displaystyle n}$

Формально риманова метрика (или просто метрика ) на гладком многообразии — это выбор внутреннего произведения для каждого касательного пространства многообразия. Риманово многообразие — это гладкое многообразие вместе с римановой метрикой. Методы дифференциального и интегрального исчисления используются для извлечения геометрических данных из римановой метрики. Например, интегрирование приводит к римановой функции расстояния, тогда как дифференцирование используется для определения кривизны и параллельного переноса.

Любая гладкая поверхность в трехмерном евклидовом пространстве является римановым многообразием с римановой метрикой, вытекающей из того, как она находится внутри окружающего пространства . То же самое верно для любого подмногообразия евклидова пространства любой размерности. Хотя Джон Нэш доказал, что каждое риманово многообразие возникает как подмногообразие евклидова пространства, и хотя некоторые римановы многообразия естественным образом проявляются или определяются таким образом, идея риманова многообразия подчеркивает внутреннюю точку зрения, которая определяет геометрические понятия непосредственно на самом абстрактном пространстве без ссылки на окружающее пространство. Во многих случаях, например, для гиперболического пространства и проективного пространства , римановы метрики более естественно определяются или строятся с использованием внутренней точки зрения. Кроме того, многие метрики на группах Ли и однородных пространствах определяются внутренне с помощью групповых действий для переноса скалярного произведения на одном касательном пространстве на все многообразие, а многие специальные метрики, такие как метрики постоянной скалярной кривизны и метрики Кэлера–Эйнштейна, строятся внутренне с помощью инструментов из уравнений с частными производными .

Риманова геометрия , изучение римановых многообразий, имеет глубокие связи с другими областями математики, включая геометрическую топологию , комплексную геометрию и алгебраическую геометрию . Приложения включают физику (особенно общую теорию относительности и калибровочную теорию ), компьютерную графику , машинное обучение и картографию . Обобщения римановых многообразий включают псевдоримановы многообразия , финслеровы многообразия и субримановы многообразия .

История

Римановы многообразия были впервые концептуализированы их тезкой, немецким математиком Бернхардом Риманом .

В 1827 году Карл Фридрих Гаусс открыл, что гауссова кривизна поверхности, вложенной в трехмерное пространство, зависит только от локальных измерений, выполненных внутри поверхности ( первая фундаментальная форма ). ^[1] Этот результат известен как Theorema Egregium («замечательная теорема» на латыни).

Карта, которая сохраняет локальные измерения поверхности, называется локальной изометрией . Назовите свойство поверхности внутренним свойством, если оно сохраняется локальными изометриями, и внешним свойством, если нет. На этом языке в Theorema Egregium говорится, что гауссова кривизна является внутренним свойством поверхностей.

Римановы многообразия и их кривизна были впервые нестрого введены Бернхардом Риманом в 1854 году. ^[2] Однако они не были формализованы до гораздо более позднего времени. Фактически, более примитивное понятие гладкого многообразия было впервые явно определено только в 1913 году в книге Германа Вейля . ^[2]

Эли Картан ввел связность Картана , одну из первых концепций связности . Леви -Чивита определил связность Леви-Чивита , специальную связность на римановом многообразии.

Альберт Эйнштейн использовал теорию псевдоримановых многообразий (обобщение римановых многообразий) для разработки общей теории относительности . В частности, уравнения поля Эйнштейна являются ограничениями на кривизну пространства-времени , которое является 4-мерным псевдоримановым многообразием.

Определение

Римановы метрики и римановы многообразия

Касательная плоскость сферы с двумя векторами в ней. Риманова метрика позволяет взять скалярное произведение этих векторов.

Пусть будет гладким многообразием . Для каждой точки существует связанное векторное пространство, называемое касательным пространством в точке . Векторы в рассматриваются как векторы, касательные к точке в точке . ${\displaystyle M}$ ${\displaystyle p\in M}$ ${\displaystyle T_{p}M}$ ${\displaystyle M}$ ${\displaystyle p}$ ${\displaystyle T_{p}M}$ ${\displaystyle M}$ ${\displaystyle p}$

Однако не оснащен внутренним произведением , измерительной линейкой, которая дает касательным векторам понятие длины и угла. Это важный недостаток, поскольку исчисление учит, что для вычисления длины кривой необходимо определить длину векторов, касательных к кривой. Риманова метрика помещает измерительную линейку на каждое касательное пространство. ${\displaystyle T_{p}M}$

Риманова метрика на присваивает каждому положительно определенное скалярное произведение гладким образом (см. раздел о регулярности ниже). ^[3] Это индуцирует норму, определяемую как . Гладкое многообразие, снабженное римановой метрикой, является римановым многообразием , обозначаемым . ^[3] Риманова метрика является частным случаем метрического тензора . ${\displaystyle g}$ ${\displaystyle M}$ ${\displaystyle p}$ ${\displaystyle g_{p}:T_{p}M\times T_{p}M\to \mathbb {R} }$ ${\displaystyle \|\cdot \|_{p}:T_{p}M\to \mathbb {R} }$ ${\displaystyle \|v\|_{p}={\sqrt {g_{p}(v,v)}}}$ ${\displaystyle M}$ ${\displaystyle g}$ ${\displaystyle (M,g)}$

Риманову метрику не следует путать с функцией расстояния метрического пространства , которая также называется метрикой.

Риманова метрика в координатах

Если гладкие локальные координаты на , то векторы ${\displaystyle (x^{1},\ldots ,x^{n}):U\to \mathbb {R} ^{n}}$ ${\displaystyle M}$

${\displaystyle \left\{{\frac {\partial }{\partial x^{1}}}{\Big |}_{p},\dotsc ,{\frac {\partial }{\partial x^{n}}}{\Big |}_{p}\right\}}$

образуют базис векторного пространства для любого . Относительно этого базиса можно определить компоненты римановой метрики в каждой точке по формуле ${\displaystyle T_{p}M}$ ${\displaystyle p\in U}$ ${\displaystyle p}$

${\displaystyle g_{ij}|_{p}:=g_{p}\left(\left.{\frac {\partial }{\partial x^{i}}}\right|_{p},\left.{\frac {\partial }{\partial x^{j}}}\right|_{p}\right)}$. ^[4]

Эти функции можно объединить в матричную функцию на . Требование, что это положительно-определенный внутренний продукт, тогда точно говорит, что эта матричная функция является симметричной положительно-определенной матрицей на . ${\displaystyle n^{2}}$ ${\displaystyle g_{ij}:U\to \mathbb {R} }$ ${\displaystyle n\times n}$ ${\displaystyle U}$ ${\displaystyle g_{p}}$ ${\displaystyle p}$

В терминах тензорной алгебры риманову метрику можно записать в терминах двойственного базиса кокасательного расслоения как ${\displaystyle \{dx^{1},\ldots ,dx^{n}\}}$

${\displaystyle g=\sum _{i,j}g_{ij}\,dx^{i}\otimes dx^{j}.}$^[4]

Регулярность римановой метрики

Риманова метрика непрерывна, если ее компоненты непрерывны в любой гладкой координатной карте Риманова метрика гладка , если ее компоненты гладки в любой гладкой координатной карте. Можно рассмотреть много других типов римановых метрик в этом духе, таких как липшицевы римановы метрики или измеримые римановы метрики. ${\displaystyle g}$ ${\displaystyle g_{ij}:U\to \mathbb {R} }$ ${\displaystyle (U,x).}$ ${\displaystyle g}$ ${\displaystyle g_{ij}}$

В геометрическом анализе существуют ситуации , в которых требуется рассмотреть негладкие римановы метрики. См., например, (Громов 1999) и (Ши и Там 2002). Однако в этой статье предполагается, что является гладким, если не указано иное. ${\displaystyle g}$

Музыкальный изоморфизм

По аналогии с тем, как скалярное произведение на векторном пространстве индуцирует изоморфизм между векторным пространством и его сопряженным пространством, заданным , риманова метрика индуцирует изоморфизм расслоений между касательным расслоением и кокасательным расслоением . А именно, если — риманова метрика, то ${\displaystyle v\mapsto \langle v,\cdot \rangle }$ ${\displaystyle g}$

${\displaystyle (p,v)\mapsto g_{p}(v,\cdot )}$

является изоморфизмом гладких векторных расслоений из касательного расслоения в кокасательное расслоение . ^[5] ${\displaystyle TM}$ ${\displaystyle T^{*}M}$

Изометрии

Изометрия — это функция между римановыми многообразиями, которая сохраняет всю структуру римановых многообразий. Если два римановых многообразия имеют изометрию между собой, они называются изометрическими , и они считаются одним и тем же многообразием для целей римановой геометрии.

В частности, если и — два римановых многообразия, то диффеоморфизм называется изометрией, если , ^[6] то есть, если ${\displaystyle (M,g)}$ ${\displaystyle (N,h)}$ ${\displaystyle f:M\to N}$ ${\displaystyle g=f^{\ast }h}$

${\displaystyle g_{p}(u,v)=h_{f(p)}(df_{p}(u),df_{p}(v))}$

для всех и Например, переносы и вращения являются изометриями евклидова пространства (которое будет определено вскоре) самому себе. ${\displaystyle p\in M}$ ${\displaystyle u,v\in T_{p}M.}$

Говорят, что гладкое отображение, не являющееся диффеоморфизмом, является локальной изометрией , если каждое имеет открытую окрестность такую, что является изометрией (и, следовательно, диффеоморфизмом). ^[6] ${\displaystyle f:M\to N,}$ ${\displaystyle p\in M}$ ${\displaystyle U}$ ${\displaystyle f:U\to f(U)}$

Объем

Ориентированное -мерное риманово многообразие имеет уникальную -форму, называемую римановой формой объема . ^[7] Риманова форма объема сохраняется изометриями, сохраняющими ориентацию. ^[8] Форма объема порождает меру , по которой можно интегрировать измеримые функции. ^{[ требуется ссылка ]} Если компактно , то объем равен . [ ^7] ${\displaystyle n}$ ${\displaystyle (M,g)}$ ${\displaystyle n}$ ${\displaystyle dV_{g}}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle \int _{M}dV_{g}}$

Примеры

Евклидово пространство

Пусть обозначают стандартные координаты на (Каноническая) евклидова метрика задается формулой ^[9] ${\displaystyle x^{1},\ldots ,x^{n}}$ ${\displaystyle \mathbb {R} ^{n}.}$ ${\displaystyle g^{\text{can}}}$

${\displaystyle g^{\text{can}}\left(\sum _{i}a_{i}{\frac {\partial }{\partial x^{i}}},\sum _{j}b_{j}{\frac {\partial }{\partial x^{j}}}\right)=\sum _{i}a_{i}b_{i}}$

или эквивалентно

${\displaystyle g^{\text{can}}=(dx^{1})^{2}+\cdots +(dx^{n})^{2}}$

или, что эквивалентно, его координатными функциями

${\displaystyle g_{ij}^{\text{can}}=\delta _{ij}}$где находится дельта Кронекера ${\displaystyle \delta _{ij}}$

которые вместе образуют матрицу

${\displaystyle (g_{ij}^{\text{can}})={\begin{pmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{pmatrix}}.}$

Риманово многообразие называется евклидовым пространством . ${\displaystyle (\mathbb {R} ^{n},g^{\text{can}})}$

Подмногообразия

-Сфера с круглой метрикой является вложенным римановым подмногообразием . ${\displaystyle n}$ ${\displaystyle S^{n}}$ ${\displaystyle \mathbb {R} ^{n+1}}$

Пусть будет римановым многообразием и пусть будет погруженным подмногообразием или вложенным подмногообразием . Обратный образ является римановой метрикой на и называется римановым подмногообразием . [ ^10] ${\displaystyle (M,g)}$ ${\displaystyle i:N\to M}$ ${\displaystyle M}$ ${\displaystyle i^{*}g}$ ${\displaystyle g}$ ${\displaystyle N}$ ${\displaystyle (N,i^{*}g)}$ ${\displaystyle (M,g)}$

В случае, когда , отображение задается как и метрика является просто ограничением на векторы, касательные вдоль . В общем случае формула для имеет вид ${\displaystyle N\subseteq M}$ ${\displaystyle i:N\to M}$ ${\displaystyle i(x)=x}$ ${\displaystyle i^{*}g}$ ${\displaystyle g}$ ${\displaystyle N}$ ${\displaystyle i^{*}g}$

${\displaystyle i^{*}g_{p}(v,w)=g_{i(p)}{\big (}di_{p}(v),di_{p}(w){\big )},}$

где находится pushforward от​ ${\displaystyle di_{p}(v)}$ ${\displaystyle v}$ ${\displaystyle i.}$

Примеры:

• -сфера​ ${\displaystyle n}$

  ${\displaystyle S^{n}=\{x\in \mathbb {R} ^{n+1}:(x^{1})^{2}+\cdots +(x^{n+1})^{2}=1\}}$

является гладким вложенным подмногообразием евклидова пространства . ^[11] Риманова метрика, которую это индуцирует, называется круглой метрикой или стандартной метрикой . ${\displaystyle \mathbb {R} ^{n+1}}$ ${\displaystyle S^{n}}$

• Исправьте действительные числа . Эллипсоид ${\displaystyle a,b,c}$

  ${\displaystyle \left\{(x,y,z)\in \mathbb {R} ^{3}:{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1\right\}}$

является гладким вложенным подмногообразием евклидова пространства . ${\displaystyle \mathbb {R} ^{3}}$

• График гладкой функции представляет собой гладкое вложенное подмногообразие со своей стандартной метрикой. ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$ ${\displaystyle \mathbb {R} ^{n+1}}$
• Если не является односвязным, то существует накрывающее отображение , где — универсальное накрытие . Это погружение (так как локально оно является диффеоморфизмом), поэтому автоматически наследует риманову метрику. По тому же принципу любое гладкое накрывающее пространство риманова многообразия наследует риманову метрику. ${\displaystyle (M,g)}$ ${\displaystyle {\widetilde {M}}\to M}$ ${\displaystyle {\widetilde {M}}}$ ${\displaystyle M}$ ${\displaystyle {\widetilde {M}}}$

С другой стороны, если уже имеет риманову метрику , то погружение (или вложение) называется изометрическим погружением (или изометрическим вложением ), если . Следовательно, изометрические погружения и изометрические вложения являются римановыми подмногообразиями. ^[10] ${\displaystyle N}$ ${\displaystyle {\tilde {g}}}$ ${\displaystyle i:N\to M}$ ${\displaystyle {\tilde {g}}=i^{*}g}$

Продукция

Тор естественным образом несет евклидову метрику, полученную путем отождествления противоположных сторон квадрата (слева). Полученное риманово многообразие, называемое плоским тором , не может быть изометрически вложено в трехмерное евклидово пространство (справа), поскольку для этого необходимо сгибать и растягивать лист. Таким образом, внутренняя геометрия плоского тора отличается от геометрии вложенного тора.

Пусть и будут двумя римановыми многообразиями, и рассмотрим произведение многообразий . Римановы метрики и естественным образом накладывают риманову метрику, на которой можно описать несколькими способами. ${\displaystyle (M,g)}$ ${\displaystyle (N,h)}$ ${\displaystyle M\times N}$ ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle {\widetilde {g}}}$ ${\displaystyle M\times N,}$

• Рассматривая разложение, можно определить ${\displaystyle T_{(p,q)}(M\times N)\cong T_{p}M\oplus T_{q}N,}$

  ${\displaystyle {\widetilde {g}}_{p,q}((u_{1},u_{2}),(v_{1},v_{2}))=g_{p}(u_{1},v_{1})+h_{q}(u_{2},v_{2}).}$^[12]

• Если — гладкая координатная карта на и — гладкая координатная карта на , то — гладкая координатная карта на Пусть будет представлением на карте и пусть будет представлением на карте . Представление в координатах равно ${\displaystyle (U,x)}$ ${\displaystyle M}$ ${\displaystyle (V,y)}$ ${\displaystyle N}$ ${\displaystyle (U\times V,(x,y))}$ ${\displaystyle M\times N.}$ ${\displaystyle g_{U}}$ ${\displaystyle g}$ ${\displaystyle (U,x)}$ ${\displaystyle h_{V}}$ ${\displaystyle h}$ ${\displaystyle (V,y)}$ ${\displaystyle {\widetilde {g}}}$ ${\displaystyle (U\times V,(x,y))}$

  ${\displaystyle {\widetilde {g}}=\sum _{ij}{\widetilde {g}}_{ij}\,dx^{i}\,dx^{j}}$где ^[12] ${\displaystyle ({\widetilde {g}}_{ij})={\begin{pmatrix}g_{U}&0\\0&h_{V}\end{pmatrix}}.}$

Например, рассмотрим -тор . Если каждой копии задана круглая метрика, то произведение риманово многообразие называется плоским тором . В качестве другого примера, риманово произведение , где каждая копия имеет евклидову метрику, изометрично с евклидовой метрикой. ${\displaystyle n}$ ${\displaystyle T^{n}=S^{1}\times \cdots \times S^{1}}$ ${\displaystyle S^{1}}$ ${\displaystyle T^{n}}$ ${\displaystyle \mathbb {R} \times \cdots \times \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} ^{n}}$

Положительные комбинации показателей

Пусть — риманова метрика на Если — любые положительные гладкие функции на , то — другая риманова метрика на ${\displaystyle g_{1},\ldots ,g_{k}}$ ${\displaystyle M.}$ ${\displaystyle f_{1},\ldots ,f_{k}}$ ${\displaystyle M}$ ${\displaystyle f_{1}g_{1}+\ldots +f_{k}g_{k}}$ ${\displaystyle M.}$

Каждое гладкое многообразие допускает риманову метрику

Теорема: Каждое гладкое многообразие допускает (неканоническую) риманову метрику. ^[13]

Это фундаментальный результат. Хотя большая часть базовой теории римановых метрик может быть разработана с использованием только того, что гладкое многообразие является локально евклидовым топологическим пространством, для этого результата необходимо использовать то, что гладкие многообразия являются хаусдорфовыми и паракомпактными . Причина в том, что доказательство использует разбиение единицы .

Альтернативное доказательство использует теорему вложения Уитни для вложения в евклидово пространство, а затем возвращает метрику из евклидова пространства в . С другой стороны, теорема вложения Нэша утверждает, что для любого гладкого риманова многообразия существует вложение для некоторого такого, что обратный откат на стандартной римановой метрики на равен То есть вся структура гладкого риманова многообразия может быть закодирована диффеоморфизмом в определенное вложенное подмногообразие некоторого евклидова пространства. Поэтому можно утверждать, что ничего нельзя получить из рассмотрения абстрактных гладких многообразий и их римановых метрик. Однако существует много естественных гладких римановых многообразий, таких как множество вращений трехмерного пространства и гиперболического пространства, любое представление которых в виде подмногообразия евклидова пространства не сможет представить их замечательные симметрии и свойства так же ясно, как это делают их абстрактные представления. ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle (M,g),}$ ${\displaystyle F:M\to \mathbb {R} ^{N}}$ ${\displaystyle N}$ ${\displaystyle F}$ ${\displaystyle \mathbb {R} ^{N}}$ ${\displaystyle g.}$

Структура метрического пространства

Допустимая кривая — это кусочно-гладкая кривая , скорость которой ненулевая всюду, где она определена. Неотрицательная функция определена на интервале, за исключением конечного числа точек. Длина допустимой кривой определяется как ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma '(t)\in T_{\gamma (t)}M}$ ${\displaystyle t\mapsto \|\gamma '(t)\|_{\gamma (t)}}$ ${\displaystyle [0,1]}$ ${\displaystyle L(\gamma )}$ ${\displaystyle \gamma :[0,1]\to M}$

${\displaystyle L(\gamma )=\int _{0}^{1}\|\gamma '(t)\|_{\gamma (t)}\,dt.}$

Подынтегральное выражение ограничено и непрерывно, за исключением конечного числа точек, поэтому оно интегрируемо. Для связного риманова многообразия определим как ${\displaystyle (M,g)}$ ${\displaystyle d_{g}:M\times M\to [0,\infty )}$

${\displaystyle d_{g}(p,q)=\inf\{L(\gamma ):\gamma {\text{ an admissible curve with }}\gamma (0)=p,\gamma (1)=q\}.}$

Теорема: является метрическим пространством , а метрическая топология на совпадает с топологией на . ^[14] ${\displaystyle (M,d_{g})}$ ${\displaystyle (M,d_{g})}$ ${\displaystyle M}$

Хотя длина кривой задается явной формулой, как правило, невозможно выписать функцию расстояния какими-либо явными средствами. Фактически, если компактно, всегда существуют точки, где недифференцируемо, и может быть чрезвычайно сложно даже определить местоположение или природу этих точек, даже в, казалось бы, простых случаях, например, когда является эллипсоидом. ^{[ необходима цитата ]} ${\displaystyle d_{g}}$ ${\displaystyle M}$ ${\displaystyle d_{g}:M\times M\to \mathbb {R} }$ ${\displaystyle (M,g)}$

Если работать с римановыми метриками, которые являются просто непрерывными, но, возможно, не гладкими, то длина допустимой кривой и функция риманова расстояния определяются точно так же и, как и прежде, являются метрическим пространством , а метрическая топология на совпадает с топологией на . ^[15] ${\displaystyle (M,d_{g})}$ ${\displaystyle (M,d_{g})}$ ${\displaystyle M}$

Диаметр

Диаметр метрического пространства равен ${\displaystyle (M,d_{g})}$

${\displaystyle \operatorname {diam} (M,d_{g})=\sup\{d_{g}(p,q):p,q\in M\}.}$

Теорема Хопфа–Ринова показывает, что если является полным и имеет конечный диаметр, то оно компактно. Обратно, если является компактным, то функция имеет максимум, поскольку является непрерывной функцией на компактном метрическом пространстве. Это доказывает следующее. ${\displaystyle (M,d_{g})}$ ${\displaystyle (M,d_{g})}$ ${\displaystyle d_{g}:M\times M\to \mathbb {R} }$

Если является полным, то оно компактно тогда и только тогда, когда оно имеет конечный диаметр. ${\displaystyle (M,d_{g})}$

Это не так без предположения о полноте; для контрпримеров можно рассмотреть любое открытое ограниченное подмножество евклидова пространства со стандартной римановой метрикой. Также неверно, что любое полное метрическое пространство конечного диаметра должно быть компактным; важно, что метрическое пространство произошло из риманова многообразия.

Связи, геодезические и кривизна

Связи

(Аффинная) связность — это дополнительная структура на римановом многообразии, которая определяет дифференциацию одного векторного поля относительно другого. Связи содержат геометрические данные, и два римановых многообразия с разными связями имеют разную геометрию.

Пусть обозначает пространство векторных полей на . (Аффинная) связность ${\displaystyle {\mathfrak {X}}(M)}$ ${\displaystyle M}$

${\displaystyle \nabla :{\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\to {\mathfrak {X}}(M)}$

на — это билинейное отображение, такое что ${\displaystyle M}$ ${\displaystyle (X,Y)\mapsto \nabla _{X}Y}$

1. Для каждой функции , ${\displaystyle f\in C^{\infty }(M)}$ ${\displaystyle \nabla _{f_{1}X_{1}+f_{2}X_{2}}Y=f_{1}\,\nabla _{X_{1}}Y+f_{2}\,\nabla _{X_{2}}Y,}$
2. Правило произведения сохраняется. ^[16] ${\displaystyle \nabla _{X}fY=X(f)Y+f\,\nabla _{X}Y}$

Выражение называется ковариантной производной по . ${\displaystyle \nabla _{X}Y}$ ${\displaystyle Y}$ ${\displaystyle X}$

Связь Леви-Чивита

Два римановых многообразия с разными связями имеют разную геометрию. К счастью, существует естественная связь, связанная с римановым многообразием, называемая связностью Леви-Чивиты .

Говорят, что соединение сохраняет метрику, если ${\displaystyle \nabla }$

${\displaystyle X{\bigl (}g(Y,Z){\bigr )}=g(\nabla _{X}Y,Z)+g(Y,\nabla _{X}Z)}$

Соединение не имеет кручения, если ${\displaystyle \nabla }$

${\displaystyle \nabla _{X}Y-\nabla _{Y}X=[X,Y],}$

где находится скобка Ли . ${\displaystyle [\cdot ,\cdot ]}$

Связность Леви-Чивиты — это связь без кручения, которая сохраняет метрику. Как только риманова метрика зафиксирована, существует единственная связь Леви-Чивиты. ^[17] Обратите внимание, что определение сохранения метрики использует регулярность . ${\displaystyle g}$

Ковариантная производная вдоль кривой

Если — гладкая кривая, то гладкое векторное поле вдоль — это гладкое отображение, такое что для всех . Множество гладких векторных полей вдоль — это векторное пространство относительно поточечного сложения векторов и скалярного умножения. ^[18] Можно также поточечно умножить гладкое векторное поле вдоль на гладкую функцию : ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma }$ ${\displaystyle X:[0,1]\to TM}$ ${\displaystyle X(t)\in T_{\gamma (t)}M}$ ${\displaystyle t\in [0,1]}$ ${\displaystyle {\mathfrak {X}}(\gamma )}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle f:[0,1]\to \mathbb {R} }$

${\displaystyle (fX)(t)=f(t)X(t)}$для ${\displaystyle X\in {\mathfrak {X}}(\gamma ).}$

Пусть — гладкое векторное поле вдоль . Если — гладкое векторное поле в окрестности образа , такое что , то называется расширением . ${\displaystyle X}$ ${\displaystyle \gamma }$ ${\displaystyle {\tilde {X}}}$ ${\displaystyle \gamma }$ ${\displaystyle X(t)={\tilde {X}}_{\gamma (t)}}$ ${\displaystyle {\tilde {X}}}$ ${\displaystyle X}$

При наличии фиксированной связи на и гладкой кривой существует единственный оператор , называемый ковариантной производной вдоль , такой, что: ^[19] ${\displaystyle \nabla }$ ${\displaystyle M}$ ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle D_{t}:{\mathfrak {X}}(\gamma )\to {\mathfrak {X}}(\gamma )}$ ${\displaystyle \gamma }$

1. ${\displaystyle D_{t}(aX+bY)=a\,D_{t}X+b\,D_{t}Y,}$
2. ${\displaystyle D_{t}(fX)=f'X+f\,D_{t}X,}$
3. Если является расширением , то . ${\displaystyle {\tilde {X}}}$ ${\displaystyle X}$ ${\displaystyle D_{t}X(t)=\nabla _{\gamma '(t)}{\tilde {X}}}$

Геодезические

В евклидовом пространстве (слева) максимальные геодезические — прямые линии. В круглой сфере (справа) максимальные геодезические — большие окружности . ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle S^{n}}$

Геодезические — это кривые без внутреннего ускорения. Эквивалентно, геодезические — это кривые, которые локально выбирают кратчайший путь между двумя точками. Они являются обобщением прямых линий в евклидовом пространстве на произвольные римановы многообразия. Муравей, живущий в римановом многообразии и идущий прямо вперед, не прилагая никаких усилий для ускорения или поворота, прочертит геодезическую.

Зафиксируем связь на . Пусть будет гладкой кривой. Ускорение — векторное поле вдоль . Если для всех , называется геодезической . ^[20] ${\displaystyle \nabla }$ ${\displaystyle M}$ ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma }$ ${\displaystyle D_{t}\gamma '}$ ${\displaystyle \gamma }$ ${\displaystyle D_{t}\gamma '=0}$ ${\displaystyle t}$ ${\displaystyle \gamma }$

Для каждого и существует геодезическая, определенная на некотором открытом интервале, содержащем 0, такая, что и . Любые две такие геодезические совпадают в своей общей области определения. ^[21] Взяв объединение по всем открытым интервалам, содержащим 0, на которых существует геодезическая, удовлетворяющая и , получаем геодезическую, называемую максимальной геодезической , каждая геодезическая, удовлетворяющая и , является ограничением. ^[22] ${\displaystyle p\in M}$ ${\displaystyle v\in T_{p}M}$ ${\displaystyle \gamma :I\to M}$ ${\displaystyle I}$ ${\displaystyle \gamma (0)=p}$ ${\displaystyle \gamma '(0)=v}$ ${\displaystyle I}$ ${\displaystyle \gamma (0)=p}$ ${\displaystyle \gamma '(0)=v}$ ${\displaystyle \gamma (0)=p}$ ${\displaystyle \gamma '(0)=v}$

Каждая кривая , имеющая наименьшую длину среди всех допустимых кривых с теми же конечными точками, что и , является геодезической (в перепараметризации с единичной скоростью). ^[23] ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma }$

Примеры

• Непостоянные максимальные геодезические линии евклидовой плоскости — это в точности прямые линии. ^[22] Это согласуется с фактом из евклидовой геометрии, что кратчайший путь между двумя точками — это отрезок прямой линии. ${\displaystyle \mathbb {R} ^{2}}$
• Непостоянные максимальные геодезические с круглой метрикой — это в точности большие окружности . ^[24] Поскольку Земля имеет приблизительно сферическую форму, это означает, что кратчайший путь, по которому самолет может пролететь между двумя точками на Земле, — это сегмент большого круга. ${\displaystyle S^{2}}$

Теорема Хопфа–Ринова

Проколотая плоскость не является геодезически полной , поскольку максимальная геодезическая с начальными условиями не имеет области определения . ${\displaystyle \mathbb {R} ^{2}\backslash \{(0,0)\}}$ ${\displaystyle p=(1,1)}$ ${\displaystyle v=(1,1)}$ ${\displaystyle \mathbb {R} }$

Риманово многообразие со связностью Леви-Чивиты геодезически полно, если область определения каждой максимальной геодезической равна . ^[25] Плоскость геодезически полна. С другой стороны, проколотая плоскость с ограничением римановой метрики из не является геодезически полной, поскольку максимальная геодезическая с начальными условиями не имеет области определения . ${\displaystyle M}$ ${\displaystyle (-\infty ,\infty )}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{2}\smallsetminus \{(0,0)\}}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle p=(1,1)}$ ${\displaystyle v=(1,1)}$ ${\displaystyle \mathbb {R} }$

Теорема Хопфа –Ринова характеризует геодезически полные многообразия.

Теорема: Пусть — связное риманово многообразие. Следующие утверждения эквивалентны: ^[26] ${\displaystyle (M,g)}$

• Метрическое пространство является полным (каждая последовательность Коши сходится), ${\displaystyle (M,d_{g})}$ ${\displaystyle d_{g}}$
• Все замкнутые и ограниченные подмножества компактны, ${\displaystyle M}$
• ${\displaystyle M}$является геодезически полным.

Параллельный транспорт

Параллельный перенос касательного вектора вдоль кривой в сфере.

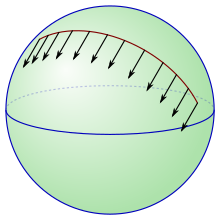
В евклидовом пространстве все касательные пространства канонически отождествляются друг с другом посредством переноса, поэтому легко перемещать векторы из одного касательного пространства в другое. Параллельный перенос — это способ перемещения векторов из одного касательного пространства в другое вдоль кривой в условиях общего риманова многообразия. При наличии фиксированного соединения существует единственный способ выполнить параллельный перенос. ^[27]

В частности, назовем гладкое векторное поле вдоль гладкой кривой параллельным вдоль , если тождественно. ^[22] Зафиксируем кривую с и . Чтобы параллельно перенести вектор в вектор вдоль , сначала расширьте его до векторного поля, параллельного вдоль , а затем возьмите значение этого векторного поля в . ${\displaystyle V}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle D_{t}V=0}$ ${\displaystyle \gamma :[0,1]\to M}$ ${\displaystyle \gamma (0)=p}$ ${\displaystyle \gamma (1)=q}$ ${\displaystyle v\in T_{p}M}$ ${\displaystyle T_{q}M}$ ${\displaystyle \gamma }$ ${\displaystyle v}$ ${\displaystyle \gamma }$ ${\displaystyle q}$

На рисунках ниже показан параллельный перенос, вызванный связностью Леви-Чивиты, связанный с двумя различными римановыми метриками на проколотой плоскости . Кривая, вдоль которой осуществляется параллельный перенос, является единичной окружностью. В полярных координатах метрика слева является стандартной евклидовой метрикой , тогда как метрика справа — . Эта вторая метрика имеет особенность в начале координат, поэтому она не распространяется за прокол, но первая метрика распространяется на всю плоскость. ${\displaystyle \mathbb {R} ^{2}\smallsetminus \{0,0\}}$ ${\displaystyle dx^{2}+dy^{2}=dr^{2}+r^{2}\,d\theta ^{2}}$ ${\displaystyle dr^{2}+d\theta ^{2}}$

Параллельные переносы на проколотой плоскости в связях Леви-Чивита

Предупреждение: Это параллельный перенос на проколотой плоскости вдоль единичной окружности, а не параллельный перенос на единичной окружности. Действительно, на первом изображении векторы выходят за пределы касательного пространства к единичной окружности.

Тензор кривизны Римана

Тензор кривизны Римана точно измеряет степень, в которой параллельные переносящие векторы вокруг небольшого прямоугольника не являются тождественным отображением. ^[28] Тензор кривизны Римана равен 0 в каждой точке тогда и только тогда, когда многообразие локально изометрично евклидову пространству. ^[29]

Зафиксируем связь на . Тензор кривизны Римана — это отображение, определяемое формулой ${\displaystyle \nabla }$ ${\displaystyle M}$ ${\displaystyle R:{\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\to {\mathfrak {X}}(M)}$

${\displaystyle R(X,Y)Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X,Y]}Z}$

где - скобка Ли векторных полей . Тензор кривизны Римана - это -тензорное поле. ^[30] ${\displaystyle [X,Y]}$ ${\displaystyle (1,3)}$

Тензор кривизны Риччи

Зафиксируем связь на . Тензор кривизны Риччи равен ${\displaystyle \nabla }$ ${\displaystyle M}$

${\displaystyle Ric(X,Y)=\operatorname {tr} (Z\mapsto R(Z,X)Y)}$

где — след. Тензор кривизны Риччи — это ковариантное 2-тензорное поле. ^[31] ${\displaystyle \operatorname {tr} }$

Многообразия Эйнштейна

Тензор кривизны Риччи играет определяющую роль в теории многообразий Эйнштейна , которая имеет приложения к изучению гравитации . (Псевдо)риманова метрика называется метрикой Эйнштейна, если уравнение Эйнштейна ${\displaystyle Ric}$ ${\displaystyle g}$

${\displaystyle Ric=\lambda g}$для некоторой константы ${\displaystyle \lambda }$

выполняется, и (псевдо)риманово многообразие, метрика которого является эйнштейновой, называется многообразием Эйнштейна . ^[32] Примерами многообразий Эйнштейна являются евклидово пространство, -сфера, гиперболическое пространство и комплексное проективное пространство с метрикой Фубини-Штуди . ${\displaystyle n}$

Скалярная кривизна

Постоянная кривизна и формы пространства

Говорят, что риманово многообразие имеет постоянную кривизну κ , если каждая секционная кривизна равна числу κ . Это эквивалентно условию, что относительно любой координатной карты тензор кривизны Римана может быть выражен через метрический тензор как

${\displaystyle R_{ijkl}=\kappa (g_{il}g_{jk}-g_{ik}g_{jl}).}$

Это подразумевает, что кривизна Риччи задается как R _jk = ( n – 1) κg _jk , а скалярная кривизна равна n ( n – 1) κ , где n – размерность многообразия. В частности, каждое риманово многообразие постоянной кривизны является многообразием Эйнштейна , тем самым имея постоянную скалярную кривизну. Как обнаружил Бернхард Риман в своей лекции 1854 года, вводящей риманову геометрию, локально определенная риманова метрика

${\displaystyle {\frac {dx_{1}^{2}+\cdots +dx_{n}^{2}}{(1+{\frac {\kappa }{4}}(x_{1}^{2}+\cdots +x_{n}^{2}))^{2}}}}$

имеет постоянную кривизну κ . Любые два римановых многообразия одинаковой постоянной кривизны локально изометричны , и отсюда следует, что любое риманово многообразие постоянной кривизны κ может быть покрыто координатными картами, относительно которых метрика имеет указанный выше вид. ^[33]

Риманова пространственная форма — это риманово многообразие с постоянной кривизной, которое дополнительно связно и геодезически полно . Риманова пространственная форма называется сферической пространственной формой , если кривизна положительна, евклидовой пространственной формой , если кривизна равна нулю, и гиперболической пространственной формой или гиперболическим многообразием , если кривизна отрицательна. В любом измерении сфера со своей стандартной римановой метрикой, евклидово пространство и гиперболическое пространство являются римановыми пространственными формами постоянной кривизны 1 , 0 и –1 соответственно. Кроме того, теорема Киллинга–Хопфа гласит, что любая односвязная сферическая пространственная форма гомотетична сфере, любая односвязная евклидова пространственная форма гомотетична евклидову пространству, а любая односвязная гиперболическая пространственная форма гомотетична гиперболическому пространству. ^[33]

Используя конструкцию покрывающего многообразия , любая риманова пространственная форма изометрична фактор-многообразию односвязной римановой пространственной формы по модулю определенного группового действия изометрий. Например, группа изометрий n -сферы является ортогональной группой O( n + 1) . Если задана любая ее конечная подгруппа G , в которой только единичная матрица имеет 1 в качестве собственного значения , естественное групповое действие ортогональной группы на n -сфере ограничивается групповым действием G , причем фактор-многообразие S ⁿ / G наследует геодезически полную риманову метрику постоянной кривизны 1 . С точностью до гомотетии каждая сферическая пространственная форма возникает таким образом; это в значительной степени сводит изучение сферических пространственных форм к проблемам теории групп . Например, это можно использовать, чтобы напрямую показать, что каждая четномерная сферическая пространственная форма гомотетична стандартной метрике либо на сфере, либо на вещественном проективном пространстве . Существует еще много нечетномерных сферических пространственных форм, хотя известны алгоритмы их классификации. Список трехмерных сферических пространственных форм бесконечен, но явно известен и включает в себя линзовые пространства и додекаэдрическое пространство Пуанкаре . ^[34]

Случай евклидовых и гиперболических пространственных форм также может быть сведен к теории групп, основанной на изучении группы изометрий евклидова пространства и гиперболического пространства. Например, класс двумерных евклидовых пространственных форм включает римановы метрики на ^{бутылке} Клейна , ленте Мёбиуса , торе , цилиндре S1 × ℝ , а также евклидовой плоскости. В отличие от случая двумерных сферических пространственных форм, в некоторых случаях две структуры пространственных форм на одном и том же многообразии не являются гомотетичными. Случай двумерных гиперболических пространственных форм еще более сложен, имея дело с пространством Тейхмюллера . В трех измерениях евклидовы пространственные формы известны, в то время как геометрия гиперболических пространственных форм в трех и более измерениях остается областью активных исследований, известной как гиперболическая геометрия . ^[35]

Римановы метрики на группах Ли

Левоинвариантные метрики на группах Ли

Пусть G — группа Ли , например, группа вращений в трехмерном пространстве . Используя структуру группы, любое скалярное произведение на касательном пространстве в тождестве (или любом другом конкретном касательном пространстве) можно перенести на все другие касательные пространства, чтобы определить риманову метрику. Формально, если дано скалярное произведение g _e на касательном пространстве в тождестве, скалярное произведение на касательном пространстве в произвольной точке p определяется как

${\displaystyle g_{p}(u,v)=g_{e}(dL_{p^{-1}}(u),dL_{p^{-1}}(v)),}$

где для произвольного x , L _x — это левое отображение умножения G → G, переводящее точку y в xy . Римановы метрики, построенные таким образом, являются левоинвариантными ; правоинвариантные римановы метрики могут быть построены аналогичным образом с использованием правого отображения умножения.

Связность Леви-Чивиты и кривизна общей левоинвариантной римановой метрики могут быть вычислены явно в терминах g _e , присоединенного представления G и алгебры Ли, связанной с G . ^[36] Эти формулы значительно упрощаются в частном случае римановой метрики, которая является биинвариантной (то есть одновременно лево- и правоинвариантной). ^[37] Все левоинвариантные метрики имеют постоянную скалярную кривизну.

Левоинвариантные и биинвариантные метрики на группах Ли являются важным источником примеров римановых многообразий. Сферы Берже , построенные как левоинвариантные метрики на специальной унитарной группе SU(2), являются одними из простейших примеров явлений коллапса , в которых односвязное риманово многообразие может иметь малый объем, не имея большой кривизны. ^[38] Они также дают пример римановой метрики, которая имеет постоянную скалярную кривизну, но которая не является эйнштейновой или даже параллельной кривизной Риччи. ^[39] Гиперболическому пространству можно задать структуру группы Ли, относительно которой метрика является левоинвариантной. ^{[40] [41]} Любая биинвариантная риманова метрика на группе Ли имеет неотрицательную секционную кривизну, что дает множество таких метрик: группе Ли можно задать биинвариантную риманову метрику тогда и только тогда, когда она является произведением компактной группы Ли на абелеву группу Ли . ^[42]

Однородные пространства

Говорят, что риманово многообразие ( M , g ) является однородным , если для каждой пары точек x и y в M существует некоторая изометрия f риманова многообразия, переводящая x в y . Это можно перефразировать на языке групповых действий как требование, чтобы естественное действие группы изометрий было транзитивным. Каждое однородное риманово многообразие является геодезически полным и имеет постоянную скалярную кривизну. ^[43]

С точностью до изометрии все однородные римановы многообразия возникают с помощью следующей конструкции. Для данной группы Ли G с компактной подгруппой K , которая не содержит никакой нетривиальной нормальной подгруппы G , зафиксируем любое дополняемое подпространство W алгебры Ли K внутри алгебры Ли G. Если это подпространство инвариантно относительно линейного отображения ad _G ( k ): W → W для любого элемента k из K , то G -инвариантные римановы метрики на пространстве смежных классов G / K находятся во взаимно однозначном соответствии с теми скалярными произведениями на W, которые инвариантны относительно ad _G ( k ): W → W для каждого элемента k из K. ^[44] Каждая такая риманова метрика однородна, при этом G естественным образом рассматривается как подгруппа полной группы изометрий .

Приведенный выше пример групп Ли с левоинвариантными римановыми метриками возникает как очень частный случай этой конструкции, а именно, когда K является тривиальной подгруппой, содержащей только единичный элемент. Вычисления связности Леви-Чивиты и кривизны, упомянутые там, могут быть обобщены на этот контекст, где теперь вычисления формулируются в терминах скалярного произведения на W , алгебры Ли G , и разложения прямой суммы алгебры Ли G в алгебры Ли K и W . ^[44] Это сводит изучение кривизны однородных римановых многообразий в значительной степени к алгебраическим проблемам. Это сокращение, вместе с гибкостью приведенной выше конструкции, делает класс однородных римановых многообразий очень полезным для построения примеров.

Симметричные пространства

Связное риманово многообразие ( M , g ) называется симметричным , если для каждой точки p из M существует некоторая изометрия многообразия с p в качестве неподвижной точки и для которой отрицание дифференциала в p является тождественным отображением . Каждое риманово симметрическое пространство однородно и, следовательно, геодезически полно и имеет постоянную скалярную кривизну. Однако римановы симметрические пространства также обладают гораздо более сильным свойством кривизны, которым не обладают большинство однородных римановых многообразий, а именно, что тензор кривизны Римана и кривизна Риччи параллельны . Римановы многообразия с этим свойством кривизны, которое можно было бы вольно сформулировать как «постоянный тензор кривизны Римана» (не путать с постоянной кривизной ), называются локально симметричными . Это свойство почти характеризует симметрические пространства; Эли Картан доказал в 1920-х годах, что локально симметричное риманово многообразие, которое является геодезически полным и односвязным , на самом деле должно быть симметричным. ^[45]

Многие из основных примеров римановых многообразий симметричны. Наиболее основные включают сферу и вещественные проективные пространства с их стандартными метриками, а также гиперболическое пространство. Комплексное проективное пространство, кватернионное проективное пространство и плоскость Кэли являются аналогами вещественного проективного пространства, которые также симметричны, как и комплексное гиперболическое пространство , кватернионное гиперболическое пространство и гиперболическое пространство Кэли, которые вместо этого являются аналогами гиперболического пространства. Грассмановы многообразия также несут естественные римановы метрики, превращающие их в симметричные пространства. Среди групп Ли с левоинвариантными римановыми метриками те, которые являются биинвариантными, являются симметричными. ^[45]

Основываясь на их алгебраической формулировке как особых видов однородных пространств, Картан добился явной классификации симметричных пространств, которые являются неприводимыми , ссылаясь на те, которые не могут быть локально разложены как пространства произведений . Каждое такое пространство является примером многообразия Эйнштейна ; среди них только одномерные многообразия имеют нулевую скалярную кривизну. Эти пространства важны с точки зрения римановой голономии . Как обнаружил в 1950-х годах Марсель Берже , любое риманово многообразие, которое является односвязным и неприводимым, является либо симметричным пространством, либо имеет риманову голономию, принадлежащую списку всего из семи возможностей. Шесть из семи исключений из симметричных пространств в классификации Бергера попадают в области кэлеровой геометрии , кватернионно-кэлеровой геометрии , геометрии G 2 и геометрии Spin(7) , каждая из которых изучает римановы многообразия, снабженные определенными дополнительными структурами и симметриями. Седьмое исключение — это изучение «общих» римановых многообразий без особой симметрии, что отражается в максимально возможной группе голономии. ^[45]

Бесконечномерные многообразия

Приведенные выше утверждения и теоремы относятся к конечномерным многообразиям — многообразиям, карты которых отображаются в открытые подмножества Их можно в определенной степени расширить до бесконечномерных многообразий; то есть многообразий, которые моделируются по образцу топологического векторного пространства ; например, многообразия Фреше , Банаха и Гильберта . ${\displaystyle \mathbb {R} ^{n}.}$

Определения

Римановы метрики определяются аналогично конечномерному случаю. Однако существует различие между двумя типами римановых метрик:

• Слабая риманова метрика на — это гладкая функция , такая что для любого ограничения есть скалярное произведение на ^{[ требуется ссылка ]} ${\displaystyle M}$ ${\displaystyle g:TM\times TM\to \mathbb {R} ,}$ ${\displaystyle x\in M}$ ${\displaystyle g_{x}:T_{x}M\times T_{x}M\to \mathbb {R} }$ ${\displaystyle T_{x}M.}$
• Сильная риманова метрика на — это слабая риманова метрика, которая индуцирует топологию на . Если — сильная риманова метрика, то должно быть гильбертовым многообразием. ^{[ необходима цитата ]} ${\displaystyle M}$ ${\displaystyle g_{x}}$ ${\displaystyle T_{x}M}$ ${\displaystyle g}$ ${\displaystyle M}$

Примеры

• Если — гильбертово пространство , то для любого можно отождествить с Метрика для всех — сильная риманова метрика. ^{[ необходима цитата ]} ${\displaystyle (H,\langle \,\cdot ,\cdot \,\rangle )}$ ${\displaystyle x\in H,}$ ${\displaystyle H}$ ${\displaystyle T_{x}H.}$ ${\displaystyle g_{x}(u,v)=\langle u,v\rangle }$ ${\displaystyle x,u,v\in H}$
• Пусть будет компактным римановым многообразием и обозначим его группу диффеоморфизмов. Последнее является гладким многообразием ( см. здесь ) и фактически группой Ли . ^{[ требуется ссылка ]} Его касательное расслоение в единице является множеством гладких векторных полей на ^{[ требуется ссылка ]} Пусть будет формой объема на Слабая риманова метрика на , обозначаемая , определяется следующим образом. Пусть Тогда для , ${\displaystyle (M,g)}$ ${\displaystyle \operatorname {Diff} (M)}$ ${\displaystyle M.}$ ${\displaystyle \mu }$ ${\displaystyle M.}$ ${\displaystyle L^{2}}$ ${\displaystyle \operatorname {Diff} (M)}$ ${\displaystyle G}$ ${\displaystyle f\in \operatorname {Diff} (M),}$ ${\displaystyle u,v\in T_{f}\operatorname {Diff} (M).}$ ${\displaystyle x\in M,u(x)\in T_{f(x)}M}$

  ${\displaystyle G_{f}(u,v)=\int _{M}g_{f(x)}(u(x),v(x))\,d\mu (x)}$. ^{[ необходима ссылка ]}

Структура метрического пространства

Длина кривых и функция расстояния Римана определяются способом, аналогичным конечномерному случаю. Функция расстояния , называемая геодезическим расстоянием , всегда является псевдометрикой (метрикой, которая не разделяет точки), но она может и не быть метрикой. ^[46] В конечномерном случае доказательство того, что функция расстояния Римана разделяет точки, использует существование предкомпактного открытого множества вокруг любой точки. В бесконечном случае открытые множества больше не являются предкомпактными, поэтому доказательство не выполняется. ${\displaystyle d_{g}:M\times M\to [0,\infty )}$ ${\displaystyle d_{g}}$

• Если — сильная риманова метрика на , то разделяет точки (следовательно, является метрикой) и индуцирует исходную топологию. ^{[ необходима цитата ]} ${\displaystyle g}$ ${\displaystyle M}$ ${\displaystyle d_{g}}$
• Если — слабая риманова метрика, может не разделять точки. Фактически, она может быть даже тождественно равна 0. ^[46] Например, если — компактное риманово многообразие, то слабая риманова метрика на индуцирует исчезающее геодезическое расстояние. ^[47] ${\displaystyle g}$ ${\displaystyle d_{g}}$ ${\displaystyle (M,g)}$ ${\displaystyle L^{2}}$ ${\displaystyle \operatorname {Diff} (M)}$

Теорема Хопфа–Ринова

В случае сильных римановых метрик одна часть конечномерного закона Хопфа–Ринова все еще справедлива.

Теорема : Пусть — сильное риманово многообразие. Тогда метрическая полнота (в метрике ) влечет геодезическую полноту. ^{[ требуется ссылка ]} ${\displaystyle (M,g)}$ ${\displaystyle d_{g}}$

Однако геодезически полное сильное риманово многообразие может не быть метрически полным и может иметь замкнутые и ограниченные подмножества, которые не являются компактными. ^{[ требуется ссылка ]} Кроме того, сильное риманово многообразие, для которого все замкнутые и ограниченные подмножества являются компактными, может не быть геодезически полным. ^{[ требуется ссылка ]}

Если — слабая риманова метрика, то ни одно понятие полноты не подразумевает другого в общем случае. ^{[ необходима цитата ]} ${\displaystyle g}$

Смотрите также

• Гладкий коллектор
• Риманова геометрия
• коллектор Финслера
• Субриманово многообразие
• Псевдориманово многообразие
• Метрический тензор
• Эрмитово многообразие
• Симплектическое многообразие
• коллектор Калера
• многообразие Эйнштейна

Ссылки

Примечания

1. ду Карму 1992, стр. 35–36.
2. do Carmo 1992, стр. 37.
3. do Carmo 1992, стр. 38.
4. Lee 2018, стр. 13.
5. Ли 2018, стр. 26.
6. Lee 2018, стр. 12.
7. Lee 2018, стр. 30.
8. Ли 2018, стр. 31.
9. Ли 2018, стр. 12–13.
10. Lee 2018, стр. 15.
11. Ли 2018, стр. 16.
12. Lee 2018, стр. 20.
13. Ли 2018, стр. 11.
14. Ли 2018, стр. 39.
15. Берчер 2015, стр. 276.
16. Ли 2018, стр. 89–91.
17. Ли 2018, стр. 122–123.
18. Ли 2018, стр. 100.
19. Ли 2018, стр. 101–102.
20. Ли 2018, стр. 103.
21. Ли 2018, стр. 103–104.
22. Lee 2018, стр. 105.
23. Ли 2018, стр. 156.
24. Ли 2018, стр. 137.
25. Ли 2018, стр. 131.
26. до Кармо 1992, стр. 146–147.
27. Ли 2018, стр. 105–110.
28. Ли 2018, стр. 201.
29. Ли 2018, стр. 200.
30. Ли 2018, стр. 196–197.
31. Ли 2018, стр. 207.
32. Ли 2018, стр. 210.
33. Wolf 2011, Глава 2.
34. Вольф 2011, Главы 2 и 7.
35. Вольф 2011, Главы 2 и 3.
36. Чигер и Эбин 2008, Предложение 3.18.
37. Чигер и Эбин 2008, Следствие 3.19; Петерсен 2016, Раздел 4.4.
38. Петерсен 2016, раздел 4.4.3 и стр. 399.
39. Петерсен 2016, стр. 369.
40. В модели верхнего полупространства гиперболического пространства структура группы Ли определяется как ${\displaystyle (x_{1},\ldots ,x_{n})\cdot (y_{1},\ldots ,y_{n})=(x_{1}+y_{n}x_{1},\ldots ,x_{n-1}+y_{n}x_{n-1},x_{n}y_{n}).}$
41. Ли 2018, Пример 3.16f.
42. Ли 2018, стр. 72; Милнор 1976.
43. Кобаяши и Номидзу 1963, Теорема IV.4.5.
44. Besse 1987, Раздел 7C.
45. Petersen 2016, Глава 10.
46. Маньяни и Тиберио 2020.
47. Мичор и Мамфорд 2005.

Источники

• Бесс, Артур Л. (1987). Многообразия Эйнштейна . Ergebnisse der Mathematik und ihrer Grenzgebiete (3). Том. 10. Берлин: Springer-Verlag . дои : 10.1007/978-3-540-74311-8. ISBN 3-540-15279-2. MR  0867684. Zbl  0613.53001.
• Чигер, Джефф ; Эбин, Дэвид Г. (2008). Теоремы сравнения в римановой геометрии (переиздание оригинального издания 1975 г.). Провиденс, Род-Айленд: AMS Chelsea Publishing . doi :10.1090/chel/365. ISBN 978-0-8218-4417-5. MR  2394158. Zbl  1142.53003.
• ду Карму, Манфредо Пердигао (1992). Риманова геометрия . Математика: теория и приложения (Перевод со второго португальского издания 1979 г. оригинального издания). Бостон, Массачусетс: Birkhäuser Boston . ISBN 978-0-8176-3490-2. MR  1138207. Zbl  0752.53001.
• Громов, Миша (1999). Метрические структуры для римановых и неримановых пространств . Прогресс в математике. Т. 152. Перевод Бейтса, Шона Майкла. С приложениями М. Каца , П. Пансу и С. Семмеса . (На основе оригинального французского издания 1981 г.). Бостон, Массачусетс: Birkhäuser Boston, Inc. doi : 10.1007/978-0-8176-4583-0. ISBN 0-8176-3898-9. MR  1699320. Zbl  0953.53002.
• Кобаяси, Сёсити ; Номидзу, Кацуми (1963). Основы дифференциальной геометрии. Том I. Нью-Йорк–Лондон: John Wiley & Sons, Inc. MR  0152974. Zbl  0119.37502.
• Ли, Джон М. (2018). Введение в римановы многообразия . Springer-Verlag . ISBN 978-3-319-91754-2.
• Петерсен, Питер (2016). Риманова геометрия . Graduate Texts in Mathematics . Vol. 171 (Третье издание 1998 г., оригинальное издание). Springer, Cham . doi :10.1007/978-3-319-26654-1. ISBN 978-3-319-26652-7. MR  3469435. Zbl  1417.53001.
• Вольф, Джозеф А. (2011). Пространства постоянной кривизны (Шестое издание оригинального издания 1967 года). Провиденс, Род-Айленд: AMS Chelsea Publishing . doi :10.1090/chel/372. ISBN 978-0-8218-5282-8. MR  2742530. Zbl  1216.53003.
• Burtscher, Annegret (2015). «Структуры длины на многообразиях с непрерывными римановыми метриками». New York Journal of Mathematics . 21 : 273–296. ISSN  1076-9803.
• Маньяни, Валентино; Тиберио, Даниэле (2020). «Замечание об исчезающих геодезических расстояниях в бесконечных измерениях». Proc. Amer. Math. Soc . 148 (1): 3653–3656. arXiv : 1910.06430 . doi :10.1090/proc/14986. S2CID  204578276.
• Michor, Peter W.; Mumford, David (2005). «Исчезающее геодезическое расстояние на пространствах подмногообразий и диффеоморфизмов». Documenta Math . 10 : 217–245. arXiv : math/0409303 . doi :10.4171/dm/187. S2CID  69260.
• Милнор, Джон (1976). «Кривизны левоинвариантных метрик на группах Ли». Advances in Mathematics . 21 (3): 293–329. doi : 10.1016/S0001-8708(76)80002-3 . MR  0425012. Zbl  0341.53030.

Внешние ссылки

• Л.А. Сидоров (2001) [1994], "Риманова метрика", Энциклопедия математики , Издательство ЭМС