Волновая функция

Математическое описание квантового состояния

Сравнение классических и квантовых концепций гармонического осциллятора для одной бесспиновой частицы. Эти два процесса сильно различаются. Классический процесс (A–B) представлен как движение частицы по траектории. Квантовый процесс (C–H) не имеет такой траектории. Вместо этого он представлен как волна; здесь вертикальная ось показывает действительную часть (синюю) и мнимую часть (красную) волновой функции. Панели (C–F) показывают четыре различных решения уравнения Шредингера в виде стоячей волны . Панели (G–H) далее показывают две различные волновые функции, которые являются решениями уравнения Шредингера, но не стоячими волнами.

Волновая функция изначально сильно локализованной свободной частицы.

В квантовой физике волновая функция ( или волновая функция ) — это математическое описание квантового состояния изолированной квантовой системы . Наиболее распространенными символами для волновой функции являются греческие буквы ψ и Ψ (строчная и заглавная psi соответственно). Волновые функции являются комплекснозначными . Например, волновая функция может назначать комплексное число каждой точке в области пространства. Правило Борна ^{[1] [2] [3]} предоставляет средства для превращения этих комплексных амплитуд вероятности в фактические вероятности. В одной общей форме оно гласит, что квадрат модуля волновой функции, зависящий от положения, является плотностью вероятности измерения частицы как находящейся в данном месте. Интеграл квадрата модуля волновой функции по всем степеням свободы системы должен быть равен 1, условие, называемое нормализацией . Поскольку волновая функция является комплекснозначной, можно измерить только ее относительную фазу и относительную величину; ее значение само по себе ничего не говорит о величинах или направлениях измеряемых наблюдаемых. Необходимо применить к волновой функции ψ квантовые операторы , собственные значения которых соответствуют множествам возможных результатов измерений, и вычислить статистические распределения для измеряемых величин.

Волновые функции могут быть функциями переменных, отличных от положения, например импульса . Информация, представленная волновой функцией, зависящей от положения, может быть преобразована в волновую функцию, зависящую от импульса, и наоборот, с помощью преобразования Фурье . Некоторые частицы, такие как электроны и фотоны , имеют ненулевой спин , и волновая функция для таких частиц включает спин как внутреннюю дискретную степень свободы; могут быть включены и другие дискретные переменные, такие как изоспин . Когда система имеет внутренние степени свободы, волновая функция в каждой точке непрерывных степеней свободы (например, точка в пространстве) назначает комплексное число для каждого возможного значения дискретных степеней свободы (например, z-компонента спина). Эти значения часто отображаются в матрице столбцов (например, вектор-столбец 2 × 1 для нерелятивистского электрона со спином 1 ⁄ 2 ).

Согласно принципу суперпозиции квантовой механики, волновые функции можно складывать и умножать на комплексные числа, чтобы сформировать новые волновые функции и образовать гильбертово пространство . Внутреннее произведение между двумя волновыми функциями является мерой перекрытия между соответствующими физическими состояниями и используется в основополагающей вероятностной интерпретации квантовой механики, правиле Борна , связывающем вероятности перехода с внутренними произведениями. Уравнение Шредингера определяет, как волновые функции развиваются с течением времени, и волновая функция ведет себя качественно как другие волны , такие как волны на воде или волны на струне, потому что уравнение Шредингера математически является типом волнового уравнения . Это объясняет название «волновая функция» и приводит к дуализму волна–частица . Однако волновая функция в квантовой механике описывает своего рода физическое явление, по состоянию на 2023 год все еще открытое для различных интерпретаций , которое принципиально отличается от классических механических волн. ^{[4] [5] [6] [7] [8] [9] [10]}

Историческая справка

В 1900 году Макс Планк постулировал пропорциональность между частотой фотона и его энергией , , ^{[11] [12] а в 1916 году соответствующее соотношение между} импульсом фотона и длиной волны , , ^[13] где - постоянная Планка . В 1923 году Де Бройль был первым, кто предположил, что соотношение , теперь называемое соотношением Де Бройля , справедливо для массивных частиц, главным ключом к этому является инвариантность Лоренца , ^[14] и это можно рассматривать как отправную точку для современного развития квантовой механики. Уравнения представляют дуализм волна-частица как для безмассовых, так и для массивных частиц. ${\displaystyle f}$ ${\displaystyle E}$ ${\displaystyle E=hf}$ ${\displaystyle p}$ ${\displaystyle \lambda }$ ${\displaystyle \lambda ={\frac {h}{p}}}$ ${\displaystyle h}$ ${\displaystyle \lambda ={\frac {h}{p}}}$

В 1920-х и 1930-х годах квантовая механика была разработана с использованием исчисления и линейной алгебры . Среди тех, кто использовал методы исчисления, были Луи де Бройль , Эрвин Шредингер и другие, разработавшие « волновую механику ». Среди тех, кто применял методы линейной алгебры, были Вернер Гейзенберг , Макс Борн и другие, разработавшие « матричную механику ». Впоследствии Шредингер показал, что эти два подхода эквивалентны. ^[15]

В 1926 году Шредингер опубликовал знаменитое волновое уравнение, теперь названное в его честь, уравнение Шредингера . Это уравнение было основано на классическом законе сохранения энергии с использованием квантовых операторов и соотношений де Бройля, а решения уравнения являются волновыми функциями для квантовой системы. ^[16] Однако никто не понимал, как его интерпретировать. ^[17] Сначала Шредингер и другие думали, что волновые функции представляют собой частицы, которые рассеяны, причем большая часть частицы находится там, где волновая функция велика. ^[18] Было показано, что это несовместимо с упругим рассеянием волнового пакета (представляющего частицу) от цели; он распространяется во всех направлениях. ^[1] Хотя рассеянная частица может рассеиваться в любом направлении, она не распадается и не разлетается во всех направлениях. В 1926 году Борн представил перспективу амплитуды вероятности . ^{[1] [2] [19]} Это напрямую связывает вычисления квантовой механики с вероятностными экспериментальными наблюдениями. Он принят как часть Копенгагенской интерпретации квантовой механики. Существует много других интерпретаций квантовой механики . В 1927 году Хартри и Фок сделали первый шаг в попытке решить волновую функцию N -тела и разработали цикл самосогласования : итерационный алгоритм для приближения решения. Теперь он также известен как метод Хартри–Фока . ^[20] Определитель Слейтера и перманент (матрицы ) были частью метода, предоставленного Джоном С. Слейтером .

Шредингер действительно столкнулся с уравнением для волновой функции, которое удовлетворяло релятивистскому закону сохранения энергии , прежде чем он опубликовал нерелятивистское, но отбросил его, поскольку оно предсказывало отрицательные вероятности и отрицательные энергии . В 1927 году Клейн , Гордон и Фок также нашли его, но включили электромагнитное взаимодействие и доказали, что оно инвариантно относительно Лоренца . Де Бройль также пришел к тому же уравнению в 1928 году. Это релятивистское волновое уравнение теперь наиболее известно как уравнение Клейна–Гордона . ^[21]

В 1927 году Паули феноменологически нашел нерелятивистское уравнение для описания частиц со спином 1/2 в электромагнитных полях, теперь называемое уравнением Паули . ^[22] Паули обнаружил, что волновая функция не описывается одной комплексной функцией пространства и времени, а нуждается в двух комплексных числах, которые соответственно соответствуют спиновым состояниям +1/2 и −1/2 фермиона. Вскоре после этого в 1928 году Дирак нашел уравнение из первого успешного объединения специальной теории относительности и квантовой механики, примененное к электрону , теперь называемое уравнением Дирака . В нем волновая функция представляет собой спинор, представленный четырьмя комплекснозначными компонентами: ^{[20] двумя для электрона и двумя для} античастицы электрона , позитрона . В нерелятивистском пределе волновая функция Дирака напоминает волновую функцию Паули для электрона. Позже были найдены другие релятивистские волновые уравнения .

Волновые функции и волновые уравнения в современных теориях

Все эти волновые уравнения имеют непреходящее значение. Уравнение Шредингера и уравнение Паули во многих обстоятельствах являются превосходными приближениями релятивистских вариантов. Их значительно легче решать в практических задачах, чем релятивистские аналоги.

Уравнение Клейна–Гордона и уравнение Дирака , хотя и являются релятивистскими, не представляют собой полного примирения квантовой механики и специальной теории относительности. Раздел квантовой механики, где эти уравнения изучаются так же, как уравнение Шредингера, часто называемый релятивистской квантовой механикой , хотя и весьма успешен, имеет свои ограничения (см., например, сдвиг Лэмба ) и концептуальные проблемы (см., например, море Дирака ).

Относительность делает неизбежным, что число частиц в системе не является постоянным. Для полного согласования необходима квантовая теория поля . ^[23] В этой теории волновые уравнения и волновые функции имеют свое место, но в несколько ином обличье. Главными объектами интереса являются не волновые функции, а операторы, так называемые операторы поля (или просто поля, где подразумевается «оператор») в гильбертовом пространстве состояний (описание будет дано в следующем разделе). Оказывается, что исходные релятивистские волновые уравнения и их решения по-прежнему необходимы для построения гильбертова пространства. Более того, свободные операторы полей , т. е. когда предполагается, что взаимодействия не существуют, оказываются (формально) удовлетворяющими тому же уравнению, что и поля (волновые функции) во многих случаях.

Таким образом, уравнение Клейна–Гордона (спин 0 ) и уравнение Дирака (спин 1 ⁄ 2 ) в этом виде остаются в теории. Аналоги с более высоким спином включают уравнение Прока (спин 1 ), уравнение Рариты–Швингера (спин 3 ⁄ 2 ) и, в более общем смысле, уравнения Баргмана–Вигнера . Для безмассовых свободных полей двумя примерами являются уравнение Максвелла для свободного поля (спин 1 ) и уравнение Эйнштейна для свободного поля (спин 2 ) для операторов поля. ^[24] Все они по сути являются прямым следствием требования инвариантности Лоренца . Их решения должны преобразовываться при преобразовании Лоренца предписанным образом, т. е. при определенном представлении группы Лоренца , и этого вместе с несколькими другими разумными требованиями, например, свойством разложения кластера , ^[25] с последствиями для причинности достаточно, чтобы исправить уравнения.

Это относится к уравнениям свободного поля; взаимодействия не включены. Если доступна плотность Лагранжа (включая взаимодействия), то формализм Лагранжа даст уравнение движения на классическом уровне. Это уравнение может быть очень сложным и не поддаваться решению. Любое решение будет относиться к фиксированному числу частиц и не будет учитывать термин «взаимодействие», как он упоминается в этих теориях, который включает в себя создание и уничтожение частиц, а не внешние потенциалы, как в обычной «первоквантованной» квантовой теории.

В теории струн ситуация остается аналогичной. Например, волновая функция в импульсном пространстве играет роль коэффициента разложения Фурье в общем состоянии частицы (струны) с импульсом, который не является четко определенным. ^[26]

Определение (одна бесспиновая частица в одном измерении)

Действительные части волновой функции положения Ψ( x ) и волновой функции импульса Φ( p ) , и соответствующие плотности вероятности |Ψ( x )| ² и |Φ( p )| ² , для одной частицы со спином 0 в одном измерении x или p . Цветовая непрозрачность частиц соответствует плотности вероятности ( а не волновой функции) нахождения частицы в положении x или импульсе p .

На данный момент рассмотрим простой случай нерелятивистской одиночной частицы без спина в одном пространственном измерении. Более общие случаи обсуждаются ниже.

Согласно постулатам квантовой механики , состояние физической системы в фиксированный момент времени задается волновой функцией, принадлежащей сепарабельному комплексному гильбертову пространству . ^{[27] [28]} Таким образом, внутреннее произведение двух волновых функций Ψ ₁ и Ψ ₂ можно определить как комплексное число (в момент времени t ) ^{[nb 1]} ${\displaystyle t}$

${\displaystyle (\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty }$.

Более подробно об этом ниже. Однако внутреннее произведение волновой функции Ψ на саму себя,

${\displaystyle (\Psi ,\Psi )=\|\Psi \|^{2}}$,

всегда является положительным действительным числом. Число ‖ Ψ ‖ (не ‖ Ψ ‖ ² ) называется нормой волновой функции Ψ . Рассматриваемое сепарабельное гильбертово пространство бесконечномерно , ^{[nb 2]} что означает, что не существует конечного набора квадратично интегрируемых функций , которые можно было бы складывать в различных комбинациях для создания всех возможных квадратично интегрируемых функций .

Волновые функции позиционного пространства

Состояние такой частицы полностью описывается ее волновой функцией, где x — положение, а t — время. Это комплекснозначная функция двух действительных переменных x и t . $${\displaystyle \Psi (x,t)\,,}$$

Для одной бесспиновой частицы в одном измерении, если волновая функция интерпретируется как амплитуда вероятности ; квадрат модуля волновой функции, положительное действительное число интерпретируется как плотность вероятности для измерения положения частицы в заданное время t . Звездочка указывает на комплексное сопряжение . Если положение частицы измеряется , ее местоположение не может быть определено из волновой функции, но описывается распределением вероятностей . $${\displaystyle \left|\Psi (x,t)\right|^{2}=\Psi ^{*}(x,t)\Psi (x,t)=\rho (x),}$$

Условие нормализации

Вероятность того, что ее положение x будет в интервале a ≤ x ≤ b, является интегралом плотности по этому интервалу: где t — время, в которое была измерена частица. Это приводит к условию нормировки : поскольку если частица измерена, то существует 100% вероятность того, что она будет где-то . $${\displaystyle P_{a\leq x\leq b}(t)=\int _{a}^{b}\,|\Psi (x,t)|^{2}dx}$$ $${\displaystyle \int _{-\infty }^{\infty }\,|\Psi (x,t)|^{2}dx=1\,,}$$

Для данной системы множество всех возможных нормализуемых волновых функций (в любой момент времени) образует абстрактное математическое векторное пространство , что означает, что можно складывать различные волновые функции и умножать волновые функции на комплексные числа. Технически волновые функции образуют луч в проективном гильбертовом пространстве, а не в обычном векторном пространстве.

Квантовые состояния как векторы

В определенный момент времени все значения волновой функции Ψ( x , t ) являются компонентами вектора. Их несчетно бесконечно много, и вместо суммирования используется интегрирование. В нотации Бракета этот вектор записывается и называется «вектором квантового состояния» или просто «квантовым состоянием». Понимание волновых функций как элементов абстрактного векторного пространства имеет несколько преимуществ: $${\displaystyle |\Psi (t)\rangle =\int \Psi (x,t)|x\rangle dx}$$

• Все мощные инструменты линейной алгебры могут быть использованы для манипулирования и понимания волновых функций. Например:
  • Линейная алгебра объясняет, как векторному пространству можно задать базис , и тогда любой вектор в векторном пространстве можно выразить в этом базисе. Это объясняет связь между волновой функцией в пространстве положений и волновой функцией в пространстве импульсов и предполагает, что существуют и другие возможности.
  • Обозначение Бракета можно использовать для манипулирования волновыми функциями.
• Идея о том, что квантовые состояния являются векторами в абстрактном векторном пространстве, является абсолютно общей для всех аспектов квантовой механики и квантовой теории поля , тогда как идея о том, что квантовые состояния являются комплекснозначными «волновыми» функциями пространства, верна только в определенных ситуациях.

Параметр времени часто опускается, и будет в следующем. Координата x является непрерывным индексом. Векторы | x ⟩ называются несобственными , которые, в отличие от собственных векторов , нормируемых к единице, могут быть нормализованы только к дельта-функции Дирака. ^{[nb 3] [nb 4] [29]} таким образом , и что проливает свет на оператор тождества , который аналогичен отношению полноты ортонормированного базиса в N-мерном гильбертовом пространстве. $${\displaystyle \langle x'|x\rangle =\delta (x'-x)}$$ $${\displaystyle \langle x'|\Psi \rangle =\int \Psi (x)\langle x'|x\rangle dx=\Psi (x')}$$ $${\displaystyle |\Psi \rangle =\int |x\rangle \langle x|\Psi \rangle dx=\left(\int |x\rangle \langle x|dx\right)|\Psi \rangle }$$ $${\displaystyle I=\int |x\rangle \langle x|dx\,.}$$

Нахождение оператора тождества в базисе позволяет явно выразить абстрактное состояние в базисе и даже больше (скалярное произведение между двумя векторами состояния и другие операторы для наблюдаемых могут быть выражены в базисе).

Волновые функции импульсно-пространственного пространства

Частица также имеет волновую функцию в импульсном пространстве : где p — импульс в одном измерении, который может иметь любое значение от −∞ до +∞ , а t — время. $${\displaystyle \Phi (p,t)}$$

Аналогично случаю положения, внутреннее произведение двух волновых функций Φ ₁ ( p , t ) и Φ ₂ ( p , t ) можно определить как: $${\displaystyle (\Phi _{1},\Phi _{2})=\int _{-\infty }^{\infty }\,\Phi _{1}^{*}(p,t)\Phi _{2}(p,t)dp\,.}$$

Одним из частных решений уравнения Шредингера, не зависящего от времени, является плоская волна , которую можно использовать для описания частицы с импульсом, равным p , поскольку она является собственной функцией оператора импульса. Эти функции не нормализуются до единицы (они не интегрируются с квадратом), поэтому они не являются элементами физического гильбертова пространства. Набор образует то, что называется базисом импульса . Этот «базис» не является базисом в обычном математическом смысле. Во-первых, поскольку функции не нормализуются, они вместо этого нормализуются до дельта-функции , ^{[nb 4]} $${\displaystyle \Psi _{p}(x)=e^{ipx/\hbar },}$$ $${\displaystyle \{\Psi _{p}(x,t),-\infty \leq p\leq \infty \}}$$ $${\displaystyle (\Psi _{p},\Psi _{p'})=\delta (p-p').}$$

Во-вторых, хотя они линейно независимы, их слишком много (они образуют несчетное множество) для основы физического гильбертова пространства. Их все еще можно использовать для выражения всех функций в нем с помощью преобразований Фурье, как описано далее.

Отношения между представлениями положения и импульса

Представления x и p следующие: $${\displaystyle {\begin{aligned}|\Psi \rangle =I|\Psi \rangle &=\int |x\rangle \langle x|\Psi \rangle dx=\int \Psi (x)|x\rangle dx,\\|\Psi \rangle =I|\Psi \rangle &=\int |p\rangle \langle p|\Psi \rangle dp=\int \Phi (p)|p\rangle dp.\end{aligned}}}$$

Теперь возьмем проекцию состояния Ψ на собственные функции импульса, используя последнее выражение в двух уравнениях, $${\displaystyle \int \Psi (x)\langle p|x\rangle dx=\int \Phi (p')\langle p|p'\rangle dp'=\int \Phi (p')\delta (p-p')dp'=\Phi (p).}$$

Затем, используя известное выражение для соответствующим образом нормализованных собственных состояний импульса в решениях позиционного представления свободного уравнения Шредингера, получаем $${\displaystyle \langle x|p\rangle =p(x)={\frac {1}{\sqrt {2\pi \hbar }}}e^{{\frac {i}{\hbar }}px}\Rightarrow \langle p|x\rangle ={\frac {1}{\sqrt {2\pi \hbar }}}e^{-{\frac {i}{\hbar }}px},}$$ $${\displaystyle \Phi (p)={\frac {1}{\sqrt {2\pi \hbar }}}\int \Psi (x)e^{-{\frac {i}{\hbar }}px}dx\,.}$$

Аналогично, используя собственные функции положения, $${\displaystyle \Psi (x)={\frac {1}{\sqrt {2\pi \hbar }}}\int \Phi (p)e^{{\frac {i}{\hbar }}px}dp\,.}$$

Таким образом, обнаружено, что волновые функции пространства положения и пространства импульса являются преобразованиями Фурье друг друга. ^[30] Это два представления одного и того же состояния, содержащие одну и ту же информацию, и любого из них достаточно для вычисления любого свойства частицы.

На практике волновая функция пространства положения используется гораздо чаще , чем волновая функция пространства импульса. Потенциал, входящий в соответствующее уравнение (Шредингера, Дирака и т. д.), определяет, в каком базисе описание будет проще всего. Для гармонического осциллятора x и p входят симметрично, поэтому не имеет значения, какое описание используется. Получается то же самое уравнение (по модулю констант). Из этого, с небольшими домыслами, следует, что решения волнового уравнения гармонического осциллятора являются собственными функциями преобразования Фурье в L ² . ^{[nb 5]}

Определения (другие случаи)

Ниже приведены общие формы волновой функции для систем в более высоких измерениях и с большим количеством частиц, а также включающие другие степени свободы, помимо координат положения или компонентов импульса.

Конечномерное гильбертово пространство

Хотя гильбертовы пространства изначально относятся к бесконечномерным полным внутренним пространствам, они, по определению, включают в себя также конечномерные полные внутренние пространства . ^[31] В физике их часто называют конечномерными гильбертовыми пространствами . ^[32] Для каждого конечномерного гильбертова пространства существуют ортонормированные базисные кеты, которые охватывают все гильбертово пространство.

Если N -мерное множество ортонормально, то оператор проекции для пространства, охватываемого этими состояниями, определяется выражением: ${\textstyle \{|\phi _{i}\rangle \}}$

$${\displaystyle P=\sum _{i}|\phi _{i}\rangle \langle \phi _{i}|=I}$$где проекция эквивалентна оператору тождества, поскольку охватывает все гильбертово пространство, таким образом оставляя любой вектор из гильбертова пространства неизменным. Это также известно как отношение полноты конечномерного гильбертова пространства. ${\textstyle \{|\phi _{i}\rangle \}}$

Вместо этого волновая функция задается следующим образом:

$${\displaystyle |\psi \rangle =I|\psi \rangle =\sum _{i}|\phi _{i}\rangle \langle \phi _{i}|\psi \rangle }$$где , — набор комплексных чисел, которые можно использовать для построения волновой функции с использованием приведенной выше формулы. ${\textstyle \{\langle \phi _{i}|\psi \rangle \}}$

Вероятностная интерпретация внутреннего продукта

Если набор представляет собой собственные числа невырожденной наблюдаемой с собственными значениями , то согласно постулатам квантовой механики вероятность измерения наблюдаемой определяется по правилу Борна как: [ ^33] ${\textstyle \{|\phi _{i}\rangle \}}$ ${\textstyle \lambda _{i}}$ ${\textstyle \lambda _{i}}$

$${\displaystyle P_{\psi }(\lambda _{i})=|\langle \phi _{i}|\psi \rangle |^{2}}$$

Для невырожденности некоторой наблюдаемой, если собственные значения имеют подмножество собственных векторов, обозначенных как , согласно постулатам квантовой механики , вероятность измерения наблюдаемой определяется по формуле: ${\textstyle \{|\phi _{i}\rangle \}}$ ${\textstyle \lambda }$ ${\textstyle \{|\lambda ^{(j)}\rangle \}}$ ${\textstyle \lambda _{i}}$

$${\displaystyle P_{\psi }(\lambda )=\sum _{j}|\langle \lambda ^{(j)}|\psi \rangle |^{2}=|{\widehat {P}}_{\lambda }|\psi \rangle |^{2}}$$где — оператор проекции состояний на подпространство, охватываемое . Равенство следует из ортогональной природы . ${\textstyle {\widehat {P}}_{\lambda }=\sum _{j}|\lambda ^{(j)}\rangle \langle \lambda ^{(j)}|}$ ${\textstyle \{|\lambda ^{(j)}\rangle \}}$ ${\textstyle \{|\phi _{i}\rangle \}}$

Следовательно, которые определяют состояние квантово-механической системы, имеют величины, квадрат которых дает вероятность измерения соответствующего состояния. ${\textstyle \{\langle \phi _{i}|\psi \rangle \}}$ ${\textstyle |\phi _{i}\rangle }$

Физическое значение относительной фазы

В то время как относительная фаза имеет наблюдаемые эффекты в экспериментах, глобальная фаза системы экспериментально неразличима. Например, в частице в суперпозиции двух состояний глобальная фаза частицы не может быть различена путем нахождения ожидаемого значения наблюдаемого или вероятностей наблюдения различных состояний, но относительные фазы могут влиять на ожидаемые значения наблюдаемых.

В то время как общая фаза системы считается произвольной, относительная фаза для каждого состояния подготовленного состояния в суперпозиции может быть определена на основе физического смысла подготовленного состояния и его симметрии. Например, построение спиновых состояний вдоль направления x как суперпозиции спиновых состояний вдоль направления z может быть выполнено путем применения соответствующего преобразования вращения к спиновым состояниям вдоль z, что обеспечивает соответствующую фазу состояний относительно друг друга. ${\textstyle |\phi _{i}\rangle }$

Заявка на включение спина

Пример конечномерного гильбертова пространства может быть построен с использованием спиновых собственных элементов -спиновых частиц, что образует размерное гильбертово пространство . Однако общая волновая функция частицы, которая полностью описывает ее состояние, всегда происходит из бесконечномерного гильбертова пространства , поскольку она включает тензорное произведение с гильбертовым пространством, относящееся к положению или импульсу частицы. Тем не менее, методы, разработанные для конечномерного гильбертова пространства, полезны, поскольку их можно либо рассматривать независимо, либо рассматривать с учетом линейности тензорного произведения. ${\textstyle s}$ ${\textstyle 2s+1}$

Поскольку оператор спина для заданной -спиновой частицы может быть представлен в виде конечной матрицы , которая действует на независимые компоненты вектора спина, обычно предпочтительнее обозначать компоненты спина, используя обозначения матрицы/столбца/строки, где это применимо. ${\textstyle s}$ ${\textstyle (2s+1)^{2}}$ ${\textstyle 2s+1}$

Например, каждый | s _z ⟩ обычно идентифицируется как вектор-столбец: $${\displaystyle |s\rangle \leftrightarrow {\begin{bmatrix}1\\0\\\vdots \\0\\0\\\end{bmatrix}}\,,\quad |s-1\rangle \leftrightarrow {\begin{bmatrix}0\\1\\\vdots \\0\\0\\\end{bmatrix}}\,,\ldots \,,\quad |-(s-1)\rangle \leftrightarrow {\begin{bmatrix}0\\0\\\vdots \\1\\0\\\end{bmatrix}}\,,\quad |-s\rangle \leftrightarrow {\begin{bmatrix}0\\0\\\vdots \\0\\1\\\end{bmatrix}}}$$

но это распространенное злоупотребление обозначениями, поскольку кеты | s _z ⟩ не являются синонимами или эквивалентами векторов-столбцов. Векторы-столбцы просто предоставляют удобный способ выражения спиновых компонентов.

В соответствии с обозначениями оператор спина z-компоненты можно записать как: $${\displaystyle {\frac {1}{\hbar }}{\hat {S}}_{z}={\begin{bmatrix}s&0&\cdots &0&0\\0&s-1&\cdots &0&0\\\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&\cdots &-(s-1)&0\\0&0&\cdots &0&-s\end{bmatrix}}}$$

поскольку собственные векторы оператора спина z-компоненты являются указанными выше векторами-столбцами, а собственные значения являются соответствующими квантовыми числами спина.

Соответственно обозначениям вектор из такого конечномерного гильбертова пространства представляется в виде:

$${\displaystyle |\phi \rangle ={\begin{bmatrix}\langle s|\phi \rangle \\\langle s-1|\phi \rangle \\\vdots \\\langle -(s-1)|\phi \rangle \\\langle -s|\phi \rangle \\\end{bmatrix}}={\begin{bmatrix}\varepsilon _{s}\\\varepsilon _{s-1}\\\vdots \\\varepsilon _{-s+1}\\\varepsilon _{-s}\\\end{bmatrix}}}$$где — соответствующие комплексные числа. ${\textstyle \{\varepsilon _{i}\}}$

В следующем обсуждении, касающемся спина, полная волновая функция рассматривается как тензорное произведение спиновых состояний из конечномерных гильбертовых пространств и волновой функции, которая была разработана ранее. Основой для этого гильбертова пространства, следовательно, считаются: . ${\displaystyle |\mathbf {r} ,s_{z}\rangle =|\mathbf {r} \rangle |s_{z}\rangle }$

Одночастичные состояния в трехмерном позиционном пространстве

Позиционно-пространственная волновая функция одиночной частицы без спина в трех пространственных измерениях похожа на случай одного пространственного измерения выше: где r — вектор положения в трехмерном пространстве, а t — время. Как всегда, Ψ( r ,  t ) — комплекснозначная функция действительных переменных. Как один вектор в нотации Дирака $${\displaystyle \Psi (\mathbf {r} ,t)}$$ $${\displaystyle |\Psi (t)\rangle =\int d^{3}\!\mathbf {r} \,\Psi (\mathbf {r} ,t)\,|\mathbf {r} \rangle }$$

Все предыдущие замечания о внутренних произведениях, волновых функциях пространства импульсов, преобразованиях Фурье и т. д. распространяются на более высокие измерения.

Для частицы со спином , игнорируя позиционные степени свободы, волновая функция является функцией только спина (время является параметром); где s _z — квантовое число проекции спина вдоль оси z . ( Ось z — произвольный выбор; вместо этого можно использовать другие оси, если волновая функция соответствующим образом преобразована, см. ниже.) Параметр s _z , в отличие от r и t , является дискретной переменной . Например, для частицы со спином 1/2 s _z может быть только +1/2 или −1/2 , и не иметь никаких других значений. (В общем случае для спина s , s _z может быть s , s − 1, ..., − s + 1, − s ). Подстановка каждого квантового числа дает комплекснозначную функцию пространства и времени, их 2 s + 1. Их можно расположить в вектор-столбец $${\displaystyle \xi (s_{z},t)}$$

$${\displaystyle \xi ={\begin{bmatrix}\xi (s,t)\\\xi (s-1,t)\\\vdots \\\xi (-(s-1),t)\\\xi (-s,t)\\\end{bmatrix}}=\xi (s,t){\begin{bmatrix}1\\0\\\vdots \\0\\0\\\end{bmatrix}}+\xi (s-1,t){\begin{bmatrix}0\\1\\\vdots \\0\\0\\\end{bmatrix}}+\cdots +\xi (-(s-1),t){\begin{bmatrix}0\\0\\\vdots \\1\\0\\\end{bmatrix}}+\xi (-s,t){\begin{bmatrix}0\\0\\\vdots \\0\\1\\\end{bmatrix}}}$$

В скобочной записи они легко раскладываются в компоненты вектора: $${\displaystyle |\xi (t)\rangle =\sum _{s_{z}=-s}^{s}\xi (s_{z},t)\,|s_{z}\rangle }$$

Весь вектор ξ является решением уравнения Шредингера (с подходящим гамильтонианом), которое разворачивается в связанную систему 2 s + 1 обыкновенных дифференциальных уравнений с решениями ξ ( s , t ), ξ ( s − 1, t ), ..., ξ (− s , t ) . Некоторые авторы используют термин «спиновая функция» вместо «волновая функция». Это противопоставляет решения волновым функциям пространства положения, где координаты положения являются непрерывными степенями свободы, потому что тогда уравнение Шредингера принимает форму волнового уравнения.

В более общем случае для частицы в 3D с любым спином волновая функция может быть записана в «пространстве положения–спин» как: и их также можно организовать в вектор-столбец , в котором спиновая зависимость помещена в индексацию записей, а волновая функция является сложной векторной функцией только пространства и времени. $${\displaystyle \Psi (\mathbf {r} ,s_{z},t)}$$ $${\displaystyle \Psi (\mathbf {r} ,t)={\begin{bmatrix}\Psi (\mathbf {r} ,s,t)\\\Psi (\mathbf {r} ,s-1,t)\\\vdots \\\Psi (\mathbf {r} ,-(s-1),t)\\\Psi (\mathbf {r} ,-s,t)\\\end{bmatrix}}}$$

Все значения волновой функции, не только для дискретных, но и для непрерывных переменных , собираются в один вектор $${\displaystyle |\Psi (t)\rangle =\sum _{s_{z}}\int d^{3}\!\mathbf {r} \,\Psi (\mathbf {r} ,s_{z},t)\,|\mathbf {r} ,s_{z}\rangle }$$

Для одной частицы тензорное произведение ⊗ ее вектора положения-состояния | ψ ⟩ и вектора спинового состояния | ξ ⟩ дает составной вектор положения-спинового состояния с идентификациями $${\displaystyle |\psi (t)\rangle \!\otimes \!|\xi (t)\rangle =\sum _{s_{z}}\int d^{3}\!\mathbf {r} \,\psi (\mathbf {r} ,t)\,\xi (s_{z},t)\,|\mathbf {r} \rangle \!\otimes \!|s_{z}\rangle }$$ $${\displaystyle |\Psi (t)\rangle =|\psi (t)\rangle \!\otimes \!|\xi (t)\rangle }$$ $${\displaystyle \Psi (\mathbf {r} ,s_{z},t)=\psi (\mathbf {r} ,t)\,\xi (s_{z},t)}$$ $${\displaystyle |\mathbf {r} ,s_{z}\rangle =|\mathbf {r} \rangle \!\otimes \!|s_{z}\rangle }$$

Факторизация тензорного произведения собственных энергетических состояний всегда возможна, если орбитальный и спиновый угловые моменты частицы разделимы в операторе Гамильтона, лежащем в основе динамики системы (другими словами, гамильтониан можно разбить на сумму орбитальных и спиновых членов ^[34] ). Зависимость от времени можно поместить в любой из множителей, и временную эволюцию каждого из них можно изучать отдельно. При таких гамильтонианах любое состояние тензорного произведения эволюционирует в другое состояние тензорного произведения, что по сути означает, что любое незапутанное состояние остается незапутанным при временной эволюции. Говорят, что это происходит, когда нет физического взаимодействия между состояниями тензорных произведений. В случае неразделимых гамильтонианов собственные энергетические состояния называются некоторой линейной комбинацией таких состояний, которые не обязательно должны быть факторизуемыми; примерами являются частица в магнитном поле и спин-орбитальная связь .

Предшествующее обсуждение не ограничивается спином как дискретной переменной, может также использоваться полный угловой момент J. ^[35] Другие дискретные степени свободы, такие как изоспин , могут быть выражены аналогично случаю спина выше.

Многочастичные состояния в трехмерном позиционном пространстве

Бегущие волны двух свободных частиц, с подавленными двумя из трех измерений. Сверху — волновая функция в пространстве положений, снизу — волновая функция в пространстве импульсов с соответствующими плотностями вероятности.

Если частиц много, то, как правило, существует только одна волновая функция, а не отдельная волновая функция для каждой частицы. Тот факт, что одна волновая функция описывает много частиц, делает возможными квантовую запутанность и парадокс ЭПР . Волновая функция в позиционном пространстве для N частиц записывается следующим образом: ^[20] где r _i — положение i -й частицы в трехмерном пространстве, а t — время. В целом это комплекснозначная функция 3 N + 1 действительных переменных. $${\displaystyle \Psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},t)}$$

В квантовой механике существует фундаментальное различие между идентичными частицами и различимыми частицами. Например, любые два электрона идентичны и принципиально неотличимы друг от друга; законы физики делают невозможным «нанести идентификационный номер» на определенный электрон, чтобы отслеживать его. ^[30] Это переводится в требование к волновой функции для системы идентичных частиц: где знак + возникает, если все частицы являются бозонами , и знак − , если все они являются фермионами . Другими словами, волновая функция либо полностью симметрична в позициях бозонов, либо полностью антисимметрична в позициях фермионов. ^[36] Физический обмен частицами соответствует математическому переключению аргументов в волновой функции. Свойство антисимметрии фермионных волновых функций приводит к принципу Паули . Как правило, требования бозонной и фермионной симметрии являются проявлением статистики частиц и присутствуют в других формализмах квантового состояния. $${\displaystyle \Psi \left(\ldots \mathbf {r} _{a},\ldots ,\mathbf {r} _{b},\ldots \right)=\pm \Psi \left(\ldots \mathbf {r} _{b},\ldots ,\mathbf {r} _{a},\ldots \right)}$$

Для N различимых частиц (нет двух идентичных , т.е. нет двух с одинаковым набором квантовых чисел) нет требования, чтобы волновая функция была симметричной или антисимметричной.

Для совокупности частиц, некоторые из которых идентичны с координатами r ₁ , r ₂ , ..., а другие различимы x ₁ , x ₂ , ... (не идентичны друг другу и не идентичны вышеупомянутым идентичным частицам), волновая функция симметрична или антисимметрична только относительно идентичных координат частиц r _i : $${\displaystyle \Psi \left(\ldots \mathbf {r} _{a},\ldots ,\mathbf {r} _{b},\ldots ,\mathbf {x} _{1},\mathbf {x} _{2},\ldots \right)=\pm \Psi \left(\ldots \mathbf {r} _{b},\ldots ,\mathbf {r} _{a},\ldots ,\mathbf {x} _{1},\mathbf {x} _{2},\ldots \right)}$$

Опять же, для различимых координат частиц x _i не требуется симметрии .

Волновая функция для N частиц, каждая из которых имеет спин, является комплекснозначной функцией $${\displaystyle \Psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},s_{z\,1},s_{z\,2}\cdots s_{z\,N},t)}$$

Собирая все эти компоненты в единый вектор,

$${\displaystyle |\Psi \rangle =\overbrace {\sum _{s_{z\,1},\ldots ,s_{z\,N}}} ^{\text{discrete labels}}\overbrace {\int _{R_{N}}d^{3}\mathbf {r} _{N}\cdots \int _{R_{1}}d^{3}\mathbf {r} _{1}} ^{\text{continuous labels}}\;\underbrace {{\Psi }(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N},s_{z\,1},\ldots ,s_{z\,N})} _{\begin{array}{c}{\text{wave function (component of }}\\{\text{ state vector along basis state)}}\end{array}}\;\underbrace {|\mathbf {r} _{1},\ldots ,\mathbf {r} _{N},s_{z\,1},\ldots ,s_{z\,N}\rangle } _{\text{basis state (basis ket)}}\,.}$$

Для идентичных частиц требования симметрии применяются как к позиционным, так и к спиновым аргументам волновой функции, поэтому она имеет общую правильную симметрию.

Формулы для внутренних произведений — это интегралы по всем координатам или импульсам и суммы по всем спиновым квантовым числам. Для общего случая N частиц со спином в 3-d это всего N трехмерных объемных интегралов и N сумм по спинам. Дифференциальные объемные элементы d ³ r _i также записываются как " dV _i " или " dx _i dy _i dz _i ". $${\displaystyle (\Psi _{1},\Psi _{2})=\sum _{s_{z\,N}}\cdots \sum _{s_{z\,2}}\sum _{s_{z\,1}}\int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r} _{1}\int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r} _{2}\cdots \int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r} _{N}\Psi _{1}^{*}\left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)\Psi _{2}\left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)}$$

Многомерные преобразования Фурье волновых функций положения или положения-спинового пространства дают волновые функции импульса или импульса-спинового пространства.

Интерпретация вероятности

Для общего случая N частиц со спином в 3d, если Ψ интерпретировать как амплитуду вероятности, плотность вероятности равна $${\displaystyle \rho \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)=\left|\Psi \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)\right|^{2}}$$

и вероятность того, что частица 1 находится в области R ₁ со спином s _{z 1} = m ₁ , а частица 2 находится в области R ₂ со спином s _{z 2} = m ₂ и т.д. в момент времени t, является интегралом плотности вероятности по этим областям и оценивается при этих числах спина:

${\displaystyle P_{\mathbf {r} _{1}\in R_{1},s_{z\,1}=m_{1},\ldots ,\mathbf {r} _{N}\in R_{N},s_{z\,N}=m_{N}}(t)=\int _{R_{1}}d^{3}\mathbf {r} _{1}\int _{R_{2}}d^{3}\mathbf {r} _{2}\cdots \int _{R_{N}}d^{3}\mathbf {r} _{N}\left|\Psi \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},m_{1}\cdots m_{N},t\right)\right|^{2}}$

Физическое значение фазы

В нерелятивистской квантовой механике с помощью волнового уравнения Шредингера, зависящего от времени, можно показать, что уравнение:

$${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {J} =0}$$удовлетворяется, где — плотность вероятности, а , — поток вероятности в соответствии с формой уравнения непрерывности приведенного выше уравнения. ${\textstyle \rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}}$ ${\textstyle \mathbf {J} (\mathbf {x} ,t)={\frac {\hbar }{2im}}(\psi ^{*}\nabla \psi -\psi \nabla \psi ^{*})={\frac {\hbar }{m}}{\text{Im}}(\psi ^{*}\nabla \psi )}$

Используя следующее выражение для волновой функции: где — плотность вероятности, а — фаза волновой функции, можно показать, что: $${\displaystyle \psi (\mathbf {x} ,t)={\sqrt {\rho (\mathbf {x} ,t)}}\exp {\frac {iS(\mathbf {x} ,t)}{\hbar }}}$$ ${\textstyle \rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}}$ ${\textstyle S(\mathbf {x} ,t)}$

$${\displaystyle \mathbf {J} (\mathbf {x} ,t)={\frac {\rho \nabla S}{m}}}$$

Следовательно, пространственное изменение фазы характеризует поток вероятности .

В классической аналогии для величина аналогична скорости. Обратите внимание, что это не подразумевает буквальной интерпретации как скорости, поскольку скорость и положение не могут быть определены одновременно в соответствии с принципом неопределенности . Подставляя форму волновой функции в зависящее от времени волновое уравнение Шредингера и принимая классический предел, : ${\textstyle \mathbf {J} =\rho \mathbf {v} }$ ${\textstyle {\frac {\nabla S}{m}}}$ ${\textstyle {\frac {\nabla S}{m}}}$ ${\textstyle \hbar |\nabla ^{2}S|\ll |\nabla S|^{2}}$

$${\displaystyle {\frac {1}{2m}}|\nabla S(\mathbf {x} ,t)|^{2}+V(\mathbf {x} )+{\frac {\partial S}{\partial t}}=0}$$

Что аналогично уравнению Гамильтона-Якоби из классической механики. Эта интерпретация соответствует теории Гамильтона-Якоби , в которой , где S — главная функция Гамильтона . ^[37] ${\textstyle \mathbf {P} _{\text{class.}}=\nabla S}$

Зависимость от времени

Для систем в не зависящих от времени потенциалах волновая функция всегда может быть записана как функция степеней свободы, умноженная на зависящий от времени фазовый множитель, вид которого задается уравнением Шредингера. Для N частиц, учитывая только их положения и подавляя другие степени свободы, где E — собственное значение энергии системы, соответствующее собственному состоянию Ψ . Волновые функции такого вида называются стационарными состояниями . $${\displaystyle \Psi (\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N},t)=e^{-iEt/\hbar }\,\psi (\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N})\,,}$$

Временная зависимость квантового состояния и операторов может быть размещена в соответствии с унитарными преобразованиями на операторах и состояниях. Для любого квантового состояния |Ψ⟩ и оператора O в картине Шредингера |Ψ( t )⟩ изменяется со временем согласно уравнению Шредингера, в то время как O является постоянным. В картине Гейзенберга все наоборот, |Ψ⟩ является постоянным, в то время как O ( t ) эволюционирует со временем согласно уравнению движения Гейзенберга. Картина Дирака (или взаимодействия) является промежуточной, временная зависимость присутствует как в операторах, так и в состояниях, которые эволюционируют согласно уравнениям движения. Она полезна в первую очередь при вычислении элементов S-матрицы . ^[38]

Нерелятивистские примеры

Ниже приведены решения уравнения Шредингера для одной нерелятивистской бесспиновой частицы.

Конечный потенциальный барьер

Рассеяние на конечном потенциальном барьере высотой V ₀ . Указаны амплитуды и направления левых и правых движущихся волн. Красным цветом обозначены волны, используемые для вывода амплитуды отражения и прохождения. E > V ₀ для этой иллюстрации.

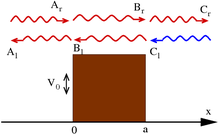
Одной из самых выдающихся особенностей волновой механики является возможность для частицы достичь места с запретительным (в классической механике) потенциалом силы . Распространенной моделью является « потенциальный барьер », одномерный случай имеет потенциал и стационарные решения волнового уравнения имеют вид (для некоторых констант k , κ ) $${\displaystyle V(x)={\begin{cases}V_{0}&|x|<a\\0&|x|\geq a\end{cases}}}$$ $${\displaystyle \Psi (x)={\begin{cases}A_{\mathrm {r} }e^{ikx}+A_{\mathrm {l} }e^{-ikx}&x<-a,\\B_{\mathrm {r} }e^{\kappa x}+B_{\mathrm {l} }e^{-\kappa x}&|x|\leq a,\\C_{\mathrm {r} }e^{ikx}+C_{\mathrm {l} }e^{-ikx}&x>a.\end{cases}}}$$

Обратите внимание, что эти волновые функции не нормированы; см. обсуждение в теории рассеяния .

Стандартная интерпретация этого — как поток частиц, выстреливаемых на шаг слева (направление отрицательного x ): установка A _r = 1 соответствует выстреливанию частиц поодиночке; члены, содержащие A _r и C _r, означают движение вправо, тогда как A _l и C _l — влево. В этой интерпретации пучка положим C _l = 0 , поскольку никакие частицы не приходят справа. Применяя непрерывность волновых функций и их производных на границах, можно определить приведенные выше константы.

3D ограниченные волновые функции электронов в квантовой точке. Здесь показаны прямоугольные и треугольные квантовые точки. Энергетические состояния в прямоугольных точках больше s-типа и p-типа . Однако в треугольной точке волновые функции смешаны из-за симметрии ограничения. (Нажмите для анимации)

В полупроводниковом кристаллите, радиус которого меньше размера его экситонного радиуса Бора , экситоны сжимаются, что приводит к квантовому ограничению . Уровни энергии затем можно моделировать с помощью модели частицы в ящике, в которой энергия различных состояний зависит от длины ящика.

Квантовый гармонический осциллятор

Волновые функции квантового гармонического осциллятора можно выразить через полиномы Эрмита H _n , где n = 0, 1, 2, ... . $${\displaystyle \Psi _{n}(x)={\sqrt {\frac {1}{2^{n}\,n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot e^{-{\frac {m\omega x^{2}}{2\hbar }}}\cdot H_{n}{\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)}}$$

Электронная плотность вероятности для первых нескольких электронных орбиталей атома водорода , показанных в виде сечений. Эти орбитали образуют ортонормальный базис для волновой функции электрона. Различные орбитали изображены в разном масштабе.

Атом водорода

Волновые функции электрона в атоме водорода выражаются через сферические гармоники и обобщенные полиномы Лагерра (они определяются по-разному разными авторами — см. основную статью о них и атоме водорода).

Удобно использовать сферические координаты, и волновую функцию можно разделить на функции каждой координаты, ^[39] где R — радиальные функции, а Y $${\displaystyle \Psi _{n\ell m}(r,\theta ,\phi )=R(r)\,\,Y_{\ell }^{m}\!(\theta ,\phi )}$$^м
_л( θ , φ ) являются сферическими гармониками степени ℓ и порядка m . Это единственный атом, для которого уравнение Шредингера было решено точно. Многоэлектронные атомы требуют приближенных методов. Семейство решений следующее: ^[40] где a ₀ = 4 πε ₀ ħ ² / m _e e ² — радиус Бора , L $${\displaystyle \Psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )}$$^{2 ℓ + 1}
_{n − ℓ − 1}являются обобщенными полиномами Лагерра степени n − ℓ − 1 , n = 1, 2, ... является главным квантовым числом , ℓ = 0, 1, ..., n − 1 азимутальное квантовое число , m = − ℓ , − ℓ + 1, ..., ℓ − 1, ℓ магнитное квантовое число . Водородоподобные атомы имеют очень похожие решения.

Это решение не учитывает спин электрона.

На рисунке водородных орбиталей 19 подизображений являются изображениями волновых функций в пространстве положений (их норма возведена в квадрат). Волновые функции представляют абстрактное состояние, характеризуемое тройкой квантовых чисел ( n , ℓ , m ) в правом нижнем углу каждого изображения. Это главное квантовое число, квантовое число орбитального углового момента и магнитное квантовое число. Вместе с одним квантовым числом проекции спина электрона это полный набор наблюдаемых.

Рисунок может служить иллюстрацией некоторых дополнительных свойств функциональных пространств волновых функций.

• В этом случае волновые функции квадратично интегрируемы. Можно изначально взять функциональное пространство как пространство квадратично интегрируемых функций, обычно обозначаемое L 2 .
• Отображенные функции являются решениями уравнения Шредингера. Очевидно, что не каждая функция в L ² удовлетворяет уравнению Шредингера для атома водорода. Таким образом, пространство функций является подпространством L ² .
• Отображаемые функции образуют часть базиса для функционального пространства. Каждой тройке ( n , ℓ , m ) соответствует базисная волновая функция. Если учитывать спин, то для каждой тройки есть две базисные функции. Таким образом, функциональное пространство имеет счетный базис .
• Базисные функции взаимно ортонормальны .

Волновые функции и функциональные пространства

Концепция функциональных пространств естественным образом входит в обсуждение волновых функций. Функциональное пространство — это набор функций, обычно с некоторыми определяющими требованиями к функциям (в данном случае, чтобы они были квадратично интегрируемыми ), иногда с алгебраической структурой на множестве (в данном случае, структурой векторного пространства со скалярным произведением ), вместе с топологией на множестве. Последнее будет редко использоваться здесь, оно необходимо только для получения точного определения того, что означает для подмножества функционального пространства быть замкнутым . Ниже будет сделан вывод, что функциональное пространство волновых функций является гильбертовым пространством . Это наблюдение является основой преобладающей математической формулировки квантовой механики.

Структура векторного пространства

Волновая функция — это элемент функционального пространства, частично характеризуемый следующими конкретными и абстрактными описаниями.

• Уравнение Шредингера линейно. Это означает, что его решения, волновые функции, можно складывать и умножать на скаляры, чтобы получить новое решение. Множество решений уравнения Шредингера представляет собой векторное пространство.
• Принцип суперпозиции квантовой механики. Если Ψ и Φ — два состояния в абстрактном пространстве состояний квантово-механической системы, а a и b — любые два комплексных числа, то a Ψ + b Φ также является допустимым состоянием. (Считается ли нулевой вектор допустимым состоянием («система отсутствует») — вопрос определения. Нулевой вектор в любом случае не описывает состояние вакуума в квантовой теории поля.) Множество допустимых состояний является векторным пространством.

Это сходство, конечно, не случайно. Существуют также различия между пространствами, о которых следует помнить.

Представления

Базисные состояния характеризуются набором квантовых чисел. Это набор собственных значений максимального набора коммутирующих наблюдаемых . Физические наблюдаемые представлены линейными операторами, также называемыми наблюдаемыми, на векторном пространстве. Максимальность означает, что к набору не может быть добавлено никаких дополнительных алгебраически независимых наблюдаемых, которые коммутируют с уже имеющимися. Выбор такого набора можно назвать выбором представления .

• Это постулат квантовой механики, что физически наблюдаемая величина системы, такая как положение, импульс или спин, представлена ​​линейным эрмитовым оператором в пространстве состояний. Возможные результаты измерения величины являются собственными значениями оператора. ^[18] На более глубоком уровне большинство наблюдаемых, возможно, все, возникают как генераторы симметрий . ^{[18] [41] [nb 6]}
• Физическая интерпретация заключается в том, что такой набор представляет то, что может – в теории – одновременно измеряться с произвольной точностью. Соотношение неопределенности Гейзенберга запрещает одновременные точные измерения двух некоммутирующих наблюдаемых.
• Набор не является уникальным. Например, для одночастичной системы это может быть положение и спин z -проекция, ( x , S _z ) , или это может быть импульс и спин y -проекция, ( p , S _y ) . В этом случае оператор, соответствующий положению ( оператор умножения в представлении положения), и оператор, соответствующий импульсу ( дифференциальный оператор в представлении положения), не коммутируют.
• После выбора представления все еще остается произвол. Остается выбрать систему координат. Это может, например, соответствовать выбору осей x , y и z или выбору криволинейных координат , как показано на примере сферических координат, используемых для волновых функций атома водорода. Этот окончательный выбор также фиксирует базис в абстрактном гильбертовом пространстве. Основные состояния помечаются квантовыми числами, соответствующими максимальному набору коммутирующих наблюдаемых и соответствующей системе координат. ^{[nb 7]}

Абстрактные состояния являются «абстрактными» только в том смысле, что не дан произвольный выбор, необходимый для конкретного явного описания. Это то же самое, что сказать, что не дан выбор максимального набора коммутирующих наблюдаемых. Это аналогично векторному пространству без указанного базиса. Волновые функции, соответствующие состоянию, соответственно, не являются уникальными. Эта неоднозначность отражает неоднозначность в выборе максимального набора коммутирующих наблюдаемых. Для одной спиновой частицы в одном измерении конкретному состоянию соответствуют две волновые функции, Ψ( x , S _z ) и Ψ( p , S _y ) , обе описывающие одно и то же состояние.

• Для каждого выбора максимальных коммутирующих наборов наблюдаемых для абстрактного пространства состояний существует соответствующее представление, которое связано с функциональным пространством волновых функций.
• Между всеми этими различными функциональными пространствами и абстрактным пространством состояний существуют соответствия один к одному (здесь без учета нормализации и ненаблюдаемых фазовых факторов), общим знаменателем здесь является конкретное абстрактное состояние. Например, связь между волновыми функциями импульсного и позиционного пространства, описывающими одно и то же состояние, называется преобразованием Фурье .

Каждый выбор представления следует рассматривать как указание уникального функционального пространства, в котором находятся волновые функции, соответствующие этому выбору представления. Это различие лучше всего сохранить, даже если можно утверждать, что два таких функциональных пространства математически равны, например, являясь набором квадратично интегрируемых функций. Тогда можно рассматривать функциональные пространства как две различные копии этого набора.

Внутренний продукт

Существует дополнительная алгебраическая структура векторных пространств волновых функций и абстрактного пространства состояний.

• Физически различные волновые функции интерпретируются как перекрывающиеся в некоторой степени. Система в состоянии Ψ , которая не перекрывается с состоянием Φ, не может быть обнаружена в состоянии Φ при измерении. Но если Φ ₁ , Φ ₂ , … перекрывают Ψ в некоторой степени, есть вероятность, что измерение системы, описываемой Ψ, будет обнаружено в состояниях Φ ₁ , Φ ₂ , … . Также соблюдаются правила отбора . Они обычно формулируются в сохранении некоторых квантовых чисел. Это означает, что определенные процессы, допустимые с некоторых точек зрения (например, сохранение энергии и импульса), не происходят, поскольку начальная и конечная полные волновые функции не перекрываются.
• Математически оказывается, что решения уравнения Шредингера для конкретных потенциалов ортогональны в некотором роде, это обычно описывается интегралом, где m , n — (наборы) индексов (квантовых чисел), маркирующих различные решения, строго положительная функция w называется весовой функцией, а δ _mn — дельта Кронекера . Интегрирование выполняется по всему соответствующему пространству. $${\displaystyle \int \Psi _{m}^{*}\Psi _{n}w\,dV=\delta _{nm},}$$

Это мотивирует введение скалярного произведения в векторном пространстве абстрактных квантовых состояний, совместимого с математическими наблюдениями выше при переходе к представлению. Оно обозначается (Ψ, Φ) или в нотации Бракета ⟨Ψ|Φ⟩ . Оно дает комплексное число. Со скалярным произведением пространство функций является пространством скалярного произведения . Явный вид скалярного произведения (обычно интеграла или суммы интегралов) зависит от выбора представления, но комплексное число (Ψ, Φ) — нет. Большая часть физической интерпретации квантовой механики вытекает из правила Борна . Оно гласит, что вероятность p нахождения при измерении состояния Φ при условии, что система находится в состоянии Ψ, равна , где Φ и Ψ предполагаются нормализованными. Рассмотрим эксперимент по рассеянию . В квантовой теории поля, если Φ _out описывает состояние в «далеком будущем» («out state») после того, как взаимодействия между рассеивающими частицами прекратились, а Ψ _in — «in state» в «далеком прошлом», то величины (Φ _out , Ψ _in ) , где Φ _out и Ψ _in варьируются по полному набору in states и out states соответственно, называются S-матрицей или матрицей рассеяния . Знание ее, по сути, заключается в решении имеющейся теории, по крайней мере, в том, что касается предсказаний. Измеримые величины, такие как скорости распада и сечения рассеяния, вычисляются из S-матрицы. ^[42] $${\displaystyle p=|(\Phi ,\Psi )|^{2},}$$

Гильбертово пространство

Вышеприведенные наблюдения инкапсулируют суть функциональных пространств, элементами которых являются волновые функции. Однако описание еще не завершено. Существует еще одно техническое требование к функциональному пространству, требование полноты , которое позволяет брать пределы последовательностей в функциональном пространстве и быть уверенным, что если предел существует, то он является элементом функционального пространства. Полное пространство внутреннего произведения называется гильбертовым пространством . Свойство полноты имеет решающее значение в продвинутых трактовках и приложениях квантовой механики. Например, существование операторов проекции или ортогональных проекций зависит от полноты пространства. ^[43] Эти операторы проекции, в свою очередь, имеют важное значение для формулировки и доказательства многих полезных теорем, например, спектральной теоремы . Это не очень важно во вводной квантовой механике, а технические подробности и ссылки можно найти в сносках, подобных следующей. ^{[nb 8]} Пространство L ² является гильбертовым пространством со внутренним произведением, представленным позже. Функциональное пространство примера на рисунке является подпространством L ^2. Подпространство гильбертова пространства является гильбертовым пространством, если оно замкнуто.

Подводя итог, можно сказать, что множество всех возможных нормализуемых волновых функций для системы с определенным выбором базиса вместе с нулевым вектором образуют гильбертово пространство.

Не все интересующие нас функции являются элементами некоторого гильбертова пространства, скажем, L ² . Наиболее ярким примером является набор функций e ^{2 πi p · x ⁄ h} . Это плоские волновые решения уравнения Шредингера для свободной частицы, но они не нормализуются, следовательно, не в L ² . Но они, тем не менее, являются фундаментальными для описания. Используя их, можно выразить функции, которые нормализуются с помощью волновых пакетов . Они, в некотором смысле, являются базисом (но не базисом гильбертова пространства или базисом Гамеля ), в котором могут быть выражены интересующие нас волновые функции. Существует также артефакт «нормализация к дельта-функции», который часто используется для удобства обозначений, см. далее. Сами дельта-функции также не являются квадратично интегрируемыми.

Приведенное выше описание функционального пространства, содержащего волновые функции, в основном математически мотивировано. Функциональные пространства, из-за полноты, в определенном смысле очень большие . Не все функции являются реалистичными описаниями любой физической системы. Например, в функциональном пространстве L ² можно найти функцию, которая принимает значение 0 для всех рациональных чисел и - i для иррациональных чисел в интервале [0, 1] . Это квадратично интегрируемо, ^{[nb 9],} но вряд ли может представлять физическое состояние.

Общие гильбертовы пространства

Хотя пространство решений в целом является гильбертовым пространством, существует множество других гильбертовых пространств, которые обычно встречаются в качестве его ингредиентов.

• Квадратично интегрируемые комплекснозначные функции на интервале [0, 2 π ] . Множество { e ^int /2 π , n ∈ Z } является базисом гильбертова пространства, т.е. максимальным ортонормированным множеством.
• Преобразование Фурье переводит функции из указанного выше пространства в элементы l ² ( Z ) , пространства квадратично суммируемых функций Z → C . Последнее пространство является гильбертовым пространством, а преобразование Фурье является изоморфизмом гильбертовых пространств. _[ ^{nb 10]} Его базисом является { ei , i ∈ Z } с ei ₍ j ) = δ _ij , i , j ∈ Z .
• Самый простой пример охватывающих многочленов — пространство квадратично интегрируемых функций на интервале [–1, 1] , для которого многочлены Лежандра являются базисом гильбертова пространства (полный ортонормированный набор).
• Квадратичные интегрируемые функции на единичной сфере S ² являются гильбертовым пространством. Базисными функциями в этом случае являются сферические гармоники . Полиномы Лежандра являются ингредиентами сферических гармоник. Большинство задач с вращательной симметрией будут иметь «одно и то же» (известное) решение относительно этой симметрии, поэтому исходная задача сводится к задаче меньшей размерности.
• Соответствующие полиномы Лагерра появляются в задаче водородной волновой функции после вынесения сферических гармоник за скобки. Они охватывают гильбертово пространство квадратично интегрируемых функций на полубесконечном интервале [0, ∞) .

В более общем плане можно рассмотреть единую трактовку всех полиномиальных решений второго порядка уравнений Штурма–Лиувилля в условиях гильбертова пространства. К ним относятся полиномы Лежандра и Лагерра, а также полиномы Чебышева , полиномы Якоби и полиномы Эрмита . Все они фактически появляются в физических задачах, последние — в гармоническом осцилляторе , и то, что в противном случае является запутанным лабиринтом свойств специальных функций, становится организованным корпусом фактов. Для этого см. Byron & Fuller (1992, Глава 5).

Встречаются также конечномерные гильбертовы пространства. Пространство C ⁿ является гильбертовым пространством размерности n . Скалярное произведение является стандартным скалярным произведением на этих пространствах. В нем находится «спиновая часть» волновой функции отдельной частицы.

• В нерелятивистском описании электрона n = 2 , а полная волновая функция является решением уравнения Паули .
• В соответствующей релятивистской трактовке n = 4 и волновая функция решает уравнение Дирака .

С большим количеством частиц ситуация становится сложнее. Необходимо использовать тензорные произведения и использовать теорию представлений задействованных групп симметрии ( группу вращения и группу Лоренца соответственно), чтобы извлечь из тензорного произведения пространства, в которых находятся (полные) спиновые волновые функции. (Дополнительные проблемы возникают в релятивистском случае, если частицы не свободны. ^[44] См. уравнение Бете–Солпитера .) Соответствующие замечания применимы к концепции изоспина , для которого группа симметрии — SU(2) . Модели ядерных сил шестидесятых годов (все еще полезные сегодня, см. ядерная сила ) использовали группу симметрии SU(3) . В этом случае также часть волновых функций, соответствующих внутренним симметриям, находятся в некоторых C ⁿ или подпространствах тензорных произведений таких пространств.

• В квантовой теории поля базовым пространством Гильберта является пространство Фока . Оно строится из свободных одночастичных состояний, т. е. волновых функций, когда выбирается представление, и может вмещать любое конечное, не обязательно постоянное во времени число частиц. Интересная (или, скорее, поддающаяся обработке ) динамика заключается не в волновых функциях, а в операторах поля , которые являются операторами, действующими в пространстве Фока. Таким образом, картина Гейзенберга является наиболее распространенным выбором (постоянные состояния, изменяющиеся во времени операторы).

Ввиду бесконечномерной природы системы соответствующие математические инструменты являются объектами изучения функционального анализа .

Упрощенное описание

Непрерывность волновой функции и ее первой пространственной производной (в направлении x , координаты y и z не показаны) в некоторый момент времени t .

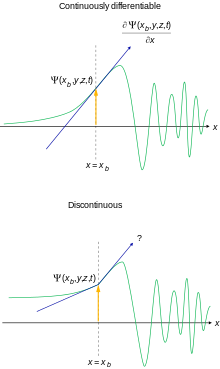
Не все вводные учебники идут долгим путем и вводят полную машину пространства Гильберта, но основное внимание уделяется нерелятивистскому уравнению Шредингера в позиционном представлении для определенных стандартных потенциалов. Следующие ограничения на волновую функцию иногда явно формулируются для того, чтобы вычисления и физическая интерпретация имели смысл: ^{[45] [46]}

• Волновая функция должна быть квадратично интегрируемой . Это мотивировано копенгагенской интерпретацией волновой функции как амплитуды вероятности.
• Он должен быть всюду непрерывным и всюду непрерывно дифференцируемым . Это мотивировано появлением уравнения Шредингера для большинства физически разумных потенциалов.

Можно несколько ослабить эти условия для специальных целей. ^{[nb 11]} Если эти требования не выполняются, то невозможно интерпретировать волновую функцию как амплитуду вероятности. ^[47] Обратите внимание, что исключения из правила непрерывности производных могут возникать в точках бесконечного разрыва потенциального поля. Например, в частице в ящике , где производная волновой функции может быть разрывной на границе ящика, где известно, что потенциал имеет бесконечный разрыв.

Это не изменяет структуру гильбертова пространства, в котором находятся эти конкретные волновые функции, но подпространство квадратично-интегрируемых функций L ² , которое является гильбертовым пространством, удовлетворяющим второму требованию, не замкнуто в L ² , следовательно, само по себе не является гильбертовым пространством. ^{[nb 12]} Функции, которые не удовлетворяют требованиям, по-прежнему необходимы как по техническим, так и по практическим причинам. ^{[nb 13] [nb 14]}

Подробнее о волновых функциях и абстрактном пространстве состояний

Как было показано, набор всех возможных волновых функций в некотором представлении для системы составляет в общем случае бесконечномерное гильбертово пространство. Из-за множественности возможных выборов базиса представления эти гильбертовы пространства не являются уникальными. Поэтому говорят об абстрактном гильбертовом пространстве, пространстве состояний , где выбор представления и базиса остается неопределенным. В частности, каждое состояние представлено как абстрактный вектор в пространстве состояний. ^[48] Квантовое состояние |Ψ⟩ в любом представлении обычно выражается как вектор, где $${\displaystyle |\Psi \rangle =\sum _{\boldsymbol {\alpha }}\int d^{m}\!{\boldsymbol {\omega }}\,\,\Psi ({\boldsymbol {\alpha }},{\boldsymbol {\omega }},t)\,|{\boldsymbol {\alpha }},{\boldsymbol {\omega }}\rangle }$$

• | α , ω ⟩ базисные векторы выбранного представления
• d ^m ω = dω ₁ dω ₂ ... dω _m « дифференциальный элемент объема » в непрерывных степенях свободы
• Ψ( α , ω , t ) — компонент вектора |Ψ⟩ , называемый волновой функцией системы
• α = ( α ₁ , α ₂ , ..., α _n ) безразмерные дискретные квантовые числа
• ω = ( ω ₁ , ω ₂ , ..., ω _m ) непрерывные переменные (не обязательно безразмерные)

Эти квантовые числа индексируют компоненты вектора состояния. Более того, все α находятся в n -мерном множестве A = A ₁ × A ₂ × ... × A _n , где каждое A _i является набором допустимых значений для α _i ; все ω находятся в m -мерном «объеме» Ω ⊆ ℝ ^m , где Ω = Ω ₁ × Ω ₂ × ... × Ω _m , а каждое Ω _i ⊆ R является набором допустимых значений для ω _i , подмножеством действительных чисел R . Для общности n и m не обязательно равны.

Пример:

1. Для одной частицы в 3d со спином s , пренебрегая другими степенями свободы, используя декартовы координаты, мы могли бы взять α = ( s _z ) для спинового квантового числа частицы вдоль направления z и ω = ( x , y , z ) для координат положения частицы. Здесь A = {− s , − s + 1, ..., s − 1, s } — набор разрешенных спиновых квантовых чисел, а Ω = R ³ — набор всех возможных положений частицы во всем 3d позиционном пространстве.
2. Альтернативный выбор — α = ( s _y ) для спинового квантового числа вдоль направления y и ω = ( p _x , p _y , p _z ) для компонент импульса частицы. В этом случае A и Ω такие же, как и раньше.

Плотность вероятности нахождения системы в момент времени в состоянии | α , ω ⟩ равна ${\displaystyle t}$ $${\displaystyle \rho _{\alpha ,\omega }(t)=|\Psi ({\boldsymbol {\alpha }},{\boldsymbol {\omega }},t)|^{2}}$$

Вероятность нахождения системы с α в некоторых или всех возможных дискретно-переменных конфигурациях, D ⊆ A , и ω в некоторых или всех возможных непрерывно-переменных конфигурациях, C ⊆ Ω , является суммой и интегралом по плотности, ^{[nb 15]} $${\displaystyle P(t)=\sum _{{\boldsymbol {\alpha }}\in D}\int _{C}\rho _{\alpha ,\omega }(t)\,\,d^{m}\!{\boldsymbol {\omega }}}$$

Поскольку сумма всех вероятностей должна быть равна 1, условие нормализации должно выполняться в любой момент времени в ходе эволюции системы. $${\displaystyle 1=\sum _{{\boldsymbol {\alpha }}\in A}\int _{\Omega }\rho _{\alpha ,\omega }(t)\,d^{m}\!{\boldsymbol {\omega }}}$$

Условие нормировки требует, чтобы ρ d ^m ω было безразмерным, согласно размерному анализу Ψ должно иметь те же единицы, что и ( ω ₁ ω ₂ ... ω _m ) ^−1/2 .

Онтология

Существует ли волновая функция в реальности и что она собой представляет, являются основными вопросами в интерпретации квантовой механики . Многие известные физики предыдущего поколения ломали голову над этой проблемой, такие как Эрвин Шредингер , Альберт Эйнштейн и Нильс Бор . Некоторые отстаивают формулировки или варианты копенгагенской интерпретации (например, Бор, Юджин Вигнер и Джон фон Нейман ), в то время как другие, такие как Джон Арчибальд Уилер или Эдвин Томпсон Джейнс , придерживаются более классического подхода ^[49] и рассматривают волновую функцию как представление информации в сознании наблюдателя, т. е. меры нашего знания реальности. Некоторые, включая Шредингера, Дэвида Бома и Хью Эверетта III и других, утверждали, что волновая функция должна иметь объективное, физическое существование. Эйнштейн считал, что полное описание физической реальности должно относиться непосредственно к физическому пространству и времени, в отличие от волновой функции, которая относится к абстрактному математическому пространству. ^[50]

Смотрите также

• Бозон
• Теория де Бройля–Бома
• Эксперимент с двумя щелями
• волна Фарадея
• Фермион
• Формулировка фазового пространства
• Уравнение Шредингера
• Коллапс волновой функции
• Волновой пакет

Замечания

1. Здесь предполагается, что функции являются элементами L 2 , пространства квадратично интегрируемых функций. Элементы этого пространства являются, точнее, классами эквивалентности квадратично интегрируемых функций, две функции объявляются эквивалентными, если они различаются на множестве меры Лебега 0 . Это необходимо для получения скалярного произведения (то есть (Ψ, Ψ) = 0 ⇒ Ψ ≡ 0 ) в отличие от полускалярного произведения . Интеграл принимается за интеграл Лебега . Это существенно для полноты пространства, таким образом, давая полное скалярное пространство произведений = Гильбертово пространство.
2. В квантовой механике рассматриваются только сепарабельные гильбертовы пространства , что, используя лемму Цорна , подразумевает, что оно допускает счетно бесконечный базис Шаудера, а не ортонормированный базис в смысле линейной алгебры ( базис Гамеля ).
3. Поскольку технически они не находятся в гильбертовом пространстве. Подробнее см. Спектральную теорему .
4. Также называется «ортонормальностью Дирака», согласно Гриффитсу, Дэвиду Дж. Введение в квантовую механику (3-е изд.).
5. Преобразование Фурье, рассматриваемое как унитарный оператор в пространстве L ^2, имеет собственные значения ±1, ± i . Собственные векторы являются "функциями Эрмита", т.е. полиномами Эрмита , умноженными на гауссову функцию . Описание преобразования Фурье как унитарного преобразования см. в работе Байрона и Фуллера (1992). О собственных значениях и собственных значениях см. в задаче 27 гл. 9.
6. Чтобы это утверждение имело смысл, наблюдаемые должны быть элементами максимального коммутирующего множества. Чтобы увидеть это, просто заметьте, что, например, оператор импульса i-й частицы в системе n частиц не является генератором какой-либо симметрии в природе. С другой стороны, полный импульс является генератором симметрии в природе; трансляционной симметрии.
7. Полученный базис может быть или не быть технически базисом в математическом смысле гильбертовых пространств. Например, состояния определенного положения и определенного импульса не являются квадратично интегрируемыми. Это можно преодолеть с помощью волновых пакетов или путем заключения системы в «ящик». См. дальнейшие замечания ниже.
8. В технических терминах это формулируется следующим образом. Скалярное произведение даёт норму . Эта норма, в свою очередь, индуцирует метрику . Если эта метрика является полной , то вышеупомянутые пределы будут в функциональном пространстве. Тогда скалярное произведение называется полным. Полное скалярное произведение является гильбертовым пространством . Абстрактное пространство состояний всегда берётся как гильбертово пространство. Требование соответствия для функциональных пространств является естественным. Свойство гильбертова пространства абстрактного пространства состояний было первоначально извлечено из наблюдения, что функциональные пространства, образующие нормализуемые решения уравнения Шрёдингера, являются гильбертовыми пространствами.
9. Как поясняется в более поздней сноске, в качестве интеграла следует рассматривать интеграл Лебега , интеграла Римана недостаточно.
10. Conway 1990. Это означает, что внутренние произведения, а значит и нормы, сохраняются, и что отображение является ограниченной, а значит непрерывной, линейной биекцией. Свойство полноты также сохраняется. Таким образом, это правильная концепция изоморфизма в категории гильбертовых пространств.
11. Одной из таких релаксаций является то, что волновая функция должна принадлежать пространству Соболева W ^1,2 . Это означает, что она дифференцируема в смысле распределений , а ее градиент интегрируем с квадратом . Эта релаксация необходима для потенциалов, которые не являются функциями, но являются распределениями, такими как дельта-функция Дирака .
12. Легко визуализировать последовательность функций, удовлетворяющую требованию, которая сходится к разрывной функции. Для этого модифицируйте пример, приведенный в Inner product space#Some examples . Этот элемент, однако, является элементом L ² .
13. Например, в теории возмущений можно построить последовательность функций, приближающих истинную волновую функцию. Эта последовательность будет гарантированно сходиться в большем пространстве, но без предположения о полноценном гильбертовом пространстве не будет гарантировано, что сходимость будет к функции в соответствующем пространстве и, следовательно, решение исходной задачи.
14. Некоторые функции, не являющиеся квадратично интегрируемыми, такие как решения для свободных частиц в виде плоских волн, необходимы для описания, как изложено в предыдущей заметке, а также далее ниже.
15. Здесь: — кратная сумма. $${\displaystyle \sum _{\boldsymbol {\alpha }}\equiv \sum _{\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}}\equiv \sum _{\alpha _{1}}\sum _{\alpha _{2}}\cdots \sum _{\alpha _{n}}}$$

Цитаты

1. Родился в 1926a, переведено в Wheeler & Zurek 1983 на страницах 52–55.
2. Born 1926b, переведено в Ludwig 1968, стр. 206–225. Также здесь Архивировано 2020-12-01 в Wayback Machine .
3. Борн, М. (1954).
4. Родился в 1927 г., стр. 354–357.
5. Гейзенберг 1958, стр. 143.
6. Гейзенберг, В. (1927/1985/2009). Гейзенберг переведен Camilleri 2009, стр. 71 (из Bohr 1985, стр. 142).
7. Мердок 1987, стр. 43.
8. де Бройль 1960, стр. 48.
9. Ландау и Лифшиц 1977, стр. 6.
10. Ньютон 2002, стр. 19–21.
11. "Planck - A very short biography of Planck". spark.iop.org . Institute of Physics . Получено 12 февраля 2023 г. .
12. C/CS Pys C191:Представления и волновые функции 》 1. Соотношение Планка-Эйнштейна E=hv (PDF) . EESC Instructional and Electronics Support, Калифорнийский университет в Беркли . 30 сентября 2008 г. стр. 1 . Получено 12 февраля 2023 г. .
13. Эйнштейн 1916, стр. 47–62, и почти идентичная версия Эйнштейн 1917, стр. 121–128, переведенная в тер Хаар 1967, стр. 167–183.
14. де Бройль 1923, стр. 507–510, 548, 630.
15. Ханле 1977, стр. 606–609.
16. Шредингер 1926, стр. 1049–1070.
17. Типлер, Моска и Фриман 2008.
18. Вайнберг 2013.
19. Янг и Фридман 2008, стр. 1333.
20. Аткинс 1974.
21. Мартин и Шоу 2008.
22. Паули 1927, стр. 601–623.
23. Вайнберг (2002) придерживается точки зрения, что квантовая теория поля выглядит именно так, потому что это единственный способ примирить квантовую механику со специальной теорией относительности.
24. Вайнберг (2002) См. особенно главу 5, где выведены некоторые из этих результатов.
25. Вайнберг 2002 Глава 4.
26. Цвибах 2009.
27. Приложения квантовой механики.
28. Гриффитс 2004, стр. 94.
29. Шанкар 1994, стр. 117.
30. Гриффитс 2004.
31. Тревес 2006, стр. 112-125.
32. Б. Гриффитс, Роберт . «Квантовая механика в гильбертовом пространстве» (PDF) . стр. 1.
33. Ландсман 2009.
34. Шанкар 1994, стр. 378–379.
35. Ландау и Лифшиц 1977.
36. Зеттили 2009, стр. 463.
37. Сакурай, Джун Джон; Наполитано, Джим (2021). Современная квантовая механика (3-е изд.). Кембридж: Cambridge University Press. С. 94–97. ISBN 978-1-108-47322-4.
38. Вайнберг 2002 Глава 3, Матрица рассеяния.
39. Физика для ученых и инженеров – с современной физикой (6-е издание), PA Tipler, G. Mosca, Freeman, 2008, ISBN 0-7167-8964-7 
40. Гриффитс 2008, стр. 162 и далее.
41. Вайнберг 2002.
42. Вайнберг 2002, Глава 3.
43. Конвей 1990.
44. Грейнер и Рейнхардт 2008.
45. Эйсберг и Резник 1985.
46. Рэй 2008.
47. Аткинс 1974, стр. 258.
48. Дирак 1982.
49. Джейнс 2003.
50. Эйнштейн 1998, стр. 682.

Общие источники

• «Приложения квантовой механики». Конспект лекций по курсу AP3303 . Кафедра квантовой нанонауки в Техническом университете Делфта. 2022.
• Аронс, АБ; Пеппард, МБ (1965). «Предложение Эйнштейна о концепции фотона: перевод статьи Annalen der Physik 1905 года» (PDF) . American Journal of Physics . 33 (5): 367. Bibcode :1965AmJPh..33..367A. doi :10.1119/1.1971542.
• Аткинс, П. У. (1974). Quanta: Справочник концепций . Clarendon Press. ISBN 978-0-19-855494-3.
• Бор, Н. (1985). Калькар, Дж. (ред.). Нильс Бор - Собрание сочинений: Основы квантовой физики I (1926 - 1932) . Том 6. Амстердам: Северная Голландия. ISBN 978-044453289-3.
• Борн, М. (1926а). «Квантовая механика дер Стосворганге». З. Физ . 37 (12): 863–867. Бибкод : 1926ZPhy...37..863B. дои : 10.1007/bf01397477. S2CID  119896026.
• Борн, М. (1926б). «Квантенмеханик дер Стосворганге». З. Физ . 38 (11–12): 803–827. Бибкод : 1926ZPhy...38..803B. дои : 10.1007/bf01397184. S2CID  126244962.
• Борн, М. (1927). «Физические аспекты квантовой механики». Nature . 119 (2992): 354–357. Bibcode :1927Natur.119..354B. doi : 10.1038/119354a0 .
• Борн, М. (11 декабря 1954 г.). «Статистическая интерпретация квантовой механики». Нобелевская лекция . 122 (3172). Нобелевский фонд : 675–9. doi :10.1126/science.122.3172.675. PMID  17798674.
• де Бройль, Л. (1923). «Радиации — Ondes et quanta» [Радиация — Волны и кванты]. Comptes Rendus (на французском языке). 177 : 507–510, 548, 630.Электронная версия (на французском) Электронная версия (на английском)
• де Бройль, Л. (1960). Нелинейная волновая механика: причинная интерпретация . Амстердам: Elsevier – через Интернет-архив .
• Байрон, Ф. У.; Фуллер, Р. У. (1992) [Впервые опубликовано в 1969]. Математика классической и квантовой физики. Dover Books on Physics (пересмотренное издание). Dover Publications . ISBN 978-0-486-67164-2– через Интернет-архив .
• Камиллери, К. (2009). Гейзенберг и интерпретация квантовой механики: физик как философ . Кембридж, Великобритания: Cambridge University Press. ISBN 978-0-521-88484-6.
• Conway, JB (1990). Курс функционального анализа . Graduate Texts in Mathematics. Vol. 96. Springer Verlag . ISBN 978-0-387-97245-9.
• Дирак, П. А. М. (1939). «Новая нотация для квантовой механики». Математические труды Кембриджского философского общества . 35 (3): 416–418. Bibcode : 1939PCPS...35..416D. doi : 10.1017/S0305004100021162. S2CID  121466183.
• Дирак, П. А. М. (1982). Принципы квантовой механики . Международная серия монографий по физике (4-е изд.). Oxford University Press. ISBN 0-19-852011-5.
• Эйнштейн, А. (1905). «Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt». Аннален дер Физик (на немецком языке). 17 (6): 132–148. Бибкод : 1905АнП...322..132Е. дои : 10.1002/andp.19053220607 .
• Эйнштейн, А. (1916). «Квантовая теория излучения». Mitteilungen der Physikalischen Gesellschaft Zürich . 18 : 47–62.
• Эйнштейн, А. (1917). «Квантовая теория излучения». Physikalische Zeitschrift (на немецком языке). 18 : 121–128. Бибкод : 1917PhyZ...18..121E.
• Эйнштейн, А. (1998). Шилпп, П. А. (ред.). Альберт Эйнштейн: Философ-ученый . Библиотека живых философов. Том VII (3-е изд.). Издательская компания La Salle, Иллинойс: Открытый суд. ISBN 978-0-87548-133-3.
• Айсберг, Роберт Мартин; Резник, Роберт (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). John Wiley & Sons. ISBN 978-0-471-87373-0– через Интернет-архив .
• Грейнер, В.; Рейнхардт, Дж. (2008). Квантовая электродинамика (4-е изд.). Springer. ISBN 978-354087560-4.
• Гриффитс, DJ (2004). Введение в квантовую механику (2-е изд.). Эссекс, Англия: Pearson Education. ISBN 978-013111892-8.
• Гриффитс, Дэвид (2008). Введение в элементарные частицы. Wiley-VCH. С. 162 и далее. ISBN 978-3-527-40601-2.
• тер Хаар, Д. (1967). Старая квантовая теория . Pergamon Press . стр. 167–183. LCCN  66029628 – через Интернет-архив .
• Ханле, П. А. (1977), «Реакция Эрвина Шредингера на тезис Луи де Бройля о квантовой теории», Isis , 68 (4): 606–609, doi :10.1086/351880, S2CID  121913205
• Гейзенберг, В. (1958). Физика и философия: революция в современной науке . Нью-Йорк: Harper & Row – через Интернет-архив .
• Jaynes, ET (2003). Larry, G. (ред.). Теория вероятностей: логика науки . Cambridge University Press . ISBN 978-0-521 59271-0.
• Ландау, Л. Д.; Лифшиц , Э. М. (1977). Квантовая механика: нерелятивистская теория . Т. 3 (3-е изд.). Pergamon Press . ISBN 978-0-08-020940-1.Электронная копия
• Ландсман, Н. П. (2009). «Правило Борна и его интерпретация» (PDF) . Компендиум по квантовой физике . Берлин, Гейдельберг: Springer Berlin Heidelberg. стр. 64–70. doi :10.1007/978-3-540-70626-7_20. ISBN 978-3-540-70622-9.
• Лернер, Р. Г .; Тригг, Г. Л. (1991). Энциклопедия физики (2-е изд.). VHC Publishers. ISBN 978-0-89573-752-6– через Интернет-архив .
• Людвиг, Г. (1968). Волновая механика . Оксфорд, Великобритания: Pergamon Press. ISBN 978-0-08-203204-5. LCCN  66-30631 – через Интернет-архив .
• Мартин, BR; Шоу, G. (2008). Физика частиц . Серия Manchester Physics (3-е изд.). John Wiley & Sons. ISBN 978-0-470-03294-7.
• Мердок, Д. (1987). Философия физики Нильса Бора . Кембридж, Великобритания: Cambridge University Press. ISBN 978-0-521-33320-7– через Интернет-архив .
• Ньютон, РГ (2002). Квантовая физика: учебник для аспирантов . Нью-Йорк: Springer. ISBN 978-0-387-95473-8.
• Паули, Вольфганг (1927). «Квантовая механика магнитных электронов». Zeitschrift für Physik (на немецком языке). 43 (9–10): 601–623. Бибкод : 1927ZPhy...43..601P. дои : 10.1007/bf01397326. S2CID  128228729.
• Пелег, Ю.; Пнини, Р.; Заарур, Э.; Хехт, Э. (2010). Квантовая механика . Очерки Шаума (2-е изд.). МакГроу Хилл. ISBN 978-0-07-162358-2.
• Rae, AIM (2008). Квантовая механика. Том 2 (5-е изд.). Taylor & Francis Group. ISBN 978-1-5848-89700.
• Шредингер, Э. (1926). "Волновая теория механики атомов и молекул" (PDF) . Physical Review . 28 (6): 1049–1070. Bibcode :1926PhRv...28.1049S. doi :10.1103/PhysRev.28.1049. Архивировано из оригинала (PDF) 17 декабря 2008 г.
• Шанкар, Р. (1994). Принципы квантовой механики (2-е изд.). ISBN 978-030644790-7.
• Типлер, П.А.; Моска, Г.; Фримен (2008). Физика для ученых и инженеров – с современной физикой (6-е изд.). WH Freeman. ISBN 978-0-7167-8964-2.
• Тревес, Франсуа (2006). Топологические векторные пространства, распределения и ядра . Минеола, Нью-Йорк: Courier Corporation. ISBN 978-0-486-45352-1.
• Вайнберг, С. (2002), Квантовая теория полей, т. 1, Cambridge University Press, ISBN 978-0-521-55001-7– через Интернет-архив
• Вайнберг, С. (2013), Лекции по квантовой механике , Cambridge University Press, ISBN 978-1-107-02872-2
• Уилер, JA ; Зурек, WH (1983). Квантовая теория и измерения . Принстон, Нью-Джерси: Издательство Принстонского университета.
• Young, HD; Freedman, RA (2008). Pearson (ред.). Университетская физика Сирса и Земанского (12-е изд.). Addison-Wesley. ISBN 978-0-321-50130-1.
• Zettili, N. (2009). Квантовая механика: концепции и приложения (2-е изд.). Wiley. ISBN 978-0-470-02679-3.
• Цвибах, Бартон (2009). Первый курс теории струн . Cambridge University Press. ISBN 978-0-521-88032-9.

Дальнейшее чтение

• Ким, Ён-Ки (2 сентября 2000 г.). Практическая атомная физика (PDF) . Национальный институт стандартов и технологий. стр. 1 (55 с). Архивировано из оригинала (PDF) 22 июля 2011 г.
• Полкингхорн, Джон (2002). Квантовая теория, очень краткое введение . Oxford University Press. ISBN 978-0-19-280252-1.

Внешние ссылки

• Квантовая механика для инженеров
• Спиновые волновые функции Нью-Йоркского университета
• Возвращаясь к идентичным частицам, Майкл Фаулер
• Природа многоэлектронных волновых функций
• Квантовая механика и квантовые вычисления в BerkeleyX Архивировано 13.05.2013 на Wayback Machine
• Эйнштейн, Квантовая теория излучения