Гильбертово пространство

Тип топологического векторного пространства

Состояние колеблющейся струны можно смоделировать как точку в гильбертовом пространстве. Разложение колеблющейся струны на ее колебания по отдельным обертонам задается проекцией точки на оси координат в пространстве.

В математике гильбертовы пространства (названные в честь Дэвида Гильберта ) позволяют обобщать методы линейной алгебры и исчисления от (конечномерных) евклидовых векторных пространств до пространств , которые могут быть бесконечномерными . Гильбертовы пространства естественным образом и часто возникают в математике и физике , обычно как функциональные пространства . Формально гильбертово пространство — это векторное пространство, снабженное скалярным произведением , которое индуцирует функцию расстояния , для которой пространство является полным метрическим пространством .

Самые ранние гильбертовы пространства изучались с этой точки зрения в первом десятилетии 20-го века Давидом Гильбертом , Эрхардом Шмидтом и Фриджесом Риссом . Они являются незаменимыми инструментами в теориях уравнений в частных производных , квантовой механике , анализе Фурье (который включает приложения к обработке сигналов и теплопередаче) и эргодической теории (которая формирует математическую основу термодинамики ). Джон фон Нейман ввел термин «гильбертово пространство» для обозначения абстрактной концепции, лежащей в основе многих из этих разнообразных приложений. Успех методов гильбертова пространства открыл очень плодотворную эпоху функционального анализа . Помимо классических евклидовых векторных пространств, примеры гильбертовых пространств включают пространства интегрируемых с квадратом функций , пространства последовательностей , пространства Соболева, состоящие из обобщенных функций , и пространства Харди голоморфных функций .

Геометрическая интуиция играет важную роль во многих аспектах теории гильбертова пространства. Точные аналоги теоремы Пифагора и закона параллелограмма справедливы в гильбертовом пространстве. На более глубоком уровне перпендикулярная проекция на линейное подпространство или подпространство (аналог « понижения высоты » треугольника ) играет значительную роль в задачах оптимизации и других аспектах теории. Элемент гильбертова пространства может быть однозначно задан своими координатами относительно ортонормированного базиса по аналогии с декартовыми координатами в классической геометрии. Когда этот базис счетно бесконечен , он позволяет отождествить гильбертово пространство с пространством бесконечных последовательностей , суммируемых с квадратом . Последнее пространство в старой литературе часто называют гильбертовым пространством.

Определение и иллюстрация

Мотивирующий пример: евклидово векторное пространство.

Одним из наиболее известных примеров гильбертова пространства является евклидово векторное пространство, состоящее из трехмерных векторов , обозначаемое R ³ и снабженное скалярным произведением . Скалярное произведение принимает два вектора x и y и дает действительное число x ⋅ y . Если x и y представлены в декартовых координатах , то скалярное произведение определяется выражением

$${\displaystyle {\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\cdot {\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\end{pmatrix}}=x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}\,.}$$

Скалярное произведение удовлетворяет свойствам ^[1]

1. Он симметричен по x и y : x ⋅ y знак равно y ⋅ x .
2. Он линеен по своему первому аргументу: ( a x ₁ + b x ₂ ) ⋅ y = a ( x ₁ ⋅ y ) + b ( x ₂ ⋅ y ) для любых скаляров a , b и векторов x ₁ , x ₂ , и й .
3. Оно положительно определено : для всех векторов x , x ⋅ x ≥ 0 , с равенством тогда и только тогда, когда x = 0 .

Операция над парами векторов, которая, как и скалярное произведение, удовлетворяет этим трем свойствам, называется (реальным) внутренним произведением . Векторное пространство , оснащенное таким внутренним продуктом, известно как (реальное) пространство внутреннего продукта . Каждое конечномерное пространство внутреннего произведения также является гильбертовым пространством. ^[2] Основная особенность скалярного произведения, которое связывает его с евклидовой геометрией, заключается в том, что оно связано как с длиной (или нормой ) вектора, обозначаемого ‖ x ‖ , так и с углом θ между двумя векторами x и y соотношением средства формулы

$${\displaystyle \mathbf {x} \cdot \mathbf {y} =\left\|\mathbf {x} \right\|\left\|\mathbf {y} \right\|\,\cos \theta \,.}$$

Полнота означает, что если частица движется по ломаному пути (синий цвет), преодолевая конечное общее расстояние, то частица имеет четко определенное суммарное смещение (оранжевый цвет).

Многомерное исчисление в евклидовом пространстве основано на способности вычислять пределы и иметь полезные критерии для вывода о существовании пределов. Математический ряд

$${\displaystyle \sum _{n=0}^{\infty }\mathbf {x} _{n}}$$

R3 ^, абсолютно сходится^[3]

$${\displaystyle \sum _{k=0}^{\infty }\|\mathbf {x} _{k}\|<\infty \,.}$$

Как и в случае с рядом скаляров, абсолютно сходящаяся серия векторов также сходится к некоторому предельному вектору L в евклидовом пространстве в том смысле, что

$${\displaystyle {\Biggl \|}\mathbf {L} -\sum _{k=0}^{N}\mathbf {x} _{k}{\Biggr \|}\to 0\quad {\text{as }}N\to \infty \,.}$$

Это свойство выражает полноту евклидова пространства: ряд, который сходится абсолютно, сходится и в обычном смысле.

В гильбертовых пространствах часто используются комплексные числа . Комплексная плоскость , обозначенная C, наделена понятием величины, комплексного модуля | г | , который определяется как квадратный корень произведения z на его комплексно-сопряженное число :

$${\displaystyle |z|^{2}=z{\overline {z}}\,.}$$

Если z = x + iy — разложение z на действительную и мнимую части, то модуль — это обычная евклидова двумерная длина:

$${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}\,.}$$

Внутренний продукт пары комплексных чисел z и w — это произведение z на комплексно-сопряженное число w :

$${\displaystyle \langle z,w\rangle =z{\overline {w}}\,.}$$

Это комплексное значение. Действительная часть ⟨ z , w ⟩ дает обычное двумерное евклидово скалярное произведение .

_{Вторым примером} является пространство C2 ^, _{элементами} которого являются пары комплексных чисел z = ( z1 , z2 ) . Тогда скалярное произведение z с другим таким вектором w = ( w ₁ , w ₂ ) определяется выражением

$${\displaystyle \langle z,w\rangle =z_{1}{\overline {w_{1}}}+z_{2}{\overline {w_{2}}}\,.}$$

Действительная часть ⟨ z , w ⟩ тогда является двумерным евклидовым скалярным произведением. Этот внутренний продукт является эрмитовым симметричным, что означает, что результатом замены z и w является комплексно-сопряженное выражение:

$${\displaystyle \langle w,z\rangle ={\overline {\langle z,w\rangle }}\,.}$$

Определение

Гильбертово пространство — это вещественное или комплексное пространство внутреннего произведения , которое также является полным метрическим пространством относительно функции расстояния, индуцированной внутренним произведением. ^[4]

Сказать, что комплексное векторное пространство H является пространством комплексного внутреннего продукта, означает, что существует внутренний продукт , связывающий комплексное число с каждой парой элементов H , который удовлетворяет следующим свойствам: ${\displaystyle \langle x,y\rangle }$ ${\displaystyle x,y}$

1. Внутренний продукт сопряжен симметричен; то есть внутренний продукт пары элементов равен комплексно-сопряженному внутреннему продукту замененных элементов:
   $${\displaystyle \langle y,x\rangle ={\overline {\langle x,y\rangle }}\,.}$$
   Важно отметить, что это означает, что это действительное число. ${\displaystyle \langle x,x\rangle }$
2. Внутренний продукт линеен по своему первому аргументу ^{[nb 1]} . Для всех комплексных чисел и ${\displaystyle a}$ ${\displaystyle b,}$
   $${\displaystyle \langle ax_{1}+bx_{2},y\rangle =a\langle x_{1},y\rangle +b\langle x_{2},y\rangle \,.}$$
3. Внутренний продукт элемента сам на себя положительно определен :
   $${\displaystyle {\begin{alignedat}{4}\langle x,x\rangle >0&\quad {\text{ if }}x\neq 0,\\\langle x,x\rangle =0&\quad {\text{ if }}x=0\,.\end{alignedat}}}$$

Из свойств 1 и 2 следует, что комплексное скалярное произведение является антилинейным , также называемым сопряженным линейным , по второму аргументу, что означает, что

$${\displaystyle \langle x,ay_{1}+by_{2}\rangle ={\bar {a}}\langle x,y_{1}\rangle +{\bar {b}}\langle x,y_{2}\rangle \,.}$$

Реальное пространство внутреннего продукта определяется таким же образом, за исключением того, что H является реальным векторным пространством, а внутренний продукт принимает действительные значения. Такой внутренний продукт будет билинейной картой и образует двойственную систему . ^[5] ${\displaystyle (H,H,\langle \cdot ,\cdot \rangle )}$

Норма – это вещественная функция

$${\displaystyle \|x\|={\sqrt {\langle x,x\rangle }}\,,}$$

H ${\displaystyle d}$ ${\displaystyle x,y}$

$${\displaystyle d(x,y)=\|x-y\|={\sqrt {\langle x-y,x-y\rangle }}\,.}$$

То, что эта функция является функцией расстояния, означает, во-первых, что она симметрична , во-вторых, что расстояние между и само по себе равно нулю, в противном случае расстояние между и должно быть положительным, и, наконец, что выполняется неравенство треугольника , означающее, что длина одного катета треугольника xyz не может превышать сумму длин двух других катетов: ${\displaystyle x}$ ${\displaystyle y,}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$

$${\displaystyle d(x,z)\leq d(x,y)+d(y,z)\,.}$$

Это последнее свойство в конечном итоге является следствием более фундаментального неравенства Коши – Шварца , которое утверждает

$${\displaystyle \left|\langle x,y\rangle \right|\leq \|x\|\|y\|}$$

линейно ${\displaystyle x}$ ${\displaystyle y}$

С функцией расстояния, определенной таким образом, любое пространство внутреннего произведения является метрическим пространством и иногда называется хаусдорфовым предгильбертовым пространством . ^[6] Любое прегильбертово пространство, которое к тому же является полным пространством, является гильбертовым пространством. ^[7]

Полнота H выражается с использованием формы критерия Коши для последовательностей в H : прегильбертово пространство H является полным, если каждая последовательность Коши сходится относительно этой нормы к элементу в пространстве. Полноту можно охарактеризовать следующим эквивалентным условием: если ряд векторов

$${\displaystyle \sum _{k=0}^{\infty }u_{k}}$$

абсолютно сходится

$${\displaystyle \sum _{k=0}^{\infty }\|u_{k}\|<\infty \,,}$$

Hчастичные суммыH^[8]

Как полное нормированное пространство, гильбертово пространство по определению также является банаховым пространством . По сути, они являются топологическими векторными пространствами , в которых четко определены топологические понятия, такие как открытость и замкнутость подмножеств . Особое значение имеет понятие замкнутого линейного подпространства гильбертова пространства, которое со скалярным произведением, индуцированным ограничением , также является полным (будучи замкнутым множеством в полном метрическом пространстве) и, следовательно, само по себе является гильбертовым пространством.

Второй пример: пространства последовательностей

Пространство последовательностей l ² состоит из всех бесконечных последовательностей z = ( z ₁ , z ₂ , …) комплексных чисел таких, что сходится следующий ряд : ^[9]

$${\displaystyle \sum _{n=1}^{\infty }|z_{n}|^{2}}$$

Внутренний продукт на l ² определяется следующим образом:

$${\displaystyle \langle \mathbf {z} ,\mathbf {w} \rangle =\sum _{n=1}^{\infty }z_{n}{\overline {w_{n}}}\,,}$$

Этот второй ряд сходится вследствие неравенства Коши – Шварца и сходимости предыдущего ряда.

Полнота пространства имеет место при условии, что всякий раз, когда ряд элементов из l ² сходится абсолютно (по норме), то он сходится к элементу из l ² . Доказательство является базовым в математическом анализе и позволяет манипулировать математическими рядами элементов пространства с той же легкостью, что и рядами комплексных чисел (или векторами в конечномерном евклидовом пространстве). ^[10]

История

Дэвид Хилберт

До разработки гильбертовых пространств математикам и физикам были известны и другие обобщения евклидовых пространств . В частности, идея абстрактного линейного пространства (векторного пространства) получила некоторую популярность к концу XIX века: ^[11] это пространство, элементы которого можно складывать и умножать на скаляры (например, действительные или комплексные числа) . ) без обязательного отождествления этих элементов с «геометрическими» векторами , такими как векторы положения и импульса в физических системах. Другие объекты, изучаемые математиками на рубеже 20-го века, в частности пространства последовательностей (в том числе рядов ) и пространства функций, ^[12] естественно можно рассматривать как линейные пространства. Функции, например, можно складывать или умножать на постоянные скаляры, и эти операции подчиняются алгебраическим законам, которым удовлетворяют сложение и скалярное умножение пространственных векторов.

В первом десятилетии 20-го века параллельные разработки привели к введению гильбертовых пространств. Первым из них было наблюдение, возникшее во время исследования Дэвидом Гильбертом и Эрхардом Шмидтом интегральных уравнений ^[13] , что две интегрируемые с квадратом вещественные функции f и g на интервале [ a , b ] имеют скалярное произведение

${\displaystyle \langle f,g\rangle =\int _{a}^{b}f(x)g(x)\,\mathrm {d} x}$

которое обладает многими знакомыми свойствами евклидова скалярного произведения. В частности, имеет смысл идея ортогонального семейства функций. Шмидт использовал сходство этого скалярного произведения с обычным скалярным произведением, чтобы доказать аналог спектрального разложения для оператора вида

${\displaystyle f(x)\mapsto \int _{a}^{b}K(x,y)f(y)\,\mathrm {d} y}$

где K — непрерывная функция, симметричная по x и y . Полученное разложение по собственным функциям выражает функцию K в виде ряда вида

${\displaystyle K(x,y)=\sum _{n}\lambda _{n}\varphi _{n}(x)\varphi _{n}(y)}$

где функции φ _n ортогональны в том смысле, что ⟨ φ _n , φ _m ⟩ = 0 для всех n ≠ m . Отдельные термины в этой серии иногда называют элементарными решениями продукта. Однако существуют разложения по собственным функциям, которые не могут сходиться в подходящем смысле к функции, интегрируемой с квадратом: недостающим ингредиентом, обеспечивающим сходимость, является полнота. ^[14]

Вторым развитием стал интеграл Лебега , альтернатива интегралу Римана , введенному Анри Лебегом в 1904 году. ^[15] Интеграл Лебега позволил интегрировать гораздо более широкий класс функций. В 1907 году Фридьес Рисс и Эрнст Сигизмунд Фишер независимо доказали ^, что пространство L2 функций, интегрируемых с квадратом по Лебегу, является полным метрическим пространством . ^[16] В результате взаимодействия между геометрией и полнотой результаты XIX века Жозефа Фурье , Фридриха Бесселя и Марка-Антуана Парсеваля о тригонометрических рядах легко переносятся на эти более общие пространства, в результате чего теперь обычно образуется геометрический и аналитический аппарат. известная как теорема Рисса-Фишера . ^[17]

Дальнейшие основные результаты были доказаны в начале 20 века. Например, теорема о представлении Рисса была независимо установлена ​​Морисом Фреше и Фриджесом Риссом в 1907 году. ^[18] Джон фон Нейман ввёл термин « абстрактное гильбертово пространство» в своей работе о неограниченных эрмитовых операторах . ^[19] Хотя другие математики, такие как Герман Вейль и Норберт Винер, уже очень подробно изучали отдельные гильбертовы пространства, часто с физически мотивированной точки зрения, фон Нейман дал первое полное и аксиоматическое их рассмотрение. ^[20] Фон Нейман позже использовал их в своей основополагающей работе по основам квантовой механики, ^[21] и в своей дальнейшей работе с Юджином Вигнером . Название «гильбертово пространство» вскоре было принято другими, например, Германом Вейлем в его книге по квантовой механике и теории групп. ^[22]

Значимость концепции гильбертова пространства была подчеркнута осознанием того, что она предлагает одну из лучших математических формулировок квантовой механики . ^[23] Короче говоря, состояния квантово-механической системы являются векторами в определенном гильбертовом пространстве, наблюдаемые — эрмитовыми операторами в этом пространстве, симметрии системы — унитарными операторами , а измерения — ортогональными проекциями . Связь между квантово-механическими симметриями и унитарными операторами дала толчок развитию теории унитарного представления групп , начатой ​​в 1928 году работой Германа Вейля. ^[22] С другой стороны, в начале 1930-х годов стало ясно, что классическую механику можно описать в терминах гильбертова пространства ( классическая механика Купмана – фон Неймана ) и что некоторые свойства классических динамических систем можно анализировать с использованием методов гильбертова пространства в в рамках эргодической теории . ^[24]

Алгебра наблюдаемых в квантовой механике, естественно, является алгеброй операторов, определенных в гильбертовом пространстве, согласно матричной формулировке квантовой теории Вернера Гейзенберга . ^[25] Фон Нейман начал исследовать операторные алгебры в 1930-х годах как кольца операторов в гильбертовом пространстве. Вид алгебр, изучаемых фон Нейманом и его современниками, теперь известен как алгебры фон Неймана . ^[26] В 1940-х годах Исраэль Гельфанд , Марк Наймарк и Ирвинг Сигал дали определение своего рода операторных алгебр, называемых C*-алгебрами , которые, с одной стороны, не делали ссылок на лежащее в основе гильбертово пространство, а с другой экстраполировали многие из полезные особенности ранее изученных операторных алгебр. Спектральная теорема для самосопряженных операторов, лежащая в основе большей части существующей теории гильбертового пространства, была обобщена на С*-алгебры. ^[27] Эти методы сейчас являются базовыми в абстрактном гармоническом анализе и теории представлений.

Примеры

Пространства Лебега

Пространства Лебега — это функциональные пространства , связанные с пространствами с мерой ( X , M , µ ) , где X — множество, M — σ-алгебра подмножеств X , а µ — счётно-аддитивная мера на M. Пусть L ² ( X , µ ) — пространство тех комплекснозначных измеримых функций на X , для которых интеграл Лебега от квадрата модуля функции конечен, т. е. для функции f из L ² ( X , мкм ) ,

$${\displaystyle \int _{X}|f|^{2}\mathrm {d} \mu <\infty \,,}$$

множестве нулевой меры

Тогда скалярное произведение функций f и g в L ² ( X , µ ) определяется как

$${\displaystyle \langle f,g\rangle =\int _{X}f(t){\overline {g(t)}}\,\mathrm {d} \mu (t)}$$

$${\displaystyle \langle f,g\rangle =\int _{X}{\overline {f(t)}}g(t)\,\mathrm {d} \mu (t)\,,}$$

где вторая форма (сопряжение первого элемента) обычно встречается в литературе по теоретической физике . Для f и g в L ² интеграл существует благодаря неравенству Коши–Шварца и определяет скалярное произведение в пространстве. Оснащенный этим внутренним продуктом, L ² фактически является завершенным. ^[28] Интеграл Лебега необходим для обеспечения полноты: например, в областях действительных чисел недостаточно функций, интегрируемых по Риману . ^[29]

Пространства Лебега встречаются во многих природных условиях. Пространства L ² ( R ) и L ² ([0,1]) функций, интегрируемых с квадратом относительно меры Лебега на действительной прямой и единичном интервале соответственно, являются естественными областями, на которых можно определить преобразование Фурье и Фурье. ряд. В других ситуациях мера может быть чем-то иным, чем обычная мера Лебега на действительной прямой. Например, если w — любая положительная измеримая функция, пространство всех измеримых функций f на интервале [0, 1] , удовлетворяющих

$${\displaystyle \int _{0}^{1}{\bigl |}f(t){\bigr |}^{2}w(t)\,\mathrm {d} t<\infty }$$

весовым L2 ^- пространством L²
_Вт([0, 1])w

$${\displaystyle \langle f,g\rangle =\int _{0}^{1}f(t){\overline {g(t)}}w(t)\,\mathrm {d} t\,.}$$

Весовое пространство L²
_Вт([0, 1]) тождественно гильбертовому пространству L ² ([0, 1], µ ) , где мера µ измеримого по Лебегу множества A определяется формулой

$${\displaystyle \mu (A)=\int _{A}w(t)\,\mathrm {d} t\,.}$$

Подобные весовые пространства L ² часто используются для изучения ортогональных многочленов , поскольку разные семейства ортогональных многочленов ортогональны относительно разных весовых функций. ^[30]

Соболевские пространства

Пространства Соболева , обозначаемые H ^s или W ^{s , 2} , являются гильбертовыми пространствами. Это особый вид функционального пространства , в котором может выполняться дифференцирование , но которое (в отличие от других банаховых пространств , таких как пространства Гёльдера ) поддерживает структуру внутреннего продукта. Поскольку дифференцирование разрешено, пространства Соболева являются удобным инструментом для теории уравнений в частных производных . ^[31] Они также составляют основу теории прямых методов вариационного исчисления . ^[32]

Если s — неотрицательное целое число и Ω ⊂ Rn ^, пространство Соболева H ^s (Ω) содержит L ² функций, слабые производные которых порядка до s также являются L ² . Скалярный продукт в H ^s (Ω) равен

$${\displaystyle \langle f,g\rangle =\int _{\Omega }f(x){\bar {g}}(x)\,\mathrm {d} x+\int _{\Omega }Df(x)\cdot D{\bar {g}}(x)\,\mathrm {d} x+\cdots +\int _{\Omega }D^{s}f(x)\cdot D^{s}{\bar {g}}(x)\,\mathrm {d} x}$$

s

Пространства Соболева изучаются также с точки зрения спектральной теории, более конкретно опираясь на структуру гильбертова пространства. Если Ω — подходящая область, то пространство Соболева H ^s (Ω) можно определить как пространство потенциалов Бесселя ; ^[33] примерно,

$${\displaystyle H^{s}(\Omega )=\left\{(1-\Delta )^{-s/2}f\mathrel {\Big |} f\in L^{2}(\Omega )\right\}\,.}$$

Здесь ∆ — лапласиан, а (1 — ∆) ^{— s  /2} понимается в терминах теоремы о спектральном отображении . Помимо предоставления работоспособного определения пространств Соболева для нецелых чисел , это определение также обладает особенно желательными свойствами при преобразовании Фурье , которые делают его идеальным для изучения псевдодифференциальных операторов . Используя эти методы на компактном римановом многообразии , можно получить, например, разложение Ходжа , которое является основой теории Ходжа . ^[34]

Пространства голоморфных функций

Выносливые пространства

Пространства Харди — это функциональные пространства, возникающие в комплексном анализе и гармоническом анализе , элементами которого являются некоторые голоморфные функции в комплексной области. ^[35] Пусть U обозначает единичный круг в комплексной плоскости. Тогда пространство Харди H ² ( U ) определяется как пространство голоморфных функций f на U таких, что средние

$${\displaystyle M_{r}(f)={\frac {1}{2\pi }}\int _{0}^{2\pi }\left|f{\bigl (}re^{i\theta }{\bigr )}\right|^{2}\,\mathrm {d} \theta }$$

остаются ограниченными при r < 1 . Норма в этом пространстве Харди определяется формулой

$${\displaystyle \left\|f\right\|_{2}=\lim _{r\to 1}{\sqrt {M_{r}(f)}}\,.}$$

Пространства Харди в диске относятся к рядам Фурье. Функция f находится в H ² ( U ) тогда и только тогда, когда

$${\displaystyle f(z)=\sum _{n=0}^{\infty }a_{n}z^{n}}$$

$${\displaystyle \sum _{n=0}^{\infty }|a_{n}|^{2}<\infty \,.}$$

Таким образом, H ² ( U ) состоит из тех функций, которые являются L ² на окружности и у которых отрицательные частотные коэффициенты Фурье равны нулю.

Пространства Бергмана

Пространства Бергмана — это еще одно семейство гильбертовых пространств голоморфных функций. ^[36] Пусть D — ограниченное открытое множество в комплексной плоскости (или многомерное комплексное пространство) и пусть L2 ^{, h} ( D ) — пространство голоморфных функций f в D , ^{которые} также находятся в L2 ( D ). в смысле

$${\displaystyle \|f\|^{2}=\int _{D}|f(z)|^{2}\,\mathrm {d} \mu (z)<\infty \,,}$$

где интеграл берется по мере Лебега в D . Ясно, что ^L2 , ^{h (} D ) — подпространство L2 ( D ) ; на самом деле это замкнутое подпространство и, следовательно, само по себе гильбертово пространство. Это является следствием оценки, справедливой на компактных подмножествах K в D , что

$${\displaystyle \sup _{z\in K}\left|f(z)\right|\leq C_{K}\left\|f\right\|_{2}\,,}$$

интегральной формулы КошиL2 ( D )компактная сходимость ^,fDL ^{2, h} ( D )L ^{2, h} ( D )z ∈ Dη _z ∈ L ^{2, h} ( D )

$${\displaystyle f(z)=\int _{D}f(\zeta ){\overline {\eta _{z}(\zeta )}}\,\mathrm {d} \mu (\zeta )}$$

f ∈ L ^{2, час} ( D )

$${\displaystyle K(\zeta ,z)={\overline {\eta _{z}(\zeta )}}}$$

ядро ​​Бергманаинтегральное ядро

$${\displaystyle f(z)=\int _{D}f(\zeta )K(\zeta ,z)\,\mathrm {d} \mu (\zeta )\,.}$$

Пространство Бергмана является примером воспроизводящего ядра гильбертова пространства , которое представляет собой гильбертово пространство функций вместе с ядром K ( ζ , z ) , которое проверяет воспроизводящее свойство, аналогичное этому. Пространство Харди H2 ⁽ D ) также допускает воспроизводящее ядро, известное как ядро ​​Сегё . ^[37] Воспроизводящие ядра распространены и в других областях математики. Например, в гармоническом анализе ядро ​​Пуассона является воспроизводящим ядром для гильбертова пространства интегрируемых с квадратом гармонических функций в единичном шаре . То, что последнее вообще является гильбертовым пространством, является следствием теоремы о среднем значении для гармонических функций.

Приложения

Во многих приложениях гильбертовых пространств используется тот факт, что гильбертовы пространства поддерживают обобщения простых геометрических концепций, таких как проекция и замена базиса, из их обычной конечномерной ситуации. В частности, спектральная теория непрерывных самосопряженных линейных операторов в гильбертовом пространстве обобщает обычное спектральное разложение матрицы , и это часто играет важную роль в приложениях теории к другим областям математики и физики.

Теория Штурма – Лиувилля

Обертоны вибрирующей струны . Это собственные функции ассоциированной задачи Штурма – Лиувилля. Собственные значения 1,1/2,1/3, ... образуют (музыкальный) гармонический ряд .

В теории обыкновенных дифференциальных уравнений для изучения поведения собственных значений и собственных функций дифференциальных уравнений применяются спектральные методы на подходящем гильбертовом пространстве. Например, задача Штурма–Лиувилля возникает при исследовании гармоник волн в скрипичной струне или барабане и является центральной проблемой в обыкновенных дифференциальных уравнениях . ^[38] Задача представляет собой дифференциальное уравнение вида

$${\displaystyle -{\frac {\mathrm {d} }{\mathrm {d} x}}\left[p(x){\frac {\mathrm {d} y}{\mathrm {d} x}}\right]+q(x)y=\lambda w(x)y}$$

y[ a , b ]граничным условиям Робина

$${\displaystyle {\begin{cases}\alpha y(a)+\alpha 'y'(a)&=0\\\beta y(b)+\beta 'y'(b)&=0\,.\end{cases}}}$$

pqwyλλкомпактных операторовинтегральному операторуфункцией Гринаλ^{[39] [номер 2]}

Уравнения в частных производных

Гильбертовые пространства представляют собой основной инструмент при изучении уравнений в частных производных . ^[31] Для многих классов уравнений в частных производных, таких как линейные эллиптические уравнения , можно рассмотреть обобщенное решение (известное как слабое решение) путем расширения класса функций. Многие слабые формулировки включают класс функций Соболева , который является гильбертовым пространством. Подходящая слабая формулировка сводится к геометрической задаче, аналитической задаче нахождения решения или, что часто, что более важно, доказывания того, что решение существует и является единственным для заданных граничных данных. Для линейных эллиптических уравнений одним геометрическим результатом, обеспечивающим однозначную разрешимость большого класса задач, является теорема Лакса – Милгрэма . Эта стратегия составляет основу метода Галеркина ( метода конечных элементов ) для численного решения уравнений в частных производных. ^[40]

Типичным примером является уравнение Пуассона −Δ u = g с граничными условиями Дирихле в ограниченной области Ω в R ² . Слабая формулировка состоит в нахождении функции u такой, что для всех непрерывно дифференцируемых функций v в Ω , исчезающих на границе:

$${\displaystyle \int _{\Omega }\nabla u\cdot \nabla v=\int _{\Omega }gv\,.}$$

Это можно переписать в терминах гильбертова пространства H¹
₀(Ω), состоящая из функций u таких, что u вместе со своими слабыми частными производными интегрируемы с квадратом на Ω и обращаются в нуль на границе. Тогда вопрос сводится к нахождению u в этом пространстве такого, что для всех v в этом пространстве

$${\displaystyle a(u,v)=b(v)}$$

где a — непрерывная билинейная форма , а b — непрерывный линейный функционал , определяемый соответственно формулой

$${\displaystyle a(u,v)=\int _{\Omega }\nabla u\cdot \nabla v,\quad b(v)=\int _{\Omega }gv\,.}$$

Поскольку уравнение Пуассона эллиптическое , из неравенства Пуанкаре следует, что билинейная форма a является коэрцитивной . Тогда теорема Лакса – Милгрэма обеспечивает существование и единственность решений этого уравнения. ^[41]

Гильбертовые пространства позволяют формулировать многие эллиптические уравнения в частных производных аналогичным образом, и теорема Лакса – Милгрэма становится тогда основным инструментом в их анализе. С соответствующими модификациями аналогичные методы можно применять к параболическим уравнениям в частных производных и некоторым гиперболическим уравнениям в частных производных . ^[42]

Эргодическая теория

Путь бильярдного шара на стадионе Бунимовича описывается эргодической динамической системой .

Область эргодической теории — изучение долговременного поведения хаотических динамических систем . Типичным случаем поля, к которому применяется эргодическая теория, является термодинамика , в которой — хотя микроскопическое состояние системы чрезвычайно сложно (невозможно понять ансамбль отдельных столкновений между частицами материи) — среднее поведение в течение достаточно длительного времени временные интервалы являются управляемыми. Законы термодинамики являются утверждениями о таком среднем поведении. В частности, одна из формулировок нулевого закона термодинамики утверждает, что в течение достаточно длительного периода времени единственным функционально независимым измерением термодинамической системы, находящейся в равновесии, является ее полная энергия в форме температуры . ^[43]

Эргодическая динамическая система — это такая система, для которой, кроме энергии, измеряемой гамильтонианом , в фазовом пространстве нет других функционально независимых сохраняющихся величин . Более подробно предположим, что энергия E фиксирована, и пусть Ω _E — подмножество фазового пространства, состоящее из всех состояний энергии E (энергетическая поверхность), и пусть T _t обозначает оператор эволюции в фазовом пространстве. Динамическая система является эргодической, если каждая инвариантная измеримая функция на Ω _E постоянна почти всюду . ^[44] Инвариантной функцией f называется такая, для которой

$${\displaystyle f(T_{t}w)=f(w)}$$

wΩ _EtИз теоремы Лиувиллямера µперемещения времениунитарное преобразованиеL ² (Ω _E , µ )Ω _E

$${\displaystyle \left\langle f,g\right\rangle _{L^{2}\left(\Omega _{E},\mu \right)}=\int _{E}f{\bar {g}}\,\mathrm {d} \mu \,.}$$

Эргодическая теорема фон Неймана о среднем ^[24] утверждает следующее:

• Если U _t — (сильно непрерывная) однопараметрическая полугруппа унитарных операторов в гильбертовом пространстве H , а P — ортогональный проектор на пространство общих неподвижных точек U _t , { x ∈ H | U _t x = x , ∀ t > 0} , тогда
  $${\displaystyle Px=\lim _{T\to \infty }{\frac {1}{T}}\int _{0}^{T}U_{t}x\,\mathrm {d} t\,.}$$

Для эргодической системы фиксированное множество временной эволюции состоит только из постоянных функций, поэтому из эргодической теоремы следует следующее: ^[45] для любой функции f ∈ L ² (Ω _E , µ ) ,

$${\displaystyle {\underset {T\to \infty }{L^{2}-\lim }}{\frac {1}{T}}\int _{0}^{T}f(T_{t}w)\,\mathrm {d} t=\int _{\Omega _{E}}f(y)\,\mathrm {d} \mu (y)\,.}$$

То есть среднее значение наблюдаемой f за долгое время равно ее математическому ожиданию по энергетической поверхности.

Фурье-анализ

Суперпозиция базисных функций синусоидальной волны (внизу) для формирования пилообразной волны (вверху)

Сферические гармоники , ортонормированный базис гильбертова пространства функций, интегрируемых с квадратом на сфере, показаны на графике в радиальном направлении.

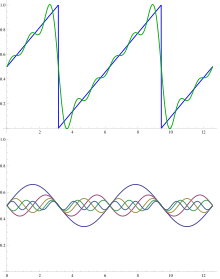
Одной из основных целей анализа Фурье является разложение функции на (возможно, бесконечную) линейную комбинацию заданных базисных функций: соответствующий ряд Фурье . Классический ряд Фурье, связанный с функцией f , определенной на интервале [0, 1], представляет собой ряд вида

$${\displaystyle \sum _{n=-\infty }^{\infty }a_{n}e^{2\pi in\theta }}$$

$${\displaystyle a_{n}=\int _{0}^{1}f(\theta )\;\!e^{-2\pi in\theta }\,\mathrm {d} \theta \,.}$$

Пример сложения первых нескольких членов ряда Фурье для пилообразной функции показан на рисунке. Базисными функциями являются синусоидальные волны с длинами волнλ/н(для целого числа n ) короче длины волны λ самой пилообразной волны (за исключением n = 1 , основной волны). Все базисные функции имеют узлы в узлах пилообразной формы, но все, кроме фундаментальной, имеют дополнительные узлы. Колебание суммированных членов вокруг пилообразного состояния называется феноменом Гиббса .

Важная проблема в классических рядах Фурье заключается в том, в каком смысле ряд Фурье сходится, если вообще сходится, к функции f . Методы гильбертового пространства дают один из возможных ответов на этот вопрос. ^[46] Функции en ( _θ ) = e ^{2π в θ} образуют ортогональный базис гильбертова пространства L 2 ([0, 1 ^] ) . Следовательно, любую интегрируемую с квадратом функцию можно выразить в виде ряда

$${\displaystyle f(\theta )=\sum _{n}a_{n}e_{n}(\theta )\,,\quad a_{n}=\langle f,e_{n}\rangle }$$

и, кроме того, этот ряд сходится в смысле гильбертова пространства (т. е. в среднем L 2 ).

Проблему можно изучать и с абстрактной точки зрения: каждое гильбертово пространство имеет ортонормированный базис , и каждый элемент гильбертова пространства может быть записан уникальным образом как сумма кратных этих базисных элементов. Коэффициенты, возникающие на этих базисных элементах, иногда абстрактно называют коэффициентами Фурье элемента пространства. ^[47] Эта абстракция особенно полезна, когда более естественно использовать разные базисные функции для такого пространства, как L ² ([0, 1]) . Во многих случаях желательно не разлагать функцию на тригонометрические функции, а, например, на ортогональные полиномы или вейвлеты , ^[48] и в более высоких измерениях на сферические гармоники . ^[49]

Например, если en — _любые ортонормированные базисные функции L ² [0, 1] , то данную функцию из L ² [0, 1] можно аппроксимировать как конечную линейную комбинацию ^[50]

$${\displaystyle f(x)\approx f_{n}(x)=a_{1}e_{1}(x)+a_{2}e_{2}(x)+\cdots +a_{n}e_{n}(x)\,.}$$

Коэффициенты { a _j } выбираются так, чтобы величина разности ‖ f − f _n ‖ ² была как можно меньше. Геометрически лучшим приближением является ортогональная проекция f на подпространство, состоящее из всех линейных комбинаций { e _j } , и его можно вычислить по формуле ^[51]

$${\displaystyle a_{j}=\int _{0}^{1}{\overline {e_{j}(x)}}f(x)\,\mathrm {d} x\,.}$$

То, что эта формула минимизирует разность ‖ f − f _n ‖ ² , является следствием неравенства Бесселя и формулы Парсеваля.

В различных приложениях к физическим задачам функция может быть разложена на физически значимые собственные функции дифференциального оператора (обычно оператора Лапласа ): это формирует основу для спектрального исследования функций относительно спектра дифференциального оператора. ^[52] Конкретное физическое приложение включает в себя задачу услышать форму барабана : учитывая основные виды вибрации, которые способен производить пластик, можно ли сделать вывод о форме самого барабана? ^[53] Математическая формулировка этого вопроса включает в себя собственные значения Дирихле уравнения Лапласа на плоскости, которые представляют основные формы вибрации по прямой аналогии с целыми числами, которые представляют основные формы вибрации скрипичной струны.

Спектральная теория также лежит в основе некоторых аспектов преобразования Фурье функции. В то время как анализ Фурье разлагает функцию, определенную на компактном множестве, в дискретный спектр лапласиана (который соответствует колебаниям скрипичной струны или барабана), преобразование Фурье функции представляет собой разложение функции, определенной на всем евклидовом пространстве. на его компоненты в непрерывном спектре лапласиана. Преобразование Фурье также является геометрическим, в некотором смысле уточненным теоремой Планшереля , которая утверждает, что оно представляет собой изометрию одного гильбертова пространства («временная область») с другим («частотная область»). Это свойство изометрии преобразования Фурье является повторяющейся темой в абстрактном гармоническом анализе (поскольку оно отражает сохранение энергии для непрерывного преобразования Фурье), о чем свидетельствует, например, теорема Планшереля для сферических функций , встречающихся в некоммутативном гармоническом анализе .

Квантовая механика

Орбитали электрона в атоме водорода являются собственными функциями энергии . _

В математически строгой формулировке квантовой механики , разработанной Джоном фон Нейманом , ^[54] возможные состояния (точнее, чистые состояния ) квантовомеханической системы представлены единичными векторами (называемыми векторами состояния ), находящимися в комплексном сепарабельном гильбертовом пространстве. пространство, известное как пространство состояний , четко определенное с точностью до комплексного числа нормы 1 (фазового фактора ). Другими словами, возможные состояния — это точки проективизации гильбертова пространства, обычно называемого комплексным проективным пространством . Точная природа этого гильбертова пространства зависит от системы; например, состояния положения и импульса для одиночной нерелятивистской частицы со спином ноль представляют собой пространство всех интегрируемых с квадратом функций, а состояния для спина одного протона являются единичными элементами двумерного комплексного гильбертова пространства спиноров . . Каждая наблюдаемая представляется самосопряженным линейным оператором , действующим в пространстве состояний. Каждое собственное состояние наблюдаемой соответствует собственному вектору оператора, а связанное с ним собственное значение соответствует значению наблюдаемой в этом собственном состоянии. ^[55]

Внутренний продукт между двумя векторами состояния представляет собой комплексное число, известное как амплитуда вероятности . Во время идеального измерения квантово-механической системы вероятность коллапса системы из заданного начального состояния в конкретное собственное состояние определяется квадратом абсолютного значения амплитуд вероятности между начальным и конечным состояниями. ^[56] Возможными результатами измерения являются собственные значения оператора, что объясняет выбор самосопряженных операторов, поскольку все собственные значения должны быть действительными. Распределение вероятностей наблюдаемой в данном состоянии можно найти путем вычисления спектрального разложения соответствующего оператора. ^[57]

Для общей системы состояния обычно не являются чистыми, а вместо этого представляются как статистические смеси чистых состояний или смешанных состояний, заданных матрицами плотности : самосопряженными операторами следа один в гильбертовом пространстве. ^[58] Более того, для общих квантово-механических систем эффекты одного измерения могут влиять на другие части системы таким образом, который вместо этого описывается положительной мерой с операторным значением . Таким образом, структура как состояний, так и наблюдаемых в общей теории значительно сложнее, чем идеализация чистых состояний. ^[59]

Теория вероятности

В теории вероятностей гильбертовы пространства также имеют разнообразные применения. Здесь фундаментальное гильбертово пространство — это пространство случайных величин в заданном вероятностном пространстве , имеющее класс (конечные первый и второй моменты ). Распространенной операцией в статистике является центрирование случайной величины путем вычитания ее математического ожидания . Таким образом, если – случайная величина, то – ее центрирование. С точки зрения гильбертова пространства это ортогональная проекция на ядро ​​оператора ожидания, который является непрерывным линейным функционалом в гильбертовом пространстве (фактически, скалярным произведением с постоянной случайной величиной 1), и поэтому это ядро ​​является замкнутое подпространство. ${\displaystyle L^{2}}$ ${\displaystyle X}$ ${\displaystyle X-E(X)}$ ${\displaystyle X}$

Условное ожидание имеет естественную интерпретацию в гильбертовом пространстве. ^[60] Предположим, что задано вероятностное пространство , где – сигма-алгебра на множестве и – вероятностная мера на пространстве меры . Если – сигма-подалгебра , то условное математическое ожидание – это ортогональная проекция на подпространство, состоящее из -измеримых функций. Если случайная величина в не зависит от сигма-алгебры , то условное математическое ожидание т. е. ее проекция на -измеримые функции постоянна. Эквивалентно, проекция его центрирования равна нулю. ${\displaystyle (\Omega ,P,{\mathcal {B}})}$ ${\displaystyle {\mathcal {B}}}$ ${\displaystyle \Omega }$ ${\displaystyle P}$ ${\displaystyle (\Omega ,{\mathcal {B}})}$ ${\displaystyle {\mathcal {F}}\leq {\mathcal {B}}}$ ${\displaystyle {\mathcal {B}}}$ ${\displaystyle E[X|{\mathcal {F}}]}$ ${\displaystyle X}$ ${\displaystyle L^{2}(\Omega ,P)}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle X}$ ${\displaystyle L^{2}(\Omega ,P)}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle E(X|{\mathcal {F}})=E(X)}$ ${\displaystyle {\mathcal {F}}}$

В частности, если две случайные величины и (в ) независимы, то центрированные случайные величины и ортогональны. (Это означает, что две переменные имеют нулевую ковариацию : они некоррелированы .) В этом случае теорема Пифагора в ядре оператора ожидания подразумевает, что дисперсии и удовлетворяют тождеству: ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle L^{2}(\Omega ,P)}$ ${\displaystyle X-E(X)}$ ${\displaystyle Y-E(Y)}$ ${\displaystyle X}$ ${\displaystyle Y}$

$${\displaystyle \operatorname {Var} (X+Y)=\operatorname {Var} (X)+\operatorname {Var} (Y),}$$

линейной регрессии^[61]дисперсионный анализ

Теорию мартингалов можно сформулировать в гильбертовых пространствах. Мартингал в гильбертовом пространстве — это последовательность элементов гильбертова пространства такая, что для каждого n является ортогональной проекцией на линейную оболочку . ^[62] Если являются случайными величинами, это воспроизводит обычное определение (дискретного) мартингала: ожидание , обусловленное , равно . ${\displaystyle x_{1},x_{2},\dots }$ ${\displaystyle x_{n}}$ ${\displaystyle x_{n+1}}$ ${\displaystyle x_{1},\dots ,x_{n}}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{n+1}}$ ${\displaystyle x_{1},\dots ,x_{n}}$ ${\displaystyle x_{n}}$

Гильбертовы пространства также используются в основах исчисления Ито . ^[63] Любому мартингалу , интегрируемому с квадратом , можно сопоставить гильбертову норму в пространстве классов эквивалентности прогрессивно измеримых процессов относительно мартингала (используя квадратичную вариацию мартингала в качестве меры). Интеграл Ито можно построить, сначала определив его для простых процессов, а затем используя их плотность в гильбертовом пространстве. Примечательным результатом является изометрия Ито , которая подтверждает, что для любого мартингала M , имеющего квадратичную меру вариации , и любого прогрессивно измеримого процесса H : ${\displaystyle d\langle M\rangle _{t}}$

$${\displaystyle E\left[\left(\int _{0}^{t}H_{s}dM_{s}\right)^{2}\right]=E\left[\int _{0}^{t}H_{s}^{2}d\langle M\rangle _{s}\right]}$$

Более глубокое применение гильбертовых пространств, которое особенно важно в теории гауссовских процессов , — это попытка Леонарда Гросса и других понять смысл некоторых формальных интегралов по бесконечномерным пространствам, таких как интеграл по путям Фейнмана из квантовой теории поля . Проблема с подобным интегралом заключается в том, что не существует бесконечномерной меры Лебега . Понятие абстрактного пространства Винера позволяет построить меру на банаховом пространстве B , которое содержит гильбертово пространство H , называемое пространством Кэмерона-Мартина , как плотное подмножество, из конечно-аддитивной меры цилиндрического множества на H. Результирующая мера на B является счетно-аддитивной и инвариантной относительно переноса элементами H , и это обеспечивает математически строгий способ рассмотрения меры Винера как гауссовой меры в пространстве Соболева . ^[64] ${\displaystyle H^{1}([0,\infty ))}$

Восприятие цвета

Любой истинный физический цвет может быть представлен комбинацией чистых спектральных цветов . Поскольку физические цвета могут состоять из любого количества спектральных цветов, пространство физических цветов может быть удобно представлено гильбертовым пространством спектральных цветов. У людей есть три типа колбочек для восприятия цвета, поэтому воспринимаемые цвета могут быть представлены трехмерным евклидовым пространством. Линейное отображение «многие к одному» из гильбертова пространства физических цветов в евклидово пространство воспринимаемых человеком цветов объясняет, почему многие различные физические цвета могут восприниматься людьми как идентичные (например, чистый желтый свет по сравнению со смесью красного и зеленого цветов). свет, см. метамерия ). ^{[65] [66]}

Характеристики

Пифагорейская идентичность

Два вектора u и v в гильбертовом пространстве H ортогональны, когда ⟨ u , v ⟩ = 0 . Обозначение для этого: u ⊥ v . В более общем смысле, когда S является подмножеством в H , обозначение u ⊥ S означает, что u ортогонален каждому элементу из S.

Когда u и v ортогональны, имеем

$${\displaystyle \|u+v\|^{2}=\langle u+v,u+v\rangle =\langle u,u\rangle +2\,\operatorname {Re} \langle u,v\rangle +\langle v,v\rangle =\|u\|^{2}+\|v\|^{2}\,.}$$

Индукцией по n это распространяется на любое семейство u ₁ , ..., un из n _{ортогональных} векторов,

$${\displaystyle \left\|u_{1}+\cdots +u_{n}\right\|^{2}=\left\|u_{1}\right\|^{2}+\cdots +\left\|u_{n}\right\|^{2}.}$$

Хотя заявленное тождество Пифагора справедливо в любом пространстве внутреннего продукта, полнота необходима для расширения тождества Пифагора на серии. ^[67] Ряд Σ uk ортогональных _{векторов} сходится в H тогда и только тогда , когда сходится ряд квадратов норм и

$${\displaystyle {\Biggl \|}\sum _{k=0}^{\infty }u_{k}{\Biggr \|}^{2}=\sum _{k=0}^{\infty }\left\|u_{k}\right\|^{2}\,.}$$

Идентичность и поляризация параллелограмма

Геометрически тождество параллелограмма утверждает, что AC ² + BD ² = 2(AB ² + AD ² ) . Другими словами, сумма квадратов диагоналей в два раза больше суммы квадратов любых двух соседних сторон.

По определению, каждое гильбертово пространство также является банаховым пространством . Более того, в каждом гильбертовом пространстве имеет место следующее тождество параллелограмма : ^[68]

$${\displaystyle \|u+v\|^{2}+\|u-v\|^{2}=2{\bigl (}\|u\|^{2}+\|v\|^{2}{\bigr )}\,.}$$

И наоборот, каждое банахово пространство, в котором выполняется тождество параллелограмма, является гильбертовым пространством, а скалярное произведение однозначно определяется нормой с помощью поляризационного тождества . ^[69] Для вещественных гильбертовых пространств поляризационное тождество имеет вид

$${\displaystyle \langle u,v\rangle ={\tfrac {1}{4}}{\bigl (}\|u+v\|^{2}-\|u-v\|^{2}{\bigr )}\,.}$$

Для комплексных гильбертовых пространств это

$${\displaystyle \langle u,v\rangle ={\tfrac {1}{4}}{\bigl (}\|u+v\|^{2}-\|u-v\|^{2}+i\|u+iv\|^{2}-i\|u-iv\|^{2}{\bigr )}\,.}$$

Из закона параллелограмма следует, что любое гильбертово пространство является равномерно выпуклым банаховым пространством . ^[70]

Лучшее приближение

В этом подразделе используется теорема о проекции Гильберта . Если C — непустое замкнутое выпуклое подмножество гильбертова пространства H, а x — точка в H , то существует единственная точка y ∈ C , которая минимизирует расстояние между x и точками в C , ^[71]

$${\displaystyle y\in C\,,\quad \|x-y\|=\operatorname {dist} (x,C)=\min {\bigl \{}\|x-z\|\mathrel {\big |} z\in C{\bigr \}}\,.}$$

Это эквивалентно утверждению, что в сдвинутом выпуклом множестве D = C − x существует точка с минимальной нормой . Доказательство состоит в том, чтобы показать, что каждая минимизирующая последовательность ( d _n ) ⊂ D является Коши (с использованием тождества параллелограмма), следовательно, сходится (с использованием полноты) к точке в D , которая имеет минимальную норму. В более общем смысле это справедливо в любом равномерно выпуклом банаховом пространстве. ^[72]

Когда этот результат применяется к замкнутому подпространству F в H , можно показать, что точка y ∈ F , ближайшая к x , характеризуется ^[73]

$${\displaystyle y\in F\,,\quad x-y\perp F\,.}$$

Эта точка y является ортогональной проекцией x на F , а отображение P _F  : x → y линейно (см. Ортогональные дополнения и проекции) . Этот результат особенно важен в прикладной математике , особенно в численном анализе , где он лежит в основе методов наименьших квадратов . ^[74]

В частности, когда F не равно H , можно найти ненулевой вектор v, ортогональный F (выберите x ∉ F и v = x − y ). Очень полезный критерий получается применением этого наблюдения к замкнутому подпространству F , порожденному подмножеством S из H.

Подмножество S в H охватывает плотное векторное подпространство тогда и только тогда, когда вектор 0 является единственным вектором v ∈ H , ортогональным S .

Двойственность

Двойственное пространство H * — это пространство всех непрерывных линейных функций из пространства H в основное поле. Оно несет в себе естественную норму, определенную

$${\displaystyle \|\varphi \|=\sup _{\|x\|=1,x\in H}|\varphi (x)|\,.}$$

закону параллелограммаполяризацииe _• = ( e _i ) _{i ∈ I}H ${\displaystyle f,g\in H^{*}}$

$${\displaystyle \langle f,g\rangle _{H^{*}}=\sum _{i\in I}f(e_{i}){\overline {g(e_{i})}}}$$

Теорема о представлении Рисса дает удобное описание двойственного пространства. Каждому элементу u из H существует уникальный элемент φ _u из H * , определяемый формулой

$${\displaystyle \varphi _{u}(x)=\langle x,u\rangle }$$

${\displaystyle \left\|\varphi _{u}\right\|=\left\|u\right\|.}$

Теорема о представлении Рисса утверждает, что отображение H в H * , определяемое u ↦ φ _u , является сюръективным , что делает это отображение изометрическим антилинейным изоморфизмом. ^[75] Итак, для каждого элемента ф двойственного H * существует один и только один u _φ в H такой, что

$${\displaystyle \langle x,u_{\varphi }\rangle =\varphi (x)}$$

x ∈ H.H *

$${\displaystyle \langle \varphi ,\psi \rangle =\langle u_{\psi },u_{\varphi }\rangle \,.}$$

Изменение порядка в правой части восстанавливает линейность в φ из антилинейности u _φ . В реальном случае антилинейный изоморфизм H к его двойственному пространству на самом деле является изоморфизмом, и поэтому реальные гильбертовы пространства естественно изоморфны своим собственным двойственным пространствам.

Представляющий вектор u _φ получается следующим образом. Когда φ ≠ 0 , ядро ​​F = Ker( φ ) является замкнутым векторным подпространством H , не равным H , следовательно, существует ненулевой вектор v, ортогональный F . Вектор u является подходящим скалярным кратным λv вектора v . Требование, чтобы φ ( v ) = ⟨ v , u ⟩ , дает

$${\displaystyle u=\langle v,v\rangle ^{-1}\,{\overline {\varphi (v)}}\,v\,.}$$

Это соответствие φ ↔ u используется в популярных в физике обозначениях брекетов . ^[76] В физике принято предполагать, что скалярное произведение, обозначаемое ⟨ x | y ⟩ , линейна справа,

$${\displaystyle \langle x|y\rangle =\langle y,x\rangle \,.}$$

⟨ х | y ⟩⟨ x |бюстгальтер| y ⟩кет

Теорема о представлении Рисса фундаментально опирается не только на наличие скалярного произведения, но и на полноту пространства. Фактически, из теоремы следует, что топологическое двойственное пространство любого внутреннего продукта может быть отождествлено с его пополнением. ^[77] Непосредственным следствием теоремы о представлении Рисса является также то, что гильбертово пространство H рефлексивно , а это означает, что естественное отображение H в его двойное двойственное пространство является изоморфизмом.

Слабо сходящиеся последовательности

В гильбертовом пространстве H последовательность { x _n } слабо сходится к вектору x ∈ H , когда

$${\displaystyle \lim _{n}\langle x_{n},v\rangle =\langle x,v\rangle }$$

v ∈ H.

Например, любая ортонормированная последовательность { f _n } слабо сходится к 0, как следствие неравенства Бесселя. Любая слабо сходящаяся последовательность { xn } ограничена принципом равномерной _{ограниченности} .

Обратно, каждая ограниченная последовательность в гильбертовом пространстве допускает слабо сходящиеся подпоследовательности ( теорема Алаоглу ). ^[78] Этот факт можно использовать для доказательства результатов минимизации для непрерывных выпуклых функционалов , точно так же, как теорема Больцано–Вейерштрасса используется для непрерывных функций на R ^d . Среди нескольких вариантов есть одно простое утверждение: ^[79]

Если f  : H → R — выпуклая непрерывная функция такая, что f ( x ) стремится к +∞ , когда ‖ x ‖ стремится к ∞ , то f допускает минимум в некоторой точке x ₀ ∈ H .

Этот факт (и различные его обобщения) имеют основополагающее значение для прямых методов вариационного исчисления . Результаты минимизации выпуклых функционалов также являются прямым следствием несколько более абстрактного факта, что замкнутые ограниченные выпуклые подмножества в гильбертовом пространстве H слабо компактны , поскольку H рефлексивно. Существование слабо сходящихся подпоследовательностей является частным случаем теоремы Эберлейна–Шмулиана .

Свойства банахового пространства

Любое общее свойство банаховых пространств продолжает сохраняться и для гильбертовых пространств. Теорема об открытом отображении утверждает, что непрерывное сюръективное линейное преобразование одного банахова пространства в другое является открытым отображением, что означает, что оно отправляет открытые множества в открытые множества. Следствием является ограниченная обратная теорема о том, что непрерывная и биективная линейная функция из одного банахова пространства в другое является изоморфизмом (то есть непрерывным линейным отображением, обратное для которого также непрерывно). Эту теорему значительно проще доказать в случае гильбертовых пространств, чем в общих банаховых пространствах. ^[80] Теорема об открытом отображении эквивалентна теореме о замкнутом графике , которая утверждает, что линейная функция из одного банахова пространства в другое является непрерывной тогда и только тогда, когда ее график является замкнутым множеством . ^[81] В случае гильбертовых пространств это является основным при изучении неограниченных операторов (см. закрытый оператор ).

(Геометрическая) теорема Хана – Банаха утверждает, что замкнутое выпуклое множество можно отделить от любой точки вне его с помощью гиперплоскости гильбертова пространства. Это непосредственное следствие свойства наилучшего приближения: если y — элемент замкнутого выпуклого множества F, ближайший к x , то разделяющая гиперплоскость — это плоскость, перпендикулярная отрезку xy , проходящая через его середину. ^[82]

Операторы в гильбертовых пространствах

Ограниченные операторы

Непрерывные линейные операторы A  : H ₁ → H ₂ из гильбертова пространства H ₁ во второе гильбертово пространство H ₂ ограничены в том смысле, что они отображают ограниченные множества в ограниченные множества. ^[83] Обратно, если оператор ограничен, то он непрерывен. Пространство таких ограниченных линейных операторов имеет норму , норму оператора , заданную формулой

$${\displaystyle \lVert A\rVert =\sup {\bigl \{}\|Ax\|\mathrel {\big |} \|x\|\leq 1{\bigr \}}\,.}$$

Сумма и композиция двух ограниченных линейных операторов снова ограничены и линейны. Для y в H ₂ отображение, которое переводит x ∈ H ₁ в ⟨ Ax , y ⟩ , является линейным и непрерывным, и поэтому согласно теореме о представлении Рисса может быть представлено в виде

$${\displaystyle \left\langle x,A^{*}y\right\rangle =\langle Ax,y\rangle }$$

A * yH _{1ограниченный} линейныйA *: H2 _→ H1сопряженныйA.A ** = Aк A идентично транспонированиюA :² *  → H ₁ * из _A ,по ${\displaystyle \psi \in H_{2}^{*}}$ ${\displaystyle \psi \circ A\in H_{1}^{*}.}$

Множество B( H ) всех ограниченных линейных операторов на H (имеются в виду операторы H → H ) вместе с операциями сложения и композиции, нормой и присоединенной операцией представляет собой C*-алгебру , которая является разновидностью операторной алгебры .

Элемент A из B( H ) называется «самосопряженным» или «эрмитовым», если A * = A. Если A эрмитово и ⟨ Ax , x ⟩ ≥ 0 для каждого x , то A называется «неотрицательным», пишется A ≥ 0 ; если равенство имеет место только при x = 0 , то A называется «положительным». Множество самосопряженных операторов допускает частичный порядок , в котором A ≥ B , если A − B ≥ 0 . Если A имеет форму B * B для некоторого B , то A неотрицательно; если B обратим, то A положителен. Обратное также верно в том смысле, что для неотрицательного оператора A существует единственный неотрицательный квадратный корень B такой, что

$${\displaystyle A=B^{2}=B^{*}B\,.}$$

В смысле, уточненном спектральной теоремой , самосопряженные операторы можно с пользой рассматривать как «реальные» операторы. Элемент A из B( H ) называется нормальным, если A * A = AA * . Нормальные операторы распадаются на сумму самосопряженного оператора и мнимого кратного самосопряженного оператора.

$${\displaystyle A={\frac {A+A^{*}}{2}}+i{\frac {A-A^{*}}{2i}}}$$

Элемент U из B( H ) называется унитарным , если U обратим и его обратный равен U * . Это также можно выразить, потребовав, чтобы U принадлежало и ⟨ Ux , Uy ⟩ = ⟨ x , y ⟩ для всех x , y ∈ H. Унитарные операторы образуют группу по композиции, которая является группой изометрии H .

Элемент B( H ) компактен , если он переводит ограниченные множества в относительно компактные множества. Эквивалентно, ограниченный оператор T компактен, если для любой ограниченной последовательности { x _k } последовательность { Tx _k } имеет сходящуюся подпоследовательность. Многие интегральные операторы компактны и фактически определяют специальный класс операторов, известных как операторы Гильберта – Шмидта , которые особенно важны при изучении интегральных уравнений . Операторы Фредгольма отличаются от компактного оператора кратностью единицы и эквивалентно характеризуются как операторы с конечномерным ядром и коядром . Индекс фредгольмова оператора T определяется формулой

$${\displaystyle \operatorname {index} T=\dim \ker T-\dim \operatorname {coker} T\,.}$$

Индекс гомотопически инвариантен и играет глубокую роль в дифференциальной геометрии посредством теоремы об индексе Атьи – Зингера .

Неограниченные операторы

Неограниченные операторы также применимы в гильбертовых пространствах и имеют важные приложения в квантовой механике . ^[84] Неограниченный оператор T в гильбертовом пространстве H определяется как линейный оператор, область определения D ( T ) которого является линейным подпространством H. Часто область D ( T ) является плотным подпространством H , и в этом случае T известен как плотно определенный оператор .

Сопряженный к плотно определенному неограниченному оператору определяется по существу так же, как и для ограниченных операторов. Самосопряженные неограниченные операторы играют роль наблюдаемых в математической формулировке квантовой механики. Примерами самосопряженных неограниченных операторов в гильбертовом пространстве L2 ( R ) ^{являются} : ^[85]

• Подходящее расширение дифференциального оператора
  $${\displaystyle (Af)(x)=-i{\frac {\mathrm {d} }{\mathrm {d} x}}f(x)\,,}$$
  где i — мнимая единица, а f — дифференцируемая функция с компактным носителем.
• Оператор умножения на x :
  $${\displaystyle (Bf)(x)=xf(x)\,.}$$

Они соответствуют наблюдаемым импульсу и положению соответственно. Ни A , ни B не определены на всем пространстве H , поскольку в случае A производная не обязательно должна существовать, а в случае B функция произведения не обязательно должна быть интегрируемой с квадратом. В обоих случаях набор возможных аргументов образует плотные подпространства L ² ( R ) .

Конструкции

Прямые суммы

Два гильбертовых пространства H ₁ и H ₂ можно объединить в другое гильбертово пространство, называемое (ортогональной) прямой суммой [ ^86] и обозначаемое

$${\displaystyle H_{1}\oplus H_{2}\,,}$$

состоящий из набора всех упорядоченных пар ( x ₁ , x ₂ ) , где x _i ∈ H _i , i = 1, 2 , и скалярного произведения, определяемого формулой

$${\displaystyle {\bigl \langle }(x_{1},x_{2}),(y_{1},y_{2}){\bigr \rangle }_{H_{1}\oplus H_{2}}=\left\langle x_{1},y_{1}\right\rangle _{H_{1}}+\left\langle x_{2},y_{2}\right\rangle _{H_{2}}\,.}$$

В более общем смысле, если H _i — семейство гильбертовых пространств с индексом i ∈ I , то прямая сумма H _i , обозначаемая

$${\displaystyle \bigoplus _{i\in I}H_{i}}$$

$${\displaystyle x=(x_{i}\in H_{i}\mid i\in I)\in \prod _{i\in I}H_{i}}$$

декартовом произведении_iчто

$${\displaystyle \sum _{i\in I}\|x_{i}\|^{2}<\infty \,.}$$

Внутренний продукт определяется

$${\displaystyle \langle x,y\rangle =\sum _{i\in I}\left\langle x_{i},y_{i}\right\rangle _{H_{i}}\,.}$$

Каждое из H _i включено как замкнутое подпространство в прямую сумму всех H _i . Более того, H _i попарно ортогональны. Обратно, если в гильбертовом пространстве H существует система замкнутых подпространств Vi _, i ∈ I , которые попарно ортогональны и объединение которых плотно в H , то H канонически изоморфно прямой _сумме Vi . В этом случае H называется внутренней прямой суммой V _i . Прямая сумма (внутренняя или внешняя) также снабжена семейством ортогональных проекторов E _i на i- е прямое слагаемое H _i . Эти проекции представляют собой ограниченные самосопряженные идемпотентные операторы, удовлетворяющие условию ортогональности.

$${\displaystyle E_{i}E_{j}=0,\quad i\neq j\,.}$$

Спектральная теорема для компактных самосопряженных операторов в гильбертовом пространстве H утверждает, что H распадается в ортогональную прямую сумму собственных пространств оператора, а также дает явное разложение оператора как сумму проекций на собственные пространства. Прямая сумма гильбертовых пространств также появляется в квантовой механике как пространство Фока системы, содержащей переменное число частиц, где каждое гильбертово пространство в прямой сумме соответствует дополнительной степени свободы квантовомеханической системы. В теории представлений теорема Питера -Вейля гарантирует, что любое унитарное представление компактной группы в гильбертовом пространстве распадается как прямая сумма конечномерных представлений.

Тензорные продукты

Если x ₁ , y ₁ ∊ H ₁ и x ₂ , y ₂ ∊ H ₂ , то скалярное произведение на (обычном) тензорном произведении определяется следующим образом. Пусть на простых тензорах

$${\displaystyle \langle x_{1}\otimes x_{2},\,y_{1}\otimes y_{2}\rangle =\langle x_{1},y_{1}\rangle \,\langle x_{2},y_{2}\rangle \,.}$$

Затем эта формула расширяется по полуторалинейности до скалярного произведения на H ₁ ⊗ H ₂ . Гильбертово тензорное произведение H ₁ и H ₂ , иногда обозначаемое H ₁ H ₂ ${\displaystyle {\widehat {\otimes }}}$ , представляет собой гильбертово пространство, полученное путем дополнения H ₁ ⊗ H ₂ для метрики, связанной с этим скалярным произведением. ^[87]

Примером может служить гильбертово пространство L ² ([0, 1]) . Гильбертово тензорное произведение двух копий L ² ([0, 1]) изометрически и линейно изоморфно пространству L ² ([0, 1] ² ) функций, интегрируемых с квадратом на квадрате [0, 1] ² . Этот изоморфизм переводит простой тензор f ₁ ⊗ f ₂ в функцию

$${\displaystyle (s,t)\mapsto f_{1}(s)\,f_{2}(t)}$$

Этот пример типичен в следующем смысле. ^[88] Каждому простому тензорному произведению x ₁ ⊗ x ₂ соответствует оператор ранга один из H^*
₁в H ₂ , который отображает заданный x * ∈ H^*
₁как

$${\displaystyle x^{*}\mapsto x^{*}(x_{1})x_{2}\,.}$$

Это отображение, определенное на простых тензорах, продолжается до линейного отождествления между H ₁ ⊗ H ₂ и пространством операторов конечного ранга из H^*
₁до Н ₂ . Это продолжается до линейной изометрии гильбертова тензорного произведения H ₁ H ₂ ${\displaystyle {\widehat {\otimes }}}$ с гильбертовым пространством HS ( H^*
₁, H ₂ ) операторов Гильберта–Шмидта из H^*
₁до Н ₂ .

Ортонормированные базы

Понятие ортонормированного базиса из линейной алгебры обобщается на случай гильбертовых пространств. ^[89] В гильбертовом пространстве H ортонормированный базис — это семейство { e _k } _{k ∈ B} элементов H , удовлетворяющее условиям:

1. Ортогональность : каждые два разных элемента B ортогональны: ⟨ e _k , e _j ⟩ = 0 для всех k , j ∈ B , где k ≠ j .
2. Нормализация : Каждый элемент семейства имеет норму 1: ‖ e _k ‖ = 1 для всех k ∈ B .
3. Полнота : Линейная оболочка семейства ek , k ∈ B , плотна в H. _{_}

Система векторов, удовлетворяющая первым двум условиям базиса, называется ортонормированной системой или ортонормированным множеством (или ортонормированной последовательностью, если B счетно ) . Такая система всегда линейно независима .

Несмотря на название, ортонормированный базис, вообще говоря, не является базисом в смысле линейной алгебры ( базисом Гамеля ). Точнее, ортонормированный базис является базисом Гамеля тогда и только тогда, когда гильбертово пространство является конечномерным векторным пространством. ^[90]

Полноту ортонормированной системы векторов гильбертова пространства можно эквивалентно переформулировать как:

для каждого v ∈ H , если ⟨ v , e _k ⟩ = 0 для всех k ∈ B , то v = 0 .

Это связано с тем, что единственным вектором, ортогональным плотному линейному подпространству, является нулевой вектор, поскольку если S — любое ортонормированное множество и v ортогонально S , то v ортогонально замыканию линейной оболочки S , что это все пространство.

Примеры ортонормированных базисов включают:

• набор {(1, 0, 0), (0, 1, 0), (0, 0, 1)} образует ортонормированный базис R ³ со скалярным произведением ;
• последовательность {  f _n | n ∈ Z } с f _n ( x ) = exp (2π inx ) образует ортонормированный базис комплексного пространства L ² ([0, 1]) ;

В бесконечномерном случае ортонормированный базис не будет базисом в смысле линейной алгебры ; чтобы различать эти два базиса, последний базис также называют базисом Гамеля . Плотность диапазона базисных векторов означает, что каждый вектор в пространстве можно записать как сумму бесконечного ряда, а из ортогональности следует, что это разложение уникально.

Пространства последовательностей

Пространство суммируемых с квадратом последовательностей комплексных чисел представляет собой множество бесконечных последовательностей ^[9] ${\displaystyle \ell _{2}}$

$${\displaystyle (c_{1},c_{2},c_{3},\dots )}$$

$${\displaystyle \left|c_{1}\right|^{2}+\left|c_{2}\right|^{2}+\left|c_{3}\right|^{2}+\cdots <\infty \,.}$$

Это пространство имеет ортонормированный базис:

$${\displaystyle {\begin{aligned}e_{1}&=(1,0,0,\dots )\\e_{2}&=(0,1,0,\dots )\\&\ \ \vdots \end{aligned}}}$$

Это пространство является бесконечномерным обобщением пространства конечномерных векторов. Обычно это первый пример, используемый, чтобы показать, что в бесконечномерных пространствах замкнутое и ограниченное множество не обязательно (секвенциально) компактно (как это имеет место во всех конечномерных пространствах). Действительно, приведенный выше набор ортонормированных векторов показывает следующее: это бесконечная последовательность векторов в единичном шаре (т. е. шаре точек с нормой, меньшей или равной единице). Это множество явно ограничено и замкнуто; однако ни одна подпоследовательность этих векторов ни к чему не сходится, и, следовательно, единичный шар в не компактен. Интуитивно это происходит потому, что «всегда существует другое направление координат», в которое могут уйти следующие элементы последовательности. ${\displaystyle \ell _{2}^{n}}$ ${\displaystyle \ell _{2}}$

Обобщить пространство можно разными способами. Например, если B — любое множество, то можно сформировать гильбертово пространство последовательностей с набором индексов B , определенным в ^[91] ${\displaystyle \ell _{2}}$

$${\displaystyle \ell ^{2}(B)={\biggl \{}x:B\xrightarrow {x} \mathbb {C} \mathrel {\bigg |} \sum _{b\in B}\left|x(b)\right|^{2}<\infty {\biggr \}}\,.}$$

Суммирование по B здесь определяется формулой

$${\displaystyle \sum _{b\in B}\left|x(b)\right|^{2}=\sup \sum _{n=1}^{N}\left|x(b_{n})\right|^{2}}$$

граньBl ² ( B )

$${\displaystyle \langle x,y\rangle =\sum _{b\in B}x(b){\overline {y(b)}}}$$

для всех Икс , y ∈ л ² ( B ) . Здесь сумма также имеет только счетное число ненулевых членов и безоговорочно сходится по неравенству Коши – Шварца.

Ортонормированный базис l ² ( B ) индексируется множеством B , заданным формулой

$${\displaystyle e_{b}(b')={\begin{cases}1&{\text{if }}b=b'\\0&{\text{otherwise.}}\end{cases}}}$$

Неравенство Бесселя и формула Парсеваля

Пусть f ₁ , …, f _n — конечная ортонормированная система в  H . Для произвольного вектора x ∈ H пусть

$${\displaystyle y=\sum _{j=1}^{n}\langle x,f_{j}\rangle \,f_{j}\,.}$$

Тогда ⟨ x , f _k ⟩ = ⟨ y , f _k ⟩ для каждого k = 1, …, n . Отсюда следует, что x − y ортогонален каждому fk , следовательно _, x − y ортогонален  y . Дважды используя тождество Пифагора, следует, что

$${\displaystyle \|x\|^{2}=\|x-y\|^{2}+\|y\|^{2}\geq \|y\|^{2}=\sum _{j=1}^{n}{\bigl |}\langle x,f_{j}\rangle {\bigr |}^{2}\,.}$$

Пусть { f _i }, i ∈ I , — произвольная ортонормированная система в  H . Применение предыдущего неравенства к каждому конечному подмножеству J в I дает неравенство Бесселя: ^[92]

$${\displaystyle \sum _{i\in I}{\bigl |}\langle x,f_{i}\rangle {\bigr |}^{2}\leq \|x\|^{2},\quad x\in H}$$

произвольного семейства

Геометрически неравенство Бесселя означает, что ортогональная проекция x на линейное подпространство, натянутое на fi, имеет _норму , не превышающую норму x . В двух измерениях это утверждение, что длина катета прямоугольного треугольника не может превышать длину гипотенузы.

Неравенство Бесселя является ступенькой к более сильному результату, называемому тождеством Парсеваля , которое регулирует случай, когда неравенство Бесселя на самом деле является равенством. По определению, если { e _k } _{k ∈ B} является ортонормированным базисом H , то каждый элемент x из H можно записать как

$${\displaystyle x=\sum _{k\in B}\left\langle x,e_{k}\right\rangle \,e_{k}\,.}$$

Даже если B несчетно, неравенство Бесселя гарантирует, что выражение корректно определено и состоит только из счетного числа ненулевых членов. Эта сумма называется разложением Фурье x , а отдельные коэффициенты ⟨ x , e _k ⟩ являются коэффициентами Фурье x . Тогда тождество Парсеваля утверждает, что ^[93]

$${\displaystyle \|x\|^{2}=\sum _{k\in B}|\langle x,e_{k}\rangle |^{2}\,.}$$

Наоборот, ^[93] если { e _k } — ортонормированное множество такое, что тождество Парсеваля справедливо для каждого x , то { e _k } — ортонормированный базис.

Гильбертово измерение

Как следствие леммы Цорна , каждое гильбертово пространство допускает ортонормированный базис; более того, любые два ортонормированных базиса одного и того же пространства имеют одинаковую мощность , называемую гильбертовой размерностью пространства. ^[94] Например, поскольку l ² ( B ) имеет ортонормированный базис, индексированный B , его гильбертова размерность равна мощности B (которая может быть конечным целым числом или счетным или несчетным кардинальным числом ).

Гильбертова размерность не больше размерности Гамеля (обычной размерности векторного пространства). Два измерения равны тогда и только одно из них конечно.

Как следствие тождества Парсеваля ^[95] если { e _k } _{k ∈ B} является ортонормированным базисом H , то отображение Φ : H → l ² ( B ) , определенное формулой Φ( x ) = ⟨x, e _k ⟩ _{k ∈ B} — изометрический изоморфизм гильбертовых пространств: это биективное линейное отображение такое, что

$${\displaystyle {\bigl \langle }\Phi (x),\Phi (y){\bigr \rangle }_{l^{2}(B)}=\left\langle x,y\right\rangle _{H}}$$

x , y ∈ H.число—H. Таким образом ^,( B ) дляB.

Сепарабельные пространства

По определению, гильбертово пространство является сепарабельным , если оно содержит плотное счетное подмножество. Вместе с леммой Цорна это означает, что гильбертово пространство сепарабельно тогда и только тогда, когда оно допускает счетный ортонормированный базис. Таким образом, все бесконечномерные сепарабельные гильбертовы пространства изометрически изоморфны пространству суммируемых с квадратом последовательностей. ${\displaystyle \ell ^{2}.}$

Раньше в рамках определения часто требовалось, чтобы гильбертово пространство было отделимым. ^[96]

В квантовой теории поля

Большинство пространств, используемых в физике, являются сепарабельными, и, поскольку все они изоморфны друг другу, любое бесконечномерное сепарабельное гильбертово пространство часто называют « гильбертовым пространством» или просто «гильбертовым пространством». ^[97] Даже в квантовой теории поля большинство гильбертовых пространств на самом деле являются сепарабельными, как это предусмотрено аксиомами Вайтмана . Однако иногда утверждают, что несепарабельные гильбертовы пространства также важны в квантовой теории поля, примерно потому, что системы в теории обладают бесконечным числом степеней свободы и любым бесконечным гильбертовым тензорным произведением (пространств размерности больше единицы) является неразделимым. ^[98] Например, бозонное поле можно естественно рассматривать как элемент тензорного произведения, факторы которого представляют собой гармонические осцилляторы в каждой точке пространства. С этой точки зрения естественное пространство состояний бозона может показаться неразделимым пространством. ^[98] Однако только небольшое сепарабельное подпространство полного тензорного произведения может содержать физически значимые поля (на которых могут быть определены наблюдаемые). Другое несепарабельное гильбертово пространство моделирует состояние бесконечного набора частиц в неограниченной области пространства. Ортонормированный базис пространства индексируется плотностью частиц, непрерывным параметром, и поскольку множество возможных плотностей несчетно, базис не счетен. ^[98]

Ортогональные дополнения и проекции

Если S является подмножеством гильбертова пространства H , набор векторов, ортогональных S , определяется выражением

$${\displaystyle S^{\perp }=\left\{x\in H\mid \langle x,s\rangle =0\ {\text{ for all }}s\in S\right\}\,.}$$

Множество S ^⊥ является замкнутым подпространством в H (это легко доказать, используя линейность и непрерывность скалярного произведения) и поэтому образует гильбертово пространство. Если V — замкнутое подпространство H , то V ^⊥ называется ортогональным дополнением к V. Фактически, каждый x ∈ H тогда можно однозначно записать как x = v + w , где v ∈ V и w ∈ V ^⊥ . Следовательно, H — внутренняя прямая сумма Гильберта V и V ^⊥ .

Линейный оператор P _V  : H → H , который отображает x в v , называется ортогональным проектором на V. Существует естественное взаимно однозначное соответствие между множеством всех замкнутых подпространств в H и множеством всех ограниченных самосопряженных операторов P таких, что P ² = P . Конкретно,

Теорема  .  Ортогональный проектор P _V — это самосопряженный линейный оператор на H нормы ≤ 1 со свойством P²
_В= П _В . Более того, любой самосопряженный линейный оператор E такой, что E ² = E , имеет вид P _V , где V — образ E . Для каждого x в H PV ( x ) является уникальным элементом _v из V , который минимизирует расстояние ‖ x − v ‖ .

Это обеспечивает геометрическую интерпретацию PV ₍ x ) : это наилучшее приближение к x элементами V. ^[99]

Проекции P _U и P _V называются взаимно ортогональными, если P _U P _V = 0 . Это эквивалентно тому, что U и V ортогональны как подпространства H . Сумма двух проекций PU и PV является проекцией только в том случае, если _U и V ортогональны друг другу , _{и в этом} случае PU ₊ PV = PU _{+ V.} ^[100] Составной P _U P _V обычно не является проекцией; на самом деле, композиция является проекцией тогда и только тогда, когда две проекции коммутируют, и в этом случае P _U P _V = P _{U ∩ V} . ^[101]

Ограничивая кодобласть гильбертовым пространством V , ортогональная проекция PV приводит к отображению проекции _π  : H → V ; это сопряжение отображения включения

$${\displaystyle i:V\to H\,,}$$

$${\displaystyle \left\langle ix,y\right\rangle _{H}=\left\langle x,\pi y\right\rangle _{V}}$$

x ∈ Vy ∈ H.

Операторная норма ортогональной проекции P _V на ненулевое замкнутое подпространство V равна 1:

$${\displaystyle \|P_{V}\|=\sup _{x\in H,x\neq 0}{\frac {\|P_{V}x\|}{\|x\|}}=1\,.}$$

Поэтому каждое замкнутое подпространство V гильбертова пространства является образом оператора P нормы один такого, что P ² = P . Свойство наличия подходящих операторов проектирования характеризует гильбертово пространство: ^[102]

• Банахово пространство размерности выше 2 является (изометрически) гильбертовым пространством тогда и только тогда, когда для каждого замкнутого подпространства V существует оператор P _V нормы один, образ которого равен V , такой, что P²
  _В= П _В .

Хотя этот результат характеризует метрическую структуру гильбертова пространства, сама структура гильбертова пространства как топологического векторного пространства может быть охарактеризована с точки зрения наличия дополнительных подпространств: ^[103]

• Банахово пространство X топологически и линейно изоморфно гильбертовому пространству тогда и только тогда, когда для каждого замкнутого подпространства V существует замкнутое подпространство W такое, что X равно внутренней прямой сумме V ⊕ W .

Ортогональное дополнение удовлетворяет еще нескольким элементарным результатам. Это монотонная функция в том смысле, что если U ⊂ V , то V ^⊥ ⊆ U ^⊥ с равенством, выполняемым тогда и только тогда, когда V содержится в замыкании U . Этот результат является частным случаем теоремы Хана–Банаха . Замыкание подпространства можно полностью охарактеризовать в терминах ортогонального дополнения: если V — подпространство H , то замыкание V равно V ^⊥⊥ . Таким образом, ортогональное дополнение является связностью Галуа в частичном порядке подпространств гильбертова пространства. В общем, ортогональное дополнение суммы подпространств представляет собой пересечение ортогональных дополнений: ^[104]

$${\displaystyle {\biggl (}\sum _{i}V_{i}{\biggr )}^{\perp }=\bigcap _{i}V_{i}^{\perp }\,.}$$

Если V _i дополнительно замкнуты, то

$${\displaystyle {\overline {\sum _{i}V_{i}^{\perp }}}={\biggl (}\bigcap _{i}V_{i}{\biggr )}^{\perp }\,.}$$

Спектральная теория

Существует хорошо разработанная спектральная теория самосопряженных операторов в гильбертовом пространстве, которая примерно аналогична изучению симметричных матриц над действительными числами или самосопряженных матриц над комплексными числами. ^[105] В том же смысле можно получить «диагонализацию» самосопряженного оператора как подходящую сумму (фактически интеграл) ортогональных операторов проектирования.

Спектр оператора T , обозначаемый σ ( T ) , представляет собой набор комплексных чисел λ таких, что T − λ не имеет непрерывного обратного. Если T ограничено, то спектр всегда представляет собой компакт в комплексной плоскости и лежит внутри круга | г | ≤ ‖ Т ‖ . Если T самосопряженный, то спектр вещественный. Фактически он содержится в интервале [ m , M ] , где

$${\displaystyle m=\inf _{\|x\|=1}\langle Tx,x\rangle \,,\quad M=\sup _{\|x\|=1}\langle Tx,x\rangle \,.}$$

Более того, m и M фактически содержатся в спектре.

Собственные пространства оператора T задаются формулой

$${\displaystyle H_{\lambda }=\ker(T-\lambda )\,.}$$

В отличие от конечных матриц, не каждый элемент спектра T должен быть собственным значением: у линейного оператора T − λ может отсутствовать только обратный, поскольку он не является сюръективным. Элементы спектра оператора в общем смысле называются спектральными значениями . Поскольку спектральные значения не обязательно должны быть собственными значениями, спектральное разложение часто бывает более тонким, чем в конечных измерениях.

Однако спектральная теорема о самосопряженном операторе Т принимает особенно простой вид, если дополнительно предположить, что Т — компактный оператор . Спектральная теорема для компактных самосопряженных операторов гласит: ^[106]

• Компактный самосопряженный оператор T имеет лишь счетное (или конечное) число спектральных значений. Спектр T не имеет предельной точки в комплексной плоскости, кроме, возможно, нуля. Собственные пространства T разлагают H в ортогональную прямую сумму:
  $${\displaystyle H=\bigoplus _{\lambda \in \sigma (T)}H_{\lambda }\,.}$$
  Более того, если E _λ обозначает ортогональный проектор на собственное пространство H _λ , то
  $${\displaystyle T=\sum _{\lambda \in \sigma (T)}\lambda E_{\lambda }\,,}$$
  где сумма сходится по норме на B( H ) .

Эта теорема играет фундаментальную роль в теории интегральных уравнений , так как многие интегральные операторы компактны, в частности те, которые возникают из операторов Гильберта–Шмидта .

Общая спектральная теорема для самосопряженных операторов включает в себя своего рода операторнозначный интеграл Римана – Стилтьеса , а не бесконечное суммирование. ^[107] Спектральное семейство , связанное с T , сопоставляет каждому вещественному числу λ оператор E _λ , который является проекцией на нулевое пространство оператора ( T − λ ) ⁺ , где положительная часть самосопряженного оператора определяется формулой

$${\displaystyle A^{+}={\tfrac {1}{2}}{\Bigl (}{\sqrt {A^{2}}}+A{\Bigr )}\,.}$$

Операторы E _λ монотонно возрастают относительно частичного порядка, определенного на самосопряженных операторах; собственные значения в точности соответствуют разрывам скачка. Существует спектральная теорема, которая утверждает

$${\displaystyle T=\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{\lambda }\,.}$$

Под интегралом понимается интеграл Римана–Стилтьеса, сходящийся по норме на B( H ) . В частности, имеет место обычное скалярнозначное интегральное представление

$${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} \langle E_{\lambda }x,y\rangle \,.}$$

Несколько похожее спектральное разложение справедливо и для нормальных операторов, хотя, поскольку спектр теперь может содержать недействительные комплексные числа, вместо этого операторно-значную меру Стилтьеса d E _λ необходимо заменить разрешением тождества .

Важным применением спектральных методов является теорема о спектральном отображении , которая позволяет применить к самосопряженному оператору T любую непрерывную комплексную функцию f , определенную на спектре оператора T , путем формирования интеграла

$${\displaystyle f(T)=\int _{\sigma (T)}f(\lambda )\,\mathrm {d} E_{\lambda }\,.}$$

Полученное в результате непрерывное функциональное исчисление имеет приложения, в частности, к псевдодифференциальным операторам . ^[108]

Спектральная теория неограниченных самосопряженных операторов лишь немногим сложнее, чем ограниченных операторов. Спектр неограниченного оператора определяется точно так же, как и для ограниченных операторов: λ является спектральной величиной, если резольвентный оператор

$${\displaystyle R_{\lambda }=(T-\lambda )^{-1}}$$

не может быть корректно определенным непрерывным оператором. Самосопряженность T по-прежнему гарантирует вещественность спектра. Таким образом, основная идея работы с неограниченными операторами состоит в том, чтобы вместо этого рассматривать резольвенту R _λ , где λ недействителен. Это ограниченный нормальный оператор, допускающий спектральное представление, которое затем можно перевести в спектральное представление самого T. Похожая стратегия используется, например, для изучения спектра оператора Лапласа: вместо того, чтобы напрямую обращаться к оператору, вместо этого рассматривают связанную резольвенту, такую ​​​​как потенциал Рисса или потенциал Бесселя .

Точная версия спектральной теоремы в этом случае такова: ^[109]

Теорема  .  Данному плотно определенному самосопряженному оператору T в гильбертовом пространстве H соответствует единственное разрешение идентичности E на борелевских множествах R , такое, что

$${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{x,y}(\lambda )}$$

для всех x ∈ D ( T ) и y ∈ H . Спектральная мера E сосредоточена на спектре T .

Существует также версия спектральной теоремы, применимая к неограниченным нормальным операторам.

В популярной культуре

В романе Томаса Пинчона «Радуга гравитации» (1973) одного из персонажей зовут «Сэмми Гилберт-Спасс», игра слов на тему «Гильбертово пространство». В романе также упоминаются теоремы Гёделя о неполноте . ^[110]

Смотрите также

• Математический портал

• Банахово пространство  - полное нормированное векторное пространство.
• Пространство Фока  - Пространство многочастичных состояний.
• Основная теорема гильбертовых пространств
• Пространство Адамара  - геодезически полное метрическое пространство неположительной кривизны.Pages displaying wikidata descriptions as a fallback
• Пространство Хаусдорфа  - Тип топологического пространства.
• Гильбертова алгебра
• Гильберт C*-модуль  - Математические объекты, обобщающие понятие гильбертовых пространств.
• Гильбертово многообразие  - Многообразие, смоделированное на гильбертовых пространствах.
• L-полувнутренний продукт  - обобщение внутренних произведений, применимое ко всем нормированным пространствам.
• Локально выпуклое топологическое векторное пространство  - векторное пространство с топологией, определяемой выпуклыми открытыми множествами.
• Теория операторов  - Математическая область исследования
• Операторные топологии  - Топологии на множестве операторов в гильбертовом пространстве.
• Квантовое пространство состояний  - математическое пространство, представляющее физические квантовые системы.
• Оснащенное гильбертово пространство  - конструкция, связывающая изучение «связанных» и непрерывных собственных значений в функциональном анализе.
• Топологическое векторное пространство  - векторное пространство с понятием близости.

Примечания

1. В некоторых соглашениях внутренние продукты вместо этого линейны по своим вторым аргументам.
2. Собственные значения ядра Фредгольма:1/λ, стремящиеся к нулю.

Примечания

1. Экслер 2014, с. 164 §6.2
2. Однако в некоторых источниках конечномерные пространства с этими свойствами называются предгильбертовыми пространствами, оставляя термин «гильбертово пространство» для бесконечномерных пространств; см., например, Левитан 2001.
3. Марсден 1974, §2.8
4. Математический материал в этом разделе можно найти в любом хорошем учебнике по функциональному анализу, например, Дьедонне (1960), Хьюитт и Стромберг (1965), Рид и Саймон (1980) или Рудин (1987).
5. Шефер и Вольф 1999, стр. 122–202.
6. Дьедонне 1960, §6.2
7. Роман 2008, с. 327
8. Роман 2008, с. 330 Теорема 13.8.
9. Штейн и Шакарчи 2005, с. 163}}
10. Дьедонне 1960
11. В основном из работы Германа Грассмана , по настоянию Августа Фердинанда Мёбиуса (Boyer & Merzbach 1991, стр. 584–586). Первое современное аксиоматическое описание абстрактных векторных пространств в конечном итоге появилось в отчете Джузеппе Пеано 1888 года (Grattan-Guinness 2000, §5.2.2; O'Connor & Robertson 1996).
12. Подробный отчет об истории гильбертовых пространств можно найти у Бурбаки 1987.
13. Шмидт 1908 г.
14. Титчмарш 1946, §IX.1
15. Лебег, 1904. Более подробную информацию об истории теории интеграции можно найти у Бурбаки (1987) и Сакса (2005).
16. Бурбаки 1987.
17. Данфорд и Шварц 1958, §IV.16
18. В Данфорде и Шварце (1958, §IV.16) результат о том, что каждый линейный функционал на L ² [0,1] представлен интегрированием, совместно приписывается Фреше (1907) и Риссу (1907). Общий результат о том, что двойственное гильбертово пространство отождествляется с самим гильбертовым пространством, можно найти у Рисса (1934).
19. фон Нейман 1929.
20. Клайн 1972, с. 1092
21. Гильберт, Нордхайм и фон Нейман, 1927 г.
22. Вейль 1931.
23. Пруговечки 1981, стр. 1–10.
24. фон Нейман, 1932 г.
25. Перес 1993, стр. 79–99.
26. Мерфи 1990, с. 112
27. Мерфи 1990, с. 72
28. Халмос 1957, раздел 42.
29. Хьюитт и Стромберг 1965.
30. Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. «Глава 22». Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия «Прикладная математика». Том. 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Дуврские публикации. п. 773. ИСБН 978-0-486-61272-0. LCCN  64-60036. МР  0167642. LCCN  65-12253.
31. Берс, Джон и Шехтер 1981.
32. Джусти 2003.
33. Штейн 1970
34. Подробности можно найти у Warner (1983).
35. Общий справочник по пространствам Харди - книга Дюрен (1970).
36. Кранц 2002, §1.4
37. Кранц 2002, §1.5
38. Янг 1988, Глава 9.
39. Педерсен 1995, §4.4
40. Более подробную информацию о методах конечных элементов с этой точки зрения можно найти в Brenner & Scott (2005).
41. Брезис 2010, раздел 9.5.
42. Эванс 1998
43. Патрия (1996), главы 2 и 3
44. Эйнсидлер и Уорд (2011), Предложение 2.14.
45. Рид и Саймон 1980
46. Трактовка рядов Фурье с этой точки зрения доступна, например, у Рудина (1987) или Фолланда (2009).
47. Халмош 1957, §5
48. Бахман, Наричи и Бекенштейн 2000
49. Штейн и Вайс 1971, §IV.2.
50. Ланчос 1988, стр. 212–213.
51. Ланцос 1988, уравнение 4-3.10.
52. Классическим справочником по спектральным методам является Courant & Hilbert 1953. Более современный отчет - Reed & Simon 1975.
53. Кац 1966
54. фон Нейман 1955
55. Холево 2001, с. 17
56. Риффель и Полак 2011, с. 55
57. Перес 1993, с. 101
58. Перес 1993, стр. 73.
59. Нильсен и Чуанг 2000, стр. 90
60. Биллингсли (1986), с. 477, упр. 34.13}}
61. Стэплтон 1995
62. Хьюитт и Стромберг (1965), Упражнение 16.45.
63. Карацас и Шрив 2019, Глава 3
64. Строк (2011), Глава 8.
65. Герман Вейль (2009), «Разум и природа», Разум и природа: избранные труды по философии, математике и физике , Princeton University Press..
66. Бертье, М. (2020), «Геометрия восприятия цвета. Часть 2: воспринимаемые цвета из реальных квантовых состояний и пересказ Геринга», Журнал математической нейронауки , 10 (1): 14, doi : 10.1186/s13408-020- 00092-x , PMC 7481323 , PMID  32902776 .
67. Рид и Саймон 1980, Теорема 12.6.
68. Рид и Саймон 1980, с. 38
69. Янг 1988, с. 23.
70. Кларксон 1936.
71. Рудин 1987, Теорема 4.10.
72. Данфорд и Шварц 1958, II.4.29
73. Рудин 1987, Теорема 4.11.
74. Бланше, Жерар; Чарбит, Морис (2014). Цифровая обработка сигналов и изображений с использованием MATLAB . Том. 1 (Второе изд.). Нью-Джерси: Уайли. стр. 349–360. ISBN 978-1848216402.
75. Вайдманн 1980, Теорема 4.8.
76. Перес 1993, стр. 77–78.
77. Вайдманн (1980), Упражнение 4.11.
78. Вайдманн 1980, §4.5
79. Бутаццо, Джаквинта и Хильдебрандт 1998, Теорема 5.17.
80. Халмос 1982, Задача 52, 58.
81. Рудин 1973 г.
82. Тревес 1967, Глава 18
83. Общая ссылка на этот раздел - Рудин (1973), глава 12.
84. См. Пруговечки (1981), Рид и Саймон (1980, глава VIII) и Фолланд (1989).
85. Пруговечки 1981, III, §1.4
86. Данфорд и Шварц 1958, IV.4.17-18
87. Вайдманн 1980, §3.4
88. Кадисон и Рингроуз, 1983, Теорема 2.6.4.
89. Данфорд и Шварц 1958, §IV.4.
90. Роман 2008, с. 218
91. Рудин 1987, Определение 3.7.
92. О случае конечных множеств индексов см., например, Halmos 1957, §5. О бесконечных наборах индексов см. Weidmann 1980, теорема 3.6.
93. Hewitt & Stromberg (1965), Теорема 16.26.
94. Левитан 2001. Многие авторы, такие как Данфорд и Шварц (1958, §IV.4), называют это просто измерением. Если гильбертово пространство не является конечномерным, это не то же самое, что его размерность как линейного пространства (мощность базиса Гамеля).
95. Хьюитт и Стромберг (1965), Теорема 16.29.
96. Пруговечки 1981, I, §4.2
97. фон Нейман (1955) определяет гильбертово пространство через счетный гильбертовский базис, который представляет собой изометрический изоморфизм с l ² . Это соглашение до сих пор сохраняется в самых строгих трактовках квантовой механики; см., например, Собрино 1996, Приложение Б.
98. Streater & Wightman 1964, стр. 86–87.
99. Янг 1988, Теорема 15.3.
100. фон Нейман 1955, Теорема 16
101. фон Нейман 1955, Теорема 14
102. Какутани 1939 г.
103. Линденштраусс и Цафрири, 1971 г.
104. Халмос 1957, §12
105. Общее описание спектральной теории в гильбертовых пространствах можно найти в работе Рисса и Сз.-Надя (1990). Более сложное описание языка C*-алгебр содержится у Рудина (1973) или Кадисона и Рингроуза (1997).
106. См., например, Riesz & Sz.-Nagy (1990, глава VI) или Weidmann 1980, глава 7. Этот результат был уже известен Шмидту (1908) в случае операторов, возникающих из целочисленных ядер.
107. Рисс и Сз.-Надь 1990, §§107–108.
108. Шубин 1987 г.
109. Рудин 1973, Теорема 13.30.
110. Томас, Пинчон (1973). Радуга гравитации . Викинг Пресс. стр. 217, 275. ISBN. 978-0143039945.

Рекомендации

• Экслер, Шелдон (18 декабря 2014 г.), «Линейная алгебра сделана правильно» , Тексты для бакалавров по математике (3-е изд.), Springer Publishing (опубликовано в 2015 г.), стр. 296, ISBN 978-3-319-11079-0
• Бахман, Джордж; Наричи, Лоуренс; Бекенштейн, Эдвард (2000), Фурье и вейвлет-анализ , Universitext, Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-98899-3, МР  1729490.
• Берс, Липман ; Джон, Фриц ; Шехтер, Мартин (1981), Уравнения в частных производных , Американское математическое общество, ISBN 978-0-8218-0049-2.
• Биллингсли, Патрик (1986), Вероятность и мера , Уайли.
• Бурбаки, Николя (1986), Спектральные теории , Элементы математики, Берлин: Springer-Verlag, ISBN 978-0-201-00767-1.
• Бурбаки, Николя (1987), Топологические векторные пространства , Элементы математики, Берлин: Springer-Verlag, ISBN 978-3-540-13627-9.
• Бойер, Карл Бенджамин ; Мерцбах, Ута С (1991), История математики (2-е изд.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8.
• Бреннер, С.; Скотт, Р.Л. (2005), Математическая теория методов конечных элементов (2-е изд.), Springer, ISBN 978-0-387-95451-6.
• Брезис, Хаим (2010), Функциональный анализ, пространства Соболева и уравнения в частных производных , Спрингер.
• Бутаццо, Джузеппе; Джаквинта, Мариано; Хильдебрандт, Стефан (1998), Одномерные вариационные задачи , Оксфордская серия лекций по математике и ее приложениям, том. 15, издательство Clarendon Press, издательство Оксфордского университета, ISBN. 978-0-19-850465-8, МР  1694383.
• Кларксон, Дж. А. (1936), «Равномерно выпуклые пространства», Пер. амер. Математика. Соц. , 40 (3): 396–414, номер документа : 10.2307/1989630 , JSTOR  1989630..
• Курант, Ричард ; Гильберт, Дэвид (1953), Методы математической физики, Vol. Я , Интерсайенс.
• Дьедонне, Жан (1960), Основы современного анализа , Academic Press.
• Дирак, ПАМ (1930), Принципы квантовой механики , Оксфорд: Clarendon Press.
• Данфорд, Н.; Шварц, Дж. Т. (1958), Линейные операторы, части I и II , Wiley-Interscience.
• Дюрен, П. (1970), Теория H ^p -пространств , Нью-Йорк: Academic Press..
• Эйнзидлер, Манфред; Уорд, Томас (2011), Эргодическая теория с точки зрения теории чисел , Спрингер.
• Эванс, LC (1998), Уравнения в частных производных , Провиденс: Американское математическое общество, ISBN 0-8218-0772-2.
• Фолланд, Джеральд Б. (2009), Анализ Фурье и его применение (Перепечатка книги Уодсворта и Брукса / Коула, 1992 г.), Книжный магазин Американского математического общества, ISBN 978-0-8218-4790-9.
• Фолланд, Джеральд Б. (1989), Гармонический анализ в фазовом пространстве , Анналы математических исследований, том. 122, Издательство Принстонского университета, ISBN 978-0-691-08527-2.
• Фреше, Морис (1907), «Sur les ансамбли функций и линейные операции», CR Acad. наук. Париж , 144 : 1414–1416..
• Фреше, Морис (1904), «Sur les opérations linéaires», Труды Американского математического общества , 5 (4): 493–499, номер документа : 10.2307/1986278, JSTOR  1986278.
• Джусти, Энрико (2003), Прямые методы вариационного исчисления , World Scientific, ISBN 978-981-238-043-2.
• Граттан-Гиннесс, Айвор (2000), Поиск математических корней, 1870–1940 , Princeton Paperbacks, Princeton University Press , ISBN 978-0-691-05858-0, МР  1807717.
• Халмос, Пол (1957), Введение в гильбертово пространство и теорию спектральной множественности , Chelsea Pub. Ко
• Халмош, Пол (1982), Книга задач гильбертова пространства , Springer-Verlag, ISBN 978-0-387-90685-0.
• Хьюитт, Эдвин; Стромберг, Карл (1965), Реальный и абстрактный анализ , Нью-Йорк: Springer-Verlag.
• Гильберт, Дэвид ; Нордхайм, Лотар Вольфганг ; фон Нейман, Джон (1927), «Über die Grundlagen der Quantenmechanik», Mathematische Annalen , 98 : 1–30, doi : 10.1007/BF01451579, S2CID  120986758.
• Холево, Александр С. (2001), Статистическая структура квантовой теории , Конспект лекций по физике, Springer, ISBN 3-540-42082-7, OCLC  318268606.
• Кац, Марк (1966), «Можно ли услышать форму барабана?», American Mathematical Monthly , 73 (4, часть 2): 1–23, doi : 10.2307/2313748, JSTOR  2313748.
• Кэдисон, Ричард В.; Рингроуз, Джон Р. (1997), Основы теории операторных алгебр. Том. Я , Аспирантура по математике, вып. 15, Провиденс, Род-Айленд: Американское математическое общество , ISBN. 978-0-8218-0819-1, МР  1468229.
• Кэдисон, Ричард В.; Рингроуз, Джон Р. (1983), Основы теории операторных алгебр, Vol. I: Элементарная теория , Нью-Йорк: Academic Press, Inc.
• Карацас, Иоаннис; Шрив, Стивен (2019), Броуновское движение и стохастическое исчисление (2-е изд.), Springer, ISBN 978-0-387-97655-6

• Какутани, Шизуо (1939), «Некоторые характеристики евклидова пространства», Японский журнал математики , 16 : 93–97, doi : 10.4099/jjm1924.16.0_93 , MR  0000895.
• Клайн, Моррис (1972), Математическая мысль от древних до наших дней, Том 3 (3-е изд.), Oxford University Press (опубликовано в 1990 г.), ISBN 978-0-19-506137-6.
• Колмогоров Андрей ; Фомин, Сергей В. (1970), Вводный реальный анализ (пересмотренное английское издание, перевод Ричарда А. Сильвермана (1975), изд.), Dover Press, ISBN 978-0-486-61226-3.
• Кранц, Стивен Г. (2002), Теория функций нескольких комплексных переменных , Провиденс, Род-Айленд: Американское математическое общество , ISBN 978-0-8218-2724-6.
• Ланцос, Корнелиус (1988), Прикладной анализ (переиздание 1956 г., изд. Прентис-Холл), Dover Publications, ISBN 978-0-486-65656-4.
• Лебег, Анри (1904), «Уроки интеграции и исследования примитивных функций», Готье-Виллар.
• Левитан, Б.М. (2001) [1994], «Гильбертово пространство», Математическая энциклопедия , EMS Press.
• Линденштраусс, Дж.; Цафрири, Л. (1971), «О проблеме дополненных подпространств», Израильский журнал математики , 9 (2): 263–269, doi : 10.1007/BF02771592, ISSN  0021-2172, MR  0276734, S2CID  119575718.
• Марсден, Джерролд Э. (1974), Элементарный классический анализ , WH Freeman and Co., MR  0357693.
• Мерфи, Джеральд Дж. (1990), C *-алгебры и теория операторов , Academic Press, ISBN 0-12-511360-9.
• фон Нейман, Джон (1929), «Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren», Mathematische Annalen , 102 : 49–131, doi : 10.1007/BF01782338, S2CID  121249803.
• фон Нейман, Джон (1932), «Физические приложения эргодической гипотезы», Proc Natl Acad Sci USA , 18 (3): 263–266, Бибкод : 1932PNAS...18..263N, doi : 10.1073/pnas.18.3 .263 , JSTOR  86260, PMC  1076204 , PMID  16587674.
• фон Нейман, Джон (1955), Математические основы квантовой механики , Принстонские ориентиры в математике, перевод Бейера, Роберта Т., Princeton University Press (опубликовано в 1996 г.), ISBN 978-0-691-02893-4, МР  1435976.
• Нильсен, Майкл А .; Чуанг, Исаак Л. (2000), Квантовые вычисления и квантовая информация (1-е изд.), Кембридж: Cambridge University Press , ISBN 978-0-521-63503-5, OCLC  634735192.
• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (1996), «Абстрактные линейные пространства», Архив истории математики MacTutor , Университет Сент-Эндрюс
• Патрия, РК (1996), Статистическая механика (2-е изд.), Academic Press..
• Педерсен, Герт (1995), Анализ сейчас , Тексты для выпускников по математике, том. 118, Берлин, Нью-Йорк: Springer-Verlag , ISBN. 978-1-4612-6981-6, МР  0971256
• Перес, Ашер (1993), Квантовая теория: концепции и методы , Kluwer, ISBN 0-7923-2549-4, OCLC  28854083
• Пруговечки, Эдуард (1981), Квантовая механика в гильбертовом пространстве (2-е изд.), Дувр (опубликовано в 2006 г.), ISBN 978-0-486-45327-9.
• Рид, Майкл ; Саймон, Барри (1980), Функциональный анализ (том I из 4 томов) , Методы современной математической физики, Academic Press, ISBN 978-0-12-585050-6.
• Рид, Майкл ; Саймон, Барри (1975), Анализ Фурье, самосопряженность (том II из 4 томов) , Методы современной математической физики, Academic Press, ISBN 9780125850025.
• Риффель, Элеонора Г .; Полак, Вольфганг Х. (04 марта 2011 г.), Квантовые вычисления: нежное введение , MIT Press, ISBN 978-0-262-01506-6.
• Рис, Фридьес (1907), «Sur une espèce de Géométrie analytique des systèmes de fonctions sommables», CR Acad. наук. Париж , 144 : 1409–1411..
• Рис, Фридьес (1934), "Zur Theorie des Hilbertschen Raumes", Acta Sci. Математика. Сегед , 7 : 34–38..
• Рисс, Фридьес ; С.-Надь, Бела (1990), Функциональный анализ , Дувр, ISBN 978-0-486-66289-3.
• Роман, Стивен (2008), Продвинутая линейная алгебра , Тексты для выпускников по математике (Третье изд.), Springer, ISBN 978-0-387-72828-5
• Рудин, Уолтер (1973). Функциональный анализ . Международная серия по чистой и прикладной математике. Том. 25 (Первое изд.). Нью-Йорк, штат Нью-Йорк: McGraw-Hill Science/Engineering/Math . ISBN 9780070542259.
• Рудин, Уолтер (1987), Реальный и комплексный анализ , McGraw-Hill, ISBN 978-0-07-100276-9.
• Сакс, Станислав (2005), Теория интеграла (2-е изд. Дувра), Дувр, ISBN 978-0-486-44648-6; первоначально опубликовано Monografje Matematyczne , vol. 7, Варшава, 1937 г.
• Шефер, Хельмут Х .; Вольф, Манфред П. (1999). Топологические векторные пространства . ГТМ . Том. 8 (Второе изд.). Нью-Йорк, Нью-Йорк: Springer New York Выходные данные Springer. ISBN 978-1-4612-7155-0. ОСЛК  840278135.
• Шмидт, Эрхард (1908), «Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten», Rend. Цирк. Мат. Палермо , 25 : 63–77, номер документа : 10.1007/BF03029116, S2CID  120666844..
• Шубин, М.А. (1987), Псевдодифференциальные операторы и спектральная теория , Ряды Спрингера в советской математике, Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-13621-7, МР  0883081.
• Собрино, Луис (1996), Элементы нерелятивистской квантовой механики , Ривер Эдж, Нью-Джерси: World Scientific Publishing Co. Inc., Бибкод : 1996lnrq.book.....S, doi : 10.1142/2865, ISBN 978-981-02-2386-1, МР  1626401.
• Стэплтон, Джеймс (1995), Линейные статистические модели , Джон Уайли и сыновья..
• Стюарт, Джеймс (2006), Исчисление: концепции и контексты (3-е изд.), Томсон / Брукс / Коул.
• Стейн, Э. (1970), Сингулярные интегралы и свойства дифференцируемости функций , Princeton Univ. Пресса, ISBN 978-0-691-08079-6.
• Штейн, Элиас ; Вайс, Гвидо (1971), Введение в анализ Фурье в евклидовых пространствах , Принстон, Нью-Джерси: Princeton University Press, ISBN 978-0-691-08078-9.
• Штейн, Э; Шакарчи, Р. (2005), Реальный анализ, теория меры, интегрирование и гильбертовы пространства , Princeton University Press.
• Стритер, Рэй ; Вайтман, Артур (1964), PCT, спин, статистика и все такое , WA Benjamin, Inc..
• Струк, Дэниел (2011), Теория вероятностей: аналитический взгляд (2-е изд.), Cambridge University Press.
• Тешль, Джеральд (2009). Математические методы в квантовой механике; С приложениями к операторам Шрёдингера. Провиденс : Американское математическое общество . ISBN 978-0-8218-4660-5..
• Титчмарш, Эдвард Чарльз (1946), Расширение собственных функций, часть 1 , Оксфордский университет: Clarendon Press.
• Тревес, Франсуа (1967), Топологические векторные пространства, распределения и ядра , Academic Press.
• Уорнер, Франк (1983), Основы дифференцируемых многообразий и групп Ли , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-90894-6.
• Вайдманн, Иоахим (1980), Линейные операторы в гильбертовых пространствах , Тексты для аспирантов по математике, том. 68, Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-90427-6, МР  0566954.
• Вейль, Герман (1931), Теория групп и квантовая механика (английское издание 1950 г.), Dover Press, ISBN 978-0-486-60269-1.
• Янг, Николас (1988), Введение в гильбертово пространство , Cambridge University Press, ISBN 978-0-521-33071-8, Збл  0645.46024.

Внешние ссылки

• «Гильбертово пространство», Математическая энциклопедия , EMS Press , 2001 [1994]
• Гильбертово пространство в Mathworld
• 245B, примечания 5: Гильбертовы пространства Теренса Тао.