В математике сложная геометрия — это изучение геометрических структур и конструкций , возникающих из комплексных чисел или описываемых ими . В частности, комплексная геометрия занимается изучением таких пространств , как комплексные многообразия и комплексные алгебраические многообразия , функции нескольких комплексных переменных и голоморфные конструкции, такие как голоморфные векторные расслоения и когерентные пучки . Применение трансцендентных методов к алгебраической геометрии попадает в эту категорию вместе с более геометрическими аспектами комплексного анализа .
Сложная геометрия находится на пересечении алгебраической геометрии, дифференциальной геометрии и комплексного анализа и использует инструменты из всех трех областей. Из-за сочетания методов и идей из разных областей проблемы сложной геометрии часто оказываются более решаемыми и конкретными, чем в целом. Например, классификация комплексных многообразий и комплексных алгебраических многообразий с помощью программы минимальной модели и построение пространств модулей отличает эту область от дифференциальной геометрии, где классификация возможных гладких многообразий является значительно более сложной проблемой. Кроме того, дополнительная структура сложной геометрии позволяет, особенно в компактной среде, с большим успехом доказывать глобальные аналитические результаты, включая доказательство Шинг-Тунг Яу гипотезы Калаби , соответствия Хитчина-Кобаяши , неабелева соответствия Ходжа. и результаты существования метрик Кэлера–Эйнштейна и метрик Кэлера постоянной скалярной кривизны . Эти результаты часто возвращаются в сложную алгебраическую геометрию, и, например, недавно классификация многообразий Фано с использованием K-стабильности получила огромную пользу как от методов анализа, так и от чистой бирациональной геометрии .
Сложная геометрия имеет важные приложения в теоретической физике, где она важна для понимания конформной теории поля , теории струн и зеркальной симметрии . Это часто является источником примеров в других областях математики, в том числе в теории представлений , где обобщенные многообразия флагов могут быть изучены с использованием комплексной геометрии, приводящей к теореме Бореля-Вейля-Ботта , или в симплектической геометрии , где кэлеровы многообразия являются симплектическими, в римановых в геометрии , где комплексные многообразия предоставляют примеры экзотических метрических структур, таких как многообразия Калаби-Яу и гиперкэлеровы многообразия , а также в калибровочной теории , где голоморфные векторные расслоения часто допускают решения важных дифференциальных уравнений , возникающих из физики, таких как уравнения Янга-Миллса . Кроме того, сложная геометрия оказывает влияние на чистую алгебраическую геометрию, где аналитические результаты в сложной ситуации, такие как теория Ходжа кэлеровых многообразий, вдохновляют на понимание структур Ходжа для многообразий и схем , а также p-адическую теорию Ходжа , теория деформации для комплексных многообразий вдохновляет на понимание теория деформации схем и результаты о когомологиях комплексных многообразий вдохновили на формулировку гипотез Вейля и стандартных гипотез Гротендика . С другой стороны, результаты и методы из многих из этих областей часто возвращаются в сложную геометрию, и, например, достижения в области математики теории струн и зеркальной симметрии многое открыли о природе многообразий Калаби-Яу , которые, по прогнозам теоретиков струн, должны имеют структуру лагранжевых расслоений согласно гипотезе SYZ , а развитие теории Громова – Виттена симплектических многообразий привело к прогрессу в перечислительной геометрии комплексных многообразий.
Гипотеза Ходжа , одна из задач премии тысячелетия , является проблемой сложной геометрии. [1]

В широком смысле сложная геометрия связана с пространствами и геометрическими объектами , которые в некотором смысле моделируются на комплексной плоскости . Особенности комплексной плоскости и комплексного анализа одной переменной, такие как внутреннее понятие ориентируемости (то есть возможность последовательного поворота на 90 градусов против часовой стрелки в каждой точке комплексной плоскости) и жесткость голоморфных функций (т. , существование единственной комплексной производной подразумевает комплексную дифференцируемость всех порядков), как видно, проявляется во всех формах изучения комплексной геометрии. Например, каждое комплексное многообразие канонически ориентируемо, и определенная форма теоремы Лиувилля справедлива для компактных комплексных многообразий или проективных комплексных алгебраических многообразий.
Сложная геометрия по своему вкусу отличается от того, что можно было бы назвать реальной геометрией, изучением пространств, основанным на геометрических и аналитических свойствах прямой с действительными числами . Например, в то время как гладкие многообразия допускают разбиения единицы , наборы гладких функций, которые могут быть тождественно равными единице на некотором открытом множестве и тождественно нулю в другом месте, комплексные многообразия не допускают таких наборов голоморфных функций. Действительно, это проявление теоремы тождества , типичного результата комплексного анализа одной переменной. В некотором смысле новизна сложной геометрии может быть связана с этим фундаментальным наблюдением.
Верно, что каждое комплексное многообразие является, в частности, вещественным гладким многообразием. Это происходит потому, что комплексная плоскость , забыв о своей комплексной структуре, изоморфна вещественной плоскости . Однако сложная геометрия обычно не рассматривается как отдельная область дифференциальной геометрии — исследования гладких многообразий. В частности, теорема Серра GAGA гласит, что каждое проективное аналитическое многообразие на самом деле является алгебраическим многообразием , и изучение голоморфных данных об аналитическом многообразии эквивалентно изучению алгебраических данных.
Эта эквивалентность указывает на то, что комплексная геометрия в некотором смысле ближе к алгебраической геометрии , чем к дифференциальной геометрии . Другой пример, связанный с природой комплексной плоскости, состоит в том, что при комплексном анализе одной переменной особенности мероморфных функций легко описать. Напротив, возможное сингулярное поведение непрерывной действительнозначной функции охарактеризовать гораздо труднее. В результате этого можно легко изучать сингулярные пространства в комплексной геометрии, такие как сингулярные комплексные аналитические многообразия или сингулярные комплексные алгебраические многообразия, тогда как в дифференциальной геометрии часто избегают изучения сингулярных пространств.
На практике сложная геометрия находится на пересечении дифференциальной геометрии, алгебраической геометрии и анализа нескольких комплексных переменных , а сложный геометр использует инструменты из всех трех областей для изучения сложных пространств. Типичные направления интересов в сложной геометрии включают классификацию комплексных пространств, изучение прикрепленных к ним голоморфных объектов (таких как голоморфные векторные расслоения и когерентные пучки ), а также тесные связи между сложными геометрическими объектами и другими областями математики и физики.
Комплексная геометрия занимается изучением комплексных многообразий , а также комплексных алгебраических и комплексных аналитических многообразий . В этом разделе определены эти типы пространств и представлены отношения между ними.
Комплексное многообразие — это такое топологическое пространство , что:
Обратите внимание, что, поскольку каждый биголоморфизм является диффеоморфизмом и является изоморфизмом как вещественное векторное пространство для , каждое комплексное многообразие размерности является, в частности, гладким многообразием размерности , которое всегда является четным числом.
В отличие от комплексных многообразий, которые всегда гладкие, комплексная геометрия также связана с возможными сингулярными пространствами. Аффинное комплексное аналитическое многообразие — это такое подмножество , что около каждой точки существует открытая окрестность и набор конечного числа голоморфных функций таких, что . По соглашению мы также требуем, чтобы множество было неприводимым . Точка является особой , если матрица Якоби вектора голоморфных функций не имеет полного ранга при , и неособой в противном случае. Проективное комплексное аналитическое многообразие — это подмножество комплексного проективного пространства , которое точно так же локально задается нулями конечного набора голоморфных функций на открытых подмножествах .
Аналогичным образом можно определить аффинное комплексное алгебраическое многообразие как подмножество , локально заданное как нулевое множество конечного числа полиномов от комплексных переменных. Чтобы определить проективное комплексное алгебраическое многообразие , требуется, чтобы подмножество локально задавалось нулевым набором конечного числа однородных многочленов .
Чтобы определить общее комплексное алгебраическое или комплексное аналитическое многообразие, необходимо понятие локально окольцованного пространства . Комплексное алгебро-аналитическое многообразие — это локально окольцованное пространство , которое локально изоморфно как локально окольцованное пространство аффинному комплексному алгебро-аналитическому многообразию. В аналитическом случае обычно допускается иметь топологию, локально эквивалентную топологии подпространства благодаря отождествлению с открытыми подмножествами , тогда как в алгебраическом случае часто используется топология Зариского . Опять же, мы также по соглашению требуем, чтобы это локально окольцованное пространство было неприводимым.
Поскольку определение особой точки является локальным, определение, данное для аффинного аналитического/алгебраического многообразия, применимо к точкам любого комплексного аналитического или алгебраического многообразия. Множество точек многообразия, которые являются особыми, называется сингулярным локусом , обозначаемым , а дополнением является неособый или гладкий локус , обозначаемый . Мы говорим, что комплексное многообразие является гладким или неособым, если его место сингулярностей пусто. То есть, если он равен своему неособому локусу.
По теореме о неявной функции для голоморфных функций каждое комплексное многообразие является, в частности, неособым комплексным аналитическим многообразием, но, вообще говоря, не является аффинным или проективным. По теореме Серра GAGA каждое проективное комплексное аналитическое многообразие на самом деле является проективным комплексным алгебраическим многообразием. Когда комплексное многообразие неособо, оно является комплексным многообразием. В более общем смысле неособое множество любого комплексного многообразия представляет собой комплексное многообразие.
Комплексные многообразия можно изучать с точки зрения дифференциальной геометрии, благодаря чему они оснащены дополнительными геометрическими структурами, такими как риманова метрика или симплектическая форма . Чтобы эта дополнительная структура соответствовала сложной геометрии, необходимо обеспечить ее совместимость со сложной структурой в подходящем смысле. Кэлерово многообразие — это комплексное многообразие с римановой метрикой и симплектической структурой, совместимой с комплексной структурой. Каждое комплексное подмногообразие кэлерова многообразия является кэлером, и поэтому, в частности, каждое неособое аффинное или проективное комплексное многообразие является кэлером после ограничения стандартной эрмитовой метрики или метрики Фубини-Исследования соответственно .
Другие важные примеры кэлеровых многообразий включают римановы поверхности , поверхности K3 и многообразия Калаби – Яу .
Теорема Серра GAGA утверждает, что проективные комплексные аналитические многообразия на самом деле являются алгебраическими. Хотя это не совсем верно для аффинных многообразий, существует класс комплексных многообразий, которые действуют очень похоже на аффинные комплексные алгебраические многообразия, называемые многообразиями Штейна . Многообразие называется Штейном, если оно голоморфно выпукло и голоморфно отделимо (технические определения см. в статье о многообразиях Штейна). Однако можно показать, что это эквивалентно тому, чтобы быть комплексным подмногообразием для некоторого . Другой способ, которым многообразия Штейна похожи на аффинные комплексные алгебраические многообразия, заключается в том, что теоремы Картана A и B справедливы для многообразий Штейна.
Примеры многообразий Штейна включают некомпактные римановы поверхности и неособые аффинные комплексные алгебраические многообразия.
Специальным классом комплексных многообразий являются гиперкелеровы многообразия , которые являются римановыми многообразиями, допускающими три различные совместимые интегрируемые почти комплексные структуры , которые удовлетворяют кватернионным отношениям . Таким образом, гиперкэлеровы многообразия являются кэлеровыми многообразиями в трех различных отношениях и, следовательно, имеют богатую геометрическую структуру.
Примеры гиперкелеровых многообразий включают пространства ALE , поверхности K3 , пространства модулей расслоений Хиггса , колчанные многообразия и многие другие пространства модулей , возникающие из калибровочной теории и теории представлений .

Как уже упоминалось, особый класс кэлеровых многообразий составляют многообразия Калаби–Яу. Они задаются кэлеровыми многообразиями с тривиальным каноническим расслоением . Обычно определение многообразия Калаби – Яу также должно быть компактным. В этом случае доказательство Яу гипотезы Калаби подразумевает, что допускает кэлерову метрику с нулевой кривизной Риччи , и это можно рассматривать как эквивалентное определение Калаби – Яу.
Многообразия Калаби-Яу нашли применение в теории струн и зеркальной симметрии , где они используются для моделирования дополнительных шести измерений пространства-времени в 10-мерных моделях теории струн. Примерами многообразий Калаби–Яу являются эллиптические кривые , поверхности K3 и комплексные абелевы многообразия .
Комплексное многообразие Фано — это комплексное алгебраическое многообразие с обильным антиканоническим линейным расслоением (т. е. обильным). Многообразия Фано представляют значительный интерес в комплексной алгебраической геометрии и, в частности, в бирациональной геометрии , где они часто возникают в программе минимальной модели . Фундаментальные примеры многообразий Фано даются проективным пространством где , и гладкими гиперповерхностями степени меньше .
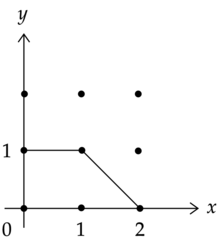
Торические многообразия — это комплексные алгебраические многообразия размерности , содержащие открытое плотное подмножество, биголоморфное , снабженное действием, расширяющим действие на открытое плотное подмножество. Торическое многообразие может быть описано комбинаторно с помощью его торического веера и, по крайней мере, если оно неособо, с помощью моментного многогранника . Это многоугольник, обладающий тем свойством, что любую вершину можно привести к стандартной форме вершины положительного ортанта действием . Торическое многообразие можно получить как подходящее пространство, расслояющееся на многогранник.
Многие конструкции, выполняемые на торических многообразиях, допускают альтернативные описания с точки зрения комбинаторики и геометрии моментного многогранника или связанного с ним торического веера. Это делает торические многообразия особенно привлекательным тестовым примером для многих конструкций сложной геометрии. Примеры торических многообразий включают комплексные проективные пространства и расслоения над ними.
Из-за жесткости голоморфных функций и комплексных многообразий методы, обычно используемые для изучения комплексных многообразий и комплексных многообразий, отличаются от методов, используемых в обычной дифференциальной геометрии, и ближе к методам, используемым в алгебраической геометрии. Например, в дифференциальной геометрии многие задачи решаются путем взятия локальных конструкций и их глобального объединения с использованием разбиений единицы. Разделов единства не существует в сложной геометрии, поэтому проблема того, когда локальные данные могут быть вклеены в глобальные данные, является более тонкой. Точное время, когда локальные данные могут быть объединены вместе, измеряется когомологиями пучков , а пучки и их группы когомологий являются основными инструментами.
Например, известными проблемами анализа нескольких комплексных переменных, предшествовавшими введению современных определений, являются проблемы Кузена , в которых точно задается вопрос, когда локальные мероморфные данные могут быть склеены для получения глобальной мероморфной функции. Эти старые проблемы можно просто решить после введения пучков и групп когомологий.
Специальные примеры пучков, используемых в сложной геометрии, включают голоморфные линейные расслоения (и связанные с ними дивизоры ), голоморфные векторные расслоения и когерентные пучки . Поскольку пучковые когомологии измеряют препятствия в сложной геометрии, одним из используемых методов является доказательство теорем об исчезновении. Примеры теорем об исчезновении в комплексной геометрии включают теорему об исчезновении Кодаиры для когомологий линейных расслоений на компактных кэлеровах многообразиях и теоремы Картана A и B для когомологий когерентных пучков на аффинных комплексных многообразиях.
В сложной геометрии также используются методы, возникшие на основе дифференциальной геометрии и анализа. Например, теорема Хирцебруха-Римана-Роха , частный случай теоремы Атьи-Зингера об индексе , вычисляет голоморфную эйлерову характеристику голоморфного векторного расслоения в терминах характеристических классов базового гладкого комплексного векторного расслоения.
Одной из основных тем сложной геометрии является классификация . Из-за жесткой природы комплексных многообразий и многообразий проблема классификации этих пространств часто решается. Классификация в сложной и алгебраической геометрии часто происходит посредством изучения пространств модулей , которые сами по себе являются комплексными многообразиями или многообразиями, точки которых классифицируют другие геометрические объекты, возникающие в сложной геометрии.
Термин «модули» был придуман Бернхардом Риманом во время его оригинальной работы над римановыми поверхностями. Теория классификации наиболее известна для компактных римановых поверхностей. По классификации замкнутых ориентированных поверхностей компактные римановы поверхности делятся на счетное число дискретных типов, измеряемых их родом , который представляет собой целое неотрицательное число, подсчитывающее количество дырок в данной компактной римановой поверхности.
Классификация по существу следует из теоремы об униформизации и выглядит следующим образом: [2] [3] [4]
Сложная геометрия касается не только комплексных пространств, но и других голоморфных объектов, присоединенных к ним. Классификация голоморфных линейных расслоений на комплексном многообразии задается многообразием Пикара .
Многообразие Пикара легко описать в случае, когда – компактная риманова поверхность рода g. А именно, в этом случае многообразие Пикара представляет собой непересекающееся объединение комплексных абелевых многообразий , каждое из которых изоморфно якобиану многообразия кривой, классифицирующее дивизоры нулевой степени с точностью до линейной эквивалентности. В дифференциально-геометрических терминах эти абелевы многообразия представляют собой комплексные торы, комплексные многообразия, диффеоморфные , возможно, с одной из многих различных комплексных структур.
По теореме Торелли компактная риманова поверхность определяется ее якобианом многообразием, и это демонстрирует одну из причин, почему изучение структур в комплексных пространствах может быть полезным, поскольку оно может позволить решить задачу классификации самих пространств.