Лагранжева механика

Формулировка классической механики

Жозеф-Луи Лагранж (1736–1813)

В физике , механика Лагранжа является формулировкой классической механики, основанной на принципе стационарного действия (также известном как принцип наименьшего действия). Он был введен итало-французским математиком и астрономом Жозефом-Луи Лагранжем в его презентации в Туринской академии наук в 1760 году ^[1] и достиг кульминации в его грандиозном труде 1788 года «Аналитическая механика» . ^[2]

Лагранжева механика описывает механическую систему как пару ( M , L ) , состоящую из конфигурационного пространства M и гладкой функции внутри этого пространства, называемой лагранжианом . Для многих систем L = T − V , где T и V — кинетическая и потенциальная энергия системы соответственно. ^[3] ${\textstyle L}$

Принцип стационарного действия требует, чтобы функционал действия системы, полученный из L , оставался в стационарной точке ( максимуме , минимуме или седле ) на протяжении всей временной эволюции системы. Это ограничение позволяет вычислять уравнения движения системы с использованием уравнений Лагранжа. ^[4]

Введение

Бусина ограничена движением по проводу без трения. Провод оказывает силу реакции C на бусинку, чтобы удерживать ее на проводе. Неограниченная сила N в этом случае — это гравитация. Обратите внимание, что начальное положение бусины на проводе может привести к различным движениям.

Простой маятник. Поскольку стержень жесткий, положение груза ограничено в соответствии с уравнением f ( x , y ) = 0 , сила ограничения C — это натяжение стержня. Опять же, неограничивающая сила N в этом случае — это сила тяжести.

Законы Ньютона и концепция сил являются обычной отправной точкой для обучения механическим системам. ^[5] Этот метод хорошо работает для многих задач, но для других подход оказывается кошмарно сложным. ^[6] Например, при расчете движения тора, катящегося по горизонтальной поверхности с жемчужиной, скользящей внутри, изменяющиеся во времени силы ограничения, такие как угловая скорость тора, движение жемчужины относительно тора, затрудняли определение движения тора с помощью уравнений Ньютона. ^[7] Лагранжева механика принимает энергию, а не силу в качестве своего основного ингредиента, ^[5] , что приводит к более абстрактным уравнениям, способным решать более сложные проблемы. ^[6]

В частности, подход Лагранжа заключался в установлении независимых обобщенных координат для положения и скорости каждого объекта, что позволяет записать общую форму лагранжиана (полная кинетическая энергия минус потенциальная энергия системы) и суммировать ее по всем возможным путям движения частиц, что дало формулу для «действия», которую он минимизировал, чтобы дать обобщенный набор уравнений. Эта суммированная величина минимизируется вдоль пути, который фактически проходит частица. Этот выбор устраняет необходимость в том, чтобы сила ограничения входила в результирующую обобщенную систему уравнений . Уравнений меньше, поскольку мы не вычисляем напрямую влияние ограничения на частицу в данный момент. ^[7]

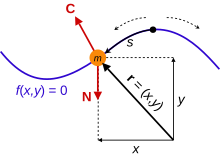
Для широкого спектра физических систем, если размер и форма массивного объекта пренебрежимо малы, полезным упрощением будет рассматривать его как точечную частицу . Для системы из N точечных частиц с массами m ₁ , m ₂ , ..., m _N каждая частица имеет вектор положения , обозначаемый r ₁ , r ₂ , ..., r _N . Часто бывает достаточно декартовых координат , поэтому r ₁ = ( x ₁ , y ₁ , z ₁ ) , r ₂ = ( x ₂ , y ₂ , z ₂ ) и так далее. В трехмерном пространстве каждый вектор положения требует трех координат для однозначного определения местоположения точки, поэтому существует 3 N координат для однозначного определения конфигурации системы. Все это конкретные точки в пространстве для определения местоположения частиц; общая точка в пространстве записывается как r = ( x , y , z ) . Скорость каждой частицы - это то, как быстро частица движется по своему пути движения, и является производной по времени от ее положения, таким образом, в ньютоновской механике уравнения движения задаются законами Ньютона . Второй закон "результирующая сила равна массе, умноженной на ускорение " применяется к каждой частице. Для системы из N частиц в 3 измерениях необходимо решить 3 N обыкновенных дифференциальных уравнений второго порядка относительно положений частиц. $${\displaystyle \mathbf {v} _{1}={\frac {d\mathbf {r} _{1}}{dt}},\mathbf {v} _{2}={\frac {d\mathbf {r} _{2}}{dt}},\ldots ,\mathbf {v} _{N}={\frac {d\mathbf {r} _{N}}{dt}}.}$$ $${\displaystyle \sum \mathbf {F} =m{\frac {d^{2}\mathbf {r} }{dt^{2}}},}$$

Лагранжиан

Вместо сил механика Лагранжа использует энергии в системе. Центральной величиной механики Лагранжа является лагранжиан , функция, которая суммирует динамику всей системы. В целом, лагранжиан имеет единицы энергии, но не имеет единого выражения для всех физических систем. Любая функция, которая генерирует правильные уравнения движения, в соответствии с физическими законами, может быть принята в качестве лагранжиана. Тем не менее, возможно построить общие выражения для больших классов приложений. Нерелятивистский лагранжиан для системы частиц в отсутствие электромагнитного поля определяется как ^[8] где — полная кинетическая энергия системы, равная сумме Σ кинетических энергий частиц . Каждая помеченная частица имеет массу , а v _k ² = v _k · v _k — квадрат ее скорости, эквивалентный скалярному произведению скорости на себя. ^[9] $${\displaystyle L=T-V,}$$ $${\displaystyle T={\frac {1}{2}}\sum _{k=1}^{N}m_{k}v_{k}^{2}}$$ ${\displaystyle N}$ ${\displaystyle k}$ ${\displaystyle m_{k},}$

Кинетическая энергия T — это энергия движения системы, которая является функцией только скоростей v _k , а не положений r _k или времени t , поэтому T = T ( v ₁ , v ₂ , ...).

V , потенциальная энергия системы, отражает энергию взаимодействия между частицами, т. е. сколько энергии имеет любая частица из-за всех остальных, вместе с любыми внешними воздействиями. Для консервативных сил (например, ньютоновской гравитации ) это функция только векторов положения частиц, поэтому V = V ( r ₁ , r ₂ , ...). Для тех неконсервативных сил, которые могут быть выведены из соответствующего потенциала (например, электромагнитного потенциала ), скорости также появятся, V = V ( r ₁ , r ₂ , ..., v ₁ , v ₂ , ...). Если есть некоторое внешнее поле или внешняя движущая сила, изменяющаяся со временем, потенциал изменяется со временем, поэтому в большинстве случаев V = V ( r ₁ , r ₂ , ..., v ₁ , v ₂ , ..., t ).

Как уже отмечалось, эта форма L применима ко многим важным классам систем, но не везде. Для релятивистской механики Лагранжа она должна быть заменена в целом функцией, согласующейся со специальной теорией относительности (скалярной относительно преобразований Лоренца) или общей теорией относительности (4-скалярной). ^[10] При наличии магнитного поля выражение для потенциальной энергии необходимо переформулировать. ^{[ требуется ссылка ]} А для диссипативных сил (например, трения ) должна быть введена еще одна функция наряду с Лагранжианом, часто называемая «функцией диссипации Рэлея», чтобы учесть потерю энергии. ^[11]

Одна или несколько частиц могут быть подвержены одному или нескольким голономным ограничениям ; такое ограничение описывается уравнением вида f ( r , t ) = 0. Если число ограничений в системе равно C , то каждое ограничение имеет уравнение f ₁ ( r , t ) = 0, f ₂ ( r , t ) = 0, ..., f _C ( r , t ) = 0, каждое из которых может применяться к любой из частиц. Если частица k подвержена ограничению i , то f _i ( rk , t ) = 0. В любой момент времени координаты ограниченной частицы связаны друг с другом и не являются независимыми. Уравнения ограничений определяют разрешенные пути, по которым могут двигаться частицы, но не то, _где они находятся или как быстро они движутся в каждый момент времени. Неголономные ограничения зависят от скоростей частиц, ускорений или высших производных положения. Лагранжева механика может быть применена только к системам, ограничения которых, если таковые имеются, являются голономными . Три примера неголономных ограничений: ^[12]

Когда уравнения ограничений неинтегрируемы, когда ограничения имеют неравенства или со сложными неконсервативными силами, такими как трение. Неголономные ограничения требуют специального рассмотрения, и может потребоваться вернуться к ньютоновской механике или использовать другие методы. ^[13]

Если T или V или оба явно зависят от времени из-за изменяющихся во времени ограничений или внешних воздействий, лагранжиан L ( r ₁ , r ₂ , ... v ₁ , v ₂ , ... t ) явно зависит от времени . Если ни потенциальная, ни кинетическая энергия не зависят от времени, то лагранжиан L ( r ₁ , r ₂ , ... v ₁ , v ₂ , ...) явно независим от времени . В любом случае лагранжиан всегда имеет неявную зависимость от времени через обобщенные координаты.

При этих определениях уравнения Лагранжа первого рода имеют вид ^[14]

Уравнения Лагранжа  (первый род)

${\displaystyle {\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0,}$

где k = 1, 2, ..., N обозначает частицы, для каждого уравнения ограничений f _i имеется множитель Лагранжа λ _i , и каждое из них является сокращением для вектора частных производных ∂/∂ по указанным переменным (не производной по всему вектору). ^{[nb 1]} Каждая точка сверху является сокращением для производной по времени . Эта процедура действительно увеличивает количество уравнений для решения по сравнению с законами Ньютона с 3 N до 3 N + C , поскольку имеется 3 N связанных дифференциальных уравнений второго порядка в координатах положения и множителях, плюс C уравнений ограничений. Однако при решении вместе с координатами положения частиц множители могут дать информацию о силах ограничений. Координаты не нужно исключать путем решения уравнений ограничений. $${\displaystyle {\frac {\partial }{\partial \mathbf {r} _{k}}}\equiv \left({\frac {\partial }{\partial x_{k}}},{\frac {\partial }{\partial y_{k}}},{\frac {\partial }{\partial z_{k}}}\right),\quad {\frac {\partial }{\partial {\dot {\mathbf {r} }}_{k}}}\equiv \left({\frac {\partial }{\partial {\dot {x}}_{k}}},{\frac {\partial }{\partial {\dot {y}}_{k}}},{\frac {\partial }{\partial {\dot {z}}_{k}}}\right)}$$

В лагранжиане координаты положения и компоненты скорости являются независимыми переменными , и производные лагранжиана берутся по ним отдельно в соответствии с обычными правилами дифференцирования (например, частная производная L по компоненту скорости z частицы 2, определяемая как v _{z ,2} = dz ₂ / dt , равна просто ∂ L /∂ v _{z ,2} ; не нужно использовать громоздкие цепные правила или полные производные, чтобы связать компонент скорости с соответствующей координатой z ₂ ).

В каждом уравнении ограничений одна координата является избыточной, поскольку она определяется из других координат. Число независимых координат, таким образом, равно n = 3 N − C . Мы можем преобразовать каждый вектор положения в общий набор n обобщенных координат , удобно записанный как n -кортеж q = ( q ₁ , q ₂ , ... q _n ) , выражая каждый вектор положения и, следовательно, координаты положения как функции обобщенных координат и времени: $${\displaystyle \mathbf {r} _{k}=\mathbf {r} _{k}(\mathbf {q} ,t)={\big (}x_{k}(\mathbf {q} ,t),y_{k}(\mathbf {q} ,t),z_{k}(\mathbf {q} ,t),t{\big )}.}$$

Вектор q является точкой в ​​конфигурационном пространстве системы. Производные по времени обобщенных координат называются обобщенными скоростями, и для каждой частицы преобразование ее вектора скорости, полной производной ее положения по времени, равно $${\displaystyle {\dot {q}}_{j}={\frac {\mathrm {d} q_{j}}{\mathrm {d} t}},\quad \mathbf {v} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}{\dot {q}}_{j}+{\frac {\partial \mathbf {r} _{k}}{\partial t}}.}$$

При этом v _k , кинетическая энергия в обобщенных координатах зависит от обобщенных скоростей, обобщенных координат и времени, если векторы положения явно зависят от времени из-за изменяющихся во времени ограничений, поэтому ${\displaystyle T=T(\mathbf {q} ,{\dot {\mathbf {q} }},t).}$

При этих определениях уравнения Эйлера–Лагранжа , или уравнения Лагранжа второго рода ^{[15] [16] [17]}

Уравнения Лагранжа  (второго рода)

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)={\frac {\partial L}{\partial q_{j}}}}$

являются математическими результатами из вариационного исчисления , которые также могут быть использованы в механике. Подстановка в лагранжиан L ( q , d q /d t , t ) дает уравнения движения системы. Количество уравнений уменьшилось по сравнению с ньютоновской механикой с 3 N до n = 3 N − C связанных дифференциальных уравнений второго порядка в обобщенных координатах. Эти уравнения вообще не включают в себя силы ограничений, необходимо учитывать только не связанные силы.

Хотя уравнения движения включают частные производные , результаты частных производных по-прежнему являются обычными дифференциальными уравнениями в координатах положения частиц. Полная производная по времени, обозначаемая d/d t, часто включает неявное дифференцирование . Оба уравнения линейны в лагранжиане, но, как правило, являются нелинейными связанными уравнениями в координатах.

От механики Ньютона к механике Лагранжа

законы Ньютона

Исаак Ньютон (1642–1727)

Для простоты законы Ньютона можно проиллюстрировать для одной частицы без особой потери общности (для системы из N частиц все эти уравнения применяются к каждой частице в системе). Уравнение движения для частицы постоянной массы m — это второй закон Ньютона 1687 года в современной векторной записи, где a — ее ускорение, а F — результирующая сила, действующая на нее. Когда масса меняется, уравнение необходимо обобщить, чтобы взять производную импульса по времени. В трех пространственных измерениях это система из трех связанных обыкновенных дифференциальных уравнений второго порядка для решения, поскольку в этом векторном уравнении есть три компонента. Решением является вектор положения r частицы в момент времени t , подчиняющийся начальным условиям r и v при t = 0. $${\displaystyle \mathbf {F} =m\mathbf {a} ,}$$

Законы Ньютона легко использовать в декартовых координатах, но декартовы координаты не всегда удобны, а для других систем координат уравнения движения могут усложняться. В наборе криволинейных координат ξ = ( ξ ¹ , ξ ² , ξ ³ ) закон в индексной записи тензора представляет собой «форму Лагранжа» ^{[18] [19]} , где F ^a — a -й контравариантный компонент результирующей силы, действующей на частицу, Γ ^a _bc — символы Кристоффеля второго рода, — кинетическая энергия частицы, а g _{bc —} ковариантные компоненты метрического тензора криволинейной системы координат. Все индексы a , b , c принимают значения 1, 2, 3. Криволинейные координаты — это не то же самое, что обобщенные координаты. $${\displaystyle F^{a}=m\left({\frac {\mathrm {d} ^{2}\xi ^{a}}{\mathrm {d} t^{2}}}+\Gamma ^{a}{}_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}\right)=g^{ak}\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\xi }}^{k}}}-{\frac {\partial T}{\partial \xi ^{k}}}\right),\quad {\dot {\xi }}^{a}\equiv {\frac {\mathrm {d} \xi ^{a}}{\mathrm {d} t}},}$$ $${\displaystyle T={\frac {1}{2}}mg_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}}$$

Может показаться, что это излишне усложняет формулировку закона Ньютона, но в этом есть свои преимущества. Компоненты ускорения в терминах символов Кристоффеля можно избежать, оценивая вместо этого производные кинетической энергии. Если на частицу не действует результирующая сила, F = 0 , она не ускоряется, а движется с постоянной скоростью по прямой. Математически решения дифференциального уравнения являются геодезическими , кривыми экстремальной длины между двумя точками в пространстве (они могут оказаться минимальными, то есть кратчайшими путями, но не обязательно). В плоском трехмерном реальном пространстве геодезические являются просто прямыми линиями. Таким образом, для свободной частицы второй закон Ньютона совпадает с геодезическим уравнением и гласит, что свободные частицы следуют геодезическим, экстремальным траекториям, по которым она может двигаться. Если частица подвергается воздействию сил F ≠ 0 , частица ускоряется из-за сил, действующих на нее, и отклоняется от геодезических, по которым она следовала бы, будучи свободной. При соответствующем расширении величин, приведенных здесь в плоском трехмерном пространстве, на четырехмерное искривленное пространство-время , приведенная выше форма закона Ньютона также переносится в общую теорию относительности Эйнштейна , в этом случае свободные частицы следуют геодезическим линиям в искривленном пространстве-времени, которые больше не являются «прямыми линиями» в обычном смысле. ^[20]

Однако нам все еще необходимо знать общую результирующую силу F, действующую на частицу, которая в свою очередь требует результирующей неограничивающей силы N плюс результирующей ограничивающей силы C , $${\displaystyle \mathbf {F} =\mathbf {C} +\mathbf {N} .}$$

Силы ограничений могут быть сложными, поскольку они, как правило, зависят от времени. Кроме того, если есть ограничения, криволинейные координаты не являются независимыми, а связаны одним или несколькими уравнениями ограничений.

Ограничительные силы можно либо исключить из уравнений движения, оставив только неограничительные силы, либо включить их, включив ограничительные уравнения в уравнения движения.

Принцип Даламбера

Жан д'Аламбер (1717—1783)

Сила ограничения C и виртуальное смещение δ r для частицы массы m, ограниченной кривой. Результирующая сила без ограничения равна N.

Фундаментальным результатом аналитической механики является принцип Даламбера , введенный в 1708 году Жаком Бернулли для понимания статического равновесия и развитый Даламбером в 1743 году для решения динамических задач. ^[21] Принцип утверждает, что для N частиц виртуальная работа, т. е. работа вдоль виртуального смещения, δ r _k , равна нулю: ^[9] $${\displaystyle \sum _{k=1}^{N}(\mathbf {N} _{k}+\mathbf {C} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0.}$$

Виртуальные смещения , δ r _k , по определению являются бесконечно малыми изменениями в конфигурации системы, согласующимися с силами ограничений, действующими на систему в момент времени , ^[22] т.е. таким образом, что силы ограничений поддерживают ограниченное движение. Они не совпадают с фактическими смещениями в системе, которые вызваны результирующими силами ограничений и силами без ограничений, действующими на частицу для ее ускорения и перемещения. ^{[nb 2]} Виртуальная работа — это работа, выполняемая вдоль виртуального смещения для любой силы (ограниченной или неограничительной).

Поскольку силы ограничения действуют перпендикулярно движению каждой частицы в системе для поддержания ограничений, общая виртуальная работа сил ограничения, действующих на систему, равна нулю: ^{[23] [nb 3]} так что $${\displaystyle \sum _{k=1}^{N}\mathbf {C} _{k}\cdot \delta \mathbf {r} _{k}=0,}$$ $${\displaystyle \sum _{k=1}^{N}(\mathbf {N} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0.}$$

Таким образом, принцип Даламбера позволяет нам сосредоточиться только на приложенных неограничивающих силах и исключить ограничивающие силы из уравнений движения. ^{[24] [25]} Показанная форма также не зависит от выбора координат. Однако ее нельзя легко использовать для составления уравнений движения в произвольной системе координат, поскольку смещения δ r _k могут быть связаны уравнением связи, что не позволяет нам приравнять N отдельных слагаемых к 0. Поэтому мы будем искать систему взаимно независимых координат, для которой общая сумма будет равна 0 тогда и только тогда, когда отдельные слагаемые равны 0. Приравнивание каждого из слагаемых к 0 в конечном итоге даст нам наши разделенные уравнения движения.

Уравнения движения из принципа Даламбера

Если есть ограничения на частицу k , то поскольку координаты положения r _k = ( x _k , y _k , z _k ) связаны между собой уравнением связи, то же самое касается и виртуальных перемещений δ r _k = ( δx _k , δy _k , δz _k ) . Поскольку обобщенные координаты независимы, мы можем избежать осложнений с δ r _{k ,} преобразуя обобщенные координаты в виртуальные перемещения. Они связаны в той же форме, что и полный дифференциал , ^[9] $${\displaystyle \delta \mathbf {r} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}.}$$

Не существует частной производной по времени относительно времени, умноженного на приращение времени, поскольку это виртуальное смещение, вдоль ограничений в момент времени .

Первый член в вышеприведенном принципе Даламбера представляет собой виртуальную работу, совершаемую не связанными силами N _k вдоль виртуальных перемещений δ r _k , и может без потери общности быть преобразован в обобщенные аналоги с помощью определения обобщенных сил , так что $${\displaystyle Q_{j}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}},}$$ $${\displaystyle \sum _{k=1}^{N}\mathbf {N} _{k}\cdot \delta \mathbf {r} _{k}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot \sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}=\sum _{j=1}^{n}Q_{j}\delta q_{j}.}$$

Это половина преобразования в обобщенные координаты. Остается преобразовать член ускорения в обобщенные координаты, что не сразу очевидно. Вспоминая форму Лагранжа второго закона Ньютона, можно найти частные производные кинетической энергии по обобщенным координатам и скоростям, что даст желаемый результат: ^[9] $${\displaystyle \sum _{k=1}^{N}m_{k}\mathbf {a} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}.}$$

Теперь принцип Даламбера в обобщенных координатах, как и требуется, и поскольку эти виртуальные смещения δq _j независимы и не равны нулю, коэффициенты можно приравнять к нулю, что приведет к уравнениям Лагранжа ^{[26] [27]} или обобщенным уравнениям движения , ^[28] $${\displaystyle \sum _{j=1}^{n}\left[Q_{j}-\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right)\right]\delta q_{j}=0,}$$ $${\displaystyle Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}}$$

Эти уравнения эквивалентны законам Ньютона для неограничивающих сил . Обобщенные силы в этом уравнении выводятся только из неограничивающих сил – ограничивающие силы были исключены из принципа Даламбера и не нуждаются в нахождении. Обобщенные силы могут быть неконсервативными, если они удовлетворяют принципу Даламбера. ^[29]

Уравнения Эйлера–Лагранжа и принцип Гамильтона

По мере развития системы q прокладывает путь через конфигурационное пространство (показаны только некоторые из них). Путь, пройденный системой (красный), имеет стационарное действие (δ S = 0) при небольших изменениях конфигурации системы (δ q ). ^[30]

Для неконсервативной силы, зависящей от скорости, может быть возможно найти функцию потенциальной энергии V , зависящую от положений и скоростей. Если обобщенные силы Q _i могут быть выведены из потенциала V таким образом, что ^{[31] [32]} приравнивание к уравнениям Лагранжа и определение лагранжиана как L = T − V дает уравнения Лагранжа второго рода или уравнения движения Эйлера–Лагранжа $${\displaystyle Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial V}{\partial {\dot {q}}_{j}}}-{\frac {\partial V}{\partial q_{j}}},}$$ $${\displaystyle {\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}=0.}$$

Однако уравнения Эйлера–Лагранжа могут учитывать неконсервативные силы только в том случае, если потенциал может быть найден, как показано. Это не всегда возможно для неконсервативных сил, и уравнения Лагранжа не включают в себя никакого потенциала, только обобщенные силы; поэтому они более общие, чем уравнения Эйлера–Лагранжа.

Уравнения Эйлера–Лагранжа также следуют из вариационного исчисления . Вариация лагранжиана имеет вид, аналогичный полному дифференциалу L , но виртуальные перемещения и их производные по времени заменяют дифференциалы, и нет никакого приращения времени в соответствии с определением виртуальных перемещений. Интегрирование по частям по времени может перевести производную по времени от δq _j в ∂ L /∂(d q _j /d t ), в процессе заменяя d( δq _j )/d t на δq j _, позволяя факторизовать независимые виртуальные перемещения из производных лагранжиана, $${\displaystyle \delta L=\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta {\dot {q}}_{j}\right),\quad \delta {\dot {q}}_{j}\equiv \delta {\frac {\mathrm {d} q_{j}}{\mathrm {d} t}}\equiv {\frac {\mathrm {d} (\delta q_{j})}{\mathrm {d} t}},}$$ $${\displaystyle {\begin{aligned}\int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t&=\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)\,\mathrm {d} t\\&=\sum _{j=1}^{n}\left[{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)\delta q_{j}\,\mathrm {d} t.\end{aligned}}}$$

Теперь, если условие δq _j ( t ₁ ) = δq _j ( t ₂ ) = 0 выполняется для всех j , неинтегрированные члены равны нулю. Если вдобавок весь временной интеграл δL равен нулю, то, поскольку δq _j независимы, и единственный способ для определенного интеграла быть равным нулю — это если подынтегральное выражение равно нулю, каждый из коэффициентов δq j _также должен быть равен нулю. Тогда мы получаем уравнения движения. Это можно обобщить с помощью принципа Гамильтона : $${\displaystyle \int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t=0.}$$

Интеграл по времени от лагранжиана — это еще одна величина, называемая действием , определяемая как ^[33], которая является функционалом ; она принимает функцию Лагранжа для всех времен между t ₁ и t ₂ и возвращает скалярное значение. Ее размерности такие же, как [ угловой момент ], [энергия]·[время] или [длина]·[импульс]. С этим определением принцип Гамильтона выглядит так: $${\displaystyle S=\int _{t_{1}}^{t_{2}}L\,\mathrm {d} t,}$$ $${\displaystyle \delta S=0.}$$

Вместо того, чтобы думать о частицах, ускоряющихся в ответ на приложенные силы, можно думать о них, выбирающих путь со стационарным действием, с конечными точками пути в конфигурационном пространстве, удерживаемыми фиксированными в начальный и конечный моменты времени. Принцип Гамильтона является одним из нескольких принципов действия . ^[34]

Исторически идея нахождения кратчайшего пути, по которому может следовать частица под действием силы, мотивировала первые применения вариационного исчисления к механическим проблемам, таким как задача о брахистохроне, решенная Жаном Бернулли в 1696 году, а также Лейбницем , Даниилом Бернулли , Лопиталем примерно в то же время и Ньютоном в следующем году. ^[35] Сам Ньютон размышлял в русле вариационного исчисления, но не публиковал свои идеи. ^[35] Эти идеи, в свою очередь, привели к вариационным принципам механики Ферма , Мопертюи , Эйлера , Гамильтона и других.

Принцип Гамильтона может быть применен к неголономным связям , если уравнения связей можно привести к определенной форме, линейной комбинации дифференциалов первого порядка в координатах. Полученное уравнение связей можно переформулировать в дифференциальное уравнение первого порядка. ^[36] Здесь это не будет приведено.

Множители Лагранжа и ограничения

Лагранжиан L можно варьировать в декартовых координатах r _k для N частиц, $${\displaystyle \int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0.}$$

Принцип Гамильтона по-прежнему действителен, даже если координаты L , выраженные в , не являются независимыми, здесь r _k , но ограничения по-прежнему предполагаются голономными. ^[37] Как всегда, конечные точки фиксированы δ r _k ( t ₁ ) = δ r _k ( t ₂ ) = 0 для всех k . Чего нельзя сделать, так это просто приравнять коэффициенты δ r _k к нулю, поскольку δ r _k не являются независимыми. Вместо этого можно использовать метод множителей Лагранжа для включения ограничений. Умножение каждого уравнения ограничений f _i ( r _k , t ) = 0 на множитель Лагранжа λ _i для i = 1, 2, ..., C и добавление результатов к исходному лагранжиану дает новый лагранжиан $${\displaystyle L'=L(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,{\dot {\mathbf {r} }}_{1},{\dot {\mathbf {r} }}_{2},\ldots ,t)+\sum _{i=1}^{C}\lambda _{i}(t)f_{i}(\mathbf {r} _{k},t).}$$

Множители Лагранжа являются произвольными функциями времени t , но не функциями координат r _k , поэтому множители равноправны с координатами положения. Изменение этого нового лагранжиана и интегрирование по времени дает $${\displaystyle \int _{t_{1}}^{t_{2}}\delta L'\mathrm {d} t=\int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0.}$$

Введенные множители можно найти так, чтобы коэффициенты δ r _k были равны нулю, даже если r _k не являются независимыми. Уравнения движения следуют. Из предыдущего анализа получение решения этого интеграла эквивалентно утверждению , которое является уравнениями Лагранжа первого рода . Кроме того, уравнения Эйлера-Лагранжа λ _i для нового лагранжиана возвращают уравнения связей $${\displaystyle {\frac {\partial L'}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\mathbf {r} }}_{k}}}=0\quad \Rightarrow \quad {\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0,}$$ $${\displaystyle {\frac {\partial L'}{\partial \lambda _{i}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\lambda }}_{i}}}=0\quad \Rightarrow \quad f_{i}(\mathbf {r} _{k},t)=0.}$$

Для случая консервативной силы, заданной градиентом некоторой потенциальной энергии V , функции только координат r _k , подстановка лагранжиана L = T − V дает и идентифицирует производные кинетической энергии как (отрицательную) результирующую силу, а производные потенциала равны неограничивающей силе, из этого следует, что ограничивающие силы, таким образом, явно задают ограничивающие силы в терминах уравнений связей и множителей Лагранжа. $${\displaystyle \underbrace {{\frac {\partial T}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\mathbf {r} }}_{k}}}} _{-\mathbf {F} _{k}}+\underbrace {-{\frac {\partial V}{\partial \mathbf {r} _{k}}}} _{\mathbf {N} _{k}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0,}$$ $${\displaystyle \mathbf {C} _{k}=\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}},}$$

Свойства лагранжиана

Неуникальность

Лагранжиан данной системы не является уникальным. Лагранжиан L можно умножить на ненулевую константу a и сдвинуть на произвольную константу b , и новый лагранжиан L ′ = aL + b будет описывать то же движение, что и L . Если ограничиться, как указано выше, траекториями q на заданном интервале времени [ t _st , t _fin ] } и фиксированными конечными точками P _st = q ( t _st ) и P _fin = q ( t _fin ) , то два лагранжиана, описывающих одну и ту же систему, могут отличаться на «полную производную по времени» функции f ( q , t ) : ^[38] где означает $${\displaystyle L'(\mathbf {q} ,{\dot {\mathbf {q} }},t)=L(\mathbf {q} ,{\dot {\mathbf {q} }},t)+{\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}},}$$ ${\textstyle {\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}}}$ ${\textstyle {\frac {\partial f(\mathbf {q} ,t)}{\partial t}}+\sum _{i}{\frac {\partial f(\mathbf {q} ,t)}{\partial q_{i}}}{\dot {q}}_{i}.}$

Оба лагранжиана L и L ′ производят одни и те же уравнения движения ^{[39] [40]} , поскольку соответствующие действия S и S ′ связаны через последние два компонента f ( P _fin , t _fin ) и f ( P _st , t _st ), не зависящие от q . $${\displaystyle {\begin{aligned}S'[\mathbf {q} ]&=\int _{t_{\text{st}}}^{t_{\text{fin}}}L'(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt\\&=\int _{t_{\text{st}}}^{t_{\text{fin}}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt+\int _{t_{\text{st}}}^{t_{\text{fin}}}{\frac {\mathrm {d} f(\mathbf {q} (t),t)}{\mathrm {d} t}}\,dt\\&=S[\mathbf {q} ]+f(P_{\text{fin}},t_{\text{fin}})-f(P_{\text{st}},t_{\text{st}}),\end{aligned}}}$$

Инвариантность относительно точечных преобразований

Если задан набор обобщенных координат q , то если мы заменим эти переменные на новый набор обобщенных координат Q в соответствии с точечным преобразованием Q = Q ( q , t ) , которое обратимо при q = q ( Q , t ) , то новый лагранжиан L ′ будет функцией новых координат , и по правилу цепочки для частного дифференцирования уравнения Лагранжа будут инвариантны относительно этого преобразования; ^[41] $${\displaystyle L'(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=L(\mathbf {q} (\mathbf {Q} ,t),{\dot {\mathbf {q} }}(\mathbf {Q} ,{\dot {\mathbf {Q} }},t),t),}$$ $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {Q}}_{i}}}={\frac {\partial L'}{\partial Q_{i}}}.}$$

Это может упростить уравнения движения.

Доказательство

Для преобразования координат имеем что подразумевает то что подразумевает то . ${\displaystyle Q_{i}=Q_{i}(\mathbf {q} ,t)}$ $${\displaystyle d{Q_{i}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}d{q_{k}}+{\frac {\partial Q_{k}}{\partial t}}dt,}$$ ${\displaystyle {\dot {Q_{i}}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial Q_{k}}{\partial t}}(\mathbf {q} ,t)}$ ${\displaystyle {\frac {\partial {\dot {Q_{i}}}}{\partial {\dot {q}}_{k}}}={\frac {\partial Q_{i}}{\partial q_{k}}}}$

Из этого также следует, что: и аналогично: откуда следует, что . Два полученных соотношения могут быть использованы в доказательстве. $${\displaystyle {\frac {\partial {\dot {Q_{i}}}}{\partial q_{j}}}=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{j}\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial q_{j}\partial t}}(\mathbf {q} ,t)}$$ $${\displaystyle {\frac {d}{dt}}\left({\frac {\partial {Q_{i}}}{\partial q_{j}}}\right)=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{k}\partial q_{j}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial t\partial q_{j}}}(\mathbf {q} ,t)}$$ ${\displaystyle {\frac {d}{dt}}\left({\frac {\partial Q_{i}}{\partial q_{k}}}\right)={\frac {\partial {\dot {Q}}_{i}}{\partial q_{k}}}}$

Исходя из уравнений Эйлера-Лагранжа в исходном наборе обобщенных координат, имеем: $${\displaystyle {\begin{aligned}{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {{\partial }L}{\partial q_{i}}}=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}\right)-{\frac {{\partial }L}{\partial Q_{k}}}{\frac {\partial Q_{k}}{\partial {q}_{i}}}-{\frac {{\partial }L}{\partial {\dot {Q}}_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {q}_{i}}}\right)=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right){\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}+{\frac {\partial L}{\partial {\dot {Q}}_{k}}}{\frac {d}{dt}}\left({\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}\right)-{\frac {{\partial }L}{\partial Q_{k}}}{\frac {\partial {\dot {Q}}_{k}}{\partial {\dot {q}}_{i}}}-{\frac {{\partial }L}{\partial {\dot {Q}}_{k}}}{\frac {d}{dt}}\left({\frac {\partial Q_{k}}{\partial q_{i}}}\right)\right)=0\\\sum _{k}\left({\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right)-{\frac {\partial L}{\partial {\dot {Q}}_{k}}}\right){\frac {\partial Q_{k}}{\partial q_{i}}}=0\\\end{aligned}}}$$

Поскольку преобразование из обратимо, то отсюда следует, что форма уравнения Эйлера-Лагранжа инвариантна, т.е. ${\displaystyle q\rightarrow Q}$ $${\displaystyle {\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {Q}}_{i}}}-{\frac {{\partial }L}{\partial Q_{i}}}=0.}$$

Циклические координаты и сохраняющиеся импульсы

Важным свойством лагранжиана является то, что сохраняющиеся величины могут быть легко считаны из него. Обобщенный импульс, «канонически сопряженный» с координатой q _i, определяется как $${\displaystyle p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}}.}$$

Если лагранжиан L не зависит от некоторой координаты q _i , то из уравнений Эйлера–Лагранжа немедленно следует, что и интегрирование показывает, что соответствующий обобщенный импульс равен константе, сохраняющейся величине. Это частный случай теоремы Нётер . Такие координаты называются «циклическими» или «игнорируемыми». $${\displaystyle {\dot {p}}_{i}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}={\frac {\partial L}{\partial q_{i}}}=0}$$

Например, система может иметь лагранжиан , где r и z — длины вдоль прямых линий, s — длина дуги вдоль некоторой кривой, а θ и φ — углы. Обратите внимание, что z , s и φ отсутствуют в лагранжиане, хотя их скорости отсутствуют. Тогда все импульсы являются сохраняющимися величинами. Единицы и природа каждого обобщенного импульса будут зависеть от соответствующей координаты; в этом случае p _z — это поступательный импульс в направлении z , p _s — это также поступательный импульс вдоль кривой, в которой измеряется s , а p _φ — это угловой момент в плоскости, в которой измеряется угол φ . Каким бы сложным ни было движение системы, все координаты и скорости будут изменяться таким образом, что эти импульсы будут сохраняться. $${\displaystyle L(r,\theta ,{\dot {s}},{\dot {z}},{\dot {r}},{\dot {\theta }},{\dot {\phi }},t),}$$ $${\displaystyle p_{z}={\frac {\partial L}{\partial {\dot {z}}}},\quad p_{s}={\frac {\partial L}{\partial {\dot {s}}}},\quad p_{\phi }={\frac {\partial L}{\partial {\dot {\phi }}}},}$$

Энергия

При наличии лагранжиана гамильтониан соответствующей механической системы по определению равен Эта величина будет эквивалентна энергии, если обобщенные координаты являются естественными координатами, т. е. они не имеют явной зависимости от времени при выражении вектора положения: . Откуда: где — симметричная матрица, которая определяется для вывода. ${\displaystyle L,}$ $${\displaystyle H={\biggl (}\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}{\biggr )}-L.}$$ ${\displaystyle \mathbf {r} =\mathbf {r} (q_{1},\cdots ,q_{n})}$ $${\displaystyle T={\frac {m}{2}}v^{2}={\frac {m}{2}}\sum _{i,j}\left({\frac {\partial {\vec {r}}}{\partial q_{i}}}{\dot {q}}_{i}\right)\cdot \left({\frac {\partial {\vec {r}}}{\partial q_{j}}}{\dot {q}}_{j}\right)={\frac {m}{2}}\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}}$$ $${\displaystyle \sum _{k=1}^{n}{\dot {q}}_{k}{\frac {\partial L}{\partial {\dot {q}}_{k}}}=\sum _{k=1}^{n}{\dot {q}}_{k}{\frac {\partial T}{\partial {\dot {q}}_{k}}}={\frac {m}{2}}\left(2\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}\right)=2T}$$ $${\displaystyle H=\left(\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)-L=2T-(T-V)=T+V=E}$$ ${\displaystyle a_{ij}={\frac {\partial \mathbf {r} }{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} }{\partial q_{j}}}}$

Инвариантность относительно преобразований координат

В каждый момент времени t энергия инвариантна относительно изменения координат конфигурационного пространства q → Q , т.е. (используя естественные координаты) Помимо этого результата, приведенное ниже доказательство показывает, что при таком изменении координат производные изменяются как коэффициенты линейной формы. $${\displaystyle E(\mathbf {q} ,{\dot {\mathbf {q} }},t)=E(\mathbf {Q} ,{\dot {\mathbf {Q} }},t).}$$ ${\displaystyle \partial L/\partial {\dot {q}}_{i}}$

Доказательство

Для преобразования координат Q = F ( q ) имеем , где — касательное отображение векторного пространства в векторное пространство , а — якобиан. В координатах и ​​предыдущая формула для имеет вид После дифференцирования с использованием правила произведения, где $${\displaystyle d\mathbf {Q} =F_{*}(\mathbf {q} )d\mathbf {q} ,}$$ ${\displaystyle F_{*}(\mathbf {q} )}$ $${\displaystyle \left\{\sum _{i=1}^{n}{\dot {q}}_{i}\cdot \left(\left.{\frac {\partial }{\partial q_{i}}}\right|_{\mathbf {q} }\right)\ {\biggl |}\ {\dot {q}}_{i}\in \mathbb {R} \right\}}$$ $${\displaystyle \left\{\sum _{i=1}^{n}{\dot {Q}}_{i}\cdot \left(\left.{\frac {\partial }{\partial Q_{i}}}\right|_{F(\mathbf {q} )}\right)\ {\biggl |}\ {\dot {Q}}_{i}\in \mathbb {R} \right\},}$$ $${\displaystyle \textstyle F_{*}(\mathbf {q} )=\left(\left.{\frac {\partial F_{i}}{\partial q_{j}}}\right|_{\mathbf {q} }\right)_{i,j=1}^{n}}$$ ${\displaystyle {\dot {q}}_{i}}$ ${\displaystyle {\dot {Q}}_{i},}$ ${\displaystyle d\mathbf {Q} }$ ${\displaystyle {\dot {\mathbf {Q} }}=F_{*}(\mathbf {q} ){\dot {\mathbf {q} }}.}$ $${\displaystyle d{\dot {\mathbf {Q} }}=G(\mathbf {q} ,{\dot {\mathbf {q} }})d\mathbf {q} +F_{*}(\mathbf {q} )d{\dot {\mathbf {q} }},}$$ $${\displaystyle {\begin{aligned}G(\mathbf {q} ,{\dot {\mathbf {q} }})d\mathbf {q} &\,{\stackrel {\text{def}}{=}}\,d(F_{*}(\mathbf {q} )){\dot {\mathbf {q} }}=\left(\sum _{k=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }dq_{k}\right)_{i,j=1}^{n}{\dot {\mathbf {q} }}=\left(\sum _{j=1}^{n}{\dot {q}}_{j}\sum _{k=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }dq_{k}\right)_{i=1,\ldots ,n}^{T}\\&=\left(\sum _{k=1}^{n}dq_{k}\sum _{j=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }{\dot {q}}_{j}\right)_{i=1,\ldots ,n}^{T}=\left(\sum _{j=1}^{n}{\frac {\partial ^{2}F_{i}}{\partial q_{j}\partial q_{k}}}{\biggl |}_{\mathbf {q} }{\dot {q}}_{j}\right)_{i,k=1}^{n}d\mathbf {q} .\end{aligned}}}$$

В векторной записи, $${\displaystyle {\begin{aligned}dL(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)&={\frac {\partial L}{\partial \mathbf {Q} }}d\mathbf {Q} +{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}d{\dot {\mathbf {Q} }}+{\frac {\partial L}{\partial t}}dt\\&=\left({\frac {\partial L}{\partial \mathbf {Q} }}F_{*}(\mathbf {q} )+{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}G(\mathbf {q} ,{\dot {\mathbf {q} }})\right)d\mathbf {q} +{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}F_{*}(\mathbf {q} )d{\dot {\mathbf {q} }}+{\frac {\partial L}{\partial t}}.\end{aligned}}}$$

С другой стороны, $${\displaystyle dL(\mathbf {q} ,{\dot {\mathbf {q} }},t)={\frac {\partial L}{\partial \mathbf {q} }}d\mathbf {q} +{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}d{\dot {\mathbf {q} }}+{\frac {\partial L}{\partial t}}dt.}$$

Ранее упоминалось, что лагранжианы не зависят от выбора координат конфигурационного пространства, т. е. Одним из следствий этого является то, что и Это показывает, что для каждого и есть хорошо определенная линейная форма, коэффициенты которой являются контравариантными 1-тензорами. Применение обеих сторон уравнения к и использование приведенной выше формулы для дает Инвариантность энергии следует. ${\displaystyle L(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=L(\mathbf {q} ,{\dot {\mathbf {q} }},t).}$ ${\displaystyle dL(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=dL(\mathbf {q} ,{\dot {\mathbf {q} }},t),}$ $${\displaystyle {\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}F_{*}(\mathbf {q} )={\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}.}$$ ${\displaystyle \mathbf {q} ,}$ ${\displaystyle {\dot {\mathbf {q} }},}$ ${\displaystyle t,}$ ${\displaystyle \textstyle \sum \limits _{i=1}^{n}{\frac {\partial L}{\partial {\dot {q}}_{i}}}d{\dot {q}}_{i}}$ ${\displaystyle \textstyle {\frac {\partial L}{\partial {\dot {q}}_{i}}}}$ ${\displaystyle {\dot {\mathbf {q} }}}$ ${\displaystyle {\dot {\mathbf {Q} }}}$ $${\displaystyle {\dot {\mathbf {Q} }}{\frac {\partial L}{\partial {\dot {\mathbf {Q} }}}}={\dot {\mathbf {q} }}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}.}$$ ${\displaystyle E}$

Сохранение

В механике Лагранжа система замкнута тогда и только тогда, когда ее лагранжиан явно не зависит от времени. Закон сохранения энергии гласит, что энергия замкнутой системы является интегралом движения . ${\displaystyle L}$ ${\displaystyle E}$

Точнее, пусть q = q ( t ) будет экстремалью . (Другими словами, q удовлетворяет уравнениям Эйлера–Лагранжа). Взятие полной производной по времени от L вдоль этой экстремали и использование уравнений EL приводит к $${\displaystyle {\begin{aligned}{\frac {dL}{dt}}&={\dot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}+{\frac {\partial L}{\partial t}}\\-{\frac {\partial L}{\partial t}}&={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\right){\dot {\mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}-{\dot {L}}\\-{\frac {\partial L}{\partial t}}&={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\mathbf {\dot {q}} -L\right)={\frac {dH}{dt}}\end{aligned}}}$$

Если лагранжиан L явно не зависит от времени, то ∂ L /∂ t = 0 , тогда H не меняется со временем эволюции частицы, фактически являясь интегралом движения, что означает, что Следовательно, если выбранные координаты являются естественными координатами, энергия сохраняется. $${\displaystyle H(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)={\text{constant of time}}.}$$

Кинетическая и потенциальная энергия

При всех этих обстоятельствах ^[42] константа — это полная энергия системы. Кинетическая и потенциальная энергии все еще изменяются по мере развития системы, но движение системы будет таким, что их сумма, полная энергия, будет постоянной. Это ценное упрощение, поскольку энергия E — это константа интегрирования, которая считается произвольной константой для задачи, и может быть возможным интегрировать скорости из этого энергетического соотношения для решения для координат. $${\displaystyle E=T+V}$$

Механическое сходство

Если потенциальная энергия является однородной функцией координат и не зависит от времени, ^[43] и все векторы положения масштабируются одной и той же ненулевой константой α , r _k ′ = α r _k , так что и время масштабируется множителем β , t ′ = βt , то скорости v _k масштабируются множителем α / β , а кинетическая энергия T - множителем ( α / β ) ² . Весь лагранжиан масштабируется тем же множителем, если $${\displaystyle V(\alpha \mathbf {r} _{1},\alpha \mathbf {r} _{2},\ldots ,\alpha \mathbf {r} _{N})=\alpha ^{N}V(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N})}$$ $${\displaystyle {\frac {\alpha ^{2}}{\beta ^{2}}}=\alpha ^{N}\quad \Rightarrow \quad \beta =\alpha ^{1-{\frac {N}{2}}}.}$$

Поскольку длины и времена были масштабированы, траектории частиц в системе следуют геометрически подобным путям, отличающимся по размеру. Длина l, пройденная за время t в исходной траектории, соответствует новой длине l ′, пройденной за время t ′ в новой траектории, заданной соотношениями $${\displaystyle {\frac {t'}{t}}=\left({\frac {l'}{l}}\right)^{1-{\frac {N}{2}}}.}$$

Взаимодействующие частицы

Для данной системы, если две подсистемы A и B не взаимодействуют, лагранжиан L всей системы представляет собой сумму лагранжианов L _A и L _B для подсистем: ^[38] $${\displaystyle L=L_{A}+L_{B}.}$$

Если они взаимодействуют, то это невозможно. В некоторых ситуациях может оказаться возможным разделить лагранжиан системы L на сумму невзаимодействующих лагранжианов, плюс еще один лагранжиан L _AB, содержащий информацию о взаимодействии, $${\displaystyle L=L_{A}+L_{B}+L_{AB}.}$$

Это может быть физически мотивировано, если принять невзаимодействующие лагранжианы только за кинетические энергии, в то время как лагранжиан взаимодействия является полной потенциальной энергией системы. Кроме того, в предельном случае пренебрежимо малого взаимодействия L _AB стремится к нулю, что сводится к невзаимодействующему случаю выше.

Расширение на более чем две невзаимодействующие подсистемы простое – общий лагранжиан является суммой отдельных лагранжианов для каждой подсистемы. Если есть взаимодействия, то могут быть добавлены лагранжианы взаимодействия.

Следствия сингулярных лагранжианов

Из уравнений Эйлера-Лагранжа следует, что: $${\displaystyle {\begin{aligned}&{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {\partial L}{\partial q_{i}}}=0\\&{\frac {\partial ^{2}L}{\partial q_{j}\partial {\dot {q}}_{i}}}{\frac {dq_{j}}{dt}}+{\frac {\partial ^{2}L}{\partial {\dot {q}}_{j}\partial {\dot {q}}_{i}}}{\frac {d{\dot {q}}_{j}}{dt}}+{\frac {\partial L}{\partial t}}-{\frac {\partial L}{\partial q_{i}}}=0\\&\sum _{j}W_{ij}(q,{\dot {q}},t){\ddot {q}}_{j}={\frac {\partial L}{\partial q_{i}}}-{\frac {\partial L}{\partial t}}-\sum _{j}{\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial q_{j}}}{\dot {q}}_{j},\\\end{aligned}}}$$

где матрица определяется как . Если матрица невырожденная, приведенные выше уравнения можно решить, чтобы представить как функцию от . Если матрица необратимая, то невозможно будет представить все как функцию от , но также гамильтоновы уравнения движения не примут стандартную форму. ^[44] ${\displaystyle W_{ij}={\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}}$ ${\displaystyle W}$ ${\displaystyle {\ddot {q}}}$ ${\displaystyle ({\dot {q}},q,t)}$ ${\displaystyle {\ddot {q}}}$ ${\displaystyle ({\dot {q}},q,t)}$

Примеры

В следующих примерах показано применение уравнений Лагранжа второго рода к механическим задачам.

Консервативная сила

Частица массой m движется под действием консервативной силы, полученной из градиента ∇ скалярного потенциала , $${\displaystyle \mathbf {F} =-{\boldsymbol {\nabla }}V(\mathbf {r} ).}$$

Если частиц больше, то в соответствии с приведенными выше результатами полная кинетическая энергия представляет собой сумму всех кинетических энергий частиц, а потенциал является функцией всех координат.

Декартовы координаты

Лагранжиан частицы можно записать $${\displaystyle L(x,y,z,{\dot {x}},{\dot {y}},{\dot {z}})={\frac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})-V(x,y,z).}$$

Уравнения движения частицы находятся путем применения уравнения Эйлера–Лагранжа для координаты x с производными отсюда и аналогично для координат y и z . Собирая уравнения в векторной форме, находим, что является вторым законом движения Ньютона для частицы, подверженной действию консервативной силы. $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)={\frac {\partial L}{\partial x}},}$$ $${\displaystyle {\frac {\partial L}{\partial x}}=-{\frac {\partial V}{\partial x}},\quad {\frac {\partial L}{\partial {\dot {x}}}}=m{\dot {x}},\quad {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)=m{\ddot {x}},}$$ $${\displaystyle m{\ddot {x}}=-{\frac {\partial V}{\partial x}},}$$ $${\displaystyle m{\ddot {\mathbf {r} }}=-{\boldsymbol {\nabla }}V}$$

Полярные координаты в 2D и 3D

Используя сферические координаты ( r , θ , φ ) , обычно используемые в физике (конвенция ISO 80000-2:2019), где r — радиальное расстояние до начала координат, θ — полярный угол (также известный как коширота, зенитный угол, нормальный угол или угол наклона), а φ — азимутальный угол, лагранжиан для центрального потенциала имеет вид Таким образом, в сферических координатах уравнения Эйлера — Лагранжа имеют вид Координата φ является циклической, поскольку она не появляется в лагранжиане, поэтому сохраняющийся импульс в системе представляет собой угловой момент, в котором r , θ и dφ / dt могут изменяться со временем, но только таким образом, что p _φ является постоянным. $${\displaystyle L={\frac {m}{2}}({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}\sin ^{2}\theta \,{\dot {\varphi }}^{2})-V(r).}$$ $${\displaystyle m{\ddot {r}}-mr({\dot {\theta }}^{2}+\sin ^{2}\theta \,{\dot {\varphi }}^{2})+{\frac {\partial V}{\partial r}}=0,}$$ $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}{\dot {\theta }})-mr^{2}\sin \theta \cos \theta \,{\dot {\varphi }}^{2}=0,}$$ $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}\sin ^{2}\theta \,{\dot {\varphi }})=0.}$$ $${\displaystyle p_{\varphi }={\frac {\partial L}{\partial {\dot {\varphi }}}}=mr^{2}\sin ^{2}\theta {\dot {\varphi }},}$$

Лагранжиан в двумерных полярных координатах восстанавливается путем фиксации θ на постоянном значении π /2.

Маятник на подвижной опоре

Эскиз ситуации с определением координат (кликните для увеличения)

Рассмотрим маятник массой m и длиной ℓ , прикрепленный к опоре массой M , которая может перемещаться вдоль линии в направлении . Пусть будет координатой вдоль линии опоры, и обозначим положение маятника углом к ​​вертикали. Координаты и компоненты скорости груза маятника равны ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle \theta }$ $${\displaystyle {\begin{array}{rll}&x_{\mathrm {pend} }=x+\ell \sin \theta &\quad \Rightarrow \quad {\dot {x}}_{\mathrm {pend} }={\dot {x}}+\ell {\dot {\theta }}\cos \theta \\&y_{\mathrm {pend} }=-\ell \cos \theta &\quad \Rightarrow \quad {\dot {y}}_{\mathrm {pend} }=\ell {\dot {\theta }}\sin \theta .\end{array}}}$$

Обобщенные координаты можно принять равными и . Кинетическая энергия системы тогда равна , а потенциальная энергия дает лагранжиан ${\displaystyle x}$ ${\displaystyle \theta }$ $${\displaystyle T={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left({\dot {x}}_{\mathrm {pend} }^{2}+{\dot {y}}_{\mathrm {pend} }^{2}\right)}$$ $${\displaystyle V=mgy_{\mathrm {pend} }}$$ $${\displaystyle {\begin{array}{rcl}L&=&T-V\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&=&{\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}+mg\ell \cos \theta .\end{array}}}$$

Поскольку x отсутствует в лагранжиане, это циклическая координата. Сохраняющийся импульс равен и уравнение Лагранжа для опорной координаты равно $${\displaystyle p_{x}={\frac {\partial L}{\partial {\dot {x}}}}=(M+m){\dot {x}}+m\ell {\dot {\theta }}\cos \theta ,}$$ ${\displaystyle x}$ $${\displaystyle (M+m){\ddot {x}}+m\ell {\ddot {\theta }}\cos \theta -m\ell {\dot {\theta }}^{2}\sin \theta =0.}$$

Уравнение Лагранжа для угла θ имеет вид и упрощается $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left[m({\dot {x}}\ell \cos \theta +\ell ^{2}{\dot {\theta }})\right]+m\ell ({\dot {x}}{\dot {\theta }}+g)\sin \theta =0;}$$ $${\displaystyle {\ddot {\theta }}+{\frac {\ddot {x}}{\ell }}\cos \theta +{\frac {g}{\ell }}\sin \theta =0.}$$

Эти уравнения могут выглядеть довольно сложными, но их нахождение с помощью законов Ньютона потребовало бы тщательного определения всех сил, что было бы гораздо более трудоемким и подверженным ошибкам. Рассматривая предельные случаи, можно проверить правильность этой системы: например, should дает уравнения движения для простого маятника , который находится в состоянии покоя в некоторой инерциальной системе отсчета , в то время как should дает уравнения для маятника в постоянно ускоряющейся системе и т. д. Более того, тривиально получить результаты численно, задав подходящие начальные условия и выбранный временной шаг, проходя по результатам итеративно . ${\displaystyle {\ddot {x}}\to 0}$ ${\displaystyle {\ddot {\theta }}\to 0}$

Задача двух тел с центральной силой

Два тела массами m ₁ и m ₂ с радиус-векторами r ₁ и r ₂ находятся на орбите друг вокруг друга из-за притягивающего центрального потенциала V . Мы можем записать лагранжиан в терминах координат положения, как они есть, но это установленная процедура для преобразования задачи двух тел в задачу одного тела следующим образом. Введем координаты Якоби ; разделение тел r = r ₂ − r ₁ и местоположение центра масс R = ( m ₁ r ₁ + m ₂ r ₂ )/( m ₁ + m ₂ ) . Тогда лагранжиан будет ^{[45] [46] [nb 4]} где M = m ₁ + m ₂ - полная масса, μ = m ₁ m ₂ /( m ₁ + m ₂ ) - приведенная масса , а V - потенциал радиальной силы, который зависит только от величины разделения | r | = | r ₂ − r ₁ | . Лагранжиан распадается на член центра масс L _cm и член относительного движения L _rel . $${\displaystyle L=\underbrace {{\frac {1}{2}}M{\dot {\mathbf {R} }}^{2}} _{L_{\text{cm}}}+\underbrace {{\frac {1}{2}}\mu {\dot {\mathbf {r} }}^{2}-V(|\mathbf {r} |)} _{L_{\text{rel}}}}$$

Уравнение Эйлера–Лагранжа для R — это простое утверждение, что центр масс движется по прямой с постоянной скоростью. $${\displaystyle M{\ddot {\mathbf {R} }}=0,}$$

Поскольку относительное движение зависит только от величины разделения, идеальным решением будет использовать полярные координаты ( r , θ ) и взять r = | r | , так что θ — это циклическая координата с соответствующим сохраняющимся (угловым) импульсом $${\displaystyle L_{\text{rel}}={\frac {1}{2}}\mu \left({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\right)-V(r),}$$ $${\displaystyle p_{\theta }={\frac {\partial L_{\text{rel}}}{\partial {\dot {\theta }}}}=\mu r^{2}{\dot {\theta }}=\ell .}$$

Радиальная координата r и угловая скорость d θ /d t могут изменяться со временем, но только таким образом, что ℓ постоянна. Уравнение Лагранжа для r имеет вид $${\displaystyle \mu r{\dot {\theta }}^{2}-{\frac {dV}{dr}}=\mu {\ddot {r}}.}$$

Это уравнение идентично радиальному уравнению, полученному с использованием законов Ньютона в совместно вращающейся системе отсчета, то есть системе, вращающейся с приведенной массой, так что она кажется неподвижной. Исключая угловую скорость d θ /d t из этого радиального уравнения, ^[47] которое является уравнением движения для одномерной задачи, в которой частица массы μ подвергается воздействию внутренней центральной силы −d V /d r и второй внешней силы, называемой в этом контексте (лагранжевой) центробежной силой (см. центробежная сила#Другие применения термина ): $${\displaystyle \mu {\ddot {r}}=-{\frac {\mathrm {d} V}{\mathrm {d} r}}+{\frac {\ell ^{2}}{\mu r^{3}}}.}$$ $${\displaystyle F_{\mathrm {cf} }=\mu r{\dot {\theta }}^{2}={\frac {\ell ^{2}}{\mu r^{3}}}.}$$

Конечно, если полностью оставаться в рамках одномерной формулировки, то ℓ входит только как некоторый навязанный параметр внешней силы, направленной наружу, и его интерпретация как момента импульса зависит от более общей двумерной задачи, из которой возникла одномерная задача.

Если прийти к этому уравнению, используя ньютоновскую механику в совместно вращающейся системе отсчета, то интерпретация очевидна как центробежная сила в этой системе отсчета из-за вращения самой системы отсчета. Если прийти к этому уравнению напрямую, используя обобщенные координаты ( r , θ ) и просто следуя формулировке Лагранжа, вообще не думая о системах отсчета, то интерпретация будет такова, что центробежная сила является результатом использования полярных координат . Как говорит Хильдебранд: ^[48]

«Поскольку такие величины не являются истинными физическими силами, их часто называют силами инерции . Их наличие или отсутствие зависит не от конкретной рассматриваемой задачи, а от выбранной системы координат ». В частности, если выбраны декартовы координаты, то центробежная сила исчезает, и формула включает только саму центральную силу, которая обеспечивает центростремительную силу для криволинейного движения.

Эта точка зрения, что фиктивные силы возникают из-за выбора координат, часто выражается пользователями метода Лагранжа. Эта точка зрения возникает естественным образом в подходе Лагранжа, поскольку система отсчета (возможно, неосознанно) выбирается выбором координат. Например, см. ^[49] для сравнения лагранжианов в инерциальной и неинерциальной системах отсчета. См. также обсуждение «полных» и «обновленных» формулировок Лагранжа в ^[50] К сожалению, такое использование «инерционной силы» противоречит ньютоновской идее инерционной силы. С точки зрения Ньютона, инерционная сила возникает из-за ускорения системы наблюдения (того факта, что она не является инерциальной системой отсчета ), а не из-за выбора системы координат. Чтобы сохранить ясность, безопаснее всего называть лагранжевы инерционные силы обобщенными инерционными силами, чтобы отличать их от ньютоновских векторных инерционных сил. То есть следует избегать следования Хильдебранду, когда он говорит (стр. 155): «Мы всегда имеем дело с обобщенными силами, скоростями, ускорениями и импульсами. Для краткости прилагательное «обобщенный» будет часто опускаться».

Известно, что лагранжиан системы не является единственным. В рамках лагранжева формализма фиктивные силы Ньютона могут быть идентифицированы по существованию альтернативных лагранжианов, в которых фиктивные силы исчезают, иногда найденных путем использования симметрии системы. ^[51]

Расширения для включения неконсервативных сил

Диссипативные силы

Диссипацию (т.е. неконсервативные системы) можно также рассматривать с помощью эффективного лагранжиана, сформулированного с помощью определенного удвоения степеней свободы. ^{[52] [53] [54] [55]}

В более общей формулировке силы могут быть как консервативными, так и вязкими . Если из F _i можно найти соответствующее преобразование , Рэлей предлагает использовать функцию диссипации , D , следующего вида: ^[56] где C _jk — константы, которые связаны с коэффициентами затухания в физической системе, хотя и не обязательно равны им. Если D определяется таким образом, то ^[56] и $${\displaystyle D={\frac {1}{2}}\sum _{j=1}^{m}\sum _{k=1}^{m}C_{jk}{\dot {q}}_{j}{\dot {q}}_{k},}$$ $${\displaystyle Q_{j}=-{\frac {\partial V}{\partial q_{j}}}-{\frac {\partial D}{\partial {\dot {q}}_{j}}}}$$ $${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial L}{\partial q_{j}}}+{\frac {\partial D}{\partial {\dot {q}}_{j}}}=0.}$$

Электромагнетизм

Тестовая частица — это частица, масса и заряд которой считаются настолько малыми, что ее влияние на внешнюю систему незначительно. Часто это гипотетическая упрощенная точечная частица без свойств, кроме массы и заряда. Реальные частицы, такие как электроны и верхние кварки , более сложны и имеют дополнительные члены в своих лагранжианах. Поля не только могут образовывать неконсервативные потенциалы, эти потенциалы также могут зависеть от скорости.

Лагранжиан для заряженной частицы с электрическим зарядом q , взаимодействующей с электромагнитным полем , является прототипическим примером потенциала, зависящего от скорости. Электрический скалярный потенциал ϕ = ϕ ( r , t ) и магнитный векторный потенциал A = A ( r , t ) определяются из электрического поля E = E ( r , t ) и магнитного поля B = B ( r , t ) следующим образом: $${\displaystyle \mathbf {E} =-{\boldsymbol {\nabla }}\phi -{\frac {\partial \mathbf {A} }{\partial t}},\quad \mathbf {B} ={\boldsymbol {\nabla }}\times \mathbf {A} .}$$

Лагранжиан массивной заряженной пробной частицы в электромагнитном поле называется минимальной связью . Это хороший пример того, когда общее правило , что лагранжиан равен кинетической энергии за вычетом потенциальной энергии, неверно. В сочетании с уравнением Эйлера-Лагранжа это дает закон силы Лоренца $${\displaystyle L={\tfrac {1}{2}}m{\dot {\mathbf {r} }}^{2}+q\,{\dot {\mathbf {r} }}\cdot \mathbf {A} -q\phi ,}$$ $${\displaystyle m{\ddot {\mathbf {r} }}=q\mathbf {E} +q{\dot {\mathbf {r} }}\times \mathbf {B} }$$

При калибровочном преобразовании : где f ( r , t ) — любая скалярная функция пространства и времени, вышеупомянутый лагранжиан преобразуется следующим образом: что по-прежнему дает тот же закон силы Лоренца. $${\displaystyle \mathbf {A} \rightarrow \mathbf {A} +{\boldsymbol {\nabla }}f,\quad \phi \rightarrow \phi -{\dot {f}},}$$ $${\displaystyle L\rightarrow L+q\left({\dot {\mathbf {r} }}\cdot {\boldsymbol {\nabla }}+{\frac {\partial }{\partial t}}\right)f=L+q{\frac {df}{dt}},}$$

Обратите внимание, что канонический импульс (сопряженный с положением r ) представляет собой кинетический импульс плюс вклад поля A (известный как потенциальный импульс): $${\displaystyle \mathbf {p} ={\frac {\partial L}{\partial {\dot {\mathbf {r} }}}}=m{\dot {\mathbf {r} }}+q\mathbf {A} .}$$

Это соотношение также используется в минимальном предписании связи в квантовой механике и квантовой теории поля . Из этого выражения мы можем видеть, что канонический импульс p не является калибровочно-инвариантным и, следовательно, не является измеримой физической величиной; Однако, если r является циклическим (т.е. лагранжиан не зависит от положения r ), что происходит, если поля ϕ и A однородны, то этот канонический импульс p, заданный здесь, является сохраняющимся импульсом, в то время как измеримый физический кинетический импульс m v не является.

Другие контексты и формулировки

Идеи механики Лагранжа имеют многочисленные приложения в других областях физики и могут использовать обобщенные результаты вариационного исчисления.

Альтернативные формулировки классической механики

Тесно связанной формулировкой классической механики является гамильтонова механика . Гамильтониан определяется и может быть получен путем выполнения преобразования Лежандра над лагранжианом, которое вводит новые переменные, канонически сопряженные с исходными переменными. Например, если задан набор обобщенных координат, канонически сопряженными переменными являются обобщенные импульсы. Это удваивает число переменных, но делает дифференциальные уравнения первым порядком. Гамильтониан является особенно вездесущей величиной в квантовой механике (см. Гамильтониан (квантовая механика) ). $${\displaystyle H=\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-L}$$

Механика Рауса представляет собой гибридную формулировку механики Лагранжа и Гамильтона, которая нечасто используется на практике, но является эффективной формулировкой для циклических координат.

Формулировка импульсного пространства

Уравнения Эйлера–Лагранжа также можно сформулировать в терминах обобщенных импульсов, а не обобщенных координат. Выполнение преобразования Лежандра над обобщенным координатным лагранжианом L ( q , d q /d t , t ) дает обобщенный импульсный лагранжиан L ′( p , d p /d t , t ) в терминах исходного лагранжиана, а также уравнения ЭЛ в терминах обобщенных импульсов. Оба лагранжиана содержат одну и ту же информацию, и любой из них может быть использован для решения задачи о движении системы. На практике обобщенные координаты удобнее использовать и интерпретировать, чем обобщенные импульсы.

Высшие производные обобщенных координат

Нет никаких математических причин ограничивать производные обобщенных координат только первым порядком. Можно вывести модифицированные уравнения ЭЛ для лагранжиана, содержащего производные более высокого порядка, см. подробности в уравнении Эйлера–Лагранжа . Однако с физической точки зрения существует препятствие для включения производных по времени выше первого порядка, что подразумевается конструкцией Остроградского канонического формализма для невырожденных лагранжианов с более высокими производными, см. Неустойчивость Остроградского

Оптика

Механику Лагранжа можно применить к геометрической оптике , применив вариационные принципы к лучам света в среде, а решение уравнений ЭЛ дает уравнения траекторий, по которым следуют световые лучи.

Релятивистская формулировка

Лагранжеву механику можно сформулировать в специальной теории относительности и общей теории относительности . Некоторые черты лагранжевой механики сохраняются в релятивистских теориях, но в других отношениях быстро возникают трудности. В частности, уравнения ЭЛ принимают ту же форму, и связь между циклическими координатами и сохраняющимися импульсами по-прежнему применима, однако лагранжиан должен быть модифицирован и не является просто кинетической энергией частицы минус потенциальная. Кроме того, не так просто обрабатывать многочастичные системы явно ковариантным способом, это может быть возможно, если выделить определенную систему отсчета.

Квантовая механика

В квантовой механике действие и квантово-механическая фаза связаны через постоянную Планка , а принцип стационарного действия можно понять в терминах конструктивной интерференции волновых функций .

В 1948 году Фейнман открыл формулировку интеграла по траектории, расширяющую принцип наименьшего действия на квантовую механику для электронов и фотонов . В этой формулировке частицы проходят все возможные пути между начальным и конечным состояниями; вероятность определенного конечного состояния получается путем суммирования по всем возможным траекториям, ведущим к нему. В классическом режиме формулировка интеграла по траектории чисто воспроизводит принцип Гамильтона и принцип Ферма в оптике .

Классическая теория поля

В механике Лагранжа обобщенные координаты образуют дискретный набор переменных, которые определяют конфигурацию системы. В классической теории поля физическая система не является набором дискретных частиц, а скорее непрерывным полем ϕ ( r , t ), определенным в области трехмерного пространства. С полем связана плотность Лагранжа , определяемая в терминах поля и его пространственных и временных производных в точке r и времени t . Аналогично случаю частиц, для нерелятивистских приложений плотность Лагранжа также является плотностью кинетической энергии поля за вычетом его плотности потенциальной энергии (это неверно в общем случае, и плотность Лагранжа должна быть «обратно спроектирована»). Тогда Лагранжиан является объемным интегралом плотности Лагранжа по трехмерному пространству , где d ³ r является трехмерным дифференциальным элементом объема . Лагранжиан является функцией времени, поскольку плотность лагранжиана имеет неявную пространственную зависимость через поля и может иметь явную пространственную зависимость, но они удаляются в интеграле, оставляя только время в качестве переменной для лагранжиана. $${\displaystyle {\mathcal {L}}(\phi ,\nabla \phi ,{\dot {\phi }},\mathbf {r} ,t)}$$ $${\displaystyle L(t)=\int {\mathcal {L}}\,\mathrm {d} ^{3}\mathbf {r} }$$

Теорема Нётер

Принцип действия и лагранжев формализм тесно связаны с теоремой Нётер , которая связывает сохраняющиеся физические величины с непрерывными симметриями физической системы.

Если лагранжиан инвариантен относительно симметрии, то результирующие уравнения движения также инвариантны относительно этой симметрии. Эта характеристика очень полезна для демонстрации того, что теории согласуются либо со специальной теорией относительности , либо с общей теорией относительности .

Смотрите также

• Астрономический портал

• Канонические координаты
• Основная лемма вариационного исчисления
• Функциональная производная
• Обобщенные координаты
• Гамильтонова механика
• Гамильтонова оптика
• Обратная задача механики Лагранжа , общая тема нахождения функции Лагранжа для системы по уравнениям движения.
• Лагранжева и эйлерова спецификация поля течения
• точка Лагранжа
• Лагранжева система
• Неавтономная механика
• Проблема Плато
• Ограниченная задача трех тел

Сноски

1. Иногда в этом контексте используется вариационная производная , обозначаемая и определяемая как . В этой статье используются только частные и полные производные. $${\displaystyle {\frac {\delta }{\delta \mathbf {r} _{k}}}\equiv {\frac {\partial }{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial }{\partial {\dot {\mathbf {r} }}_{k}}}}$$
2. Здесь виртуальные смещения предполагаются обратимыми, однако для некоторых систем возможны необратимые виртуальные смещения, которые нарушают этот принцип, см. уравнение Удвадиа–Калабы .
3. Другими словами , для частицы k, подверженной силе ограничения, однако из-за уравнений ограничения на координаты r _k . $${\displaystyle \mathbf {C} _{k}\cdot \delta \mathbf {r} _{k}=0}$$ $${\displaystyle C_{k\,x}\delta x_{k}\neq 0,\quad C_{k\,y}\delta y_{k}\neq 0,\quad C_{k\,z}\delta z_{k}\neq 0}$$
4. Лагранжиан также может быть явно записан для вращающейся системы отсчета. См. Padmanabhan, 2000.

Примечания

1. Фрейзер, Крейг. «Ранние вклады Ж. Л. Лагранжа в принципы и методы механики». Архив истории точных наук, т. 28, № 3, 1983, стр. 197–241. JSTOR, http://www.jstor.org/stable/41133689. Доступ 3 ноября 2023 г.
2. Хэнд и Финч 1998, стр. 23
3. Хэнд и Финч 1998, стр. 18–20.
4. Хэнд и Финч 1998, стр. 46, 51.
5. Ball, Philip (2019-09-13). "Обучение энергии прежде сил". Физика . стр. 100. doi :10.1103/PhysRevPhysEducRes.15.020126 . Получено 2024-09-27 .
6. Tatum, JB "Механика Лагранжа" (PDF) . www.astro.uvic.ca . Получено 2024-09-27 .
7. Парсонс, Пол; Диксон, Гейл (2016). 50 идей, которые вам действительно нужно знать: наука . Лондон: Quercus . С. 4–7. ISBN 9781784296148.
8. Торби 1984, стр. 270
9. Торби 1984, стр. 269
10. Кремаскини, Клаудио; Тессаротто, Массимо (2015-06-30). «Синхронные лагранжевы вариационные принципы в общей теории относительности». The European Physical Journal Plus . 130 (6): 123. doi :10.1140/epjp/i2015-15123-4. ISSN  2190-5444.
11. Bersani AM, Caressa P. Лагранжевы описания диссипативных систем: обзор. Математика и механика твердых тел . 2021;26(6):785-803. Doi: 10.1177/1081286520971834
12. Хэнд и Финч 1998, стр. 36–40.
13. Пфайффер, Фридрих (2008), Пфайффер, Фридрих (ред.), «Системы ограничений», Mechanical System Dynamics , Берлин, Гейдельберг: Springer, стр. 85–186, doi :10.1007/978-3-540-79436-3_3, ISBN 978-3-540-79436-3, получено 2024-09-23
14. Хэнд и Финч 1998, стр. 60–61.
15. Хэнд и Финч 1998, стр. 19
16. Пенроуз 2007
17. Морин, Д. (2007). Глава 6: Метод Лагранжа. В Методе Лагранжа . https://scholar.harvard.edu/files/david-morin/files/cmchap6.pdf
18. Кей 1988, стр. 156
19. Synge & Schild 1949, с. 150–152
20. Фостер и Найтингейл 1995, стр. 89
21. Хэнд и Финч 1998, стр. 4
22. Гольдштейн 1980, стр. 16–18.
23. Хэнд и Финч 1998, стр. 15
24. Хэнд и Финч 1998, стр. 15
25. Феттер и Валецкая 1980, стр. 53
26. Киббл и Беркшир 2004, стр. 234
27. Феттер и Валецкая 1980, стр. 56
28. Хэнд и Финч 1998, стр. 17
29. Хэнд и Финч 1998, стр. 15–17.
30. Р. Пенроуз (2007). Дорога к реальности . Старинные книги. стр. 474. ISBN 978-0-679-77631-4.
31. Гольдштейн 1980, стр. 23
32. Киббл и Беркшир 2004, стр. 234–235
33. Хэнд и Финч 1998, стр. 51
34. Hanc, Jozef; Taylor, Edwin F.; Tuleja, Slavomir (2005-07-01). «Вариационная механика в одном и двух измерениях». American Journal of Physics . 73 (7): 603–610. Bibcode : 2005AmJPh..73..603H. doi : 10.1119/1.1848516. ISSN  0002-9505.
35. Hand & Finch 1998, стр. 44–45
36. Гольдштейн 1980
37. Феттер и Валецкая 1980, стр. 68–70
38. Ландау и Лифшиц 1976, стр. 4
39. Голдштейн, Пул и Сафко 2002, стр. 21
40. Ландау и Лифшиц 1976, стр. 4
41. Гольдштейн 1980, стр. 21
42. Ландау и Лифшиц 1976, стр. 14
43. Ландау и Лифшиц 1976, стр. 22
44. Роте, Хайнц Дж.; Роте, Клаус Д. (2010). Классическая и квантовая динамика гамильтоновых систем со связями. World Scientific Lecture Notes in Physics. Том 81. WORLD SCIENTIFIC. стр. 7. doi :10.1142/7689. ISBN 978-981-4299-64-0.
45. Тейлор 2005, стр. 297
46. Падманабхан 2000, стр. 48
47. Хэнд и Финч 1998, стр. 140–141.
48. Хильдебранд 1992, стр. 156
49. Зак, Збилут и Мейерс 1997, стр. 202.
50. Шабана 2008, стр. 118–119
51. Ганнон 2006, стр. 267
52. Косяков 2007
53. Галерея 2013
54. Бирнхольц, Хадар и Кол 2014
55. Бирнхольц, Хадар и Кол 2013
56. Torby 1984, стр. 271

Ссылки

• Лагранж, JL (1811). Аналитическая механика. Том. 1.
• Лагранж, JL (1815). Аналитическая механика. Том. 2.
• Пенроуз, Роджер (2007). Дорога к реальности . Старинные книги. ISBN 978-0-679-77631-4.
• Ландау, Л. Д .; Лифшиц, Э. М. (15 января 1976 г.). Механика (3-е изд.). Butterworth Heinemann. стр. 134. ISBN 9780750628969.
• Ландау, Лев ; Лифшиц, Евгений (1975). Классическая теория полей . Elsevier Ltd. ISBN 978-0-7506-2768-9.
• Hand, LN; Finch, JD (1998). Аналитическая механика (2-е изд.). Cambridge University Press. ISBN 9780521575720.
• Салетан, Э. Дж.; Хосе, Дж. В. (1998). Классическая динамика: современный подход. Cambridge University Press. ISBN 9780521636360.
• Kibble, TWB; Berkshire, FH (2004). Классическая механика (5-е изд.). Imperial College Press. стр. 236. ISBN 9781860944352.
• Голдштейн, Герберт (1980). Классическая механика (2-е изд.). Сан-Франциско, Калифорния: Addison Wesley. ISBN 0201029189.
• Голдштейн, Герберт ; Пул, Чарльз П. младший; Сафко, Джон Л. (2002). Классическая механика (3-е изд.). Сан-Франциско, Калифорния: Addison Wesley. ISBN 0-201-65702-3.
• Ланцош, Корнелиус (1986). "II §5 Вспомогательные условия: λ-метод Лагранжа". Вариационные принципы механики (Переиздание Университета Торонто 1970 г., 4-е изд.). Courier Dover. стр. 43. ISBN 0-486-65067-7.
• Феттер, АЛ; Валецка, ДЖД (1980). Теоретическая механика частиц и сплошных сред. Довер. С. 53–57. ISBN 978-0-486-43261-8.
• Принцип наименьшего действия , Р. Фейнман
• Дворжак, Р.; Фрайстеттер, Флориан (2005). "§ 3.2 Уравнения Лагранжа первого рода". Хаос и устойчивость в планетарных системах . Биркхойзер. стр. 24. ISBN 3-540-28208-4.
• Хакен, Х. (2006). Информация и самоорганизация (3-е изд.). Springer. стр. 61. ISBN 3-540-33021-6.
• Генри Зацкис (1960). "§1.4 Уравнения Лагранжа второго рода". В DH Menzel (ред.). Основные формулы физики . Т. 1 (2-е изд.). Courier Dover. стр. 160. ISBN 0-486-60595-7.
• Хильдебранд, Фрэнсис Бегно (1992). Методы прикладной математики (Переиздание Prentice-Hall 1965 2-е изд.). Courier Dover. стр. 156. ISBN 0-486-67002-3.
• Зак, Михаил; Збилут, Джозеф П.; Мейерс, Рональд Э. (1997). От нестабильности к интеллекту. Springer. стр. 202. ISBN 3-540-63055-4.
• Шабана, Ахмед А. (2008). Вычислительная механика сплошной среды. Cambridge University Press. С. 118–119. ISBN 978-0-521-88569-0.
• Тейлор, Джон Роберт (2005). Классическая механика. University Science Books. стр. 297. ISBN 1-891389-22-X.
• Падманабхан, Тану (2000). "§2.3.2 Движение во вращающейся системе отсчета". Теоретическая астрофизика: Астрофизические процессы (3-е изд.). Cambridge University Press. стр. 48. ISBN 0-521-56632-0.
• Доути, Ноэль А. (1990). Лагранжево взаимодействие . Addison-Wesley Publishers Ltd. ISBN 0-201-41625-5.
• Косяков, БП (2007). Введение в классическую теорию частиц и полей. Берлин, Германия: Springer. doi :10.1007/978-3-540-40934-2. ISBN 978-3-540-40933-5.
• Galley, Chad R. (2013). "Классическая механика неконсервативных систем". Physical Review Letters . 110 (17): 174301. arXiv : 1210.2745 . Bibcode :2013PhRvL.110q4301G. doi :10.1103/PhysRevLett.110.174301. PMID  23679733. S2CID  14591873.
• Бирнхольц, Офек; Хадар, Шахар; Кол, Барак (2014). «Радиационная реакция на уровне действия». International Journal of Modern Physics A . 29 (24): 1450132–1450190. arXiv : 1402.2610 . Bibcode :2014IJMPA..2950132B. doi :10.1142/S0217751X14501322. S2CID  118541484.
• Бирнхольц, Офек; Хадар, Шахар; Кол, Барак (2013). "Теория постньютоновского излучения и реакции". Physical Review D. 88 ( 10): 104037. arXiv : 1305.6930 . Bibcode : 2013PhRvD..88j4037B. doi : 10.1103/PhysRevD.88.104037. S2CID  119170985.
• Роджер Ф. Ганс (2013). Инженерная динамика: от лагранжиана к моделированию. Нью-Йорк: Springer. ISBN 978-1-4614-3929-5.
• Ганнон, Терри (2006). Лунный свет за пределами монстра: мост, соединяющий алгебру, модульные формы и физику. Cambridge University Press. стр. 267. ISBN 0-521-83531-3.
• Торби, Брюс (1984). «Энергетические методы». Продвинутая динамика для инженеров . Серия HRW по машиностроению. Соединенные Штаты Америки: CBS College Publishing. ISBN 0-03-063366-4.
• Фостер, Дж.; Найтингейл, Дж.Д. (1995). Краткий курс общей теории относительности (2-е изд.). Springer. ISBN 0-03-063366-4.
• MP Hobson; GP Efstathiou; AN Lasenby (2006). Общая теория относительности: Введение для физиков. Cambridge University Press. С. 79–80. ISBN 9780521829519.
• Синг, Дж. Л.; Шильд, А. (1949). Тензорное исчисление . Первое издание Dover Publications 1978 года. ISBN 978-0-486-63612-2.
• Кей, Дэвид (апрель 1988). Очерк тензорного исчисления Шаума. McGraw Hill Professional. ISBN 978-0-07-033484-7.

Дальнейшее чтение

• Гупта, Киран Чандра, Классическая механика частиц и твердых тел (Wiley, 1988).
• Кассель, Кевин (2013). Вариационные методы с приложениями в науке и технике . Кембридж: Cambridge University Press. ISBN 978-1-107-02258-4.
• Голдштейн , Герберт и др. Классическая механика . 3-е изд., Пирсон, 2002.

Внешние ссылки

• Дэвид Тонг. "Конспект лекций Кембриджа по классической динамике". DAMTP . Получено 08.06.2017 .
• Принцип наименьшего интерактивного действия Отличное интерактивное объяснение/веб-страница
• Жозеф Луи де Лагранж - Полные произведения (Gallica-Math)
• Ограниченное движение и обобщенные координаты, стр. 4