Логарифм

Математическая функция, обратная показательной функции

Графики функций логарифмирования с тремя часто используемыми основаниями. Особые точки log _b  b = 1 обозначены пунктирными линиями, а все кривые пересекаются в log _b  1 = 0 .

В математике логарифм является функцией , обратной возведению в степень . Это означает, что логарифм числа  x по основанию  b является показателем степени , до которой необходимо возвести b , чтобы получить x . Например, поскольку 1000 = 10 ³ , логарифм по основанию  10 от 1000 равен 3 или log ₁₀  (1000) = 3 . Логарифм от x по основанию  b обозначается как log _b  ( x ) или без круглых скобок, log _b  x , или даже без явного основания, log  x , когда путаница невозможна или когда основание не имеет значения, например, в большое обозначение О.

Логарифм по основанию 10 называется десятичным или десятичным логарифмом и обычно используется в науке и технике. В основе натурального логарифма лежит число  e ≈ 2,718 ; его использование широко распространено в математике и физике из-за его очень простой производной . Двоичный логарифм использует базу 2 и часто используется в информатике .

Логарифмы были введены Джоном Непером в 1614 году как средство упрощения вычислений. ^[1] Они были быстро приняты мореплавателями, учеными, инженерами, геодезистами и другими людьми для облегчения выполнения высокоточных вычислений. Используя таблицы логарифмов , утомительные шаги многозначного умножения можно заменить поиском в таблице и более простым сложением. Это возможно, поскольку логарифм произведения представляет собой сумму логарифмов множителей:

$${\displaystyle \log _{b}(xy)=\log _{b}x+\log _{b}y,}$$

bxyb ≠ 1линейкаЛеонарда Эйлерапоказательной функциейе^[2]

Логарифмические шкалы сводят большие величины к меньшим. Например, децибел (дБ) — это единица измерения отношения в виде логарифмов , в основном для мощности и амплитуды сигнала ( частым примером которых является звуковое давление ). В химии pH — это логарифмическая мера кислотности водного раствора . Логарифмы являются обычным явлением в научных формулах , а также при измерении сложности алгоритмов и геометрических объектов, называемых фракталами . Они помогают описывать соотношения частот музыкальных интервалов , появляются в формулах для подсчета простых чисел или аппроксимации факториалов , служат основой для некоторых моделей в психофизике и могут помочь в судебно-медицинской экспертизе .

Концепция логарифма как обратной возведения в степень распространяется и на другие математические структуры. Однако в общих условиях логарифм имеет тенденцию быть многозначной функцией. Например, комплексный логарифм является многозначной обратной комплексной показательной функции. Точно так же дискретный логарифм является многозначной обратной экспоненциальной функцией в конечных группах; он находит применение в криптографии с открытым ключом .

Мотивация

График логарифма по основанию 2 пересекает ось x в точке x = 1 и проходит через точки (2, 1) , ( 4, 2) и (8, 3) , изображая, например, log ₂ (8) = 3 и 2 ³ = 8 . График подбирается сколь угодно близко к оси Y , но не пересекает ее .

Сложение , умножение и возведение в степень — три наиболее фундаментальные арифметические операции. Обратное действие сложения — вычитание, а обратное умножению — деление . Аналогично, логарифм — это операция, обратная возведению в степень . Возведение в степень - это когда число b , основание , возводится в определенную степень y , показатель степени , чтобы дать значение x ; это обозначается

$${\displaystyle b^{y}=x.}$$

238 ${\displaystyle 2^{3}=8.}$

Логарифм по основанию b — это обратная операция, которая обеспечивает выход y из входа x . То есть это эквивалентно тому , что b является положительным действительным числом . (Если b не является положительным действительным числом, можно определить и возведение в степень, и логарифм, но они могут принимать несколько значений, что значительно усложняет определения.) ${\displaystyle y=\log _{b}x}$ ${\displaystyle x=b^{y}}$

Одной из главных исторических мотиваций введения логарифмов является формула

$${\displaystyle \log _{b}(xy)=\log _{b}x+\log _{b}y,}$$

таблицы логарифмов

Определение

Учитывая положительное действительное число b такое, что b ≠ 1 , логарифм положительного действительного числа x по основанию  b ^{[nb 1]} является показателем степени, на которую b необходимо возвести, чтобы получить x . Другими словами, логарифм x по основанию  b — это уникальное действительное число  y такое, что . ^[3] ${\displaystyle b^{y}=x}$

Логарифм обозначается « log _b  x » (произносится как «логарифм от x по основанию  b », « логарифм по основанию b от x » или чаще всего «логарифм по основанию  b от x »).

Эквивалентное и более краткое определение состоит в том, что функция log _b является функцией, обратной функции . ${\displaystyle x\mapsto b^{x}}$

Примеры

• журнал ₂  16 знак равно 4 , так как 2 ⁴ знак равно 2 × 2 × 2 × 2 знак равно 16 .
• Логарифмы могут быть и отрицательными: поскольку ${\textstyle \log _{2}\!{\frac {1}{2}}=-1}$ ${\textstyle 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}.}$
• log ₁₀  150 составляет примерно 2,176, что лежит между 2 и 3, точно так же, как 150 находится между 10 ² = 100 и 10 ³ = 1000 .
• Для любой базы  b log b _b  = 1 и log _b  1 = 0 , поскольку b ¹ = b и b ⁰ = 1 соответственно.

Логарифмические тождества

Несколько важных формул, иногда называемых логарифмическими тождествами или логарифмическими законами , связывают логарифмы друг с другом. ^[4]

Произведение, частное, степень и корень

Логарифм произведения — это сумма логарифмов умножаемых чисел; логарифм отношения двух чисел — это разность логарифмов. Логарифм p -й степени числа в p  раз больше логарифма самого числа; логарифм корня p -й степени равен логарифму числа, разделенного на p . В следующей таблице перечислены эти личности с примерами. Каждое из тождеств можно получить после подстановки определений логарифмов или в левых частях. ${\displaystyle x=b^{\,\log _{b}x}}$ ${\displaystyle y=b^{\,\log _{b}y}}$

Смена базы

Логарифм log _b  x можно вычислить из логарифмов x и b по произвольному основанию  k , используя следующую формулу: ^{[nb 2]}

$${\displaystyle \log _{b}x={\frac {\log _{k}x}{\log _{k}b}}.}$$

Типичные научные калькуляторы вычисляют логарифмы по основаниям 10 и e . ^[5] Логарифмы по любому основанию  b можно определить, используя любой из этих двух логарифмов по предыдущей формуле:

$${\displaystyle \log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}.}$$

Учитывая число x и его логарифм y = log _b  x до неизвестного основания  b , основание определяется следующим образом:

$${\displaystyle b=x^{\frac {1}{y}},}$$

в чем можно убедиться, возведя определяющее уравнение в степень ${\displaystyle x=b^{\,\log _{b}x}=b^{y}}$ ${\displaystyle {\tfrac {1}{y}}.}$

Особые базы

Графики логарифма по основаниям 0,5, 2 и е

Среди всех вариантов основы особенно распространены три. Это b = 10 , b = e ( иррациональная математическая константа ≈ 2,71828) и b = 2 ( двоичный логарифм ). В математическом анализе логарифм по основанию e широко распространен из-за аналитических свойств, объясненных ниже. С другой стороны, логарифмы по основанию 10 ( десятичный логарифм ) легко использовать для ручных вычислений в десятичной системе счисления: ^[6]

$${\displaystyle \log _{10}(10x)=\log _{10}10+\log _{10}x=1+\log _{10}x.\ }$$

log ₁₀  ( x )десятичных цифрxцелое число,log ₁₀  ( x )^[7]log ₁₀ (1430)теории информациинатуральных чиселбитов^[8]информатикедвоичная систематеории музыкиоктавацентовравнотемперированный полутонфотографиизначений экспозицииуровней освещенностивремени экспозициидиафрагмысветочувствительности пленки^[9]

Многие дисциплины записывают log  x как сокращение от log _b  x , когда предполагаемую базу можно определить на основе контекста или дисциплины (или когда база неопределенна или несущественна). В информатике log обычно относится к log ₂ , а в математике log обычно относится к log _e . ^[10] В других контекстах log часто означает log ₁₀ . ^[11] В следующей таблице перечислены общие обозначения логарифмов по этим основаниям и поля, в которых они используются. В столбце «Обозначение ISO» перечислены обозначения, предложенные Международной организацией по стандартизации ( ISO 80000-2 ). ^[12]

История

В истории логарифмов в Европе XVII века была открыта новая функция , которая расширила сферу анализа за пределы алгебраических методов. Метод логарифмов был публично предложен Джоном Нэпьером в 1614 году в книге под названием Mirifici Logarithmorum Canonis Descriptio ( «Описание чудесного канона логарифмов »). ^{[19] [20]} До изобретения Нэпьера существовали и другие методы аналогичного масштаба, такие как простафаэрез или использование таблиц прогрессий, широко разработанные Йостом Бюрги около 1600 года. ^{[21] [22]} Нэпьер придумал этот термин. для логарифма на среднелатинском языке «логарифм» происходит от греческого слова, буквально означающего «число-отношение», от logos «пропорция, соотношение, слово» + arithmos «число».

Десятый логарифм числа — это показатель той степени десяти, которая равна числу. ^[23] Утверждение о том, что число требует такого количества цифр, является грубым намеком на десятичный логарифм, который Архимед называл «порядком числа». ^[24] Первые действительные логарифмы представляли собой эвристические методы, позволяющие превратить умножение в сложение, что способствовало быстрым вычислениям. В некоторых из этих методов использовались таблицы, полученные на основе тригонометрических тождеств. ^[25] Такие методы называются простафаэрезом .

Изобретение функции, ныне известной как натуральный логарифм, началось как попытка выполнить квадратуру прямоугольной гиперболы Грегуаром де Сен-Винсентом , бельгийским иезуитом, проживающим в Праге. Архимед написал «Квадратуру параболы» в третьем веке до нашей эры, но квадратура гиперболы ускользала от всех попыток, пока Сен-Винсент не опубликовал свои результаты в 1647 году. Связь, которую логарифм обеспечивает между геометрической прогрессией в ее аргументе и арифметической прогрессией. значений, побудило А. А. де Сараса установить связь квадратуры Сен-Венсана и традиции логарифмов в простаферезе , что привело к появлению термина «гиперболический логарифм», синонима натурального логарифма. Вскоре новую функцию оценили Христиан Гюйгенс и Джеймс Грегори . Обозначение Log y было принято Лейбницем в 1675 г. ^[26] и в следующем году он связал его с интегралом ${\textstyle \int {\frac {dy}{y}}.}$

До того, как Эйлер разработал свою современную концепцию комплексных натуральных логарифмов, Роджер Коутс получил почти эквивалентный результат, когда в 1714 году показал, что ^[27]

$${\displaystyle \log(\cos \theta +i\sin \theta )=i\theta .}$$

Таблицы логарифмов, логарифмические линейки и исторические приложения

Объяснение логарифмов в Британской энциклопедии 1797 года.

Упрощая сложные вычисления до того, как стали доступны калькуляторы и компьютеры, логарифмы способствовали развитию науки, особенно астрономии . Они сыграли решающую роль в развитии геодезии , небесной навигации и других областях. Пьер-Симон Лаплас называл логарифмы.

«...[замечательное изобретение, которое, сокращая до нескольких дней многомесячный труд, удваивает жизнь астронома и избавляет его от ошибок и отвращения, неотделимых от долгих вычислений». ^[28]

Поскольку функция f ( x ) = _bx является обратной функцией log  ^bx , ее называют антилогарифмом . ^[29] В настоящее время эту функцию чаще называют показательной функцией .

Таблицы журналов

Ключевым инструментом, позволившим практическое использование логарифмов, была таблица логарифмов . ^[30] Первая такая таблица была составлена ​​Генри Бриггсом в 1617 году, сразу после изобретения Нэпьера, но с новаторским использованием 10 в качестве основы. Первая таблица Бриггса содержала десятичные логарифмы всех целых чисел в диапазоне от 1 до 1000 с точностью до 14 цифр. В дальнейшем были написаны таблицы с увеличивающейся областью применения. В этих таблицах перечислены значения log ₁₀  x для любого числа  x в определенном диапазоне и с определенной точностью. Логарифмы с основанием 10 повсеместно использовались для вычислений, отсюда и название «десятигранный логарифм», поскольку числа, которые отличаются в 10 раз, имеют логарифмы, которые отличаются целыми числами. Десятый логарифм x можно разделить на целую и дробную часть , известную как характеристика и мантисса . В таблицы логарифмов необходимо включать только мантиссу, так как характеристику можно легко определить, посчитав цифры от десятичной точки. ^[31] Характеристика 10 · x равна единице плюс характеристика x , и их мантиссы одинаковы. Таким образом, используя трехзначную таблицу журналов, логарифм 3542 аппроксимируется выражением

$${\displaystyle \log _{10}3542=\log _{10}(1000\cdot 3.542)=3+\log _{10}3.542\approx 3+\log _{10}3.54}$$

Большую точность можно получить интерполяцией :

$${\displaystyle \log _{10}3542\approx 3+\log _{10}3.54+0.2(\log _{10}3.55-\log _{10}3.54)}$$

Значение 10 ^x можно определить путем обратного поиска в той же таблице, поскольку логарифм является монотонной функцией .

Вычисления

Произведение и частное двух положительных чисел c и d обычно рассчитывалось как сумма и разность их логарифмов. Произведение  cd или частное  c / d получено в результате поиска антилогарифма суммы или разности с помощью той же таблицы:

$${\displaystyle cd=10^{\,\log _{10}c}\,10^{\,\log _{10}d}=10^{\,\log _{10}c\,+\,\log _{10}d}}$$

$${\displaystyle {\frac {c}{d}}=cd^{-1}=10^{\,\log _{10}c\,-\,\log _{10}d}.}$$

Для ручных вычислений, требующих сколько-нибудь заметной точности, поиск двух логарифмов, вычисление их суммы или разности и поиск антилогарифма происходит намного быстрее, чем выполнение умножения более ранними методами, такими как простафаэрез , который основан на тригонометрических тождествах .

Вычисления степеней и корней сводятся к умножению или делению и поиску по

$${\displaystyle c^{d}=\left(10^{\,\log _{10}c}\right)^{d}=10^{\,d\log _{10}c}}$$

и

$${\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\log _{10}c}.}$$

Тригонометрические расчеты облегчались таблицами, содержащими десятичные логарифмы тригонометрических функций .

Правила слайдов

Еще одним важным применением была логарифмическая линейка — пара логарифмически разделенных шкал, используемых для вычислений. Нескользящая логарифмическая шкала, правило Гюнтера , была изобретена вскоре после изобретения Нейпира. Уильям Отред усовершенствовал его, создав логарифмическую линейку — пару логарифмических шкал, подвижных относительно друг друга. Числа располагаются на скользящих шкалах на расстояниях, пропорциональных разностям их логарифмов. Соответствующее перемещение верхней шкалы эквивалентно механическому добавлению логарифмов, как показано здесь:

Схематическое изображение логарифмической линейки. Начиная с 2 на нижней шкале, прибавьте расстояние к 3 на верхней шкале, чтобы получить произведение 6. Логарифмическая линейка работает, потому что она отмечена так, что расстояние от 1 до x пропорционально логарифму x .

Например, прибавление расстояния от 1 до 2 на нижней шкале к расстоянию от 1 до 3 на верхней шкале дает произведение 6, которое считывается в нижней части. Логарифмическая линейка была важным расчетным инструментом для инженеров и ученых до 1970-х годов, поскольку она позволяла, за счет точности, выполнять гораздо более быстрые вычисления, чем методы, основанные на таблицах. ^[32]

Аналитические свойства

Более глубокое изучение логарифмов требует понятия функции . Функция — это правило, которое по одному числу дает другое число. ^[33] Примером может служить функция, производящая x -ю степень числа b из любого действительного числа  x , где основание  b является фиксированным числом. Эта функция записывается как f ( x ) = b ^x . Когда b положительно и не равно 1, ниже мы покажем, что f обратимо, если рассматривать его как функцию от действительных чисел к положительным действительным числам.

Существование

Пусть b — положительное действительное число, не равное 1, и пусть f ( x ) = b ^x .

Стандартный результат реального анализа состоит в том, что любая непрерывная строго монотонная функция является биективной между своей областью определения и областью значений. Этот факт следует из теоремы о промежуточном значении . ^[34] Теперь f строго возрастает ( для b > 1 ) или строго убывает (для 0 < b < 1 ), ^[35] является непрерывным, имеет область определения и диапазон . Следовательно, f является биекцией из в . Другими словами, для каждого положительного действительного числа y существует ровно одно действительное число x такое, что . ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} _{>0}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} _{>0}}$ ${\displaystyle b^{x}=y}$

Обозначим через f обратную величину f . То есть log _by — это уникальное действительное число x такое, что . Эта функция называется функцией логарифма по основанию b или логарифмической функцией (или просто логарифмом ). ${\displaystyle \log _{b}\colon \mathbb {R} _{>0}\to \mathbb {R} }$  ${\displaystyle b^{x}=y}$

Характеристика по формуле продукта

Функцию log _b  x можно также существенно охарактеризовать формулой произведения

$${\displaystyle \log _{b}(xy)=\log _{b}x+\log _{b}y.}$$

b > 1возрастающей функцией ff ( b ) = 1^[36]

$${\displaystyle f(xy)=f(x)+f(y).}$$

График функции логарифма

График функции логарифма log _b  ( x ) (синий) получается путем отражения графика функции b ^x (красный) на диагональной линии ( x = y ).

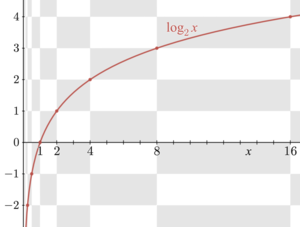
Как обсуждалось выше, функция log _b является обратной экспоненциальной функции . Следовательно, их графики соответствуют друг другу при замене координат x и y (или при отражении от диагональной линии x = y ), как показано справа: точка ( t , u = b ^t ) на графике f дает точку ( u , t = log _b u ) на графике логарифма и наоборот. Как следствие, log _b  ( x ) расходится до бесконечности (становится больше любого заданного числа), если x растет до бесконечности, при условии, что b больше единицы. В этом случае log _b ( x ) — возрастающая функция . Для b < 1 log _b  ( x ) вместо этого стремится к минус бесконечности. Когда x приближается к нулю, log _b x стремится к минус бесконечности для b > 1 (плюс бесконечности для b < 1 соответственно). ${\displaystyle x\mapsto b^{x}}$   

Производная и первообразная

График натурального логарифма (зеленый) и его тангенса при x = 1,5 (черный)

Аналитические свойства функций переходят к обратным к ним. ^[34] Таким образом, поскольку f ( x ) = b ^x является непрерывной и дифференцируемой функцией , то же самое можно сказать и о log _b  y . Грубо говоря, непрерывная функция является дифференцируемой, если ее график не имеет острых «углов». Более того, поскольку производная f ( x ) оценивается как ln( b ) b ^x по свойствам экспоненциальной функции , цепное правило подразумевает , что производная log b _x определяется выражением ^{[35] [37]} 

$${\displaystyle {\frac {d}{dx}}\log _{b}x={\frac {1}{x\ln b}}.}$$

наклонкасающейсяоснованию b( x , log _b  ( x ))1/( x  ln( b ))

Производная ln( x ) равна 1/ x ; это означает, что ln( x ) является единственной первообразной 1 / x , которая имеет значение 0 для x = 1 . Именно эта очень простая формула побудила квалифицировать натуральный логарифм как «натуральный»; это также одна из основных причин важности константы  e .

Производная с обобщенным функциональным аргументом f ( x ) равна

$${\displaystyle {\frac {d}{dx}}\ln f(x)={\frac {f'(x)}{f(x)}}.}$$

логарифмической производнойf' ( x )ln( f ( x ))логарифмическое дифференцирование^[38]натурального логарифма ln( x )^[39]

$${\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C.}$$

Связанные формулы^[40]

Интегральное представление натурального логарифма

Натуральный логарифм t — это заштрихованная область под графиком функции f ( x ) = 1/ x (обратная величина x ).

Натуральный логарифм t можно определить как определенный интеграл :

$${\displaystyle \ln t=\int _{1}^{t}{\frac {1}{x}}\,dx.}$$

ln( t )x1/ xx = 1x = tтеоремы исчисленияln( x )1/ x^[41]ln( tu ) = ln( t ) + ln( u )

$${\displaystyle \ln(tu)=\int _{1}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(1)}{=}}\int _{1}^{t}{\frac {1}{x}}\,dx+\int _{t}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(2)}{=}}\ln(t)+\int _{1}^{u}{\frac {1}{w}}\,dw=\ln(t)+\ln(u).}$$

Равенство (1) разбивает интеграл на две части, а равенство (2) представляет собой замену переменной ( w = x / t ). На иллюстрации ниже разделение соответствует разделению области на желтую и синюю части. Изменение масштаба левой синей области по вертикали на коэффициент  t и уменьшение ее на тот же коэффициент по горизонтали не меняет ее размера. Переместив его соответствующим образом, область снова соответствует графику функции f ( x ) = 1/ x . Следовательно, левая синяя область, которая является интегралом от f ( x ) от t до tu , такая же, как интеграл от 1 до u . Это подтверждает равенство (2) более геометрическим доказательством.

Наглядное доказательство формулы произведения натурального логарифма.

Формула мощности ln( t ^r ) = r ln( t ) может быть получена аналогичным образом:

$${\displaystyle \ln(t^{r})=\int _{1}^{t^{r}}{\frac {1}{x}}dx=\int _{1}^{t}{\frac {1}{w^{r}}}\left(rw^{r-1}\,dw\right)=r\int _{1}^{t}{\frac {1}{w}}\,dw=r\ln(t).}$$

интегрирование подстановкойw = x ^{1/ r}

Сумма по обратным натуральным числам,

$${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}},}$$

гармоническим рядомнатуральным логарифмомnбесконечности

$${\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}-\ln(n),}$$

сходитсяконстанта Эйлера – Маскерони γ = 0,5772...быстрая сортировка^[42]

Трансцендентность логарифма

Действительные числа , не являющиеся алгебраическими , называются трансцендентными ; ^{В [43]} например, π и e являются такими числами, но это не так. Почти все действительные числа трансцендентны. Логарифм является примером трансцендентной функции . Теорема Гельфонда – Шнайдера утверждает, что логарифмы обычно принимают трансцендентные, то есть «трудные» значения. ^[44] ${\displaystyle {\sqrt {2-{\sqrt {3}}}}}$

Расчет

Клавиши логарифма (LOG для основания 10 и LN для основания  e ) на графическом калькуляторе TI-83 Plus.

В некоторых случаях логарифмы легко вычислить, например, log ₁₀  (1000) = 3 . В общем, логарифмы можно вычислять с использованием степенного ряда или среднего арифметико-геометрического значения или получать их из предварительно рассчитанной таблицы логарифмов , обеспечивающей фиксированную точность. ^{[45] [46]} Метод Ньютона , итерационный метод приближенного решения уравнений, также может использоваться для вычисления логарифма, поскольку его обратная функция, показательная функция, может быть вычислена эффективно. ^[47] Используя справочные таблицы, CORDIC -подобные методы можно использовать для вычисления логарифмов, используя только операции сложения и битового сдвига . ^{[48] ​​[49]} Более того, алгоритм двоичного логарифма вычисляет lb( x ) рекурсивно , на основе повторного возведения в квадрат x , используя соотношение

$${\displaystyle \log _{2}\left(x^{2}\right)=2\log _{2}|x|.}$$

Силовая серия

Серия Тейлора

Ряд Тейлора ln( z ) с центром в z = 1 . На анимации показаны первые 10 приближений, а также 99-е и 100-е. Приближения не сходятся дальше, чем на расстоянии 1 от центра.

Для любого действительного числа z , удовлетворяющего условию 0 < z ≤ 2 , справедлива следующая формула: ^{[nb 5] [50]}

$${\displaystyle {\begin{aligned}\ln(z)&={\frac {(z-1)^{1}}{1}}-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}}-{\frac {(z-1)^{4}}{4}}+\cdots \\&=\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {(z-1)^{k}}{k}}.\end{aligned}}}$$

Приравнивание функции ln( z ) к этой бесконечной сумме ( ряду ) — это сокращение, говорящее о том, что функция может быть приближена к более и более точному значению с помощью следующих выражений (известных как частичные суммы ):

$${\displaystyle (z-1),\ \ (z-1)-{\frac {(z-1)^{2}}{2}},\ \ (z-1)-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}},\ \ldots }$$

Например, при z = 1,5 третье приближение дает 0,4167 , что примерно на 0,011 больше, чем ln(1,5) = 0,405465 , а девятое приближение дает 0,40553 , что всего лишь примерно на 0,0001 больше. n - я частичная сумма может аппроксимировать ln( z ) с произвольной точностью, при условии, что количество слагаемых n достаточно велико.

В элементарном исчислении говорят, что ряд сходится к функции ln( z ) , а эта функция является пределом ряда. Это ряд Тейлора натурального логарифма в точке z = 1 . Ряд Тейлора для ln( z ) обеспечивает особенно полезное приближение к ln(1 + z ), когда z мало, | г | < 1 , с тех пор

$${\displaystyle \ln(1+z)=z-{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}-\cdots \approx z.}$$

Например, при z = 0,1 аппроксимация первого порядка дает ln(1,1) ≈ 0,1 , что менее чем на 5% отличается от правильного значения 0,0953 .

Обратный гиперболический тангенс

Другой ряд основан на обратной функции гиперболического тангенса :

$${\displaystyle \ln(z)=2\cdot \operatorname {artanh} \,{\frac {z-1}{z+1}}=2\left({\frac {z-1}{z+1}}+{\frac {1}{3}}{\left({\frac {z-1}{z+1}}\right)}^{3}+{\frac {1}{5}}{\left({\frac {z-1}{z+1}}\right)}^{5}+\cdots \right),}$$

z > 0^{[nb 6] [50]}сигма-нотацию

$${\displaystyle \ln(z)=2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {z-1}{z+1}}\right)^{2k+1}.}$$

zz = 1,5ln(1,5)3 × 10 ^-6zy ≈ ln( z )

$${\displaystyle A={\frac {z}{\exp(y)}},}$$

равен

$${\displaystyle \ln(z)=y+\ln(A).}$$

yAAэкспоненциального рядаyzzz = a · 10 ^bln( z ) = ln( a ) + b · ln(10)

Близко связанный метод можно использовать для вычисления логарифма целых чисел. Из приведенной выше серии следует, что: ${\displaystyle \textstyle z={\frac {n+1}{n}}}$

$${\displaystyle \ln(n+1)=\ln(n)+2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {1}{2n+1}}\right)^{2k+1}.}$$

n , то этот ряд дает быстро сходящийся ряд для log( n +1)сходимости ${\textstyle \left({\frac {1}{2n+1}}\right)^{2}}$

Среднее арифметико-геометрическое приближение

Среднее арифметико -геометрическое дает высокоточные аппроксимации натурального логарифма . Сасаки и Канада показали в 1982 году, что он особенно быстр для точности от 400 до 1000 десятичных знаков, в то время как методы рядов Тейлора обычно работают быстрее, когда требуется меньшая точность. В их работе ln( x ) аппроксимируется с точностью 2 ^{− p} (или p  точных битов) по следующей формуле (принадлежащей Карлу Фридриху Гауссу ): ^{[51] [52]}

$${\displaystyle \ln(x)\approx {\frac {\pi }{2\,\mathrm {M} \!\left(1,2^{2-m}/x\right)}}-m\ln(2).}$$

Здесь M( x , y ) обозначает среднее арифметико- геометрическое x и y . Оно получается путем многократного вычисления среднего значения ( x + y )/2 ( среднее арифметическое ) и ( среднее геометрическое ) x и y , после чего эти два числа становятся следующими x и y . Эти два числа быстро сходятся к общему пределу, который является значением M( x , y ) . m выбрано таким, что ${\textstyle {\sqrt {xy}}}$

$${\displaystyle x\,2^{m}>2^{p/2}.\,}$$

для обеспечения необходимой точности. Увеличение m приводит к тому, что вычисление M( x , y ) занимает больше шагов (исходные x и y находятся дальше друг от друга, поэтому для сходимости требуется больше шагов), но дает большую точность. Константы π и ln(2) можно вычислить с помощью быстро сходящихся рядов.

Алгоритм Фейнмана

Работая в Лос-Аламосской национальной лаборатории над Манхэттенским проектом , Ричард Фейнман разработал алгоритм побитовой обработки для вычисления логарифма, который аналогичен делению в столбики и позже использовался в машине соединений . Алгоритм использует тот факт, что каждое действительное число 1 < x < 2 можно представить в виде произведения различных множителей вида 1 + 2 ^{− k} . Алгоритм последовательно строит этот продукт  P , начиная с P = 1 и k = 1 : если P · (1 + 2 ^{− k} ) < x , то он заменяет P на P · (1 + 2 ^{− k} ) . Затем оно увеличивается на единицу независимо от этого. Алгоритм останавливается, когда k становится достаточно большим, чтобы обеспечить желаемую точность. Поскольку log( x ) представляет собой сумму членов формы log(1 + 2 ^{− k} ) , соответствующих тем k , для которых фактор 1 + 2 ^{− k} был включен в произведение  P , log( x ) можно вычислить по формуле простое сложение с использованием таблицы log(1 + 2 ^{− k} ) для всех k . Для таблицы логарифмов можно использовать любое основание. ^[53] ${\displaystyle k}$

Приложения

Раковина наутилуса с изображением логарифмической спирали.

Логарифмы имеют множество приложений внутри и за пределами математики. Некоторые из этих явлений связаны с понятием масштабной инвариантности . Например, каждая камера раковины наутилуса является приблизительной копией следующей, увеличенной в постоянный коэффициент. Это приводит к возникновению логарифмической спирали . ^[54] Закон Бенфорда о распределении старших цифр также можно объяснить масштабной инвариантностью. ^[55] Логарифмы также связаны с самоподобием . Например, логарифмы появляются при анализе алгоритмов, которые решают проблему путем разделения ее на две похожие меньшие проблемы и исправления их решений. ^[56] Размеры самоподобных геометрических фигур, то есть фигур, части которых напоминают общую картину, также основаны на логарифмах. Логарифмические шкалы полезны для количественной оценки относительного изменения значения, а не его абсолютной разницы. Более того, поскольку логарифмическая функция log( x ) растет очень медленно при больших x , логарифмические масштабы используются для сжатия крупномасштабных научных данных. Логарифмы также встречаются во многих научных формулах, таких как уравнение ракеты Циолковского , уравнение Фенске или уравнение Нернста .

Логарифмическая шкала

Логарифмическая диаграмма, показывающая стоимость одной золотой марки в папьермарках во время немецкой гиперинфляции в 1920-х годах.

Научные величины часто выражаются в виде логарифмов других величин в логарифмической шкале . Например, децибел — это единица измерения , связанная с величинами логарифмического масштаба . Он основан на десятичном десятичном десятичном логарифме коэффициента мощности или в 20 раз большем десятичном логарифме коэффициента трансформации . Он используется для количественной оценки потерь уровней напряжения при передаче электрических сигналов, ^[57] для описания уровней мощности звуков в акустике , ^[58] и поглощения света в областях спектрометрии и оптики . Отношение сигнал /шум , характеризующее количество нежелательного шума по отношению к (значимому) сигналу , также измеряется в децибелах. ^[59] Аналогично, пиковое отношение сигнал/шум обычно используется для оценки качества звука и методов сжатия изображения с использованием логарифма. ^[60]

Силу землетрясения измеряют путем десятеричного логарифма энергии, излучаемой при землетрясении. Это используется в моментной шкале магнитуд или шкале магнитуд Рихтера . Например, землетрясение магнитудой 5,0 высвобождает в 32 раза больше (10 ^1,5 ) , а землетрясение магнитудой 6,0 — в 1000 раз (10 ³ ) больше энергии, чем землетрясение магнитудой 4,0. ^[61] Видимая звездная величина измеряет яркость звезд логарифмически. ^[62] В химии отрицательный знак десятичного логарифма, десятичныйкологарифм , обозначается буквой р. ^[63]Например,pH— это десятичный колорарифм активностиионовгидроксония(формаионовводорода H ⁺
набрать воды). ^[64] Активность ионов гидроксония в нейтральной воде составляет 10 ^-7  моль·л ^-1 , следовательно, pH равен 7. Уксус обычно имеет pH около 3. Разница в 4 соответствует соотношению активности 10 ⁴ , то есть активность ионов гидроксония в уксусе составляет около 10 ^-3 моль·л ^-1 .

Полулогарифмические (логарифмически-линейные) графики используют для визуализации концепцию логарифмического масштаба: одна ось, обычно вертикальная, масштабируется логарифмически. Например, на диаграмме справа резкий рост с 1 миллиона до 1 триллиона сжимается до того же места (по вертикальной оси), что и рост с 1 до 1 миллиона. На таких графиках показательные функции вида f ( x ) = a · b ^x выглядят как прямые линии с наклоном , равным логарифму b . Логарифмические графики масштабируют обе оси логарифмически, что приводит к тому, что функции вида f ( x ) = a · x ^k изображаются в виде прямых линий с наклоном, равным показателю степени  k . Это применяется при визуализации и анализе степенных законов . ^[65]

Психология

Логарифмы встречаются в нескольких законах, описывающих человеческое восприятие : ^{[66] [67]} Закон Хика предлагает логарифмическое соотношение между временем, которое люди тратят на выбор альтернативы, и количеством вариантов выбора, которые у них есть. ^[68] Закон Фиттса предсказывает, что время, необходимое для быстрого перемещения к целевой области, является логарифмической функцией расстояния до цели и ее размера. ^[69] В психофизике закон Вебера -Фехнера предполагает логарифмическую связь между стимулом и ощущением , например, фактический и воспринимаемый вес предмета, который несет человек. ^[70] (Однако этот «закон» менее реалистичен, чем более поздние модели, такие как степенной закон Стивенса . ^[71] )

Психологические исследования показали, что люди с небольшим математическим образованием склонны оценивать величины логарифмически, то есть располагать число на неотмеченной линии в соответствии с его логарифмом, так что 10 располагается так же близко к 100, как 100 к 1000. Повышение уровня образования меняет это положение. к линейной оценке (расположение 1000 в 10 раз дальше) в некоторых случаях, тогда как логарифмы используются, когда числа, которые нужно нанести на график, трудно построить линейно. ^{[72] [73]}

Теория вероятностей и статистика

Три функции плотности вероятности (PDF) случайных величин с логнормальным распределением. Параметр местоположения  μ , который равен нулю для всех трех показанных PDF-файлов, является средним значением логарифма случайной величины, а не средним значением самой переменной.

Распределение первых цифр (в %, красные столбцы) среди населения 237 стран мира. Черные точки указывают на распределение, предсказанное законом Бенфорда.

Логарифмы возникают в теории вероятностей : закон больших чисел диктует, что для честной монеты , когда количество подбрасываний монеты увеличивается до бесконечности, наблюдаемая доля орлов приближается к половине . Колебания этой доли примерно на половину описываются законом повторного логарифма . ^[74]

Логарифмы также встречаются в логнормальных распределениях . Когда логарифм случайной величины имеет нормальное распределение , говорят, что переменная имеет логнормальное распределение. ^[75] Логнормальные распределения встречаются во многих областях, где переменная формируется как произведение многих независимых положительных случайных величин, например, при изучении турбулентности. ^[76]

Логарифмы используются для оценки максимального правдоподобия параметрических статистических моделей . Для такой модели функция правдоподобия зависит как минимум от одного параметра , который необходимо оценить. Максимум функции правдоподобия возникает при том же значении параметра, что и максимум логарифма правдоподобия («логарифм правдоподобия »), поскольку логарифм является возрастающей функцией. Логарифмическое правдоподобие легче максимизировать, особенно для умноженных правдоподобий для независимых случайных величин. ^[77]

Закон Бенфорда описывает появление цифр во многих наборах данных , например, в высотах зданий. Согласно закону Бенфорда, вероятность того, что первая десятичная цифра элемента в выборке данных равна d (от 1 до 9), равна log ₁₀  ( d + 1) − log ₁₀  ( d ) независимо от единицы измерения. ^[78] Таким образом, можно ожидать, что около 30% данных будут иметь 1 в качестве первой цифры, 18% начинаются с 2 и т. д. Аудиторы проверяют отклонения от закона Бенфорда для выявления мошенничества в бухгалтерском учете. ^[79]

Преобразование логарифма — это тип преобразования данных , используемый для приближения эмпирического распределения к предполагаемому.

Вычислительная сложность

Анализ алгоритмов — это раздел информатики , изучающий производительность алгоритмов (компьютерных программ , решающих определенную задачу). ^[80] Логарифмы полезны для описания алгоритмов, которые делят проблему на более мелкие и объединяют решения подзадач. ^[81]

Например, чтобы найти число в отсортированном списке, алгоритм двоичного поиска проверяет среднюю запись и переходит к половине до или после средней записи, если число все еще не найдено. Этот алгоритм требует в среднем log ₂  ( N ) сравнений, где N — длина списка. ^[82] Аналогично, алгоритм сортировки слиянием сортирует несортированный список, разделяя его на половины и сортируя их перед объединением результатов. Алгоритмы сортировки слиянием обычно требуют времени , примерно пропорционального N · log( N ) . ^[83] Здесь не указано основание логарифма, поскольку результат изменяется только на постоянный коэффициент при использовании другого основания. Постоянный коэффициент обычно не учитывается при анализе алгоритмов в рамках стандартной модели единой стоимости . ^[84]

Говорят, что функция  f ( x ) растет логарифмически, если f ( x ) (точно или приблизительно) пропорциональна логарифму x . (Однако в биологических описаниях роста организма этот термин используется для обозначения экспоненциальной функции. ^[85] ). Например, любое натуральное число  N может быть представлено в двоичной форме не более чем в log ₂  N + 1  бит . Другими словами, объем памяти , необходимый для хранения N , растет логарифмически с ростом N.

Энтропия и хаос

Бильярд на овальном бильярдном столе . Две частицы, начиная с центра под углом, отличающимся на один градус, проходят пути, хаотически расходящиеся из-за отражений на границе.

Энтропия в широком смысле является мерой беспорядка некоторой системы. В статистической термодинамике энтропия  S некоторой физической системы определяется как

$${\displaystyle S=-k\sum _{i}p_{i}\ln(p_{i}).\,}$$

ip _ii , а kпостоянная Больцманаэнтропия в теории информацииNlog ₂  N^[86]

Показатели Ляпунова используют логарифмы для измерения степени хаотичности динамической системы . Например, для частицы, движущейся по овальному бильярдному столу, даже небольшие изменения начальных условий приводят к совершенно разным траекториям частицы. Такие системы детерминированно хаотичны , поскольку небольшие ошибки измерения начального состояния предсказуемо приводят к существенно отличающимся конечным состояниям . ^[87] По крайней мере один показатель Ляпунова детерминированно хаотической системы положителен.

Фракталы

Треугольник Серпинского (справа) построен путем многократной замены равносторонних треугольников тремя меньшими.

Логарифмы встречаются в определениях размерности фракталов . ^[88] Фракталы — это геометрические объекты, которые самоподобны в том смысле, что небольшие части воспроизводят, хотя бы грубо, всю глобальную структуру. Треугольник Серпинского (на фото) может быть покрыт тремя копиями самого себя, каждая из которых имеет стороны, равные половине исходной длины. Это делает хаусдорфову размерность этой структуры ln(3)/ln(2) ≈ 1,58 . Другое понятие размерности, основанное на логарифме, получается путем подсчета количества ячеек, необходимых для покрытия рассматриваемого фрактала.

Музыка

Четыре разные октавы показаны в линейном масштабе, затем показаны в логарифмическом масштабе (так, как их слышит ухо).

Логарифмы связаны с музыкальными тонами и интервалами . При равной темперации соотношение частот зависит только от интервала между двумя тонами, а не от конкретной частоты или высоты отдельных тонов. Например, нота  ля имеет частоту 440  Гц , а си-бемоль — 466 Гц. Интервал между ля и си-бемоль составляет полутон , как и интервал между си-бемоль и си (частота 493 Гц). Соответственно, соотношения частот совпадают:

$${\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.}$$

основанию 2 ^1/12 отношения частотоснованию 2 ^1/1200центах.^[89]

Теория чисел

Натуральные логарифмы тесно связаны с подсчетом простых чисел (2, 3, 5, 7, 11, ...), что является важной темой теории чисел . Для любого целого числа  x количество простых чисел , меньших или равных x , обозначается π ( x ) . Теорема о простых числах утверждает, что π ( x ) приблизительно определяется выражением

$${\displaystyle {\frac {x}{\ln(x)}},}$$

π ( x )x^[90]xпропорциональнаxπ ( x )логарифмической интегральнойLi( x )

$${\displaystyle \mathrm {Li} (x)=\int _{2}^{x}{\frac {1}{\ln(t)}}\,dt.}$$

Риманагипотезπ ( x )Li( x )^[91]Эрдеша-Кацапростых множителей,натуральный логарифм

Логарифм факториала n , n ! = 1 · 2 · ... · n , определяется выражением

$${\displaystyle \ln(n!)=\ln(1)+\ln(2)+\cdots +\ln(n).}$$

формулы Стирлингаn ! n^[92]

Обобщения

Комплексный логарифм

Полярная форма z = x + iy . И φ , и φ' являются аргументами z .

Все комплексные числа a , которые решают уравнение

$${\displaystyle e^{a}=z}$$

называются комплексными логарифмами z , когда z (считается) комплексным числом. Комплексное число обычно представляется как z = x + iy , где x и y — действительные числа, а i — мнимая единица , квадрат которой равен −1. Такое число можно визуализировать с помощью точки на комплексной плоскости , как показано справа. Полярная форма кодирует ненулевое комплексное число  z его абсолютным значением , то есть (положительным, действительным) расстоянием  r до начала координат и углом между вещественной осью ( x ) Re и линией, проходящей через оба начала координат. и з . Этот угол называется аргументом z . 

Абсолютное значение r z определяется выражением

$${\displaystyle \textstyle r={\sqrt {x^{2}+y^{2}}}.}$$

Используя геометрическую интерпретацию синуса и косинуса и их периодичность в 2 π , любое комплексное число  z можно обозначить как

$${\displaystyle z=x+iy=r(\cos \varphi +i\sin \varphi )=r(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )),}$$

для любого целого числа  k . Очевидно, аргумент z не определен однозначно: и φ , и φ' = φ + 2 k π являются допустимыми аргументами z для всех целых чисел  k , поскольку добавление 2 k π  радиан или k ⋅ ​​360° ^{[nb 7]} к φ соответствует «обмотка» вокруг начала координат против часовой стрелки на k  витков . Результирующее комплексное число всегда равно z , как показано справа для k = 1 . Можно выбрать ровно один из возможных аргументов z в качестве так называемого главного аргумента , обозначаемого Arg( z ) с заглавной буквы  A , потребовав, чтобы φ принадлежал одному, удобно выбранному повороту, например - π < φ ≤ π ^{[ 93]} или 0 ≤ φ < 2 π . ^[94] Эти области, где аргумент z определяется однозначно, называются ветвями функции аргумента.

Главная ветвь (- π , π ) комплексного логарифма Log( z ) . Черная точка при z = 1 соответствует нулевому абсолютному значению, а более яркие цвета относятся к большим абсолютным значениям. Оттенок цвета кодирует аргумент Log( z ) .

Формула Эйлера связывает тригонометрические функции синус и косинус с комплексной экспонентой :

$${\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi .}$$

Используя эту формулу и снова периодичность, справедливы следующие тождества: ^[95]

$${\displaystyle {\begin{array}{lll}z&=&r\left(\cos \varphi +i\sin \varphi \right)\\&=&r\left(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )\right)\\&=&re^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)}e^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)+i(\varphi +2k\pi )}=e^{a_{k}},\end{array}}}$$

где ln( r ) — уникальный действительный натуральный логарифм, a _k обозначает комплексный логарифм z , а k — произвольное целое число. Следовательно, комплексные логарифмы z , которые представляют собой все те комплексные значения a _k , для которых a k _- я  степень e равна z , представляют собой бесконечное множество значений.

${\displaystyle a_{k}=\ln(r)+i(\varphi +2k\pi ),\quad }$для произвольных целых чисел  k .

Если взять k так, что φ + 2 k π находится в пределах определенного интервала для главных аргументов, тогда a _k называется главным значением логарифма, обозначаемым Log( z ) , опять же с заглавной буквы  L . Главный аргумент любого положительного действительного числа  x равен 0; следовательно, Log( x ) является действительным числом и равен действительному (натуральному) логарифму. Однако приведенные выше формулы для логарифмов произведений и степеней не обобщаются на главное значение комплексного логарифма. ^[96]

На иллюстрации справа изображен Log( z ) , ограничивающий аргументы z интервалом (−π, π] . Таким образом, соответствующая ветвь комплексного логарифма имеет разрывы по всей отрицательной действительной оси x  , что можно увидеть на рисунке. скачок оттенка там. Этот разрыв возникает из-за перехода на другую границу в той же ветви при пересечении границы, т. е. без перехода на соответствующее значение k непрерывно соседней ветви. Такой локус называется разрезом ветки . Отказ от ограничений диапазона аргумента делает отношения «аргумент z » и, следовательно, «логарифм z » многозначными функциями .

Обратные к другим экспоненциальным функциям

Возведение в степень происходит во многих областях математики, и его обратную функцию часто называют логарифмом. Например, логарифм матрицы — это (многозначная) обратная функция матричной экспоненты . ^[97] Другим примером является p -адический логарифм , обратная функция p -адической экспоненты . Оба определяются через ряд Тейлора, аналогичный реальному случаю. ^[98] В контексте дифференциальной геометрии экспоненциальное отображение отображает касательное пространство в точке многообразия в окрестность этой точки. Ее обратную карту также называют логарифмической (или логарифмической) картой. ^[99]

В контексте конечных групп возведение в степень задается путем многократного умножения одного элемента группы  b на самого себя. Дискретный логарифм — это целое число  n , решающее уравнение

$${\displaystyle b^{n}=x,}$$

xкриптографии с открытым ключомобмене ключами Диффи-Хеллманакриптографическими^[100] Логарифм Зехаполя^[101]

Другие обратные функции, подобные логарифму, включают двойной логарифм  ln(ln( x )) , супер- или гипер-4-логарифм (небольшая вариация которого в информатике называется повторным логарифмом ), функцию Ламберта W и логит. . Они являются обратными функциями двойной экспоненциальной функции , тетрации , f ( w ) = we ^w , ^[102] и логистической функции соответственно. ^[103]

Связанные понятия

С точки зрения теории групп , тождество log( cd ) = log( c ) + log( d ) выражает групповой изоморфизм между положительными вещественными числами при умножении и вещественными числами при сложении. Логарифмические функции — единственные непрерывные изоморфизмы между этими группами. ^[104] Благодаря этому изоморфизму мера Хаара ( мера Лебега )  dx на вещественных числах соответствует мере Хаара  dx / x на положительных вещественных числах. ^[105] Неотрицательные действительные числа не только допускают умножение, но и сложение, и образуют полукольцо , называемое вероятностным полукольцом ; на самом деле это полуполе . Затем логарифм преобразует умножение в сложение (логарифмическое умножение) и сложение в логарифмическое сложение ( LogSumExp ), давая изоморфизм полуколец между вероятностным полукольцом и логарифмическим полукольцом .

Логарифмические одноформы  df / f появляются в комплексном анализе и алгебраической геометрии как дифференциальные формы с логарифмическими полюсами . ^[106]

Полилогарифм — это функция, определяемая формулой

$${\displaystyle \operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}}.}$$

натуральным логарифмомLi ₁  ( z ) = −ln(1 − z )Li _s  (1)дзета-функции Римана ζ( s )^[107]

Смотрите также

• Математический портал
• Арифметический портал
• Химический портал
• Географический портал
• Инженерный портал

• Десятичный показатель (dex)
• Экспоненциальная функция
• Указатель статей о логарифмах

Примечания

1. Ограничения на x и b описаны в разделе «Аналитические свойства».
2. Доказательство: логарифмируя по основанию k определяющее тождество, получаем формулу. ${\textstyle x=b^{\log _{b}x},}$ ${\displaystyle \log _{k}x=\log _{k}\left(b^{\log _{b}x}\right)=\log _{b}x\cdot \log _{k}b.}$ ${\displaystyle \log _{b}x.}$
3. Некоторые математики не одобряют это обозначение. В своей автобиографии 1985 года Пол Халмос раскритиковал то, что он считал «детскими обозначениями», которые, по его словам, никогда не использовал ни один математик. ^[15] Обозначение было изобретено математиком Ирвингом Стрингхэмом . ^{[16] [17]}
4. Например , C , Java , Haskell и BASIC .
5. Тот же ряд справедлив для главного значения комплексного логарифма для комплексных чисел z , удовлетворяющих | г - 1| < 1 .
6. Тот же ряд справедлив для главного значения комплексного логарифма для комплексных чисел z с положительной действительной частью.
7. См. преобразование между 2 π и 360 градусами в радианах .

Рекомендации

1. Хобсон, Эрнест Уильям (1914), Джон Нэпьер и изобретение логарифмов, 1614; лекция, Библиотеки Калифорнийского университета, Кембридж: University Press
2. Реммерт, Рейнхольд. (1991), Теория комплексных функций , Нью-Йорк: Springer-Verlag, ISBN. 0387971955, OCLC  21118309
3. Кейт, СК; Бхапкар, HR (2009), Основы математики, Пуна: Технические публикации, ISBN 978-81-8431-755-8^{[ постоянная мертвая ссылка ]} , глава 1
4. Все утверждения в этом разделе можно найти в Шаилеше Ширали 2002, раздел 4 (Дуглас Даунинг 2003, стр. 275) или Кейт и Бхапкар 2009, стр. 275. Например, 1-1.
5. Бернштейн, Стивен; Бернштейн, Рут (1999), Очерк теории и проблем элементов статистики Шаума. I, Описательная статистика и вероятность, серия обзоров Шаума, Нью-Йорк: McGraw-Hill , ISBN 978-0-07-005023-5, п. 21
6. Даунинг, Дуглас (2003), Легкая алгебра, Образовательная серия Бэррона, Хоппож, Нью-Йорк: Barron's, ISBN 978-0-7641-1972-9, глава 17, с. 275
7. Вегенер, Инго (2005), Теория сложности: исследование пределов эффективных алгоритмов , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-21045-0, п. 20
8. Ван дер Люббе, Ян Калифорния (1997), Теория информации, Cambridge University Press, стр. 3, ISBN 978-0-521-46760-5
9. Аллен, Элизабет; Триантафиллиду, Софи (2011), Руководство по фотографии, Тейлор и Фрэнсис, стр. 228, ISBN 978-0-240-52037-7
10. Гудрич, Майкл Т .; Тамассиа, Роберто (2002), Разработка алгоритмов: основы, анализ и примеры из Интернета , John Wiley & Sons, стр. 23. Одним из интересных и иногда даже удивительных аспектов анализа структур данных и алгоритмов является повсеместное присутствие логарифмов... По обычаю в компьютерной литературе мы опускаем запись основания b логарифма при b = 2. .
11. Паркхерст, Дэвид Ф. (2007), Введение в прикладную математику для науки об окружающей среде (иллюстрированное издание), Springer Science & Business Media, стр. 288, ISBN 978-0-387-34228-3
12. Количества и единицы измерения – Часть 2: Математика (ISO 80000-2:2019); ЭН ИСО 80000-2
13. Гуллберг, Январь (1997), Математика: от рождения чисел. , Нью-Йорк: WW Norton & Co, ISBN. 978-0-393-04002-9
14. См. сноску 1 в Perl, Иегошуа; Рейнгольд, Эдвард М. (декабрь 1977 г.), «Понимание сложности интерполяционного поиска», Information Processing Letters , 6 (6): 219–22, doi : 10.1016/0020-0190(77)90072-2
15. Пол Халмос (1985), Я хочу быть математиком: автоматография , Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-0-387-96078-4
16. Ирвинг Стрингхэм (1893), Унипланарная алгебра: часть I пропедевтики высшего математического анализа, The Berkeley Press, стр. xiii
17. Рой С. Фридман (2006), Введение в финансовые технологии, Амстердам: Academic Press, стр. 59, ISBN 978-0-12-370478-8
18. См. Теорему 3.29 в книге Рудин, Уолтер (1984), Принципы математического анализа (3-е изд., Изд. иностранных студентов), Окленд: McGraw-Hill International, ISBN. 978-0-07-085613-4
19. Нэпьер, Джон (1614), Mirifici Logarithmorum Canonis Descriptio [ Описание чудесного канона логарифмов ] (на латыни), Эдинбург, Шотландия: Эндрю Харт
    Продолжение ... Constructio было опубликовано посмертно:
    Нэпьер, Джон (1619), Mirifici Logarithmorum Canonis Constructio [ Построение чудесного правила логарифмов ] (на латыни), Эдинбург: Эндрю Харт
    Ян Брюс сделал аннотированный перевод обеих книг (2012 г.), доступный на сайте 17 Centurymaths.com.
20. Хобсон, Эрнест Уильям (1914), Джон Нэпьер и изобретение логарифмов, 1614, Кембридж: The University Press
21. Фолкертс, Менсо; Лаунерт, Дитер; Том, Андреас (2016), «Метод Йоста Бюрги для вычисления синусов», Historia Mathematica , 43 (2): 133–147, arXiv : 1510.03180 , doi : 10.1016/j.hm.2016.03.001, MR  3489006, S2CID  119326088
22. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Йост Бюрги (1552–1632)», Архив истории математики MacTutor , Университет Сент-Эндрюс
23. Уильям Гарднер (1742) Таблицы логарифмов
24. Пирс, Р. К. младший (январь 1977 г.), «Краткая история логарифмов», The Two-Year College Mathematics Journal , 8 (1): 22–26, doi : 10.2307/3026878, JSTOR  3026878
25. Энрике Гонсалес-Веласко (2011) Путешествие по математике - творческие эпизоды в ее истории , §2.4 Гиперболические логарифмы, стр. 117, ISBN Спрингера 978-0-387-92153-2 
26. Флориан Каджори (1913) «История понятий экспоненты и логарифма», American Mathematical Monthly 20: 5, 35, 75, 107, 148, 173, 205.
27. Стиллвелл, Дж. (2010), Математика и ее история (3-е изд.), Springer
28. Брайант, Уолтер В. (1907), История астрономии, Лондон: Methuen & Co., п. 44
29. Абрамовиц, Милтон ; Стегун, Ирен А. , ред. (1972), Справочник по математическим функциям с формулами, графиками и математическими таблицами (10-е изд.), Нью-Йорк: Dover Publications , ISBN 978-0-486-61272-0, раздел 4.7., с. 89
30. Кэмпбелл-Келли, Мартин (2003), История математических таблиц: от Шумера до электронных таблиц , Оксфордская стипендия онлайн, Oxford University Press , ISBN 978-0-19-850841-0, раздел 2
31. Шпигель, Мюррей Р.; Мойер, RE (2006), Обзор студенческой алгебры Шаума , серия обзоров Шаума , Нью-Йорк: McGraw-Hill , ISBN 978-0-07-145227-4, п. 264
32. Маор, Эли (2009), E: История числа , Princeton University Press , разделы 1, 13, ISBN 978-0-691-14134-3
33. Девлин, Кейт (2004), Множества, функции и логика: введение в абстрактную математику , Математика Чепмена и Холла / CRC (3-е изд.), Бока-Ратон, Флорида: Chapman & Hall / CRC, ISBN 978-1-58488-449-1или посмотрите ссылки в функции
34. Ланг, Серж (1997), Анализ бакалавриата , Тексты для бакалавров по математике (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag , doi : 10.1007/978-1-4757-2698-5, ISBN 978-0-387-94841-6, МР  1476913, раздел III.3
35. Lang 1997, раздел IV.2.
36. Дьедонне, Жан (1969), Основы современного анализа , том. 1, Академик Пресс, с. 84пункт (4.3.1)
37. «Расчет d/dx(Log(b,x))», Wolfram Alpha , Wolfram Research , получено 15 марта 2011 г.
38. Клайн, Моррис (1998), Исчисление: интуитивный и физический подход , Дуврские книги по математике, Нью-Йорк: Dover Publications , ISBN 978-0-486-40453-0, п. 386
39. «Расчет интегрирования (ln (x))», Wolfram Alpha , Wolfram Research , получено 15 марта 2011 г.
40. Абрамовиц и Стегун, ред. 1972, с. 69
41. Курант, Ричард (1988), Дифференциальное и интегральное исчисление. Том. Я , Библиотека классики Wiley, Нью-Йорк: John Wiley & Sons , ISBN 978-0-471-60842-4, МР  1009558, раздел III.6
42. Хэвил, Джулиан (2003), Гамма: изучение постоянной Эйлера , Princeton University Press , ISBN 978-0-691-09983-5, разделы 11.5 и 13.8
43. Номидзу, Кацуми (1996), Избранные статьи по теории чисел и алгебраической геометрии, том. 172, Провиденс, Род-Айленд: Книжный магазин AMS, с. 21, ISBN 978-0-8218-0445-2
44. Бейкер, Алан (1975), Теория трансцендентных чисел , Cambridge University Press , ISBN 978-0-521-20461-3, п. 10
45. Мюллер, Жан-Мишель (2006), Элементарные функции (2-е изд.), Бостон, Массачусетс: Birkhäuser Boston, ISBN 978-0-8176-4372-0, разделы 4.2.2 (с. 72) и 5.5.2 (с. 95)
46. Харт; Чейни; Лоусон; и другие. (1968), Компьютерные аппроксимации , серия SIAM по прикладной математике, Нью-Йорк: Джон Уайли, раздел 6.3, стр. 105–11.
47. Чжан, М.; Дельгадо-Фриас, JG; Василиадис, С. (1994), «Табличная схема Ньютона для высокоточной генерации логарифмов», IEE Proceedings - Computers and Digital Techniques , 141 (5): 281–92, doi : 10.1049/ip-cdt: 19941268, ISSN  1350- 2387, раздел 1 для обзора
48. Меггитт, Дж. Э. (апрель 1962 г.), «Псевдоделение и процессы псевдоумножения», IBM Journal of Research and Development , 6 (2): 210–26, doi : 10.1147/rd.62.0210, S2CID  19387286
49. Кахан, В. (20 мая 2001 г.), Алгоритмы псевдоделения для логарифмов и экспонент с плавающей запятой
50. Абрамовиц и Стегун, ред. 1972, с. 68
51. Сасаки, Т.; Канада, Ю. (1982), «Практически быстрая оценка log(x) с множественной точностью», Journal of Information Processing , 5 (4): 247–50 , получено 30 марта 2011 г.
52. Арендт, Тимм (1999), «Быстрые вычисления экспоненциальной функции», Stacs 99 , Конспекты лекций по информатике, том. 1564, Берлин, Нью-Йорк: Springer, стр. 302–12, номер документа : 10.1007/3-540-49116-3_28, ISBN. 978-3-540-65691-3
53. Хиллис, Дэнни (15 января 1989 г.), «Ричард Фейнман и машина соединений», Physics Today , 42 (2): 78, Бибкод : 1989PhT....42b..78H, doi : 10.1063/1.881196
54. Маор 2009, с. 135
55. Фрей, Брюс (2006), Взломы статистики, Серия хаков, Севастополь, Калифорния: О'Рейли , ISBN 978-0-596-10164-0, глава 6, раздел 64
56. Риккарди, Луиджи М. (1990), Лекции по прикладной математике и информатике, Манчестер: Manchester University Press, ISBN 978-0-7190-2671-3, п. 21, раздел 1.3.2
57. Бакши, Украина (2009), Телекоммуникационная инженерия, Пуна: Технические публикации, ISBN 978-81-8431-725-1^{[ постоянная мертвая ссылка ]} , раздел 5.2
58. Малинг, Джордж К. (2007), «Шум», Россинг, Томас Д. (редактор), Справочник по акустике Springer , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-30446-5, раздел 23.0.2
59. Ташев, Иван Желев (2009), Захват и обработка звука: практические подходы, Нью-Йорк: John Wiley & Sons , стр. 98, ISBN 978-0-470-31983-3
60. Чуи, К.К. (1997), Вейвлеты: математический инструмент для обработки сигналов, монографии SIAM по математическому моделированию и вычислениям, Филадельфия: Общество промышленной и прикладной математики , ISBN 978-0-89871-384-8
61. Краудер, Брюс; Эванс, Бенни; Ноэлл, Алан (2008), Функции и изменения: подход к моделированию студенческой алгебры (4-е изд.), Бостон: Cengage Learning, ISBN 978-0-547-15669-9, раздел 4.4.
62. Брэдт, Хейл (2004), Астрономические методы: физический подход к астрономическим наблюдениям , Кембриджская планетарная наука, Cambridge University Press , ISBN 978-0-521-53551-9, раздел 8.3, с. 231
63. Норби, Йенс (2000). «Происхождение и значение маленькой буквы p в pH». Тенденции биохимических наук . 25 (1): 36–37. дои : 10.1016/S0968-0004(99)01517-0. ПМИД  10637613.
64. IUPAC (1997), А. Д. Макнот, А. Уилкинсон (ред.), Сборник химической терминологии («Золотая книга») (2-е изд.), Оксфорд: Blackwell Scientific Publications, doi : 10.1351/goldbook , ISBN 978-0-9678550-9-7
65. Берд, Дж.О. (2001), Карманный справочник Newnes по инженерной математике (3-е изд.), Оксфорд: Newnes, ISBN 978-0-7506-4992-6, раздел 34
66. Гольдштейн, Э. Брюс (2009), Энциклопедия восприятия, Таузенд-Оукс, Калифорния: Sage, ISBN 978-1-4129-4081-8, стр. 355–56.
67. Мэтьюз, Джеральд (2000), Деятельность человека: познание, стресс и индивидуальные различия, Хоув: Psychology Press, ISBN 978-0-415-04406-6, п. 48
68. Велфорд, AT (1968), Основы мастерства , Лондон: Метуэн, ISBN 978-0-416-03000-6, OCLC  219156, п. 61
69. Пол М. Фиттс (июнь 1954 г.), «Информационная способность двигательной системы человека при контроле амплитуды движения», Журнал экспериментальной психологии , 47 (6): 381–91, doi : 10.1037/h0055392, PMID  13174710, S2CID  501599, перепечатано Полом М. Фиттсом (1992), «Информационная способность двигательной системы человека при контроле амплитуды движения» (PDF) , Journal of Experimental Psychology: General , 121 (3): 262–69, doi : 10.1037. /0096-3445.121.3.262, PMID  1402698 , получено 30 марта 2011 г.
70. Банерджи, JC (1994), Энциклопедический словарь психологических терминов, Нью-Дели: MD Publications, стр. 304, ISBN 978-81-85880-28-0, OCLC  33860167
71. Надель, Линн (2005), Энциклопедия когнитивных наук , Нью-Йорк: John Wiley & Sons , ISBN 978-0-470-01619-0, леммы Психофизика и восприятие: Обзор
72. Зиглер, Роберт С.; Опфер, Джон Э. (2003), «Развитие числовой оценки. Доказательства множественного представления числового количества» (PDF) , Psychoological Science , 14 (3): 237–43, CiteSeerX 10.1.1.727.3696 , doi : 10.1111 / 1467-9280.02438, PMID  12741747, S2CID  9583202, заархивировано из оригинала (PDF) 17 мая 2011 г. , получено 7 января 2011 г. 
73. Деэн, Станислас; Изар, Вероника; Спелке, Элизабет; Пика, Пьер (2008), «Логарифмический или линейный? Отличительные представления о числовой шкале в культурах коренных народов Западной и Амазонки», Science , 320 (5880): 1217–20, Бибкод : 2008Sci...320.1217D, CiteSeerX 10.1.1.362 .2390 , doi : 10.1126/science.1156540, PMC 2610411 , PMID  18511690  
74. Брейман, Лео (1992), Вероятность , Классика прикладной математики, Филадельфия: Общество промышленной и прикладной математики , ISBN 978-0-89871-296-4, раздел 12.9
75. Эйчисон, Дж.; Браун, JAC (1969), Логнормальное распределение , Cambridge University Press , ISBN 978-0-521-04011-2, OCLC  301100935
76. Жан Матье и Джулиан Скотт (2000), Введение в турбулентный поток, Cambridge University Press, стр. 50, ISBN 978-0-521-77538-0
77. Роуз, Колин; Смит, Мюррей Д. (2002), Математическая статистика с помощью Mathematica , Тексты Springer по статистике, Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-95234-5, раздел 11.3
78. Табачников, Серж (2005), Геометрия и бильярд , Провиденс, Род-Айленд: Американское математическое общество , стр. 36–40, ISBN 978-0-8218-3919-5, раздел 2.1
79. Дурчи, Синди; Хиллисон, Уильям; Пачини, Карл (2004), «Эффективное использование закона Бенфорда при обнаружении мошенничества в бухгалтерских данных» (PDF) , Journal of Forensic Accounting , V : 17–34, заархивировано из оригинала (PDF) 29 августа 2017 г. , получено 28 май 2018 г.
80. Вегенер, Инго (2005), Теория сложности: исследование пределов эффективных алгоритмов , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-21045-0, стр. 1–2
81. Харель, Дэвид; Фельдман, Ишай А. (2004), Алгоритмика: дух вычислений , Нью-Йорк: Аддисон-Уэсли , ISBN 978-0-321-11784-7, п. 143
82. Кнут, Дональд (1998), Искусство компьютерного программирования , Ридинг, Массачусетс: Аддисон-Уэсли, ISBN 978-0-201-89685-5, раздел 6.2.1, стр. 409–26.
83. Дональд Кнут 1998, раздел 5.2.4, стр. 158–68.
84. Вегенер, Инго (2005), Теория сложности: исследование пределов эффективных алгоритмов , Берлин, Нью-Йорк: Springer-Verlag , стр. 20, ISBN 978-3-540-21045-0
85. Мор, Ганс; Шопфер, Питер (1995), Физиология растений , Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-3-540-58016-4, глава 19, с. 298
86. Эко, Умберто (1989), Открытая работа , издательство Гарвардского университета , ISBN 978-0-674-63976-8, раздел III.I
87. Спротт, Жюльен Клинтон (2010), «Элегантный хаос: алгебраически простые хаотические потоки», Элегантный хаос: алгебраически простые хаотические потоки. Под редакцией Спротта Жюльена Клинтона. Опубликовано World Scientific Publishing Co. Pte. Ltd , Нью-Джерси: World Scientific , Bibcode : 2010ecas.book.....S, doi : 10.1142/7183, ISBN 978-981-283-881-0, раздел 1.9
88. Хельмберг, Гилберт (2007), Знакомство с фракталами , Учебник Де Грюйтера, Берлин, Нью-Йорк: Вальтер де Грюйтер, ISBN 978-3-11-019092-2
89. Райт, Дэвид (2009), Математика и музыка , Провиденс, Род-Айленд: Книжный магазин AMS, ISBN 978-0-8218-4873-9, глава 5
90. Бейтман, ПТ; Даймонд, Гарольд Г. (2004), Аналитическая теория чисел: вводный курс , Нью-Джерси: World Scientific , ISBN 978-981-256-080-3, OCLC  492669517, теорема 4.1
91. PT Bateman & Diamond 2004, Теорема 8.15.
92. Сломсон, Алан Б. (1991), Введение в комбинаторику , Лондон: CRC Press , ISBN 978-0-412-35370-3, Глава 4
93. Гангули, С. (2005), Элементы комплексного анализа , Калькутта: Academic Publishers, ISBN 978-81-87504-86-3, Определение 1.6.3
94. Неванлинна, Рольф Герман ; Паатеро, Вейкко (2007), «Введение в комплексный анализ», Лондон: Хильгер , Провиденс, Род-Айленд: Книжный магазин AMS, Bibcode : 1974aitc.book.....W, ISBN 978-0-8218-4399-4, раздел 5.9
95. Мур, Терал Орвис; Хэдлок, Эдвин Х. (1991), Комплексный анализ , Сингапур: World Scientific , ISBN 978-981-02-0246-0, раздел 1.2
96. Уайльд, Иван Фрэнсис (2006), Конспекты лекций по комплексному анализу, Лондон: Imperial College Press, ISBN 978-1-86094-642-4, теорема 6.1.
97. Хайэм, Николас (2008), Функции матриц. Теория и вычисления , Филадельфия, Пенсильвания: SIAM , ISBN 978-0-89871-646-7, глава 11.
98. Нойкирх, Юрген (1999), Algebraische Zahlentheorie , Grundlehren der mathematischen Wissenschaften , vol. 322, Берлин: Springer-Verlag , ISBN 978-3-540-65399-8, МР  1697859, Збл  0956.11021, раздел II.5.
99. Хэнкок, Эдвин Р.; Мартин, Ральф Р.; Сабин, Малкольм А. (2009), Математика поверхностей XIII: 13-я Международная конференция IMA, Йорк, Великобритания, 7–9 сентября 2009 г., Материалы, Springer, стр. 379, ISBN 978-3-642-03595-1
100. Стинсон, Дуглас Роберт (2006), Криптография: теория и практика (3-е изд.), Лондон: CRC Press , ISBN 978-1-58488-508-5
101. Лидл, Рудольф; Нидеррайтер, Харальд (1997), Конечные поля , издательство Кембриджского университета, ISBN 978-0-521-39231-0
102. Корлесс, Р.; Гонне, Г.; Заяц, Д.; Джеффри, Д.; Кнут, Дональд (1996), «О функции Ламберта W» (PDF) , Advance in Computational Mathematics , 5 : 329–59, doi : 10.1007/BF02124750, ISSN  1019-7168, S2CID  29028411, заархивировано из оригинала (PDF) 14 декабря 2010 г. , дата обращения 13 февраля 2011 г.
103. Черкасский, Владимир; Черкасский Владимир С.; Мюльер, Филип (2007), Обучение на данных: концепции, теория и методы , Серия Wiley об адаптивных и обучающих системах для обработки сигналов, связи и управления, Нью-Йорк: John Wiley & Sons , ISBN 978-0-471-68182-3, п. 357
104. Бурбаки, Николя (1998), Общая топология. Главы 5–10 , Элементы математики, Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-64563-4, МР  1726872, раздел V.4.1
105. Амбарцумян, Р.В. (1990), Факторизационное исчисление и геометрическая вероятность , Cambridge University Press , ISBN 978-0-521-34535-4, раздел 1.4
106. Эно, Элен; Фивег, Эккарт (1992), Лекции по теоремам об исчезновении , Семинар DMV, том. 20, Базель, Бостон: Birkhäuser Verlag, CiteSeerX 10.1.1.178.3227 , doi : 10.1007/978-3-0348-8600-0, ISBN  978-3-7643-2822-1, МР  1193913, раздел 2
107. Апостол, TM (2010), «Логарифм», в Олвере, Фрэнк У.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN 978-0-521-19225-5, МР  2723248.

Внешние ссылки

• СМИ, связанные с логарифмом, на Викискладе?
• Словарное определение логарифма в Викисловаре
• Урок по логарифмам можно найти в Викиверситете.
• Вайсштейн, Эрик В. , «Логарифм», MathWorld.
• Академия Хана: Логарифмы, бесплатные микролекции онлайн
• «Логарифмическая функция», Математическая энциклопедия , EMS Press , 2001 [1994]
• Колин Байфлит, Обучающее видео по логарифмам , получено 12 октября 2010 г.
• Эдвард Райт, Перевод работы Нэпьера по логарифмам, заархивировано из оригинала 3 декабря 2002 г. , получено 12 октября 2010 г.{{citation}}: CS1 maint: unfit URL (link)
• Глейшер, Джеймс Уитбред Ли (1911), «Логарифм»  , в Чисхолме, Хью (редактор), Британская энциклопедия , том. 16 (11-е изд.), Cambridge University Press, стр. 868–77.