Алгебраическая кривая

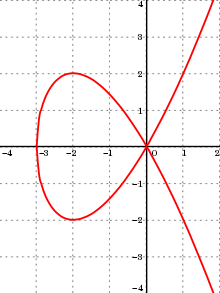
В математике аффинная алгебраическая плоская кривая — это нулевое множество многочлена от двух переменных. Проективная алгебраическая плоская кривая — это нулевое множество в проективной плоскости однородного многочлена от трех переменных. Аффинная алгебраическая плоская кривая может быть дополнена в проективную алгебраическую плоскую кривую путем гомогенизации ее определяющего многочлена. Наоборот, проективная алгебраическая плоская кривая однородного уравнения $h$ $($ $x$ $,$ $y$ $,$ $t$ $) = 0$ может быть ограничена аффинной алгебраической плоской кривой уравнения $h$ $($ $x$ $,$ $y$ $, 1) = 0$ . Эти две операции являются обратными друг другу; поэтому фраза алгебраическая плоская кривая часто используется без явного указания того, рассматривается ли аффинный или проективный случай.

Если определяющий многочлен плоской алгебраической кривой неприводим , то мы имеем неприводимую плоскую алгебраическую кривую . В противном случае алгебраическая кривая является объединением одной или нескольких неприводимых кривых, называемых ее компонентами , которые определяются неприводимыми множителями.

В более общем смысле, алгебраическая кривая — это алгебраическое многообразие размерности один . (В некоторых контекстах алгебраическое множество размерности один также называется алгебраической кривой, но в этой статье это не будет так.) Эквивалентно, алгебраическая кривая — это алгебраическое многообразие, которое бирационально эквивалентно неприводимой алгебраической плоской кривой. Если кривая содержится в аффинном пространстве или проективном пространстве , можно взять проекцию для такой бирациональной эквивалентности.

Эти бирациональные эквивалентности сводят большую часть изучения алгебраических кривых к изучению алгебраических плоских кривых. Однако некоторые свойства не сохраняются при бирациональной эквивалентности и должны изучаться на неплоских кривых. Это, в частности, касается степени и гладкости . Например, существуют гладкие кривые рода 0 и степени больше двух, но любая плоская проекция таких кривых имеет особые точки (см. Формула род–степень ).

Неплоскую кривую часто называют пространственной кривой или косой кривой .

В евклидовой геометрии

Алгебраическая кривая на евклидовой плоскости — это множество точек, координаты которых являются решениями двумерного полиномиального уравнения p ( x , y ) = 0. Это уравнение часто называют неявным уравнением кривой, в отличие от кривых, которые являются графиком функции, явно определяющей y как функцию x .

С кривой, заданной таким неявным уравнением, первыми проблемами являются определение формы кривой и ее рисование. Эти проблемы не так легко решить, как в случае графика функции, для которой y может быть легко вычислено для различных значений x . Тот факт, что определяющее уравнение является полиномом, подразумевает, что кривая имеет некоторые структурные свойства, которые могут помочь в решении этих проблем.

Каждая алгебраическая кривая может быть однозначно разложена на конечное число гладких монотонных дуг (также называемых ветвями ), иногда соединенных некоторыми точками, иногда называемыми «замечательными точками», и, возможно, конечное число изолированных точек, называемых acnodes . Гладкая монотонная дуга — это график гладкой функции , которая определена и монотонна на открытом интервале оси x . В каждом направлении дуга либо неограничена (обычно называется бесконечной дугой ), либо имеет конечную точку, которая является либо особой точкой (это будет определено ниже), либо точкой с касательной, параллельной одной из осей координат.

Например, для кубики Чирнхаузена есть две бесконечные дуги, имеющие начало (0,0) в качестве конечной точки. Эта точка является единственной особой точкой кривой. Есть также две дуги, имеющие эту особую точку в качестве одной конечной точки и имеющие вторую конечную точку с горизонтальной касательной. Наконец, есть две другие дуги, каждая из которых имеет одну из этих точек с горизонтальной касательной в качестве первой конечной точки и имеющую единственную точку с вертикальной касательной в качестве второй конечной точки. Напротив, синусоида, безусловно , не является алгебраической кривой, имея бесконечное число монотонных дуг.

Чтобы нарисовать алгебраическую кривую, важно знать замечательные точки и их касательные, бесконечные ветви и их асимптоты (если таковые имеются) и способ, которым дуги их соединяют. Также полезно рассматривать точки перегиба как замечательные точки. Когда вся эта информация нарисована на листе бумаги, форма кривой обычно выглядит довольно ясно. Если нет, достаточно добавить несколько других точек и их касательных, чтобы получить хорошее описание кривой.

Методы вычисления замечательных точек и их касательных описаны ниже в разделе Замечательные точки плоской кривой.

Плоские проективные кривые

Часто желательно рассматривать кривые в проективном пространстве . Алгебраическая кривая в проективной плоскости или плоская проективная кривая — это множество точек в проективной плоскости, проективные координаты которых являются нулями однородного многочлена от трех переменных P ( x , y , z ).

Каждая аффинная алгебраическая кривая уравнения p ( x , y ) = 0 может быть дополнена в проективную кривую уравнения , где — результат гомогенизации p . Обратно, если P ( x , y , z ) = 0 — однородное уравнение проективной кривой, то P ( x , y , 1) = 0 — уравнение аффинной кривой, состоящей из точек проективной кривой, третья проективная координата которых не равна нулю. Эти две операции взаимно обратны друг другу, так как и, если p определяется как , то как только однородный многочлен P не делится на z . $^{h}p(x,y,z)=0,$ $^{h}p(x,y,z)=z^{\deg(p)}p\left({\frac {x}{z}},{\frac {y}{z}}\right)$ $^{h}p(x,y,1)=p(x,y)$ ${\ displaystyle p (x, y) = P (x, y, 1)}$ ${\ displaystyle ^ {h} p (x, y, z) = P (x, y, z),}$

Например, проективная кривая уравнения x ² + y ² − z ² является проективным завершением единичной окружности уравнения x ² + y ² − 1 = 0.

Это подразумевает, что аффинная кривая и ее проективное завершение являются одними и теми же кривыми, или, точнее, что аффинная кривая является частью проективной кривой, которая достаточно велика, чтобы хорошо определить «полную» кривую. Эта точка зрения обычно выражается, называя «точками на бесконечности» аффинной кривой точки (в конечном числе) проективного завершения, которые не принадлежат аффинной части.

Проективные кривые часто изучаются сами по себе. Они также полезны для изучения аффинных кривых. Например, если p ( x , y ) — многочлен, определяющий аффинную кривую, то помимо частных производных и полезно рассмотреть производную на бесконечности $p'_{x}$ $p'_{y}$ ${\ displaystyle p'_ {\ infty } (x, y) = {^ {h} p'_ {z} (x, y, 1)}.}$

Например, уравнение касательной аффинной кривой уравнения p ( x , y ) = 0 в точке ( a , b ) имеет вид $xp'_{x}(a,b)+yp'_{y}(a,b)+p'_{\infty }(a,b)=0.$

Замечательные точки плоской кривой

В этом разделе мы рассмотрим плоскую алгебраическую кривую , определяемую двумерным многочленом p ( x , y ), и ее проективное пополнение, определяемое гомогенизацией p . $P(x,y,z)={}^{h}p(x,y,z)$

Пересечение с линией

Знание точек пересечения кривой с заданной прямой часто бывает полезным. Пересечение с осями координат и асимптотами полезно для построения кривой. Пересечение с прямой, параллельной осям, позволяет найти по крайней мере одну точку в каждой ветви кривой. Если доступен эффективный алгоритм поиска корня , это позволяет построить кривую, построив точку пересечения со всеми прямыми, параллельными оси y и проходящими через каждый пиксель на оси x .

Если многочлен, определяющий кривую, имеет степень d , любая линия пересекает кривую не более чем в d точках. Теорема Безу утверждает, что это число равно в точности d , если точки ищутся в проективной плоскости над алгебраически замкнутым полем (например, комплексными числами ) и подсчитываются с их кратностью . Метод вычисления, который следует ниже, снова доказывает эту теорему в этом простом случае.

Чтобы вычислить пересечение кривой, заданной полиномом p, с линией уравнения ax + by + c = 0, решается уравнение линии относительно x (или для y , если a = 0). Подставляя результат в p , получается уравнение одной переменной q ( y ) = 0 (или q ( x ) = 0, если уравнение линии было решено относительно y ), каждый из корней которого является одной координатой точки пересечения. Другая координата выводится из уравнения линии. Кратность точки пересечения равна кратности соответствующего корня. Точка пересечения существует на бесконечности, если степень q меньше степени p ; кратность такой точки пересечения на бесконечности равна разности степеней p и q .

Касательная в точке

Касательная в точке ( a , b ) кривой является линией уравнения , как и для каждой дифференцируемой кривой, определяемой неявным уравнением. В случае полиномов другая формула для касательной имеет более простой постоянный член и является более симметричной: $(xa)p'_{x}(a,b)+(yb)p'_{y}(a,b)=0$

$xp'_{x}(a,b)+yp'_{y}(a,b)+p'_{\infty }(a,b)=0,$

где — производная на бесконечности. Эквивалентность двух уравнений следует из теоремы Эйлера об однородной функции, примененной к P. $p'_ {\infty }(x,y)=P'_{z}(x,y,1)$

Если касательная не определена и точка является особой точкой . $p'_{x}(a,b)=p'_{y}(a,b)=0,$

Это немедленно распространяется на проективный случай: уравнение касательной в точке с проективными координатами ( a : b : c ) проективной кривой уравнения P ( x , y , z )=0 имеет вид

$xP'_{x}(a,b,c)+yP'_{y}(a,b,c)+zP'_{z}(a,b,c)=0,$

а точки кривых, которые являются особыми, — это точки, такие, что

$P'_{x}(a,b,c)=P'_{y}(a,b,c)=P'_{z}(a,b,c)=0.$

(Условие P ( a , b , c ) = 0 вытекает из этих условий, из теоремы Эйлера об однородной функции.)

Асимптоты

Каждая бесконечная ветвь алгебраической кривой соответствует точке на бесконечности на кривой, то есть точке проективного завершения кривой, которая не принадлежит ее аффинной части. Соответствующая асимптота является касательной к кривой в этой точке. Общая формула для касательной к проективной кривой может применяться, но в этом случае стоит сделать ее явной.

Пусть — разложение многочлена, определяющего кривую, на его однородные части, где p _i — сумма одночленов p степени i . Отсюда следует, что и $p=p_{d}+\cdots +p_{0}$ $P={^{h}p}=p_{d}+zp_{d-1}+\cdots +z^{d}p_{0}$ $P'_{z}(a,b,0)=p_{d-1}(a,b).$

Точка на бесконечности кривой является нулем p вида ( a , b , 0). Эквивалентно, ( a , b ) является нулем p _d . Основная теорема алгебры подразумевает, что над алгебраически замкнутым полем (обычно полем комплексных чисел) p _d разлагается на произведение линейных множителей. Каждый множитель определяет точку на бесконечности на кривой: если bx − ay является таким множителем, то он определяет точку на бесконечности ( a , b , 0). Над действительными числами p _d разлагается на линейные и квадратичные множители. Неприводимые квадратичные множители определяют недействительные точки на бесконечности, а действительные точки задаются линейными множителями. Если ( a , b , 0) является точкой на бесконечности кривой, говорят, что ( a , b ) является асимптотическим направлением . Принимая q = p _{d ,} уравнение соответствующей асимптоты имеет вид $xq'_{x}(a,b)+yq'_{y}(a,b)+p_{d-1}(a,b)=0.$

Если и асимптота — это прямая на бесконечности, и, в действительном случае, кривая имеет ветвь, похожую на параболу . В этом случае говорят, что кривая имеет параболическую ветвь . Если кривая имеет особую точку на бесконечности и может иметь несколько асимптот. Их можно вычислить методом вычисления касательного конуса особой точки. $q'_{x}(a,b)=q'_{y}(a,b)=0$ $p_{d-1}(a,b)\neq 0,$ $q'_{x}(a,b)=q'_{y}(a,b)=p_{d-1}(a,b)=0,$

Особые точки

Особые точки кривой степени d, определяемые полиномом p ( x , y ) степени d , являются решениями системы уравнений: В нулевой характеристике эта система эквивалентна , где с обозначениями предыдущего раздела Системы эквивалентны в силу теоремы Эйлера об однородной функции . Последняя система имеет то преимущество, что имеет третий полином степени d -1 вместо d . $p'_{x}(x,y)=p'_{y}(x,y)=p(x,y)=0.$ $p'_{x}(x,y)=p'_{y}(x,y)=p'_{\infty }(x,y)=0,$ $p'_{\infty }(x,y)=P'_{z}(x,y,1).$

Аналогично, для проективной кривой, заданной однородным многочленом P ( x , y , z ) степени d , особые точки имеют решения системы в виде однородных координат . (В положительной характеристике уравнение должно быть добавлено к системе.) $P'_{x}(x,y,z)=P'_{y}(x,y,z)=P'_{z}(x,y,z)=0$ $P(x,y,z)$

Это подразумевает, что число особых точек конечно, пока p ( x , y ) или P ( x , y , z ) не содержит квадратов . Таким образом, теорема Безу подразумевает, что число особых точек не превышает ( d − 1) ² , но эта граница не является точной, поскольку система уравнений переопределена . Если допускаются приводимые многочлены , точная граница равна d ( d − 1)/2, это значение достигается, когда многочлен разлагается на линейные множители, то есть если кривая является объединением d прямых. Для неприводимых кривых и многочленов число особых точек не превышает ( d − 1)( d − 2)/2 из-за формулы, выражающей род через особенности (см. ниже). Максимума достигают кривые рода нуль, все особенности которых имеют кратность два и различные касательные (см. ниже).

Уравнение касательных в особой точке задается ненулевой однородной частью низшей степени в ряде Тейлора многочлена в особой точке. Если изменить координаты так, чтобы поместить особую точку в начало координат, то уравнение касательных в особой точке будет ненулевой однородной частью низшей степени многочлена, а кратность особой точки будет степенью этой однородной части.

Аналитическая структура

Изучение аналитической структуры алгебраической кривой в окрестности особой точки дает точную информацию о топологии особенностей. Фактически, вблизи особой точки действительная алгебраическая кривая представляет собой объединение конечного числа ветвей, которые пересекаются только в особой точке и выглядят либо как точка возврата , либо как гладкая кривая.

Вблизи регулярной точки одна из координат кривой может быть выражена как аналитическая функция другой координаты. Это является следствием теоремы об аналитической неявной функции и подразумевает, что кривая является гладкой вблизи точки. Вблизи особой точки ситуация более сложная и включает ряды Пюизо , которые обеспечивают аналитические параметрические уравнения ветвей.

Для описания сингулярности стоит перевести кривую так, чтобы сингулярность находилась в начале координат. Это состоит в замене переменной вида где - координаты особой точки. В дальнейшем рассматриваемая сингулярная точка всегда предполагается в начале координат. $X=x-a,Y=y-b,$ $a,b$

Уравнение алгебраической кривой имеет вид где $f$ — многочлен от $x$ и $y$ . Этот многочлен можно рассматривать как многочлен от $y$ с коэффициентами в алгебраически замкнутом поле ряда Пюизе от $x$ . Таким образом, $f$ можно разложить на множители вида где $P$ — ряд Пюизе. Все эти множители различны, если $f$ — неприводимый многочлен , поскольку это подразумевает, что $f$ является свободным от квадратов , свойство, которое не зависит от поля коэффициентов. $f(x,y)=0,$ $y-P(x),$

Ряды Пюизё, которые здесь встречаются, имеют вид , где $d$ — положительное целое число, а ⁠ ⁠ — целое число, которое также можно считать положительным, поскольку мы рассматриваем только ветви кривой, проходящие через начало координат. Без потери общности можно предположить, что $d$ является взаимно простым с наибольшим общим делителем n $таким$ , что ⁠ ⁠ (в противном случае можно было бы выбрать меньший общий знаменатель для показателей степеней). $P(x)=\sum _{n=n_{0}}^{\infty }a_{n}x^{n/d},$ $n_{0}$ $a_{n}\neq 0$

Пусть ⁠ ⁠ $\omega _{d}$ будет примитивным корнем $d-$ й степени из единицы . Если указанный выше ряд Пюизё встречается в факторизации ⁠ ⁠ $f(x,y)=0$ , то ряд $d$ также встречается в факторизации (следствие теории Галуа ). Эти ряды $d$ называются сопряженными и рассматриваются как одна ветвь кривой с индексом ветвления $d$ . $P_{i}(x)=\sum _{n=n_{0}}^{\infty }a_{n}\omega _{d}^{i}x^{n/d}$

В случае действительной кривой, то есть кривой, заданной полиномом с действительными коэффициентами, могут возникнуть три случая. Если ни один ⁠ ⁠ $P_{i}(x)$ не имеет действительных коэффициентов, то имеет место недействительная ветвь. Если какой-то ⁠ ⁠ $P_{i}(x)$ имеет действительные коэффициенты, то можно выбрать его в качестве ⁠ ⁠ $P_{0}(x)$ . Если $d$ нечетно, то каждое действительное значение $x$ дает действительное значение ⁠ ⁠ $P_{0}(x)$ , и у нас есть действительная ветвь, которая выглядит регулярной, хотя она является сингулярной, если $d > 1$ . Если $d$ четно, то ⁠ ⁠ $P_{0}(x)$ и ⁠ ⁠ $P_{d/2}(x)$ имеют действительные значения, но только для $x \geq 0$ . В этом случае действительная ветвь выглядит как касп (или является каспом, в зависимости от определения каспа, которое используется).

Например, обычный касп имеет только одну ветвь. Если он определяется уравнением , то факторизация имеет индекс ветвления 2, и два множителя являются действительными и определяют каждый половину ветви. Если касп вращается, его уравнение становится и факторизация имеет вид с (коэффициент ⁠ ⁠ не был упрощен до $j$ для того, чтобы показать, как специализировано приведенное выше определение ⁠ ⁠ ). Здесь индекс ветвления равен 3, и только один множитель является действительным; это показывает, что в первом случае два множителя следует рассматривать как определяющие одну и ту же ветвь. $y^{2}-x^{3}=0,$ $(y-x^{3/2})(y+x^{3/2});$ $y^{3}-x^{2}=0,$ $(y-x^{2/3})(y-j^{2}x^{2/3})(y-(j^{2})^{2}x^{2/3}),$ $j=(1+{\sqrt {-3}})/2$ $(j^{2})^{2}$ $P_{i}(x)$

Неплоские алгебраические кривые

Алгебраическая кривая — это алгебраическое многообразие размерности один . Это подразумевает, что аффинная кривая в аффинном пространстве размерности n определяется, по крайней мере, n − 1 полиномами от n переменных. Чтобы определить кривую, эти полиномы должны генерировать простой идеал размерности Крулля 1. Это условие нелегко проверить на практике. Поэтому может быть предпочтителен следующий способ представления неплоских кривых.

Пусть будут n полиномов от двух переменных x ₁ и x _2, таких, что f неприводима. Точки в аффинном пространстве размерности n, такие, координаты которых удовлетворяют уравнениям и неравенствам $f,g_{0},g_{3},\ldots ,g_{n}$

${\begin{aligned}&f(x_{1},x_{2})=0\\&g_{0}(x_{1},x_{2})\neq 0\\x_{3}&={\frac {g_{3}(x_{1},x_{2})}{g_{0}(x_{1},x_{2})}}\\&{}\ \vdots \\x_{n}&={\frac {g_{n}(x_{1},x_{2})}{g_{0}(x_{1},x_{2})}}\end{aligned}}$

являются всеми точками алгебраической кривой, в которой удалено конечное число точек. Эта кривая определяется системой генераторов идеала многочленов h, таких что существует целое число k, такое, что принадлежит идеалу, порожденному . Это представление является бирациональной эквивалентностью между кривой и плоской кривой, определенной f . Каждая алгебраическая кривая может быть представлена таким образом. Однако может потребоваться линейная замена переменных, чтобы сделать почти всегда инъективной проекцию на две первые переменные. Когда требуется замена переменных, почти каждое изменение удобно, как только оно определено над бесконечным полем. $g_{0}^{k}h$ $f,x_{3}g_{0}-g_{3},\ldots ,x_{n}g_{0}-g_{n}$

Это представление позволяет нам легко вывести любое свойство неплоской алгебраической кривой, включая ее графическое представление, из соответствующего свойства ее плоской проекции.

Для кривой, заданной ее неявными уравнениями, приведенное выше представление кривой может быть легко выведено из базиса Грёбнера для блочного упорядочения, такого что блок меньших переменных равен ( x ₁ , x ₂ ). Многочлен f является единственным многочленом в базе, который зависит только от x ₁ и x ₂ . Дроби g _i / g ₀ получаются путем выбора для i = 3, ..., n многочлена в базе, который линейен по x _i и зависит только от x ₁ , x ₂ и x _i . Если эти варианты невозможны, это означает, что либо уравнения определяют алгебраическое множество , которое не является многообразием, либо многообразие не имеет размерности один, либо необходимо изменить координаты. Последний случай имеет место, когда f существует и является единственным, и для i = 3, ..., n существуют многочлены, старший моном которых зависит только от x ₁ , x ₂ и x _i .

Поля алгебраических функций

Изучение алгебраических кривых можно свести к изучению неприводимых алгебраических кривых: тех кривых, которые не могут быть записаны как объединение двух меньших кривых. С точностью до бирациональной эквивалентности неприводимые кривые над полем F категорически эквивалентны полям алгебраических функций от одной переменной над F . Такое поле алгебраических функций является расширением поля K поля F , содержащим элемент x , который трансцендентен над F , и таким, что K является конечным алгебраическим расширением F ( x ), которое является полем рациональных функций от неопределенного x над F .

Например, рассмотрим поле C комплексных чисел, над которым мы можем определить поле C ( x ) рациональных функций в C . Если $y 2 = x 3 - x - 1$ , то поле C ( x , y ) является полем эллиптических функций . Элемент x не определен однозначно; поле также можно рассматривать, например, как расширение C ( y ). Алгебраическая кривая, соответствующая полю функций, — это просто множество точек ( x , y ) в C ^{2 ,} удовлетворяющих $y 2 = x 3 - x - 1$ .

Если поле F не является алгебраически замкнутым, точка зрения на функциональные поля немного более общая, чем точка зрения на рассмотрение геометрического места точек, поскольку мы включаем, например, «кривые» без точек на них. Например, если базовое поле F является полем R действительных чисел, то $x 2 + y 2 = -1$ определяет алгебраическое поле расширения R ( x ), но соответствующая кривая, рассматриваемая как подмножество R ^{2 ,} не имеет точек. Уравнение $x 2 + y 2 = -1$ действительно определяет неприводимую алгебраическую кривую над R в схемном смысле ( целая , разделенная одномерная схема конечного типа над R ). В этом смысле взаимно однозначное соответствие между неприводимыми алгебраическими кривыми над F (с точностью до бирациональной эквивалентности) и алгебраическими функциональными полями от одной переменной над F выполняется в общем случае.

Две кривые могут быть бирационально эквивалентны (т.е. иметь изоморфные поля функций), не будучи изоморфными как кривые. Ситуация упрощается, когда имеешь дело с неособыми кривыми, т.е. с теми, у которых нет никаких особенностей. Две неособые проективные кривые над полем изоморфны тогда и только тогда, когда их поля функций изоморфны.

Теорема Тзена касается поля функций алгебраической кривой над алгебраически замкнутым полем.

Сложные кривые и реальные поверхности

Комплексная проективная алгебраическая кривая находится в n -мерном комплексном проективном пространстве CP ⁿ . Она имеет комплексную размерность n , но топологическую размерность, как вещественное многообразие , 2 n , и является компактной , связной и ориентируемой . Алгебраическая кривая над C также имеет топологическую размерность два; другими словами, это поверхность .

Топологический род этой поверхности, то есть число ручек или дырок от бублика, равен геометрическому роду алгебраической кривой, который может быть вычислен алгебраическими средствами. Короче говоря, если рассмотреть плоскую проекцию неособой кривой, которая имеет степень d и только обычные особенности (особенности кратности два с различными касательными), то род равен $(d - 1)(d - 2)/2 - k$ , где k — число этих особенностей.

Компактные римановы поверхности

Риманова поверхность — связное комплексное аналитическое многообразие одного комплексного измерения, что делает ее связным вещественным многообразием двух измерений. Она компактна , если она компактна как топологическое пространство.

Существует тройная эквивалентность категорий между категорией гладких неприводимых проективных алгебраических кривых над C (с непостоянными регулярными отображениями в качестве морфизмов), категорией компактных римановых поверхностей (с непостоянными голоморфными отображениями в качестве морфизмов) и противоположностью категории алгебраических функциональных полей от одной переменной над C (с гомоморфизмами полей, фиксирующими C в качестве морфизмов). Это означает, что при изучении этих трех предметов мы в некотором смысле изучаем одно и то же. Это позволяет использовать комплексные аналитические методы в алгебраической геометрии, а алгебро-геометрические методы в комплексном анализе и методы теории поля в обоих случаях. Это характерно для гораздо более широкого класса задач в алгебраической геометрии.

Более общую теорию см. также в разделах алгебраическая геометрия и аналитическая геометрия .

Сингулярности

Используя внутреннюю концепцию касательного пространства , точки P на алгебраической кривой C классифицируются как гладкие (синоним: неособые ), или же особые . При наличии n − 1 однородных многочленов от n + 1 переменных мы можем найти матрицу Якоби как матрицу ( n − 1)×( n + 1) частных производных. Если ранг этой матрицы равен n − 1, то многочлены определяют алгебраическую кривую (в противном случае они определяют алгебраическое многообразие более высокой размерности). Если ранг остается n − 1, когда матрица Якоби вычисляется в точке P на кривой, то точка является гладкой или регулярной точкой; в противном случае это особая точка . В частности, если кривая является плоской проективной алгебраической кривой, определяемой одним однородным полиномиальным уравнением f ( x , y , z ) = 0, то особые точки — это в точности точки P , в которых ранг матрицы 1×( n + 1) равен нулю, то есть, где ${\frac {\partial f}{\partial x}}(P)={\frac {\partial f}{\partial y}}(P)={\frac {\partial f}{\partial z}}(P)=0.$

Поскольку f — многочлен, это определение является чисто алгебраическим и не делает никаких предположений о природе поля F , которое, в частности, не обязательно должно быть действительными или комплексными числами. Конечно, следует напомнить, что (0,0,0) не является точкой кривой и, следовательно, не является особой точкой.

Аналогично, для аффинной алгебраической кривой, заданной одним полиномиальным уравнением f ( x , y ) = 0, особые точки — это в точности точки P кривой , где ранг матрицы Якоби размером 1× n равен нулю, то есть где

$f(P)={\frac {\partial f}{\partial x}}(P)={\frac {\partial f}{\partial y}}(P)=0.$

Сингулярности кривой не являются бирациональными инвариантами. Однако, обнаружение и классификация сингулярностей кривой является одним из способов вычисления рода , который является бирациональным инвариантом. Чтобы это работало, мы должны рассматривать кривую проективно и требовать, чтобы F была алгебраически замкнута, так что все сингулярности, которые принадлежат кривой, рассматриваются.

Классификация особенностей

К особым точкам относятся множественные точки, в которых кривая пересекает саму себя, а также различные типы точек возврата , например, те, которые показаны кривой с уравнением x ³ = y ² в точке (0,0).

Кривая C имеет не более конечного числа особых точек. Если у нее нет ни одной, ее можно назвать гладкой или неособой . Обычно это определение понимается над алгебраически замкнутым полем и для кривой C в проективном пространстве (т.е. полном в смысле алгебраической геометрии). Например, плоская кривая уравнения считается особой, как имеющая особую точку (касп) на бесконечности. $y-x^{3}=0$

В оставшейся части этого раздела рассматривается плоская кривая $C,$ определяемая как нулевое множество двумерного полинома $f (x, y)$ . Некоторые результаты, но не все, могут быть обобщены на неплоские кривые.

Особые точки классифицируются с помощью нескольких инвариантов. Кратность $m$ определяется как максимальное целое число, такое, что производные $f$ до всех порядков до $m - 1$ обращаются в нуль (также минимальное число пересечений между кривой и прямой в точке $P$ ). Интуитивно особая точка имеетдельта-инвариант $δ,$ если он концентрирует $δ$ обычных двойных точек в $P.$ Чтобы сделать это точным,раздутияпроизводит так называемыебесконечно близкие точки, и суммирование $m (m - 1)/2$ по бесконечно близким точкам, гдеm— их кратность, производит $δ$ . Для неприводимой и приведенной кривой и точки $P$ мы можем определить $δ$ алгебраически как длину,где— локальное кольцо вP, а— его интегральное замыкание.^[1] ${\widetilde {\mathcal {O}}}_{P}/{\mathcal {O}}_{P}$ ${\mathcal {O}}_{P}$ ${\widetilde {\mathcal {O}}}_{P}$

Число Милнора $μ$ особенности — это степень отображения $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠градиент f ( x , y )/|град f ( x , y )|⁠$ на малой сфере радиуса ε, в смысле топологической степени непрерывного отображения , где $grad f$ — (комплексное) градиентное векторное поле f . Оно связано с δ и r формулой Милнора–Юнга,

μ = 2δ − r + 1.

Здесь число ветвлений r для P — это число локально неприводимых ветвей в P. Например, r = 1 в обычном каспе и r = 2 в обычной двойной точке. Кратность m не меньше r , и P является сингулярным тогда и только тогда, когда m не меньше 2. Более того, δ не меньше m ( m -1)/2.

Вычисление дельта-инвариантов всех особенностей позволяет определить род g кривой; если d — степень, то

$g={\frac {1}{2}}(d-1)(d-2)-\sum _{P}\delta _{P},$

где сумма берется по всем особым точкам P комплексной проективной плоской кривой. Она называется формулой рода .

Присвоим инварианты [ m , δ, r ] сингулярности, где m — кратность, δ — дельта-инвариант, а r — число ветвления. Тогда обычный касп — это точка с инвариантами [2,1,1], а обычная двойная точка — это точка с инвариантами [2,1,2], а обычная m -кратная точка — это точка с инвариантами [ m , m ( m − 1)/2, m ].

Примеры кривых

Рациональные кривые

Рациональная кривая , также называемая уникурсальной кривой, — это любая кривая, которая бирационально эквивалентна прямой, которую мы можем считать проективной прямой; соответственно, мы можем отождествить функциональное поле кривой с полем рациональных функций от одной неопределенной F ( x ). Если F алгебраически замкнута, это эквивалентно кривой рода нуль; однако поле всех действительных алгебраических функций, определенных на действительном алгебраическом многообразии x ² + y ² = −1, является полем рода нуль, которое не является полем рациональных функций.

Конкретно, рациональная кривая, вложенная в аффинное пространство размерности n над F, может быть параметризована (за исключением изолированных исключительных точек) посредством n рациональных функций одного параметра t ; путем приведения этих рациональных функций к одному и тому же знаменателю, n +1 результирующих многочленов определяют полиномиальную параметризацию проективного завершения кривой в проективном пространстве. Примером является рациональная нормальная кривая , где все эти многочлены являются мономами .

Любое коническое сечение, определенное над F с рациональной точкой в F, является рациональной кривой. Его можно параметризовать, проведя линию с наклоном t через рациональную точку и пересечение с плоской квадратичной кривой; это дает многочлен с F -рациональными коэффициентами и одним F -рациональным корнем, следовательно, другой корень также является F -рациональным (т. е. принадлежит F ).

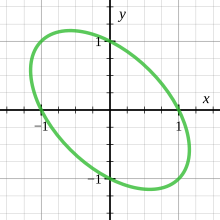
Например, рассмотрим эллипс x ² + xy + y ² = 1, где (−1, 0) — рациональная точка. Проводя линию с наклоном t из (−1, 0), y = t ( x + 1), подставляя ее в уравнение эллипса, разлагая на множители и решая относительно x , получаем

$x={\frac {1-t^{2}}{1+t+t^{2}}}.$

Тогда уравнение для y будет

$y=t(x+1)={\frac {t(t+2)}{1+t+t^{2}}}\,,$

что определяет рациональную параметризацию эллипса и, следовательно, показывает, что эллипс является рациональной кривой. Все точки эллипса даны, за исключением (−1,1), что соответствует t = ∞; вся кривая параметризована, следовательно, действительной проективной прямой.

Такая рациональная параметризация может быть рассмотрена в проективном пространстве путем приравнивания первых проективных координат числителям параметризации, а последней — общему знаменателю. Поскольку параметр определен в проективной прямой, многочлены в параметре должны быть гомогенизированы . Например, проективная параметризация эллипса выше имеет вид

$X=U^{2}-T^{2},\quad Y=T\,(T+2\,U),\quad Z=T^{2}+TU+U^{2}.$

Исключая T и U из этих уравнений, мы снова получаем проективное уравнение эллипса , которое можно легко получить непосредственно путем гомогенизации приведенного выше уравнения. $X^{2}+X\,Y+Y^{2}=Z^{2},$

Многие из кривых в списке кривых Википедии являются рациональными и, следовательно, имеют схожие рациональные параметризации.

Рациональные плоские кривые

Рациональные плоские кривые являются рациональными кривыми, вложенными в . Для заданных общих сечений степени однородных многочленов в двух координатах, , существует отображение, заданное определением рациональной плоской кривой степени . ^[2] Существует связанное пространство модулей (где — класс гиперплоскости), параметризующее все такие устойчивые кривые . Можно сделать подсчет размерности для определения размерности пространства модулей: Есть параметры в , дающие параметры в целом для каждого из сечений. Тогда, поскольку они рассматриваются с точностью до проективного отношения в , в имеется меньший параметр . Кроме того, существует трехмерная группа автоморфизмов , следовательно, имеет размерность . Это пространство модулей можно использовать для подсчета количества степенных рациональных плоских кривых, пересекающих точки, с использованием теории Громова–Виттена . ^[3] Оно задается рекурсивным соотношением , где . $\mathbb {P} ^{2}$ $s_{1},s_{2},s_{3}\in \Gamma (\mathbb {P} ^{1},{\mathcal {O}}(d))$ $d$ $x,y$ $s:\mathbb {P} ^{1}\to \mathbb {P} ^{2}$ $s([x:y])=[s_{1}([x:y]):s_{2}([x:y]):s_{3}([x:y])]$ $d$ ${\mathcal {M}}={\overline {\mathcal {M}}}_{0,0}(\mathbb {P} ^{2},d\cdot [H])$ $[H]$ $d+1$ $\Gamma (\mathbb {P} ^{1},{\mathcal {O}}(d))$ $3d+3$ $\mathbb {P} ^{2}$ $1$ ${\mathcal {M}}$ $\mathbb {P} ^{1}$ ${\mathcal {M}}$ $3d+3-1-3=3d-1$ $N_{d}$ $d$ $3d-1$ $N_{d}=\sum _{d_{A}+d_{B}=d}N_{d_{A}}N_{d_{B}}d_{A}^{2}d_{B}\left(d_{B}{\binom {3d-4}{3d_{A}-2}}-d_{A}{\binom {3d-4}{3d_{A}-1}}\right)$ $N_{1}=N_{2}=1$

Эллиптические кривые

Эллиптическая кривая может быть определена как любая кривая рода один с рациональной точкой : общая модель — это невырожденная кубическая кривая , которая достаточна для моделирования любой кривой рода один. В этой модели выделенная точка обычно принимается за точку перегиба на бесконечности; это равносильно требованию, чтобы кривая могла быть записана в форме Тейта-Вейерштрасса, которая в своей проективной версии имеет вид $y^{2}z+a_{1}xyz+a_{3}yz^{2}=x^{3}+a_{2}x^{2}z+a_{4}xz^{2}+a_{6}z^{3}.$

Если характеристика поля отлична от 2 и 3, то линейная замена координат позволяет положить что дает классическую форму Вейерштрасса $a_{1}=a_{2}=a_{3}=0,$ $y^{2}=x^{3}+px+q.$

Эллиптические кривые несут структуру абелевой группы с выделенной точкой как тождеством группового закона. В плоской кубической модели три точки в сумме дают ноль в группе тогда и только тогда, когда они коллинеарны . Для эллиптической кривой, определенной над комплексными числами, группа изоморфна аддитивной группе комплексной плоскости по модулю решетки периодов соответствующих эллиптических функций .

Пересечение двух квадратичных поверхностей , в общем случае, является неособой кривой рода один и степени четыре, и, таким образом, эллиптической кривой, если она имеет рациональную точку. В особых случаях пересечение может быть либо рациональной особой квартикой, либо разлагается на кривые меньших степеней, которые не всегда различны (либо кубическая кривая и прямая, либо две коники, либо коника и две прямые, либо четыре прямые).

Кривые рода больше единицы

Кривые рода больше единицы заметно отличаются как от рациональных, так и от эллиптических кривых. Такие кривые, определенные над рациональными числами, по теореме Фалтингса , могут иметь только конечное число рациональных точек, и их можно рассматривать как имеющие гиперболическую геометрическую структуру. Примерами являются гиперэллиптические кривые , кривая Клейна четвертого порядка и кривая Ферма $x n + y n = z n ,$ когда $n$ больше трех. Также проективные плоские кривые в и кривые в дают много полезных примеров. $\mathbb {P} ^{2}$ $\mathbb {P} ^{1}\times \mathbb {P} ^{1}$

Проективные плоские кривые

Плоские кривые степени , которые могут быть построены как исчезающее локус общего сечения , имеют род , который может быть вычислен с помощью когерентных пучковых когомологий . Вот краткий обзор родов кривых относительно их степени $C\subset \mathbb {P} ^{2}$ $k$ $s\in \Gamma (\mathbb {P} ^{2},{\mathcal {O}}(k))$ ${\frac {(k-1)(k-2)}{2}}$

Например, кривая определяет кривую рода , которая является гладкой, поскольку дифференциалы не имеют общих нулей с кривой.. Непримером общего сечения является кривая , которая, по теореме Безу , должна пересекаться в большинстве точек, является объединением двух рациональных кривых, пересекающихся в двух точках. Примечание задается локусом исчезновения и задается локусом исчезновения . Их можно найти явно: точка лежит в обоих , если . Таким образом, два решения — это точки такие, что , которые являются и . $x^{4}+y^{4}+z^{4}$ $3$ $4x^{3},4y^{3},4z^{3}$ $x(x^{2}+y^{2}+z^{2})$ $2$ $C_{1}\cup C_{2}$ $C_{1}$ $x$ $C_{2}$ $x^{2}+y^{2}+z^{2}$ $x=0$ $[0:y:z]$ $y^{2}+z^{2}=0$ $[0:1:-{\sqrt {-1}}]$ $[0:1:{\sqrt {-1}}]$

Кривые в произведении проективных прямых

Кривая, заданная сходящимся локусом , для , дает кривые рода , которые можно проверить с помощью когомологий когерентного пучка . Если , то они определяют кривые рода , следовательно, кривая любого рода может быть построена как кривая в . Их роды можно суммировать в таблице $C\subset \mathbb {P} ^{1}\times \mathbb {P} ^{1}$ $s\in \Gamma (\mathbb {P} ^{1}\times \mathbb {P} ^{1},{\mathcal {O}}(a,b))$ $a,b\geq 2$ $ab-a-b+1$ $a=2$ $2b-2-b+1=b-1$ $\mathbb {P} ^{1}\times \mathbb {P} ^{1}$

и для , это $a=3$

Смотрите также

Классическая алгебраическая геометрия

Современная алгебраическая геометрия

Геометрия римановых поверхностей

Примечания

^ Хартшорн, Алгебраическая геометрия, IV Пример 1.8.
^ Казарян, Максим Э.; Ландо, Сергей К.; Прасолов, Виктор (2018). Алгебраические кривые: к пространствам модулей. Московские лекции. Springer International Publishing. С. 213–214. ISBN 978-3-030-02942-5.
^ "Формула Концевича для рациональных плоских кривых" (PDF) . Архивировано (PDF) из оригинала 26 февраля 2020 г.

Ссылки

На Викискладе есть медиафайлы по теме Алгебраические кривые .

Брискорн, Эгберт; Кнёррер, Хорст (2013). Плоские алгебраические кривые. Перевод Стиллвелла, Джона. Биркхойзер. ISBN 978-3-0348-5097-1.
Шевалли, Клод (1951). Введение в теорию алгебраических функций одной переменной. Математические обзоры. Т. 6. Американское математическое общество. ISBN 978-0-8218-1506-9.
Кулидж, Джулиан Л. (2004) [1931]. Трактат об алгебраических плоских кривых. Довер. ISBN 978-0-486-49576-7.
Фаркас, Х. М.; Кра, И. (2012) [1980]. Римановы поверхности. Graduate Texts in Mathematics. Том 71. Springer. ISBN 978-1-4684-9930-8.
Фултон, Уильям (1989). Алгебраические кривые: Введение в алгебраическую геометрию. Серия лекций по математике. Том 30 (3-е изд.). Эддисон-Уэсли. ISBN 978-0-201-51010-2.
Гибсон, К. Г. (1998). Элементарная геометрия алгебраических кривых: введение в бакалавриат. Cambridge University Press. ISBN 978-0-521-64641-3.
Гриффитс, Филлип А. (1985). Введение в алгебраические кривые . Перевод математических монографий. Том 70 (3-е изд.). Американское математическое общество. ISBN 9780821845370.
Hartshorne, Robin (2013) [1977]. Алгебраическая геометрия. Graduate Texts in Mathematics. Том 52. Springer. ISBN 978-1-4757-3849-0.
Иитака, Сигеру (2011) [1982]. Алгебраическая геометрия: Введение в бирациональную геометрию алгебраических многообразий. Graduate Texts in Mathematics. Том 76. Springer New York. ISBN 978-1-4613-8121-1.
Милнор, Джон (1968). Особые точки сложных гиперповерхностей. Princeton University Press. ISBN 0-691-08065-8.
Серр, Жан-Пьер (2012) [1988]. Алгебраические группы и поля классов. Graduate Texts in Mathematics. Том 117. Springer. ISBN 978-1-4612-1035-1.
Кёттер, Эрнст (1887). «Основы чисто геометрической теории алгебраических плоских кривых». Труды Королевской академии Берлина .— получил премию Академии 1886 года ^[1]

↑ Норман Фрейзер (февраль 1888 г.). «Синтетическая геометрия алгебраических кривых Кёттера». Труды Эдинбургского математического общества . 7 : 46–61, см. стр. 46.