Коллектор

Топологическое пространство, локально напоминающее евклидово пространство

Бутылка Клейна, погруженная в трехмерное пространство

Поверхность Земли требует (по крайней мере) двух карт, чтобы включить каждую точку. Здесь земной шар разложен на карты вокруг Северного и Южного полюсов .

В математике многообразие — это топологическое пространство , которое локально напоминает евклидово пространство вблизи каждой точки. Точнее, -мерное многообразие, или -многообразие для краткости, — это топологическое пространство со свойством, что каждая точка имеет окрестность , гомеоморфную открытому подмножеству -мерного евклидова пространства. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$

Одномерные многообразия включают линии и окружности , но не самопересекающиеся кривые, такие как восьмёрка . Двумерные многообразия также называются поверхностями . Примерами являются плоскость , сфера и тор , а также бутылка Клейна и действительная проективная плоскость .

Концепция многообразия является центральной для многих разделов геометрии и современной математической физики , поскольку она позволяет описывать сложные структуры в терминах хорошо понятых топологических свойств более простых пространств. Многообразия естественным образом возникают как наборы решений систем уравнений и как графики функций. Эта концепция имеет приложения в компьютерной графике, учитывая необходимость связывать изображения с координатами (например, КТ-сканы ).

Многообразия могут быть снабжены дополнительной структурой. Одним из важных классов многообразий являются дифференцируемые многообразия ; их дифференцируемая структура позволяет выполнять исчисление . Риманова метрика на многообразии позволяет измерять расстояния и углы . Симплектические многообразия служат фазовыми пространствами в гамильтоновом формализме классической механики , в то время как четырехмерные лоренцевы многообразия моделируют пространство-время в общей теории относительности .

Изучение многообразий требует практических знаний исчисления и топологии .

Мотивирующие примеры

Круг

Рисунок 1: Каждая из четырех диаграмм отображает часть круга в открытый интервал, а вместе они покрывают весь круг.

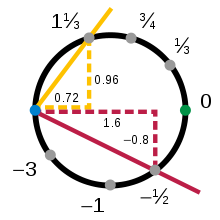
После прямой простейшим примером топологического многообразия является окружность. Топология игнорирует изгибание, поэтому небольшой участок окружности рассматривается так же, как и небольшой участок прямой. Рассмотрим, например, верхнюю часть единичной окружности , x ²  +  y ²  = 1, где координата y положительна (обозначена желтой дугой на рисунке 1 ). Любая точка этой дуги может быть однозначно описана ее координатой x . Таким образом, проекция на первую координату является непрерывным и обратимым отображением из верхней дуги в открытый интервал (−1, 1): $${\displaystyle \chi _{\mathrm {top} }(x,y)=x.\,}$$

Такие функции вместе с открытыми областями, которые они отображают, называются диаграммами . Аналогично существуют диаграммы для нижней (красной), левой (синей) и правой (зеленой) частей круга: $${\displaystyle {\begin{aligned}\chi _{\mathrm {bottom} }(x,y)&=x\\\chi _{\mathrm {left} }(x,y)&=y\\\chi _{\mathrm {right} }(x,y)&=y.\end{aligned}}}$$

Вместе эти части охватывают весь круг, а четыре карты образуют атлас круга.

Верхняя и правая диаграммы, и соответственно, перекрываются в своей области: их пересечение лежит в четверти круга, где обе и -координаты положительны. Обе отображают эту часть в интервал , хотя и по-разному. Таким образом, можно построить функцию , которая возвращает значения из области определения обратно в круг с помощью обратной функции, а затем обратно в интервал. Если a - любое число в , то: ${\displaystyle \chi _{\mathrm {top} }}$ ${\displaystyle \chi _{\mathrm {right} }}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle (0,1)}$ ${\displaystyle T:(0,1)\rightarrow (0,1)=\chi _{\mathrm {right} }\circ \chi _{\mathrm {top} }^{-1}}$ ${\displaystyle \chi _{\mathrm {top} }}$ ${\displaystyle \chi _{\mathrm {right} }}$ ${\displaystyle (0,1)}$ $${\displaystyle {\begin{aligned}T(a)&=\chi _{\mathrm {right} }\left(\chi _{\mathrm {top} }^{-1}\left[a\right]\right)\\&=\chi _{\mathrm {right} }\left(a,{\sqrt {1-a^{2}}}\right)\\&={\sqrt {1-a^{2}}}\end{aligned}}}$$

Такая функция называется картой перехода .

Рисунок 2: Диаграмма кругового многообразия, основанная на наклоне, охватывающая все точки круга, кроме одной.

Верхняя, нижняя, левая и правая диаграммы не образуют единственный возможный атлас. Диаграммы не обязательно должны быть геометрическими проекциями, а количество диаграмм — вопрос выбора. Рассмотрите диаграммы и $${\displaystyle \chi _{\mathrm {minus} }(x,y)=s={\frac {y}{1+x}}}$$ $${\displaystyle \chi _{\mathrm {plus} }(x,y)=t={\frac {y}{1-x}}}$$

Здесь s — наклон линии, проходящей через точку с координатами ( x ,  y ) и фиксированную точку поворота (−1, 0); аналогично, t — противоположность наклона линии, проходящей через точки с координатами ( x ,  y ) и (+1, 0). Обратное отображение из s в ( x ,  y ) задается формулой $${\displaystyle {\begin{aligned}x&={\frac {1-s^{2}}{1+s^{2}}}\\[5pt]y&={\frac {2s}{1+s^{2}}}\end{aligned}}}$$

Можно подтвердить, что x ²  +  y ²  = 1 для всех значений s и t . Эти две диаграммы представляют собой второй атлас для окружности с картой перехода (то есть, существует эта связь между s и t для каждой точки, где s и t оба не равны нулю). $${\displaystyle t={\frac {1}{s}}}$$

Каждая диаграмма пропускает одну точку, либо (−1, 0) для s , либо (+1, 0) для t , поэтому ни одна диаграмма в отдельности недостаточна для покрытия всего круга. Можно доказать, что невозможно покрыть весь круг одной диаграммой. Например, хотя можно построить круг из одного интервала линии, наложив и «склеив» концы, это не даст диаграмму; часть круга будет отображена на оба конца одновременно, потеряв обратимость.

Сфера

Сфера является примером поверхности. Единичная сфера неявного уравнения

х2 + у2 + z2 ^{– 1} = ⁰

может быть покрыта атласом из шести карт : плоскость z = 0 делит сферу на две полусферы ( z > 0 и z < 0 ), которые обе могут быть отображены на диске x ² + y ² < 1 проекцией на плоскость координат xy . Это дает две карты; четыре другие карты предоставляются аналогичной конструкцией с двумя другими координатными плоскостями.

Как и в случае с окружностью, можно определить одну карту, которая покрывает всю сферу, за исключением одной точки. Таким образом, двух карт достаточно, но сфера не может быть покрыта одной картой.

Этот пример имеет историческое значение, поскольку он мотивировал терминологию; стало очевидно, что вся поверхность Земли не может иметь плоскостного представления, состоящего из одной карты (также называемой «картой», см. морская карта ), и поэтому необходимы атласы для покрытия всей поверхности Земли.

Другие кривые

Четыре многообразия из алгебраических кривых : ■  окружности, ■  параболы, ■  гиперболы, ■  куба.

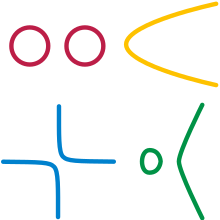
Коллекторы не обязательно должны быть соединены (все в «одном целостном» виде); примером может служить пара отдельных окружностей.

Многообразия не обязательно должны быть замкнутыми ; таким образом, отрезок прямой без конечных точек является многообразием. Они никогда не являются счетными , если только размерность многообразия не равна 0. Объединяя эти свободы, другими примерами многообразий являются парабола , гипербола и геометрическое место точек на кубической кривой y ² = x ³ − x (замкнутый петлевой участок и открытый бесконечный участок).

Однако исключаются примеры, такие как два соприкасающихся круга, которые имеют общую точку, образуя восьмерку; в общей точке не может быть создана удовлетворительная диаграмма. Даже с изгибом, допускаемым топологией, окрестность общей точки выглядит как "+", а не как линия. "+" не гомеоморфен отрезку прямой, поскольку удаление центральной точки из "+" дает пространство с четырьмя компонентами (т. е. частями), тогда как удаление точки из отрезка прямой дает пространство с максимум двумя частями; топологические операции всегда сохраняют количество частей.

Математическое определение

Неформально, многообразие — это пространство , «созданное по образцу» евклидова пространства.

Существует много различных видов многообразий. В геометрии и топологии все многообразия являются топологическими многообразиями , возможно, с дополнительной структурой. Многообразие можно построить, задав набор координатных карт, то есть покрытие открытыми множествами с гомеоморфизмами в евклидово пространство, и функции заплатки ^{[ необходимо разъяснение ]} : гомеоморфизмы из одной области евклидова пространства в другую область, если они соответствуют одной и той же части многообразия в двух различных координатных картах. Многообразию можно придать дополнительную структуру, если функции заплатки удовлетворяют аксиомам за пределами непрерывности. Например, дифференцируемые многообразия имеют гомеоморфизмы на перекрывающихся окрестностях, диффеоморфных друг другу, так что многообразие имеет четко определенный набор функций, которые дифференцируемы в каждой окрестности, таким образом, дифференцируемы на многообразии в целом.

Формально (топологическое) многообразие — это хаусдорфово пространство, удовлетворяющее второй аксиоме счетности , локально гомеоморфное евклидову пространству.

Вторая счетность и Хаусдорфовость являются условиями точечного множества ; вторая счетность исключает пространства, которые в некотором смысле «слишком велики», такие как длинная линия , в то время как Хаусдорф исключает пространства, такие как «линия с двумя началами» (эти обобщения многообразий обсуждаются в разделе Нехаусдорфовы многообразия ).

Локальная гомеоморфность евклидову пространству означает, что каждая точка имеет окрестность, гомеоморфную открытому подмножеству евклидова пространства для некоторого неотрицательного целого числа n . ${\displaystyle \mathbb {R} ^{n},}$

Это означает, что либо точка является изолированной точкой (если ), либо она имеет окрестность, гомеоморфную открытому шару Это также означает, что каждая точка имеет окрестность, гомеоморфную , поскольку гомеоморфна и даже диффеоморфна любому открытому шару в ней (при ). ${\displaystyle n=0}$ $${\displaystyle \mathbf {B} ^{n}=\left\{(x_{1},x_{2},\dots ,x_{n})\in \mathbb {R} ^{n}:x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}<1\right\}.}$$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n>0}$

Число n , которое появляется в предыдущем определении, называется локальной размерностью многообразия. Обычно многообразия считаются имеющими постоянную локальную размерность, и тогда локальная размерность называется размерностью многообразия . Это, в частности, имеет место, когда многообразия связаны . Однако некоторые авторы допускают многообразия, которые не связаны, и где разные точки могут иметь разные размерности . ^[1] Если многообразие имеет фиксированную размерность, это можно подчеркнуть, назвав егочистое многообразие . Например, (поверхность) сферы имеет постоянную размерность 2 и, следовательно, является чистым многообразием, тогда какнесвязное объединениесферы и линии в трехмерном пространственечистым многообразием. Поскольку размерность является локальным инвариантом (т. е. отображение, отправляющее каждую точку в размерность ее окрестности, над которой определена карта, являетсялокально постоянной), каждыйсвязный компонентимеет фиксированную размерность.

С точки зрения теории пучков многообразие — это локально окольцованное пространство , структурный пучок которого локально изоморфен пучку непрерывных (или дифференцируемых, или комплексно-аналитических и т. д.) функций на евклидовом пространстве. Это определение в основном используется при обсуждении аналитических многообразий в алгебраической геометрии .

Карты, атласы и карты переходов

Навигация по сферической Земле осуществляется с помощью плоских карт или диаграмм, собранных в атласе. Аналогично, многообразие можно описать с помощью математических карт , называемых координатными диаграммами , собранных в математическом атласе . Обычно невозможно описать многообразие с помощью только одной диаграммы, поскольку глобальная структура многообразия отличается от простой структуры диаграмм. Например, ни одна плоская карта не может представлять всю Землю без разделения смежных объектов по границам карты или дублирования покрытия. Когда многообразие создается из нескольких перекрывающихся диаграмм, регионы, где они перекрываются, несут информацию, необходимую для понимания глобальной структуры.

Диаграммы

Координатная карта , координатная карта или просто карта многообразия — это обратимое отображение между подмножеством многообразия и простым пространством, такое, что и отображение, и его обратное сохраняют желаемую структуру. ^[2] Для топологического многообразия простое пространство является подмножеством некоторого евклидова пространства , и интерес сосредоточен на топологической структуре. Эта структура сохраняется гомеоморфизмами , обратимыми отображениями, которые непрерывны в обоих направлениях. ${\displaystyle \mathbb {R} ^{n}}$

В случае дифференцируемого многообразия набор карт, называемых атласом , чьи переходные функции (см. ниже) все дифференцируемы, позволяет нам выполнять исчисление на нем. Полярные координаты , например, образуют карту для плоскости за вычетом положительной оси x и начала координат. Другим примером карты является упомянутая выше карта χ _top , карта для окружности. ${\displaystyle \mathbb {R} ^{2}}$

Атласы

Описание большинства многообразий требует более одной диаграммы. Определенный набор диаграмм, покрывающий многообразие, называется атласом . Атлас не является уникальным, поскольку все многообразия могут быть покрыты несколькими способами с использованием различных комбинаций диаграмм. Два атласа называются эквивалентными, если их объединение также является атласом.

Атлас, содержащий все возможные карты, соответствующие данному атласу, называется максимальным атласом (т. е. классом эквивалентности, содержащим данный атлас). В отличие от обычного атласа, максимальный атлас данного многообразия уникален. Хотя он полезен для определений, он является абстрактным объектом и не используется напрямую (например, в вычислениях).

Карты перехода

Карты в атласе могут перекрываться, и одна точка многообразия может быть представлена ​​на нескольких картах. Если две карты перекрываются, их части представляют одну и ту же область многообразия, так же как карта Европы и карта России могут обе содержать Москву. Учитывая две перекрывающиеся карты, можно определить функцию перехода , которая идет от открытого шара в к многообразию и затем обратно к другому (или, возможно, тому же самому) открытому шару в . Результирующая карта, как и карта T в примере с окружностью выше, называется изменением координат , преобразованием координат , функцией перехода или картой перехода . ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Дополнительная структура

Атлас также может использоваться для определения дополнительной структуры на коллекторе. Сначала структура определяется на каждой карте отдельно. Если все карты перехода совместимы с этой структурой, структура переносится на коллектор.

Это стандартный способ определения дифференцируемых многообразий. Если функции перехода атласа для топологического многообразия сохраняют естественную дифференциальную структуру (то есть, если они являются диффеоморфизмами ), дифференциальная структура переносится на многообразие и превращает его в дифференцируемое многообразие. Комплексные многообразия вводятся аналогичным образом, требуя, чтобы функции перехода атласа были голоморфными функциями . Для симплектических многообразий функции перехода должны быть симплектоморфизмами . ${\displaystyle \mathbb {R} ^{n}}$

Структура на многообразии зависит от атласа, но иногда можно сказать, что разные атласы порождают одну и ту же структуру. Такие атласы называются совместимыми .

Эти понятия в общем случае уточняются посредством использования псевдогрупп .

Коллектор с границей

Гладкое 2-многообразие: Внутренняя карта с отображением перехода φ ₁ отображает открытое подмножество вокруг внутренней точки в открытое евклидово подмножество, в то время как граничная карта с отображением перехода φ ₂ отображает замкнутое подмножество вокруг граничной точки в замкнутое евклидово подмножество. Граница сама по себе является 1 -многообразием без границы, поэтому карта с отображением перехода φ ₃ должна отображать открытое евклидово подмножество.

Многообразие с границей — это многообразие с краем. Например, лист бумаги — это 2-многообразие с 1-мерной границей. Граница 2-многообразия с границей — это 2-многообразие. Диск (круг плюс внутренность) — это 2-многообразие с границей. Его граница — круг, 1-многообразие . Квадрат с внутренностью — это также 2-многообразие с границей. Шар (сфера плюс внутренность) — это 3-многообразие с границей. Его граница — сфера, 2-многообразие. (Не путайте с границей (топология) ). ${\displaystyle n}$ ${\displaystyle (n-1)}$

На техническом языке многообразие с границей — это пространство, содержащее как внутренние, так и граничные точки. Каждая внутренняя точка имеет окрестность, гомеоморфную открытому -шару . Каждая граничная точка имеет окрестность, гомеоморфную "половине" -шару . Любой гомеоморфизм между полушарами должен переводить точки с в точки с . Эта инвариантность позволяет "определять" граничные точки; см. следующий абзац. ${\displaystyle n}$ ${\displaystyle \{(x_{1},x_{2},\dots ,x_{n})\vert \Sigma x_{i}^{2}<1\}}$ ${\displaystyle n}$ ${\displaystyle \{(x_{1},x_{2},\dots ,x_{n})\vert \Sigma x_{i}^{2}<1{\text{ and }}x_{1}\geq 0\}}$ ${\displaystyle x_{1}=0}$ ${\displaystyle x_{1}=0}$

Граница и интерьер

Пусть будет многообразием с границей. Внутренность , обозначаемая , представляет собой множество точек, в которых есть окрестности, гомеоморфные открытому подмножеству . Граница , обозначаемая , представляет собой дополнение к в . Граничные точки можно охарактеризовать как те точки, которые попадают на граничную гиперплоскость под некоторой координатной картой. ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle \operatorname {Int} M}$ ${\displaystyle M}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle M}$ ${\displaystyle \partial M}$ ${\displaystyle \operatorname {Int} M}$ ${\displaystyle M}$ ${\displaystyle (x_{n}=0)}$ ${\displaystyle \mathbb {R} _{+}^{n}}$

Если — многообразие с границей размерности , то — многообразие (без границы) размерности и — многообразие (без границы) размерности . ${\displaystyle M}$ ${\displaystyle n}$ ${\displaystyle \operatorname {Int} M}$ ${\displaystyle n}$ ${\displaystyle \partial M}$ ${\displaystyle n-1}$

Строительство

Один и тот же коллектор может быть построен разными способами, каждый из которых подчеркивает отдельный аспект коллектора, тем самым приводя к несколько иной точке зрения.

Диаграммы

На диаграмме часть сферы с положительной координатой z отображается в виде диска.

Возможно, самый простой способ построения многообразия — это тот, который используется в примере выше для окружности. Сначала определяется подмножество , а затем строится атлас, покрывающий это подмножество. Концепция многообразия исторически выросла из таких конструкций. Вот еще один пример, применяющий этот метод к построению сферы: ${\displaystyle \mathbb {R} ^{2}}$

Сфера с диаграммами

Сферу можно рассматривать почти так же, как и окружность. В математике сфера — это просто поверхность (не твердая внутренняя часть), которую можно определить как подмножество : ${\displaystyle \mathbb {R} ^{3}}$ $${\displaystyle S=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}+z^{2}=1\right\}.}$$

Сфера двумерна, поэтому каждая диаграмма будет отображать часть сферы в открытое подмножество . Рассмотрим северное полушарие, которое является частью с положительной координатой z (окрашено красным на рисунке справа). Функция χ определяется как ${\displaystyle \mathbb {R} ^{2}}$ $${\displaystyle \chi (x,y,z)=(x,y),\ }$$

отображает северное полушарие на открытый единичный диск , проецируя его на плоскость ( x , y ). Аналогичная карта существует для южного полушария. Вместе с двумя картами, проецирующимися на плоскость ( x , z ), и двумя картами, проецирующимися на плоскость ( y , z ), получается атлас из шести карт, который покрывает всю сферу.

Это можно легко обобщить на сферы более высоких измерений.

Пэчворк

Многообразие может быть построено путем склеивания частей в согласованной манере, превращая их в перекрывающиеся диаграммы. Такое построение возможно для любого многообразия и, следовательно, часто используется в качестве характеристики, особенно для дифференцируемых и римановых многообразий. Оно фокусируется на атласе, поскольку патчи естественным образом предоставляют диаграммы, и поскольку не задействовано внешнее пространство, это приводит к внутреннему виду многообразия.

Многообразие строится путем указания атласа, который сам определяется переходными картами. Таким образом, точка многообразия является классом эквивалентности точек, которые отображаются друг на друга переходными картами. Карты отображают классы эквивалентности в точки одного участка. Обычно существуют строгие требования к согласованности переходных карт. Для топологических многообразий они должны быть гомеоморфизмами; если они также являются диффеоморфизмами, то полученное многообразие является дифференцируемым многообразием.

Это можно проиллюстрировать с помощью карты перехода t = ¹ ⁄ _s из примера второй половины окружности. Начните с двух копий линии. Используйте координату s для первой копии и t для второй копии. Теперь склейте обе копии вместе, отождествив точку t на второй копии с точкой s = ¹ ⁄ _t на первой копии (точки t = 0 и s = 0 не отождествляются ни с одной точкой на первой и второй копии соответственно). Это дает окружность.

Внутренний и внешний вид

Первая конструкция и эта конструкция очень похожи, но представляют довольно разные точки зрения. В первой конструкции многообразие рассматривается как вложенное в некоторое евклидово пространство. Это внешний вид . Когда многообразие рассматривается таким образом, легко использовать интуицию из евклидовых пространств для определения дополнительной структуры. Например, в евклидовом пространстве всегда ясно, является ли вектор в некоторой точке касательным или нормальным к некоторой поверхности, проходящей через эту точку.

Конструкция пэчворка не использует никакого вложения, а просто рассматривает многообразие как топологическое пространство само по себе. Эта абстрактная точка зрения называется внутренним представлением . Это может затруднить представление о том, каким может быть касательный вектор, и нет внутреннего понятия нормального расслоения , но вместо этого есть внутреннее стабильное нормальное расслоение .

н-Сфера как лоскутное одеяло

N -сфера S ⁿ является обобщением идеи круга (1-сфера) и сферы (2-сфера) на более высокие измерения. N -сфера S ⁿ может быть построена путем склеивания двух копий . Переходное отображение между ними является инверсией в сфере , определяемой как ${\displaystyle \mathbb {R} ^{n}}$ $${\displaystyle \mathbb {R} ^{n}\setminus \{0\}\to \mathbb {R} ^{n}\setminus \{0\}:x\mapsto x/\|x\|^{2}.}$$

Эта функция является своей собственной обратной и, таким образом, может использоваться в обоих направлениях. Поскольку отображение перехода является гладкой функцией , этот атлас определяет гладкое многообразие. В случае n = 1 пример упрощается до примера окружности, приведенного ранее.

Определение точек многообразия

Можно определить различные точки многообразия как одну и ту же точку. Это можно визуализировать как склеивание этих точек в одной точке, образуя факторпространство . Однако нет никаких оснований ожидать, что такие факторпространства будут многообразиями. Среди возможных факторпространств, которые не обязательно являются многообразиями, орбифолды и комплексы CW считаются относительно хорошо ведущими себя . Примером факторпространства многообразия, которое также является многообразием, является действительное проективное пространство , идентифицированное как факторпространство соответствующей сферы.

Один из методов идентификации точек (склеивания их вместе) заключается в правом (или левом) действии группы , которая действует на многообразие. Две точки идентифицируются, если одна перемещается на другую некоторым элементом группы. Если M — многообразие, а G — группа, то результирующее факторпространство обозначается как M / G (или G \ M ).

Многообразия, которые можно построить путем идентификации точек, включают торы и действительные проективные пространства (начиная с плоскости и сферы соответственно).

Склеивание по границам

Два многообразия с границами можно склеить вдоль границы. Если это сделано правильно, то результатом также будет многообразие. Аналогично можно склеить два края одного многообразия.

Формально склеивание определяется биекцией между двумя границами ^{[ dubious – discussion ]} . Две точки идентифицируются, когда они отображаются друг на друга. Для топологического многообразия эта биекция должна быть гомеоморфизмом, иначе результат не будет топологическим многообразием. Аналогично, для дифференцируемого многообразия это должен быть диффеоморфизм. Для других многообразий должны сохраняться другие структуры.

Конечный цилиндр может быть построен как многообразие, начиная с полосы [0,1] × [0,1] и склеивая пару противоположных рёбер на границе с помощью подходящего диффеоморфизма. Проективная плоскость может быть получена склеиванием сферы с отверстием в ней с лентой Мёбиуса вдоль их соответствующих круговых границ.

Декартовы произведения

Декартово произведение многообразий также является многообразием.

Размерность многообразия-произведения равна сумме размерностей его факторов. Его топология — топология произведения , а декартово произведение карт — это карта для многообразия-произведения. Таким образом, атлас для многообразия-произведения может быть построен с использованием атласов для его факторов. Если эти атласы определяют дифференциальную структуру на факторах, соответствующий атлас определяет дифференциальную структуру на многообразии-произведении. То же самое верно для любой другой структуры, определенной на факторах. Если один из факторов имеет границу, многообразие-произведение также имеет границу. Декартовы произведения могут быть использованы для построения торов и конечных цилиндров , например, как S ¹  ×  S ¹ и S ¹  × [0,1] соответственно.

Конечный цилиндр — это многообразие с границей.

История

Изучение многообразий объединяет многие важные области математики: оно обобщает такие понятия, как кривые и поверхности, а также идеи линейной алгебры и топологии.

Раннее развитие

Современной концепции многообразия предшествовало несколько важных результатов.

Неевклидова геометрия рассматривает пространства, в которых постулат параллельности Евклида неверен . Саккери впервые изучил такие геометрии в 1733 году, но стремился только опровергнуть их. Гаусс , Бойяи и Лобачевский независимо друг от друга открыли их 100 лет спустя. Их исследования выявили два типа пространств, геометрическая структура которых отличается от структуры классического евклидова пространства; они дали начало гиперболической геометрии и эллиптической геометрии . В современной теории многообразий эти понятия соответствуют римановым многообразиям с постоянной отрицательной и положительной кривизной соответственно.

Карл Фридрих Гаусс, возможно, был первым, кто рассматривал абстрактные пространства как математические объекты как таковые. Его Theorema egregium дает метод вычисления кривизны поверхности без учета окружающего пространства, в котором лежит поверхность. Такая поверхность, в современной терминологии, называлась бы многообразием; и в современных терминах теорема доказывает, что кривизна поверхности является внутренним свойством . Теория многообразий стала фокусироваться исключительно на этих внутренних свойствах (или инвариантах), в то время как внешние свойства окружающего пространства в значительной степени игнорируются.

Другим, более топологическим примером внутреннего свойства многообразия является его эйлерова характеристика . Леонард Эйлер показал, что для выпуклого многогранника в трехмерном евклидовом пространстве с V вершинами (или углами), E ребрами и F гранями, Та же самая формула будет верна, если мы спроецируем вершины и ребра многогранника на сферу, создав топологическую карту с V вершинами, E ребрами и F гранями, и фактически останется верной для любой сферической карты, даже если она не возникает из какого-либо выпуклого многогранника. ^[3] Таким образом, 2 является топологическим инвариантом сферы, называемым ее эйлеровой характеристикой . С другой стороны, тор можно разрезать его «параллельными» и «меридианными» окружностями, создав карту с V  = 1 вершиной, E  = 2 ребрами и F  = 1 гранью. Таким образом, эйлерова характеристика тора равна 1 − 2 + 1 = 0. Эйлерова характеристика других поверхностей является полезным топологическим инвариантом , который может быть расширен до более высоких размерностей с помощью чисел Бетти . В середине девятнадцатого века теорема Гаусса–Бонне связала эйлерову характеристику с гауссовой кривизной . $${\displaystyle V-E+F=2.\ }$$

Синтез

Исследования Нильса Хенрика Абеля и Карла Густава Якоби по обращению эллиптических интегралов в первой половине 19 века привели их к рассмотрению специальных типов комплексных многообразий, ныне известных как якобианы . Бернхард Риман внес дальнейший вклад в их теорию, прояснив геометрический смысл процесса аналитического продолжения функций комплексных переменных.

Другим важным источником многообразий в математике 19 века была аналитическая механика , разработанная Симеоном Пуассоном , Якоби и Уильямом Роуэном Гамильтоном . Возможные состояния механической системы считаются точками абстрактного пространства, фазового пространства в лагранжевом и гамильтоновом формализмах классической механики. Это пространство, по сути, является многообразием высокой размерности, размерность которого соответствует степеням свободы системы, а точки задаются их обобщенными координатами . Для неограниченного движения свободных частиц многообразие эквивалентно евклидову пространству, но различные законы сохранения ограничивают его более сложными образованиями, например торами Лиувилля. Теория вращающегося твердого тела, разработанная в 18 веке Леонардом Эйлером и Жозефом-Луи Лагранжем , дает еще один пример, где многообразие нетривиально. Геометрические и топологические аспекты классической механики были подчеркнуты Анри Пуанкаре , одним из основателей топологии.

Риман был первым, кто проделал обширную работу по обобщению идеи поверхности на более высокие измерения. Название «многообразие» происходит от оригинального немецкого термина Римана, Mannigfaltigkeit , который Уильям Кингдон Клиффорд перевел как «многообразие». В своей вступительной лекции в Геттингене Риман описал множество всех возможных значений переменной с определенными ограничениями как Mannigfaltigkeit , поскольку переменная может иметь много значений. Он различает stetige Mannigfaltigkeit и discrete Mannigfaltigkeit ( непрерывное многообразие и прерывное многообразие ) в зависимости от того, изменяется ли значение непрерывно или нет. В качестве непрерывных примеров Риман ссылается не только на цвета и расположение объектов в пространстве, но и на возможные формы пространственной фигуры. Используя индукцию , Риман строит n-fach ausgedehne Mannigfaltigkeit ( n times extended multipleness или n-мерное многообразие ) как непрерывный стек (n−1)-мерных многообразий. Интуитивное понятие Римана о Mannigfaltigkeit развилось в то, что сегодня формализуется как многообразие. Римановы многообразия и римановы поверхности названы в честь Римана.

Определение Пуанкаре

В своей очень влиятельной статье «Анализ положения» [ ^4] Анри Пуанкаре дал определение дифференцируемого многообразия ( variété ), которое послужило предшественником современной концепции многообразия. ^[5]

В первом разделе Analysis Situs Пуанкаре определяет многообразие как множество уровня непрерывно дифференцируемой функции между евклидовыми пространствами, которое удовлетворяет гипотезе невырожденности теоремы о неявной функции . В третьем разделе он начинает с замечания о том, что график непрерывно дифференцируемой функции является многообразием в последнем смысле. Затем он предлагает новое, более общее определение многообразия, основанное на «цепи многообразий» ( une chaîne des variétés ).

Понятие Пуанкаре о цепи многообразий является предшественником современного понятия атласа. В частности, он рассматривает два многообразия, определяемые соответственно как графики функций и . Если эти многообразия перекрываются ( a une partie commune ), то он требует, чтобы координаты непрерывно дифференцируемо зависели от координат и наоборот (' ...les sont fonctions analytiques des et inversement '). Таким образом, он вводит предшественника понятия карты и отображения перехода. ${\displaystyle \theta (y)}$ ${\displaystyle \theta '\left(y'\right)}$ ${\displaystyle y}$ ${\displaystyle y'}$ ${\displaystyle y}$ ${\displaystyle y'}$

Например, единичную окружность на плоскости можно рассматривать как график функции или же функцию в окрестности каждой точки, за исключением точек (1, 0) и (−1, 0); а в окрестности этих точек ее можно рассматривать как график, соответственно, и . Окружность можно представить графиком в окрестности каждой точки, поскольку левая часть ее определяющего уравнения имеет ненулевой градиент в каждой точке окружности. По теореме о неявной функции каждое подмногообразие евклидова пространства локально является графиком функции. ${\textstyle y={\sqrt {1-x^{2}}}}$ ${\textstyle y=-{\sqrt {1-x^{2}}}}$ ${\textstyle x={\sqrt {1-y^{2}}}}$ ${\textstyle x=-{\sqrt {1-y^{2}}}}$ ${\displaystyle x^{2}+y^{2}-1=0}$

Герман Вейль дал внутреннее определение для дифференцируемых многообразий в своем курсе лекций по римановым поверхностям в 1911–1912 годах, открыв дорогу к общей концепции топологического пространства , которая вскоре последовала. В 1930-х годах Хасслер Уитни и другие прояснили основополагающие аспекты предмета, и таким образом интуиции, восходящие ко второй половине 19 века, стали точными и развитыми через дифференциальную геометрию и теорию групп Ли . В частности, теорема вложения Уитни ^[6] показала, что внутреннее определение в терминах карт эквивалентно определению Пуанкаре в терминах подмножеств евклидова пространства.

Топология многообразий: основные моменты

Двумерные многообразия, также известные как 2D- поверхности , вложенные в наше общее 3D-пространство, были рассмотрены Риманом под видом римановых поверхностей и строго классифицированы в начале 20-го века Полом Хегором и Максом Деном . Пуанкаре был пионером в изучении трехмерных многообразий и поднял фундаментальный вопрос о них, сегодня известный как гипотеза Пуанкаре . Спустя почти столетие Григорий Перельман доказал гипотезу Пуанкаре (см. Решение гипотезы Пуанкаре ). Программа геометризации Уильяма Терстона , сформулированная в 1970-х годах, обеспечила далеко идущее расширение гипотезы Пуанкаре на общие трехмерные многообразия. Четырехмерные многообразия были выведены на передний план математических исследований в 1980-х годах Майклом Фридманом и, в другой обстановке, Саймоном Дональдсоном , который был мотивирован недавним прогрессом в теоретической физике ( теория Янга–Миллса ), где они служат заменой обычного «плоского» пространства-времени . Андрей Марков-младший показал в 1960 году, что не существует алгоритма для классификации четырехмерных многообразий. Важная работа по многообразиям более высоких размерностей, включая аналоги гипотезы Пуанкаре , была ранее проделана Рене Томом , Джоном Милнором , Стивеном Смейлом и Сергеем Новиковым . Весьма распространенной и гибкой техникой, лежащей в основе многих работ по топологии многообразий, является теория Морса .

Дополнительная структура

Топологические многообразия

Самый простой для определения вид многообразия — это топологическое многообразие, которое локально выглядит как некоторое «обычное» евклидово пространство . По определению, все многообразия являются топологическими многообразиями, поэтому фраза «топологическое многообразие» обычно используется, чтобы подчеркнуть, что многообразие не имеет дополнительной структуры или что рассматриваются только его топологические свойства. Формально топологическое многообразие — это топологическое пространство, локально гомеоморфное евклидову пространству. Это означает, что у каждой точки есть окрестность, для которой существует гомеоморфизм ( биективная непрерывная функция, обратная к которой также непрерывна), отображающий эту окрестность в . Эти гомеоморфизмы являются картами многообразия. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Топологическое многообразие локально выглядит как евклидово пространство в довольно слабой манере: в то время как для каждой отдельной карты можно различать дифференцируемые функции или измерять расстояния и углы, просто в силу того, что оно является топологическим многообразием, пространство не имеет какого-либо конкретного и последовательного выбора таких понятий. ^[7] Для того чтобы обсудить такие свойства для многообразия, необходимо указать дополнительную структуру и рассмотреть дифференцируемые многообразия и римановы многообразия, обсуждаемые ниже. В частности, одно и то же базовое топологическое многообразие может иметь несколько взаимно несовместимых классов дифференцируемых функций и бесконечное число способов указания расстояний и углов.

Обычно делаются дополнительные технические предположения о топологическом пространстве, чтобы исключить патологические случаи. Принято требовать, чтобы пространство было хаусдорфовым и счетным во второй степени .

Размерность многообразия в определенной точке — это размерность евклидова пространства, в которое отображаются карты в этой точке (число n в определении). Все точки в связном многообразии имеют одинаковую размерность. Некоторые авторы требуют, чтобы все карты топологического многообразия отображались в евклидовы пространства той же размерности. В этом случае каждое топологическое многообразие имеет топологический инвариант — свою размерность.

Дифференцируемые многообразия

Для большинства приложений используется специальный вид топологического многообразия, а именно, дифференцируемое многообразие . Если локальные карты на многообразии совместимы в определенном смысле, можно определить направления, касательные пространства и дифференцируемые функции на этом многообразии. В частности, можно использовать исчисление на дифференцируемом многообразии. Каждая точка n -мерного дифференцируемого многообразия имеет касательное пространство . Это n -мерное евклидово пространство, состоящее из касательных векторов кривых, проходящих через точку.

Два важных класса дифференцируемых многообразий — это гладкие и аналитические многообразия . Для гладких многообразий отображения перехода гладкие, то есть бесконечно дифференцируемые. Аналитические многообразия — это гладкие многообразия с дополнительным условием, что отображения перехода являются аналитическими (они могут быть выражены как степенные ряды ). Сфере можно придать аналитическую структуру, как и большинству знакомых кривых и поверхностей.

Спрямляемое множество обобщает идею кусочно-гладкой или спрямляемой кривой на более высокие размерности; однако спрямляемые множества в общем случае не являются многообразиями.

Римановы многообразия

Для измерения расстояний и углов на многообразиях многообразие должно быть римановым. Риманово многообразие — это дифференцируемое многообразие, в котором каждое касательное пространство снабжено скалярным произведением способом, который плавно меняется от точки к точке. При наличии двух касательных векторов и скалярное произведение дает действительное число. Скалярное произведение является типичным примером скалярного произведения. Это позволяет определять различные понятия, такие как длина, углы , площади (или объемы ), кривизна и расхождение векторных полей . ${\displaystyle \langle \cdot ,\cdot \rangle }$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle \langle u,v\rangle }$

Всем дифференцируемым многообразиям (постоянной размерности) можно придать структуру риманова многообразия. Само евклидово пространство несет естественную структуру риманова многообразия (касательные пространства естественным образом отождествляются с самим евклидовым пространством и несут стандартное скалярное произведение пространства). Многие знакомые кривые и поверхности, включая, например, все n -сферы, определяются как подпространства евклидова пространства и наследуют метрику от своего вложения в него.

Финслеровы коллекторы

Многообразие Финслера позволяет определить расстояние, но не требует понятия угла; это аналитическое многообразие, в котором каждое касательное пространство снабжено нормой , , таким образом, который плавно меняется от точки к точке. Эта норма может быть расширена до метрики , определяющей длину кривой; но в общем случае она не может быть использована для определения внутреннего произведения. ${\displaystyle \|\cdot \|}$

Любое риманово многообразие является финслеровым многообразием.

Группы Ли

Группы Ли , названные в честь Софуса Ли , представляют собой дифференцируемые многообразия, которые также несут в себе структуру группы , которая такова, что групповые операции определяются гладкими отображениями.

Евклидово векторное пространство с групповой операцией сложения векторов является примером некомпактной группы Ли. Простым примером компактной группы Ли является окружность: групповая операция — просто вращение. Эту группу, известную как , можно также охарактеризовать как группу комплексных чисел по модулю 1 с умножением в качестве групповой операции. ${\displaystyle \operatorname {U} (1)}$

Другие примеры групп Ли включают специальные группы матриц , которые все являются подгруппами общей линейной группы , группы матриц с ненулевым определителем. Если элементы матрицы являются действительными числами , это будет -мерное несвязное многообразие. Ортогональные группы , группы симметрии сферы и гиперсфер , являются размерными многообразиями, где - размерность сферы. Дополнительные примеры можно найти в таблице групп Ли . ${\displaystyle n\times n}$ ${\displaystyle n^{2}}$ ${\displaystyle n(n-1)/2}$ ${\displaystyle n-1}$

Другие типы коллекторов

• Комплексное многообразие — это многообразие, карты которого принимают значения в и чьи переходные функции голоморфны на перекрытиях. Эти многообразия являются основными объектами изучения в комплексной геометрии . Одномерное комплексное многообразие называется римановой поверхностью . -мерное комплексное многообразие имеет размерность вещественного дифференцируемого многообразия. ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle n}$ ${\displaystyle 2n}$
• CR -многообразие — это многообразие, смоделированное на границах областей в . ${\displaystyle \mathbb {C} ^{n}}$
• «Бесконечномерные многообразия»: чтобы допустить бесконечные измерения, можно рассмотреть банаховы многообразия , которые локально гомеоморфны банаховым пространствам . Аналогично, многообразия Фреше локально гомеоморфны пространствам Фреше .
• Симплектическое многообразие — это разновидность многообразия, используемая для представления фазовых пространств в классической механике . Они наделены 2-формой , которая определяет скобку Пуассона . Близким типом многообразия является контактное многообразие .
• Комбинаторное многообразие — это разновидность многообразия, которая является дискретизацией многообразия. Обычно это кусочно-линейное многообразие, образованное симплициальными комплексами .
• Цифровое многообразие — это особый вид комбинаторного многообразия, который определен в цифровом пространстве. См. цифровую топологию .

Классификация и инварианты

Различные понятия многообразий имеют различные понятия классификации и инварианта; в этом разделе мы сосредоточимся на гладких замкнутых многообразиях.

Классификация гладких замкнутых многообразий в принципе хорошо понятна , за исключением размерности 4 : в низких размерностях (2 и 3) она геометрическая, через теорему об униформизации и решение гипотезы Пуанкаре , а в высоких размерностях (5 и выше) она алгебраическая, через теорию хирургии . Это классификация в принципе: общий вопрос о том, являются ли два гладких многообразия диффеоморфными, в общем случае невычислим. Кроме того, конкретные вычисления остаются сложными, и есть много открытых вопросов.

Ориентируемые поверхности можно визуализировать, а их классы диффеоморфизма перечислить по родам. Если даны две ориентируемые поверхности, можно определить, являются ли они диффеоморфными, вычислив их соответствующие роды и сравнив: они диффеоморфны тогда и только тогда, когда роды равны, поэтому род образует полный набор инвариантов .

В многомерных пространствах это сделать гораздо сложнее: многообразия более высоких измерений невозможно визуализировать напрямую (хотя визуальная интуиция полезна для их понимания), нельзя перечислить их классы диффеоморфизма, и вообще невозможно определить, относятся ли два различных описания многообразия более высоких измерений к одному и тому же объекту.

Однако можно определить, являются ли два многообразия разными , если есть некоторая внутренняя характеристика, которая их различает. Такие критерии обычно называют инвариантами , потому что, хотя они могут быть определены в терминах некоторого представления (например, рода в терминах триангуляции), они одинаковы относительно всех возможных описаний конкретного многообразия: они инвариантны при различных описаниях.

Можно было бы надеяться разработать арсенал инвариантных критериев, которые бы окончательно классифицировали все многообразия с точностью до изоморфизма. Известно, что для многообразий размерности 4 и выше не существует программы , которая могла бы решить, являются ли два многообразия диффеоморфными.

Гладкие многообразия имеют богатый набор инвариантов , происходящих из топологии точечных множеств , классической алгебраической топологии и геометрической топологии . Наиболее известными инвариантами, которые видны для поверхностей, являются ориентируемость (нормальный инвариант, также обнаруживаемый гомологией ) и род (гомологический инвариант).

Гладкие замкнутые многообразия не имеют локальных инвариантов (кроме размерности), хотя геометрические многообразия имеют локальные инварианты, в частности кривизну риманова многообразия и кручение многообразия, снабженного аффинной связностью . Это различие между локальными инвариантами и отсутствием локальных инвариантов является распространенным способом различения геометрии и топологии . Таким образом, все инварианты гладкого замкнутого многообразия являются глобальными.

Алгебраическая топология является источником ряда важных глобальных инвариантных свойств. Некоторые ключевые критерии включают свойство односвязности и ориентируемость (см. ниже). Действительно, несколько разделов математики, такие как гомология и теория гомотопии , а также теория характеристических классов были основаны для изучения инвариантных свойств многообразий.

Поверхности

Ориентируемость

В размерностях два и выше простым, но важным инвариантным критерием является вопрос о том, допускает ли многообразие осмысленную ориентацию. Рассмотрим топологическое многообразие с картами, отображающимися в . При наличии упорядоченного базиса для , карта заставляет свою часть многообразия приобрести чувство упорядоченности, которое в 3-мерном пространстве может рассматриваться как правостороннее или левостороннее. Перекрывающиеся карты не обязаны согласовываться в своем смысле упорядоченности, что дает многообразиям важную свободу. Для некоторых многообразий, таких как сфера, карты можно выбрать так, чтобы перекрывающиеся области согласовывались в своей «рукоятности»; это ориентируемые многообразия. Для других это невозможно. Последнюю возможность легко упустить из виду, поскольку любая замкнутая поверхность, вложенная (без самопересечения) в трехмерное пространство, является ориентируемой. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Вот несколько наглядных примеров неориентируемых многообразий: (1) лента Мёбиуса , которая является многообразием с границей, (2) бутылка Клейна , которая должна пересекать сама себя в своем трехмерном представлении, и (3) действительная проективная плоскость , которая естественным образом возникает в геометрии.

лента Мёбиуса

лента Мёбиуса

Начните с бесконечного кругового цилиндра, стоящего вертикально, многообразия без границы. Разрежьте его поперек вверху и внизу, чтобы получить две круговые границы, и цилиндрическую полосу между ними. Это ориентируемое многообразие с границей, на котором будет выполнена «хирургия». Разрежьте полосу так, чтобы она могла развернуться и стать прямоугольником, но держитесь за разрезанную часть. Поверните один конец на 180°, сделав внутреннюю поверхность обращенной наружу, и склейте концы обратно без швов. Это приведет к полосе с постоянным полуповоротом: лента Мёбиуса. Ее граница больше не является парой кругов, а (топологически) одним кругом; и то, что когда-то было ее «внутренней частью», слилось с ее «внешней частью», так что теперь у нее только одна сторона. Подобно бутылке Клейна ниже, эта двумерная поверхность должна пересекаться сама с собой в двух измерениях, но ее можно легко построить в трех или более измерениях.

Бутылка Клейна

Возьмите две ленты Мёбиуса; каждая имеет одну петлю в качестве границы. Выпрямите эти петли в круги и позвольте полоскам искривиться в перекрестные колпачки . Склеивание кругов вместе даст новое замкнутое многообразие без границы, бутылку Клейна. Закрытие поверхности никак не улучшает отсутствие ориентируемости, оно просто удаляет границу. Таким образом, бутылка Клейна является замкнутой поверхностью без различия между внутренней и внешней частью. В трехмерном пространстве поверхность бутылки Клейна должна проходить через себя. Построение бутылки Клейна, которая не является самопересекающейся, требует четырех или более измерений пространства.

Действительная проективная плоскость

Действительная проективная плоскость представляет собой двумерное многообразие, которое не может быть реализовано в трех измерениях без самопересечения, показанного здесь как поверхность Боя .

Начнем со сферы с центром в начале координат. Каждая линия, проходящая через начало координат, пронзает сферу в двух противоположных точках, называемых антиподами . Хотя физически это сделать невозможно, можно (рассмотрев факторпространство ) математически объединить каждую пару антиподов в одну точку. Полученная таким образом замкнутая поверхность является реальной проективной плоскостью, еще одной неориентируемой поверхностью. Она имеет ряд эквивалентных описаний и конструкций, но этот путь объясняет ее название: все точки на любой заданной прямой, проходящей через начало координат, проецируются в одну и ту же «точку» на этой «плоскости».

Род и характеристика Эйлера

Для двумерных многообразий ключевым инвариантным свойством является род , или «число ручек», присутствующих на поверхности. Тор — это сфера с одной ручкой, двойной тор — это сфера с двумя ручками и т. д. Действительно, можно полностью охарактеризовать компактные двумерные многообразия на основе рода и ориентируемости. В многообразиях более высокой размерности род заменяется понятием характеристики Эйлера , и в более общем смысле числами Бетти и гомологиями и когомологиями .

Карты многообразий

Поверхность Морена , погружение, используемое при выворачивании сферы

Так же, как существуют различные типы многообразий, существуют различные типы отображений многообразий . Помимо непрерывных функций и гладких функций в целом, существуют отображения со специальными свойствами. В геометрической топологии основным типом являются вложения , центральным примером которых является теория узлов , и обобщения, такие как погружения , субмерсии , накрывающие пространства и разветвленные накрывающие пространства . Основные результаты включают теорему Уитни о вложении и теорему Уитни о погружении .

В римановой геометрии можно потребовать отображения, сохраняющие риманову метрику, что приводит к понятиям изометрических вложений , изометрических погружений и римановых субмерсий ; основным результатом является теорема Нэша о вложении .

Скалярнозначные функции

3D-цветной график сферических гармоник степени ${\displaystyle n=5}$

Простейшим примером отображений между многообразиями являются скалярные функции на многообразии, или $${\displaystyle f\colon M\to \mathbb {R} }$$ $${\displaystyle f\colon M\to \mathbb {C} ,}$$

иногда называемые регулярными функциями или функционалами , по аналогии с алгебраической геометрией или линейной алгеброй. Они представляют интерес как сами по себе, так и для изучения лежащего в их основе многообразия.

В геометрической топологии наиболее часто изучаются функции Морса , которые дают разложения handlebody , в то время как в математическом анализе часто изучают решения уравнений с частными производными , важным примером которых является гармонический анализ , где изучаются гармонические функции : ядро ​​оператора Лапласа . Это приводит к таким функциям, как сферические гармоники , и к методам изучения многообразий с использованием теплового ядра , таким как прослушивание формы барабана и некоторые доказательства теоремы об индексе Атьи–Зингера .

Обобщения многообразий

Бесконечномерные многообразия

Определение многообразия можно обобщить, отказавшись от требования конечной размерности. Таким образом, бесконечномерное многообразие — это топологическое пространство, локально гомеоморфное топологическому векторному пространству над вещественными числами. Это исключает аксиомы точечного множества, допуская более высокие мощности и нехаусдорфовы многообразия ; и это исключает конечную размерность, позволяя моделировать такие структуры, как гильбертовы многообразия на гильбертовых пространствах , банаховы многообразия на банаховых пространствах и многообразия Фреше на пространствах Фреше . Обычно одно или другое условие ослабляют: многообразия с аксиомами точечного множества изучаются в общей топологии , в то время как бесконечномерные многообразия изучаются в функциональном анализе .

Орбифолды

Орбифолд — это обобщение многообразия, допускающее определенные виды « сингулярностей » в топологии. Грубо говоря, это пространство, которое локально выглядит как фактор некоторого простого пространства ( например, евклидова пространства) по действиям различных конечных групп . Сингулярности соответствуют неподвижным точкам действий группы, и действия должны быть совместимы в определенном смысле.

Алгебраические многообразия и схемы

Неособые алгебраические многообразия над действительными или комплексными числами являются многообразиями. Это обобщается, во-первых, путем разрешения особенностей, во-вторых, путем разрешения различных полей, и, в-третьих, путем эмуляции конструкции заплатки многообразий: так же, как многообразие склеивается из открытых подмножеств евклидова пространства, алгебраическое многообразие склеивается из аффинных алгебраических многообразий, которые являются нулевыми множествами многочленов над алгебраически замкнутыми полями. Схемы также склеиваются из аффинных схем, которые являются обобщением алгебраических многообразий. Обе связаны с многообразиями, но строятся алгебраически с использованием пучков вместо атласов.

Из-за особых точек многообразие в общем случае не является многообразием, хотя лингвистически французское variété , немецкое Mannigfaltigkeit и английское multiple во многом являются синонимами . Во французском языке алгебраическое многообразие называется une variété algébrique ( алгебраическое многообразие ), в то время как гладкое многообразие называется une variété différentielle ( дифференциальное многообразие ).

Стратифицированное пространство

«Стратифицированное пространство» — это пространство, которое можно разделить на части («страты»), где каждая страта является многообразием, а страты подгоняются друг к другу заданными способами (формально, фильтрация замкнутыми подмножествами). ^[8] Существуют различные технические определения, в частности, стратифицированное пространство Уитни (см. условия Уитни ) для гладких многообразий и топологически стратифицированное пространство для топологических многообразий. Основные примеры включают многообразие с границей (многообразие верхней размерности и граница коразмерности 1) и многообразия с углами (многообразие верхней размерности, граница коразмерности 1, углы коразмерности 2). Стратифицированные пространства Уитни представляют собой широкий класс пространств, включая алгебраические многообразия, аналитические многообразия, полуалгебраические множества и субаналитические множества .

CW-комплексы

Комплекс CW — это топологическое пространство, образованное склеиванием дисков разной размерности. В общем случае полученное пространство является сингулярным, следовательно, не является многообразием. Однако они представляют центральный интерес в алгебраической топологии, особенно в теории гомотопий .

Гомологические многообразия

Гомологическое многообразие — это пространство, которое ведет себя как многообразие с точки зрения теории гомологии. Это не все многообразия, но (в высокой размерности) их можно анализировать с помощью теории хирургии подобно многообразиям, а неспособность быть многообразием является локальным препятствием, как в теории хирургии. ^[9]

Дифференциальные пространства

Пусть будет непустым множеством. Предположим, что выбрано некоторое семейство действительных функций на . Обозначим его через . Это алгебра относительно поточечного сложения и умножения. Пусть будет снабжена топологией, индуцированной . Предположим также, что выполнены следующие условия. Во-первых: для каждого , где , и произвольного , композиция . Во-вторых: каждая функция , которая в каждой точке локально совпадает с некоторой функцией из , также принадлежит . Пара , для которой выполнены указанные выше условия, называется дифференциальным пространством Сикорского. ^[10] ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle C\subseteq \mathbb {R} ^{M}}$ ${\displaystyle M}$ ${\displaystyle C}$ ${\displaystyle H\in C^{\infty }\left(\mathbb {R} ^{n}\right)}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle f_{1},\dots ,f_{n}\in C}$ ${\displaystyle H\circ \left(f_{1},\dots ,f_{n}\right)\in C}$ ${\displaystyle M}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle (M,C)}$

Смотрите также

• Подмногообразие  — подмножество многообразия, которое само является многообразием; инъективное погружение в многообразие.
• Геодезическая  – Прямолинейный путь на искривленной поверхности или римановом многообразии.
• Направленная статистика  – Раздел статистики: статистика многообразий
• Список коллекторов
• Хронология многообразий  – Хронология математики
• Математика общей теории относительности

По размеру

• 3-многообразие  – Математическое пространство
• 4-многообразие  – Математическое пространство
• 5-многообразие  – Многообразие размерности пять
• Многообразия отображений  – локально выпуклые векторные пространства, удовлетворяющие очень мягкому условию полнотыPages displaying wikidata descriptions as a fallback

Примечания

1. Например, см. Риаза, Рикардо (2008), Дифференциально-алгебраические системы: аналитические аспекты и приложения схем, World Scientific, стр. 110, ISBN 9789812791818; Ганнинг, RC (1990), Введение в голоморфные функции нескольких переменных, том 2, CRC Press, стр. 73, ISBN 9780534133092.
2. Сигэюки Морита; Теруко Нагасе; Кацуми Номидзу (2001). Геометрия дифференциальных форм . Книжный магазин Американского математического общества. п. 12. ISBN 0-8218-1045-6.^{[ мертвая ссылка ]}
3. Понятие карты можно формализовать как разложение ячеек.
4. Пуанкаре, Х. (1895). «Анализ ситуации». Журнал Политехнической школы . Серия 11 (на французском языке). Готье-Виллар.
5. Арнольд, VI (1998). «О преподавании математики». Успехи мат. Наук (на русском языке). 53 (319): 229–234. дои : 10.4213/rm5 .; перевод на русский язык: Математические обзоры 53 (1998), № 1, 229–236
6. Уитни, Х. (1936). «Дифференцируемые многообразия». Annals of Mathematics . Вторая серия. 37 (3): 645–680. doi :10.2307/1968482. JSTOR  1968482.
7. Кервер, М. (1961). «Многообразие, которое не допускает никакой дифференцируемой структуры». Комментарий. Math. Helv. 35 (1): 1–14. doi :10.1007/BF02565940. S2CID  120977898.
8. Росс, Итан (2024-04-01). "Стратифицированные векторные расслоения: примеры и конструкции". Журнал геометрии и физики . 198 : 105114. arXiv : 2303.04200 . Bibcode : 2024JGP...19805114R. doi : 10.1016/j.geomphys.2024.105114. ISSN  0393-0440.
9. Брайант, Дж.; Ферри, С.; Мио, В.; Вайнбергер, С. (1996). «Топология гомологических многообразий». Annals of Mathematics . Вторая серия. 143 (3): 435–467. arXiv : math/9304210 . doi :10.2307/2118532. JSTOR  2118532.
10. Сикорский, Р. (1967). «Абстрактная ковариантная производная». Коллоквиум Математикум . 18 : 251–272. дои : 10,4064/см-18-1-251-272 .

Ссылки

• Фридман, Майкл Х. и Куинн, Фрэнк (1990) Топология 4-многообразий . Princeton University Press. ISBN 0-691-08577-3 . 
• Гийемен, Виктор и Поллак, Алан (1974) Дифференциальная топология . Prentice-Hall. ISBN 0-13-212605-2 . Продвинутый текст для студентов бакалавриата и магистратуры первого года обучения, вдохновленный Милнором. 
• Хемпель, Джон (1976) 3-многообразия . Издательство Принстонского университета. ISBN 0-8218-3695-1 . 
• Hirsch, Morris , (1997) Differential Topology . Springer Verlag. ISBN 0-387-90148-5 . Наиболее полное изложение с историческими экскурсами и превосходными, но сложными задачами. Стандартная справочная информация для тех, кто хочет глубоко разобраться в предмете. 
• Кирби, Робион К. и Зибенманн, Лоренс К. (1977) Основополагающие эссе о топологических многообразиях. Сглаживания и триангуляции . Издательство Принстонского университета. ISBN 0-691-08190-5 . Подробное исследование категории топологических многообразий. 
• Ли, Джон М. (2000) Введение в топологические многообразия . Springer-Verlag. ISBN 0-387-98759-2 . Подробный и всеобъемлющий текст для аспирантов первого года обучения. 
• Ли, Джон М. (2003) Введение в гладкие многообразия . Springer-Verlag. ISBN 0-387-95495-3 . Подробный и всеобъемлющий текст для аспирантов первого года обучения; продолжение Введения в топологические многообразия . 
• Мэсси, Уильям С. (1977) Алгебраическая топология: Введение . Springer-Verlag. ISBN 0-387-90271-6 . 
• Милнор, Джон (1997) Топология с дифференцируемой точки зрения . Princeton University Press. ISBN 0-691-04833-9 . Классическое краткое введение в дифференциальную топологию. 
• Манкрес, Джеймс Р. (1991) Анализ многообразий . Эддисон-Уэсли (перепечатано Westview Press) ISBN 0-201-51035-9 . Текст для студентов, посвященный многообразиям в .  ${\displaystyle \mathbb {R} ^{n}}$
• Манкрес, Джеймс Р. (2000) Топология . Prentice Hall. ISBN 0-13-181629-2 . 
• Neuwirth, LP, ed. (1975) Узлы, группы и 3-многообразия. Статьи, посвященные памяти Р. Х. Фокса . Princeton University Press. ISBN 978-0-691-08170-0 . 
• Риман, Бернхард , Gesammelte mathematische Werke und wissenschaftlicher Nachlass , Sändig Reprint. ISBN 3-253-03059-8 .  
  • Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse. Докторская диссертация 1851 года, в которой впервые появляется слово «многообразие» ( Mannigfaltigkeit ).
  • Ueber die Hypothesen, welche der Geometrie zu Grunde Ligen. Инаугурационная лекция в Геттингене 1854 года ( Habilitationsschrift ).
• Спивак, Майкл (1965) Исчисление на многообразиях: современный подход к классическим теоремам продвинутого исчисления . WA Benjamin Inc. (переиздано Addison-Wesley и Westview Press). ISBN 0-8053-9021-9 . Знаменитый краткий текст для студентов бакалавриата и магистратуры первого года обучения. 
• Спивак, Майкл (1999) Всестороннее введение в дифференциальную геометрию (3-е издание) Опубликовано Perish Inc. Энциклопедическая серия из пяти томов, представляющая систематическое рассмотрение теории многообразий, римановой геометрии, классической дифференциальной геометрии и множества других тем для аспирантов первого и второго года обучения.
• Ту, Лоринг В. (2011). Введение в многообразия (2-е изд.). Нью-Йорк: Springer. ISBN 978-1-4419-7399-3.. Краткий текст для выпускников первого года обучения.

Внешние ссылки

• «Многообразие», Энциклопедия математики , EMS Press , 2001 [1994]
• Dimensions-math.org (Фильм, объясняющий и визуализирующий многообразия вплоть до четвертого измерения.)
• Проект атласа многообразий Института математики Макса Планка в Бонне