Реальное координатное пространство

Пространство, образованное n -кортежами действительных чисел

Декартовы координаты идентифицируют точки евклидовой плоскости с парами действительных чисел.

В математике действительное координатное пространство или действительное координатное n -пространство размерности n , обозначаемое Rn или , представляет собой набор всех упорядоченных n -кортежей действительных чисел , то есть набор всех последовательностей из n действительных чисел, также известный ^как как координатные векторы . Особые ^случаи называются вещественной линией R1 , вещественной координатной плоскостью ^R2 и вещественным координатным трехмерным пространством R3 ^. Благодаря покомпонентному сложению и скалярному умножению это настоящее векторное пространство . ${\displaystyle \mathbb {R} ^{n}}$

Координаты над любым базисом элементов реального векторного пространства образуют действительное координатное пространство той же размерности , что и векторное пространство. Аналогично, декартовы координаты точек евклидова пространства размерности n , En ⁽ евклидова линия , E ; евклидова плоскость , E ² ; евклидово трёхмерное пространство , E ³ ) образуют вещественное координатное пространство размерности n .

Эти однозначные соответствия между векторами, точками и векторами координат объясняют названия координатного пространства и координатного вектора . Это позволяет использовать геометрические термины и методы для изучения реальных координатных пространств и, наоборот, использовать методы исчисления в геометрии. Этот подход к геометрии был предложен Рене Декартом в 17 веке. Он широко используется, поскольку позволяет находить точки в евклидовых пространствах и выполнять вычисления с ними.

Определение и структуры

Для любого натурального числа ⁿ множество Rn состоит из всех n - наборов действительных чисел ( R ) . Его называют « n -мерным реальным пространством» или «реальным n -пространством».

Таким образом, элемент R ⁿ представляет собой n -кортеж и записывается

$${\displaystyle (x_{1},x_{2},\ldots ,x_{n})}$$

x _iисчислении многих переменныхфункции нескольких действительных переменных ивекторной функцииподмножестваминекоторого ⁿ

Реальное n -пространство имеет еще несколько свойств, в частности:

• С покомпонентным сложением и скалярным умножением это настоящее векторное пространство . Каждое n -мерное вещественное векторное пространство изоморфно ему.
• Со скалярным произведением (сумма почленных произведений компонентов) это пространство внутреннего продукта . Каждое n -мерное реальное пространство внутреннего продукта изоморфно ему.
• Как и любое пространство внутреннего продукта, это топологическое пространство и топологическое векторное пространство .
• Это евклидово пространство и вещественное аффинное пространство , и каждое евклидово или аффинное пространство изоморфно ему.
• Это аналитическое многообразие , и ^его можно рассматривать как прототип всех многообразий , поскольку по определению многообразие вблизи каждой точки изоморфно открытому подмножеству Rn .
• Это алгебраическое многообразие , и каждое вещественное алгебраическое многообразие ^{является} подмножеством Rn .

Эти свойства и структуры Rn делают его фундаментальным практически во всех областях математики и областях их применения, таких как ^{статистика} , теория вероятностей и многие разделы физики .

Область определения функции нескольких переменных

Любую функцию f ( x ₁ ,  x ₂ , ...,  x _n ) от n действительных переменных можно рассматривать как функцию на R ⁿ (то есть с R ⁿ в качестве области определения ). Использование реального n -пространства вместо нескольких переменных, рассматриваемых отдельно, может упростить обозначения и предложить разумные определения. Рассмотрим для n = 2 функциональную композицию следующего вида:

$${\displaystyle F(t)=f(g_{1}(t),g_{2}(t)),}$$

функции g1g2_{_ _}

• ∀ x ₁  ∈  R  : f ( x ₁ , ·) непрерывно (по x ₂ )
• ∀ x ₂  ∈  R  : f (·,  x ₂ ) непрерывен (по x ₁ )

тогда F не обязательно непрерывен. Непрерывность — более сильное условие: непрерывность f в естественной топологии R ² (обсуждаемой ниже), также называемой непрерывностью многих переменных , которая достаточна для непрерывности композиции F .

Векторное пространство

Координатное пространство ^Rn образует n - мерное векторное пространство над полем действительных чисел с добавлением структуры ^{линейности} и часто до сих пор обозначается Rn . Операции над R ⁿ как векторным пространством обычно определяются формулой

$${\displaystyle \mathbf {x} +\mathbf {y} =(x_{1}+y_{1},x_{2}+y_{2},\ldots ,x_{n}+y_{n})}$$

$${\displaystyle \alpha \mathbf {x} =(\alpha x_{1},\alpha x_{2},\ldots ,\alpha x_{n}).}$$

вектор

$${\displaystyle \mathbf {0} =(0,0,\ldots ,0)}$$

аддитивный обратныйx

$${\displaystyle -\mathbf {x} =(-x_{1},-x_{2},\ldots ,-x_{n}).}$$

Эта структура важна, поскольку любое ⁿ - мерное вещественное векторное пространство изоморфно векторному пространству Rn .

Матричное обозначение

В стандартной матричной записи каждый элемент R ⁿ обычно записывается как вектор-столбец.

$${\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}}}$$

вектор-строку

$${\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\cdots &x_{n}\end{bmatrix}}.}$$

Координатное пространство R ⁿ тогда можно интерпретировать как пространство всех векторов-столбцов размера n  × 1 или всех векторов-строк размера 1 ×  n с обычными матричными операциями сложения и скалярного умножения .

Линейные преобразования из R ⁿ в R ^m можно тогда записать в виде матриц размера m  ×  n , которые действуют на элементы R ⁿ посредством левого умножения (когда элементы R ⁿ являются вектор-столбцами) и на элементы R ^m посредством правого умножения (когда они являются векторами-строками). Формула умножения слева, частного случая матричного умножения , выглядит следующим образом:

$${\displaystyle (A{\mathbf {x} })_{k}=\sum _{l=1}^{n}A_{kl}x_{l}}$$

Любое линейное преобразование является непрерывной функцией (см. ниже). Кроме того, матрица определяет открытое отображение из Rn в Rm тогда и только тогда, ^{когда ранг} матрицы равен m .

Стандартная основа

Координатное пространство R ⁿ имеет стандартную основу:

$${\displaystyle {\begin{aligned}\mathbf {e} _{1}&=(1,0,\ldots ,0)\\\mathbf {e} _{2}&=(0,1,\ldots ,0)\\&{}\;\;\vdots \\\mathbf {e} _{n}&=(0,0,\ldots ,1)\end{aligned}}}$$

Чтобы убедиться в том, что это базис, заметим, что произвольный вектор из ^Rn можно однозначно записать в виде

$${\displaystyle \mathbf {x} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}.}$$

Геометрические свойства и использование

Ориентация

Тот факт, что действительные числа , в отличие от многих других полей , составляют упорядоченное поле ^, приводит к структуре ориентации на Rn . Любое линейное отображение R ⁿ полного ранга в себя либо сохраняет, либо меняет ориентацию пространства в зависимости от знака определителя его матрицы . Если переставить координаты (или, другими словами, элементы базиса), то результирующая ориентация будет зависеть от четности перестановки .

Диффеоморфизмы R ⁿ или областей в нем , в силу того , что они избегают нулевого якобиана , также классифицируются как сохраняющие ориентацию и меняющие ориентацию. Это имеет важные последствия для теории дифференциальных форм , приложения которой включают электродинамику .

Другое проявление этой структуры состоит в том, что ^{точечное} отражение в Rn имеет разные свойства в зависимости от четности n . Для четного n он сохраняет ориентацию, а для нечетного n меняется на обратную (см. также неправильное вращение ).

Аффинное пространство

R ^n, понимаемый как аффинное пространство, представляет собой то же самое пространство, где R ⁿ как векторное пространство действует посредством сдвигов . И наоборот, вектор следует понимать как « разницу между двумя точками», обычно иллюстрируемую направленным отрезком линии , соединяющим две точки. Это различие гласит, что не существует канонического выбора места начала координат в аффинном n -пространстве, поскольку его можно перевести куда угодно.

Выпуклость

n -симплекс (см. ниже) — это стандартное выпуклое множество, которое отображается в каждый многогранник и является пересечением стандартной ( n + 1) аффинной гиперплоскости (стандартного аффинного пространства) и стандартного ( n + 1) ортанта (стандартного аффинного пространства). конус).

В реальном векторном пространстве, таком как ^Rn , можно определить выпуклый конус , который содержит все неотрицательные линейные комбинации своих векторов. Соответствующее понятие в аффинном пространстве — это выпуклое множество , которое допускает только выпуклые комбинации (неотрицательные линейные комбинации, сумма которых равна 1).

На языке универсальной алгебры векторное пространство — это алгебра над универсальным векторным пространством R ^∞ конечных последовательностей коэффициентов, соответствующих конечным суммам векторов, а аффинное пространство — это алгебра над универсальной аффинной гиперплоскостью в этом пространстве (из конечные последовательности, суммирующиеся с 1), конус — алгебра над универсальным ортантом (конечных последовательностей неотрицательных чисел), а выпуклое множество — алгебра над универсальным симплексом (конечных последовательностей неотрицательных чисел, суммирующихся с 1). Это геометризирует аксиомы в терминах «сумм с (возможными) ограничениями на координаты».

Другая концепция выпуклого анализа - это выпуклая функция от R ⁿ до действительных чисел, которая определяется через неравенство между ее значением в выпуклой комбинации точек и суммой значений в этих точках с одинаковыми коэффициентами.

Евклидово пространство

Скалярное произведение

$${\displaystyle \mathbf {x} \cdot \mathbf {y} =\sum _{i=1}^{n}x_{i}y_{i}=x_{1}y_{1}+x_{2}y_{2}+\cdots +x_{n}y_{n}}$$

норму | х | знак равно √ Икс ⋅ ИксR ⁿевклидову норму

$${\displaystyle d(\mathbf {x} ,\mathbf {y} )=\|\mathbf {x} -\mathbf {y} \|={\sqrt {\sum _{i=1}^{n}(x_{i}-y_{i})^{2}}}}$$

метрического пространстваR ⁿ

Что касается структуры векторного пространства, то обычно предполагается, что скалярное произведение и евклидово расстояние существуют в R ⁿ без особых объяснений. Однако реальное n -пространство и евклидово n -пространство, строго говоря, являются разными объектами. Любое евклидово n -пространство имеет систему координат , в которой скалярное произведение и евклидово расстояние имеют показанную выше форму, называемую декартовой . Но в евклидовом пространстве существует множество декартовых систем координат.

И наоборот, приведенная выше формула для евклидовой метрики определяет стандартную евклидову структуру на R ⁿ , но она не является единственно возможной. На самом деле, любая положительно определенная квадратичная форма q определяет свое собственное «расстояние» √ q ( x − y ) , но оно не сильно отличается от евклидовой в том смысле, что

$${\displaystyle \exists C_{1}>0,\ \exists C_{2}>0,\ \forall \mathbf {x} ,\mathbf {y} \in \mathbb {R} ^{n}:C_{1}d(\mathbf {x} ,\mathbf {y} )\leq {\sqrt {q(\mathbf {x} -\mathbf {y} )}}\leq C_{2}d(\mathbf {x} ,\mathbf {y} ).}$$

метрическим пространствомR ⁿаффинное преобразованиеC ₂1 /  C ₁^{[ нужны разъяснения ]}

Вышеупомянутая эквивалентность метрических функций остается в силе, если √ q ( x - y ) заменяется на M ( x - y ) , где M - любая выпуклая положительная однородная функция степени 1, т.е. векторная норма (полезные примеры см. в разделе «Расстояние Минковского »). . В силу того, что любая «естественная» метрика на Rn особо не отличается от евклидовой метрики, Rn не ^всегда отличается от евклидова n -пространства даже в профессиональных математических работах ^.

В алгебраической и дифференциальной геометрии

Хотя определение многообразия не требует, чтобы его модельное пространство было Rn , этот выбор является наиболее распространенным и почти исключительным в ^{дифференциальной} геометрии .

С другой стороны, теоремы вложения Уитни утверждают, что любое вещественное дифференцируемое m -мерное многообразие можно вложить в R ^{2 m} .

Другие выступления

Другие структуры, рассматриваемые на Rn ^, включают структуру псевдоевклидова пространства , симплектическую структуру (четное n ) и контактную структуру (нечетное n ). Все эти структуры, хотя и могут быть определены бескоординатным способом, допускают стандартные (и достаточно простые) формы в координатах.

Rn также является действительным векторным подпространством Cn ^, которое инвариантно относительно комплексного ^{сопряжения} ; см. также усложнение .

Многогранники в R n

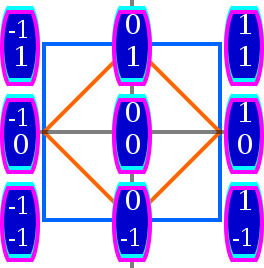
Существует три семейства многогранников , которые имеют простые представления в пространствах R ⁿ для любого n и могут использоваться для визуализации любой аффинной системы координат в реальном n -пространстве. Вершины гиперкуба имеют координаты ( x ₁ ,  x ₂ , ...,  x _n ) , где каждый x _k принимает одно из двух значений, обычно 0 или 1. Однако вместо 0 и 1 можно выбрать любые два числа. , например -1 и 1. n -гиперкуб можно рассматривать как декартово произведение n одинаковых интервалов (таких как единичный интервал [0,1] ) на действительной прямой. Как n - мерное подмножество его можно описать системой из 2n неравенств :

$${\displaystyle {\begin{matrix}0\leq x_{1}\leq 1\\\vdots \\0\leq x_{n}\leq 1\end{matrix}}}$$

[0,1]

$${\displaystyle {\begin{matrix}|x_{1}|\leq 1\\\vdots \\|x_{n}|\leq 1\end{matrix}}}$$

[−1,1]

Каждая вершина перекрестного многогранника имеет для некоторого k координату x _k , равную ±1, а все остальные координаты равны 0 (так что это k -й стандартный базисный вектор с точностью до знака ). Это двойственный многогранник гиперкуба. Как n -мерное подмножество его можно описать одним неравенством, которое использует операцию абсолютного значения :

$${\displaystyle \sum _{k=1}^{n}|x_{k}|\leq 1\,,}$$

2n линейных неравенств ^.

Третий многогранник с просто перечислимыми координатами — это стандартный симплекс , вершинами которого являются n стандартных базисных векторов и начало координат (0, 0, ..., 0) . Как n -мерное подмножество оно описывается системой из n + 1 линейных неравенств:

$${\displaystyle {\begin{matrix}0\leq x_{1}\\\vdots \\0\leq x_{n}\\\sum \limits _{k=1}^{n}x_{k}\leq 1\end{matrix}}}$$

Топологические свойства

Топологическую структуру R n (называемую стандартной топологией , ^{евклидовой} топологией или обычной топологией ) можно получить не только из декартова произведения. Она также идентична естественной топологии, индуцированной евклидовой метрикой, обсуждавшейся выше: множество открыто в евклидовой топологии тогда и только тогда, когда оно содержит открытый шар вокруг каждой из своих точек. Кроме того, Rn — линейное топологическое пространство (см. непрерывность линейных отображений выше), и существует только одна возможная (нетривиальная) топология, совместимая с его линейной структурой ^. Поскольку существует множество открытых линейных отображений Rn в себя, которые не являются ^{изометриями} , на Rn может существовать множество евклидовых структур ^, соответствующих одной и той же топологии. ^{На самом деле} оно мало зависит даже от линейной структуры: существует множество нелинейных диффеоморфизмов (и других гомеоморфизмов) Rn на самого себя или его части, такие как евклидов открытый шар или внутренность гиперкуба).

R ⁿ имеет топологическую размерность n .

Важным и далеко не поверхностным результатом по топологии Rn является ^{инвариантность} области определения Брауэра . Любое подмножество Rn (с его топологией подпространства ), которое гомеоморфно другому открытому подмножеству Rn ^{, само по себе} является открытым. Непосредственным следствием этого является то, что R ^m не гомеоморфен R n ^, если m ≠ n – интуитивно «очевидный» результат, который, тем не менее, трудно доказать.

Несмотря на разницу в топологическом измерении и вопреки наивному восприятию, можно непрерывно и сюръективно отображать меньшее размерное ^{[ необходимо разъяснение ]} реальное пространство на R ⁿ . Возможна непрерывная (хотя и не гладкая) кривая, заполняющая пространство (образ R ^{1 ). [ нужны разъяснения ]}

Примеры

п ≤ 1

Случаи 0 ≤ n ≤ 1 не предлагают ничего нового: R ¹ — это действительная линия , тогда как R ⁰ (пространство, содержащее пустой вектор-столбец) — это одноэлементное пространство , понимаемое как нулевое векторное пространство . Однако полезно включить их как тривиальные случаи теорий, описывающих разные n .

п = 2

И гиперкуб, и кросс-многогранник в R ² являются квадратами , но координаты вершин расположены по-разному.

Случай ( x,y ), где x и y — действительные числа , был разработан как декартова плоскость P. Дальнейшая структура была добавлена ​​с помощью евклидовых векторов , представляющих направленные отрезки прямой в P . Плоскость также была разработана как расширение поля путем добавления корней X ² + 1 = 0 к реальному полю. Корень i действует на P как четверть оборота с ориентацией против часовой стрелки. Этот корень порождает группу . Когда ( x,y ) пишется x + y i, это комплексное число . ${\displaystyle \mathbf {C} }$ ${\displaystyle \mathbf {R} .}$ ${\displaystyle \{i,-1,-i,+1\}\equiv \mathbf {Z} /4\mathbf {Z} }$

Другое групповое действие , где актер выражен как j, использует линию y = x для инволюции переворота плоскости ( x,y ) ↦ ( y,x ), обмена координатами. В этом случае точки P записываются x + y j и называются расщепляемыми комплексными числами . Эти числа при покоординатном сложении и умножении по jj =+1 образуют кольцо , не являющееся полем. ${\displaystyle \mathbf {Z} /2\mathbf {Z} }$

Другая кольцевая структура на P использует нильпотентную e для записи x + ye вместо ( x,y ). Действие e на P сводит плоскость к прямой: ее можно разложить на проекцию на координату x, затем повернув результат на четверть к оси y: e ( x + y e) = x e, поскольку e ² = 0. Число x + y e является двойственным числом . Двойственные числа образуют кольцо, но, поскольку e не имеет мультипликативного обратного, оно не порождает группу, поэтому действие не является групповым действием.

Исключение (0,0) из P создает проективные координаты [ x  : y ] , которые описывают реальную проективную линию, одномерное пространство. Поскольку начало координат исключено, существует хотя бы одно из отношений x / y и y / x . Тогда [ x  : y ] = [ x / y  :1] или [ x  : y ] = [1: y / x ]. Проективная прямая P1 ( R ) представляет собой топологическое многообразие , покрытое двумя координатными картами , [ z  :1] → ^z или [1: z ] → z , которые образуют атлас . Для точек, покрытых обеими картами, функция перехода представляет собой мультипликативную инверсию в открытой окрестности точки, что обеспечивает требуемый гомеоморфизм в многообразии. Одно из применений вещественной проективной прямой можно найти в метрической геометрии Кэли – Клейна .

п = 3

Куб (гиперкуб) и октаэдр (перекрестный многогранник) R ³ . Координаты не показаны

п = 4

R ⁴ можно представить, используя тот факт, что 16 точек ( x ₁ ,  x ₂ ,  x ₃ ,  x ₄ ) , где каждая x _k равна либо 0, либо 1, являются вершинами тессеракта ( на рисунке), 4-гиперкуба (см. выше).

Первое крупное использование R ⁴ — это модель пространства-времени : три пространственные координаты плюс одна временная . Обычно это связывают с теорией относительности , хотя со времен Галилея для таких моделей использовались четыре измерения . Однако выбор теории приводит к другой структуре: в теории относительности Галилея координата t является привилегированной, а в теории относительности Эйнштейна — нет. Действие специальной теории относительности происходит в пространстве Минковского . Общая теория относительности использует искривленные пространства, которые для большинства практических целей можно рассматривать как R ⁴ с искривленной метрикой . Ни одна из этих структур не обеспечивает (положительно определенную ⁾ метрику R 4 .

Евклидово R ⁴ также привлекает внимание математиков, например, из-за его связи с кватернионами , которые сами по себе являются 4-мерной реальной алгеброй . Дополнительную информацию см. вращении в 4-мерном евклидовом пространстве .

В дифференциальной геометрии n = 4 — единственный случай, когда R ⁿ допускает нестандартную дифференциальную структуру : см. экзотический R ⁴ .

Нормы по Р н

Можно определить множество норм в ^{векторном} пространстве Rn . Некоторые распространенные примеры:

• p -норма , определяемая для всех где – положительное целое число. Случай очень важный, потому что это именно евклидова норма . ${\textstyle \|\mathbf {x} \|_{p}:={\sqrt[{p}]{\sum _{i=1}^{n}|x_{i}|^{p}}}}$ ${\displaystyle \mathbf {x} \in \mathbf {R} ^{n}}$ ${\displaystyle p}$ ${\displaystyle p=2}$
• -норма или максимальная норма , определенная для всех . Это предел всех p-норм : . ${\displaystyle \infty }$ ${\displaystyle \|\mathbf {x} \|_{\infty }:=\max\{x_{1},\dots ,x_{n}\}}$ ${\displaystyle \mathbf {x} \in \mathbf {R} ^{n}}$ ${\textstyle \|\mathbf {x} \|_{\infty }=\lim _{p\to \infty }{\sqrt[{p}]{\sum _{i=1}^{n}|x_{i}|^{p}}}}$

Действительно удивительный и полезный результат состоит в том, что каждая норма, определенная на Rn ^, эквивалентна . Это означает, что для двух произвольных норм и на R ⁿ всегда можно найти положительные действительные числа такие, что ${\displaystyle \|\cdot \|}$ ${\displaystyle \|\cdot \|'}$ ${\displaystyle \alpha ,\beta >0}$

$${\displaystyle \alpha \cdot \|\mathbf {x} \|\leq \|\mathbf {x} \|'\leq \beta \cdot \|\mathbf {x} \|}$$

${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$

Это определяет отношение эквивалентности на множестве всех норм ^на Rn . С помощью этого результата вы можете проверить, что последовательность векторов в R ⁿ сходится с тогда и только тогда, когда она сходится с . ${\displaystyle \|\cdot \|}$ ${\displaystyle \|\cdot \|'}$

Вот набросок того, как может выглядеть доказательство этого результата:

Ввиду отношения эквивалентности достаточно показать, что каждая норма на R ⁿ эквивалентна евклидовой норме . Пусть – произвольная норма ^на Rn . Доказательство разделено на два этапа: ${\displaystyle \|\cdot \|_{2}}$ ${\displaystyle \|\cdot \|}$

• Покажем, что существует такое , что для всех . На этом этапе вы используете тот факт, что каждый может быть представлен как линейная комбинация стандартного базиса : . Тогда с учетом неравенства Коши–Шварца ${\displaystyle \beta >0}$ ${\displaystyle \|\mathbf {x} \|\leq \beta \cdot \|\mathbf {x} \|_{2}}$ ${\displaystyle \mathbf {x} \in \mathbf {R} ^{n}}$ ${\displaystyle \mathbf {x} =(x_{1},\dots ,x_{n})\in \mathbf {R} ^{n}}$ ${\textstyle \mathbf {x} =\sum _{i=1}^{n}e_{i}\cdot x_{i}}$
  $${\displaystyle \|\mathbf {x} \|=\left\|\sum _{i=1}^{n}e_{i}\cdot x_{i}\right\|\leq \sum _{i=1}^{n}\|e_{i}\|\cdot |x_{i}|\leq {\sqrt {\sum _{i=1}^{n}\|e_{i}\|^{2}}}\cdot {\sqrt {\sum _{i=1}^{n}|x_{i}|^{2}}}=\beta \cdot \|\mathbf {x} \|_{2},}$$
  где . ${\textstyle \beta :={\sqrt {\sum _{i=1}^{n}\|e_{i}\|^{2}}}}$
• Теперь нам предстоит найти такое , чтобы для всех . Предположим, такого нет . Тогда для любого a существует такое, что . Определите вторую последовательность с помощью . Эта последовательность ограничена, поскольку . Итак, согласно теореме Больцано–Вейерштрасса существует сходящаяся подпоследовательность с пределом R ⁿ . Теперь мы покажем, что но , что является противоречием. Это ${\displaystyle \alpha >0}$ ${\displaystyle \alpha \cdot \|\mathbf {x} \|_{2}\leq \|\mathbf {x} \|}$ ${\displaystyle \mathbf {x} \in \mathbf {R} ^{n}}$ ${\displaystyle \alpha }$ ${\displaystyle k\in \mathbf {N} }$ ${\displaystyle \mathbf {x} _{k}\in \mathbf {R} ^{n}}$ ${\displaystyle \|\mathbf {x} _{k}\|_{2}>k\cdot \|\mathbf {x} _{k}\|}$ ${\displaystyle ({\tilde {\mathbf {x} }}_{k})_{k\in \mathbf {N} }}$ ${\textstyle {\tilde {\mathbf {x} }}_{k}:={\frac {\mathbf {x} _{k}}{\|\mathbf {x} _{k}\|_{2}}}}$ ${\displaystyle \|{\tilde {\mathbf {x} }}_{k}\|_{2}=1}$ ${\displaystyle ({\tilde {\mathbf {x} }}_{k_{j}})_{j\in \mathbf {N} }}$ ${\displaystyle \mathbf {a} \in }$ ${\displaystyle \|\mathbf {a} \|_{2}=1}$ ${\displaystyle \mathbf {a} =\mathbf {0} }$
  $${\displaystyle \|\mathbf {a} \|\leq \left\|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\right\|+\left\|{\tilde {\mathbf {x} }}_{k_{j}}\right\|\leq \beta \cdot \left\|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\right\|_{2}+{\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}\ {\overset {j\to \infty }{\longrightarrow }}\ 0,}$$
  потому что и , так . Это подразумевает , так что . С другой стороны , потому что . Это не может быть правдой, поэтому предположение было ложным и такое существует . ${\displaystyle \|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\|\to 0}$ ${\displaystyle 0\leq {\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}<{\frac {1}{k_{j}}}}$ ${\displaystyle {\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}\to 0}$ ${\displaystyle \|\mathbf {a} \|=0}$ ${\displaystyle \mathbf {a} =\mathbf {0} }$ ${\displaystyle \|\mathbf {a} \|_{2}=1}$ ${\displaystyle \|\mathbf {a} \|_{2}=\left\|\lim _{j\to \infty }{\tilde {\mathbf {x} }}_{k_{j}}\right\|_{2}=\lim _{j\to \infty }\left\|{\tilde {\mathbf {x} }}_{k_{j}}\right\|_{2}=1}$ ${\displaystyle \alpha >0}$

Смотрите также

• Экспоненциальный объект для теоретического объяснения надстрочной записи.
• Геометрическое пространство
• Реальное проективное пространство

Источники

• Келли, Джон Л. (1975). Общая топология . Спрингер-Верлаг. ISBN 0-387-90125-6.
• Манкрес, Джеймс (1999). Топология . Прентис-Холл. ISBN 0-13-181629-2.