Волна

Повторяющиеся колебания около равновесия

Поверхностные волны на воде, показывающие водную рябь

В физике , математике , инженерии и смежных областях волна — это распространяющееся динамическое возмущение (изменение от равновесия ) одной или нескольких величин . Периодические волны многократно колеблются около равновесного (покоящегося) значения с некоторой частотой . Когда вся форма волны движется в одном направлении, говорят, что это бегущая волна ; напротив, пара наложенных периодических волн, движущихся в противоположных направлениях, создает стоячую волну . В стоячей волне амплитуда вибрации имеет нули в некоторых положениях, где амплитуда волны кажется меньшей или даже нулевой.

В классической физике чаще всего изучаются два типа волн : механические волны и электромагнитные волны . В механической волне поля напряжений и деформаций колеблются около механического равновесия. Механическая волна — это локальная деформация (напряжение) в некоторой физической среде, которая распространяется от частицы к частице, создавая локальные напряжения , которые также вызывают напряжение в соседних частицах. Например, звуковые волны — это вариации локального давления и движения частиц , которые распространяются через среду. Другими примерами механических волн являются сейсмические волны , гравитационные волны , поверхностные волны и колебания струн . В электромагнитной волне (например, световой) связь между электрическими и магнитными полями поддерживает распространение волн, включающих эти поля, в соответствии с уравнениями Максвелла . Электромагнитные волны могут распространяться через вакуум и через некоторые диэлектрические среды (на длинах волн, где они считаются прозрачными ). Электромагнитные волны, определяемые их частотами (или длинами волн ), имеют более конкретные обозначения, включая радиоволны , инфракрасное излучение , терагерцовые волны , видимый свет , ультрафиолетовое излучение , рентгеновские лучи и гамма-лучи .

Другие типы волн включают гравитационные волны , которые являются возмущениями в пространстве-времени , которые распространяются согласно общей теории относительности ; тепловые диффузионные волны ; плазменные волны , которые объединяют механические деформации и электромагнитные поля; реакционно-диффузионные волны , такие как в реакции Белоусова-Жаботинского ; и многие другие. Механические и электромагнитные волны переносят энергию , ^[1] импульс и информацию , но они не переносят частицы в среде. В математике и электронике волны изучаются как сигналы . ^[2] С другой стороны, некоторые волны имеют огибающие , которые вообще не движутся, такие как стоячие волны (которые являются основополагающими для музыки) и гидравлические скачки .

Пример распространения биологических волн по коре головного мозга, пример распространения деполяризации . ^[3]

Физическое волновое поле почти всегда ограничено некоторой конечной областью пространства, называемой его доменом . Например, сейсмические волны, генерируемые землетрясениями, значимы только внутри и на поверхности планеты, поэтому их можно игнорировать за ее пределами. Однако волны с бесконечным доменом, которые простираются на все пространство, обычно изучаются в математике и являются очень ценными инструментами для понимания физических волн в конечных областях.

Плоская волна — важная математическая идеализация, в которой возмущение одинаково вдоль любой (бесконечной) плоскости, перпендикулярной определенному направлению движения. Математически простейшей волной является синусоидальная плоская волна , в которой в любой точке поле испытывает простое гармоническое движение на одной частоте. В линейных средах сложные волны, как правило, можно разложить как сумму многих синусоидальных плоских волн, имеющих разные направления распространения и/или разные частоты . Плоская волна классифицируется как поперечная волна , если возмущение поля в каждой точке описывается вектором, перпендикулярным направлению распространения (также направлению передачи энергии); или продольная волна , если эти векторы выровнены с направлением распространения. Механические волны включают как поперечные, так и продольные волны; с другой стороны, электромагнитные плоские волны являются строго поперечными, в то время как звуковые волны в жидкостях (например, в воздухе) могут быть только продольными. Это физическое направление колеблющегося поля относительно направления распространения также называется поляризацией волны , что может быть важным атрибутом.

Математическое описание

Одиночные волны

Волну можно описать так же, как поле, а именно как функцию, где — положение, а — время. ${\displaystyle F(x,t)}$ ${\displaystyle x}$ ${\displaystyle t}$

Значение является точкой пространства, в частности, в области, где определена волна. В математических терминах это обычно вектор в декартовом трехмерном пространстве . Однако во многих случаях можно игнорировать одно измерение и позволить быть точкой декартовой плоскости . Так обстоит дело, например, при изучении колебаний кожи барабана. Можно даже ограничиться точкой декартовой линии – то есть множеством действительных чисел . Так обстоит дело, например, при изучении колебаний струны скрипки или блокфлейты . Время , с другой стороны, всегда предполагается скаляром ; то есть действительным числом. ${\displaystyle x}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle x}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle x}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle t}$

Значение может быть любой физической величиной, назначенной точке , которая может меняться со временем. Например, если представляет колебания внутри упругого твердого тела, значение обычно является вектором, который дает текущее смещение от материальных частиц, которые находились бы в точке при отсутствии вибрации. Для электромагнитной волны значение может быть вектором электрического поля или вектором магнитного поля или любой связанной величиной, такой как вектор Пойнтинга . В динамике жидкости значение может быть вектором скорости жидкости в точке или любым скалярным свойством, таким как давление , температура или плотность . В химической реакции может быть концентрацией некоторого вещества в окрестности точки реакционной среды. ${\displaystyle F(x,t)}$ ${\displaystyle x}$ ${\displaystyle F}$ ${\displaystyle F(x,t)}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle F}$ ${\displaystyle E}$ ${\displaystyle H}$ ${\displaystyle E\times H}$ ${\displaystyle F(x,t)}$ ${\displaystyle x}$ ${\displaystyle F(x,t)}$ ${\displaystyle x}$

Для любого измерения (1, 2 или 3) область определения волны является подмножеством , таким образом, что значение функции определено для любой точки в . Например, при описании движения кожи барабана можно рассматривать как диск (круг) на плоскости с центром в начале координат , и пусть будет вертикальным смещением кожи в точке и в момент времени . ${\displaystyle d}$ ${\displaystyle D}$ ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle F(x,t)}$ ${\displaystyle x}$ ${\displaystyle D}$ ${\displaystyle D}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle (0,0)}$ ${\displaystyle F(x,t)}$ ${\displaystyle x}$ ${\displaystyle D}$ ${\displaystyle t}$

Суперпозиция

Волны одного типа часто накладываются друг на друга и встречаются одновременно в заданной точке пространства и времени. Свойства в этой точке являются суммой свойств каждой составляющей волны в этой точке. В общем случае скорости не одинаковы, поэтому форма волны будет меняться со временем и пространством.

Спектр волн

Семьи волн

Иногда интерес представляет одна конкретная волна. Однако чаще всего нужно понимать большой набор возможных волн; например, все способы, которыми может вибрировать кожа барабана после удара по ней барабанной палочкой , или все возможные эхо-сигналы радара , которые можно получить от самолета , приближающегося к аэропорту .

В некоторых из этих ситуаций можно описать такое семейство волн функцией , которая зависит от определенных параметров , кроме и . Тогда можно получить разные волны – то есть разные функции и – выбирая разные значения для этих параметров. ${\displaystyle F(A,B,\ldots ;x,t)}$ ${\displaystyle A,B,\ldots }$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle x}$ ${\displaystyle t}$

Стоячая волна звукового давления в полуоткрытой трубе, воспроизводящая 7-ю гармонику основного тона ( n = 4)

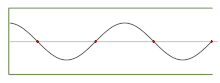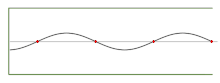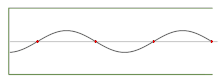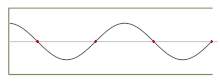
Например, звуковое давление внутри блокфлейты , воспроизводящей «чистую» ноту, обычно представляет собой стоячую волну , которую можно записать как

${\displaystyle F(A,L,n,c;x,t)=A\left(\cos 2\pi x{\frac {2n-1}{4L}}\right)\left(\cos 2\pi ct{\frac {2n-1}{4L}}\right)}$

Параметр определяет амплитуду волны (то есть максимальное звуковое давление в канале, которое связано с громкостью ноты); — скорость звука; — длина канала; и — положительное целое число (1,2,3,...), которое определяет количество узлов в стоячей волне. (Положение должно измеряться от мундштука , а время — от любого момента, в который давление в мундштуке максимально. Величина Не удалось проанализировать (синтаксическая ошибка): {\displaystyle \lambda = 4L/(2 n – 1)} — длина волны излучаемой ноты, а — ее частота .) Многие общие свойства этих волн можно вывести из этого общего уравнения, не выбирая конкретные значения для параметров. ${\displaystyle A}$ ${\displaystyle c}$ ${\displaystyle L}$ ${\displaystyle n}$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle f=c/\lambda }$

В качестве другого примера, может быть, что колебания кожи барабана после одного удара зависят только от расстояния от центра кожи до точки удара и от силы удара. Тогда колебания для всех возможных ударов можно описать функцией . ${\displaystyle r}$ ${\displaystyle s}$ ${\displaystyle F(r,s;x,t)}$

Иногда интересующее нас семейство волн имеет бесконечно много параметров. Например, можно описать, что происходит с температурой в металлическом стержне, когда его изначально нагревают до различных температур в разных точках по его длине, а затем дают ему остыть в вакууме. В этом случае вместо скаляра или вектора параметр должен быть функцией, такой что — начальная температура в каждой точке стержня. Тогда температуры в более поздние моменты времени можно выразить функцией , которая зависит от функции (то есть функциональным оператором ), так что температура в более поздние моменты времени равна ${\displaystyle h}$ ${\displaystyle h(x)}$ ${\displaystyle x}$ ${\displaystyle F}$ ${\displaystyle h}$ ${\displaystyle F(h;x,t)}$

Дифференциальные волновые уравнения

Другой способ описания и изучения семейства волн — дать математическое уравнение, которое вместо явного указания значения , ограничивает только то, как эти значения могут изменяться со временем. Тогда рассматриваемое семейство волн состоит из всех функций , которые удовлетворяют этим ограничениям, то есть всех решений уравнения. ${\displaystyle F(x,t)}$ ${\displaystyle F}$

Этот подход чрезвычайно важен в физике, поскольку ограничения обычно являются следствием физических процессов, которые заставляют волну эволюционировать. Например, если — температура внутри блока некоторого однородного и изотропного твердого материала, ее эволюция ограничена частным дифференциальным уравнением ${\displaystyle F(x,t)}$

${\displaystyle {\frac {\partial F}{\partial t}}(x,t)=\alpha \left({\frac {\partial ^{2}F}{\partial x_{1}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{2}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{3}^{2}}}(x,t)\right)+\beta Q(x,t)}$

где — тепло, которое выделяется в единицу объема и времени в окрестности в момент времени (например, за счет химических реакций, происходящих там); — декартовы координаты точки ; — (первая) производная по ; и — вторая производная по . (Символ « » означает, что в производной по некоторой переменной все остальные переменные должны считаться фиксированными.) ${\displaystyle Q(p,f)}$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle x_{1},x_{2},x_{3}}$ ${\displaystyle x}$ ${\displaystyle \partial F/\partial t}$ ${\displaystyle F}$ ${\displaystyle t}$ ${\displaystyle \partial ^{2}F/\partial x_{i}^{2}}$ ${\displaystyle F}$ ${\displaystyle x_{i}}$ ${\displaystyle \partial }$

Это уравнение можно вывести из законов физики, которые управляют диффузией тепла в твердых средах. По этой причине в математике его называют уравнением теплопроводности , хотя оно применимо ко многим другим физическим величинам, помимо температур.

В качестве другого примера, мы можем описать все возможные звуки, отражающиеся в контейнере с газом, функцией , которая дает давление в точке и времени внутри этого контейнера. Если газ изначально имел однородную температуру и состав, то эволюция ограничивается формулой ${\displaystyle F(x,t)}$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle F}$

${\displaystyle {\frac {\partial ^{2}F}{\partial t^{2}}}(x,t)=\alpha \left({\frac {\partial ^{2}F}{\partial x_{1}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{2}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{3}^{2}}}(x,t)\right)+\beta P(x,t)}$

Здесь имеется некоторая дополнительная сила сжатия, которая прикладывается к газу вблизи какого-то внешнего процесса, например, громкоговорителя или поршня, расположенного прямо рядом . ${\displaystyle P(x,t)}$ ${\displaystyle x}$ ${\displaystyle p}$

Это же дифференциальное уравнение описывает поведение механических колебаний и электромагнитных полей в однородном изотропном непроводящем твердом теле. Обратите внимание, что это уравнение отличается от уравнения теплового потока только тем, что левая часть — это , вторая производная по времени, а не первая производная . Однако это небольшое изменение имеет огромное значение для множества решений . Это дифференциальное уравнение в математике называется « волновым уравнением » , хотя оно описывает только один очень специальный вид волн. ${\displaystyle \partial ^{2}F/\partial t^{2}}$ ${\displaystyle F}$ ${\displaystyle \partial F/\partial t}$ ${\displaystyle F}$

Волна в упругой среде

Рассмотрим бегущую поперечную волну (которая может быть импульсом ) на струне (среде). Предположим, что струна имеет одно пространственное измерение. Рассмотрим эту волну как бегущую

Длину волны λ можно измерить между любыми двумя соответствующими точками на форме волны.

Анимация двух волн, зеленая волна движется вправо, а синяя волна движется влево, чистая амплитуда красной волны в каждой точке является суммой амплитуд отдельных волн. Обратите внимание, что f ( x , t ) + g ( x , t ) = u ( x , t ) .

• в направлении в пространстве. Например, пусть положительное направление будет направо, а отрицательное направление — налево. ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x}$
• с постоянной амплитудой ${\displaystyle u}$
• с постоянной скоростью , где ${\displaystyle v}$ ${\displaystyle v}$
  • не зависит от длины волны (нет дисперсии )
  • не зависит от амплитуды ( линейная среда, а не нелинейная ). ^{[4] [5]}
• с постоянной формой волны или формой

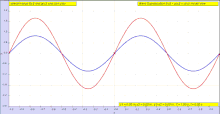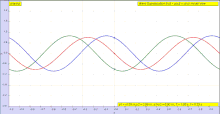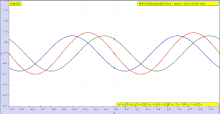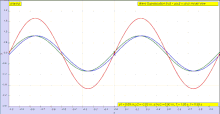
Эту волну можно описать двумерными функциями

• ${\displaystyle u(x,t)=F(x-vt)}$(волна движется вправо) ${\displaystyle F}$
• ${\displaystyle u(x,t)=G(x+vt)}$(волна движется влево) ${\displaystyle G}$

или, в более общем смысле, по формуле Даламбера : ^[6] представляющей две компонентные формы волн и распространяющиеся через среду в противоположных направлениях. Обобщенное представление этой волны может быть получено ^[7] как частное дифференциальное уравнение $${\displaystyle u(x,t)=F(x-vt)+G(x+vt).}$$ ${\displaystyle F}$ ${\displaystyle G}$ $${\displaystyle {\frac {1}{v^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}={\frac {\partial ^{2}u}{\partial x^{2}}}.}$$

Общие решения основаны на принципе Дюамеля . ^[8]

Формы волн

Синусоидальные , квадратные , треугольные и пилообразные формы волн

Форма или вид F в формуле Даламбера включает аргумент x − vt . Постоянные значения этого аргумента соответствуют постоянным значениям F , и эти постоянные значения возникают, если x увеличивается с той же скоростью, что и vt . То есть волна, имеющая форму функции F, будет двигаться в положительном направлении x со скоростью v (а G будет распространяться с той же скоростью в отрицательном направлении x ). ^[9]

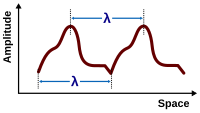
В случае периодической функции F с периодом λ , то есть F ( x + λ − vt ) = F ( x − vt ), периодичность F в пространстве означает, что снимок волны в заданное время t обнаруживает волну, периодически изменяющуюся в пространстве с периодом λ ( длина волны). Аналогичным образом, эта периодичность F подразумевает также периодичность во времени: F ( x − v ( t + T )) = F ( x − vt ) при условии vT = λ , поэтому наблюдение волны в фиксированном месте x обнаруживает волну, периодически колеблющуюся во времени с периодом T = λ / v . ^[10]

Амплитуда и модуляция

Амплитудная модуляция может быть достигнута с помощью f ( x , t ) = 1,00×sin(2π/0,10×( x −1,00× t )) и g ( x , t ) = 1,00×sin(2π/0,11×( x −1,00× t )) , только результирующая величина видна для улучшения ясности формы волны.

Иллюстрация огибающей ( медленно меняющаяся красная кривая) амплитудно-модулированной волны. Быстро меняющаяся синяя кривая — это несущая волна, которая модулируется.

Амплитуда волны может быть постоянной (в этом случае волна является непрерывной или непрерывной волной ) или может быть модулирована таким образом, чтобы изменяться со временем и/или положением. Очертание изменения амплитуды называется огибающей волны. Математически модулированную волну можно записать в виде: ^{[11] [12] [13]} где — огибающая амплитуды волны, — волновое число , а — фаза . Если групповая скорость (см. ниже) не зависит от длины волны, это уравнение можно упростить следующим образом: ^[14] показывая, что огибающая движется с групповой скоростью и сохраняет свою форму. В противном случае, в случаях, когда групповая скорость изменяется с длиной волны, форма импульса изменяется способом, часто описываемым с помощью уравнения огибающей . ^{[14] [15]} $${\displaystyle u(x,t)=A(x,t)\sin \left(kx-\omega t+\phi \right),}$$ ${\displaystyle A(x,\ t)}$ ${\displaystyle k}$ ${\displaystyle \phi }$ ${\displaystyle v_{g}}$ $${\displaystyle u(x,t)=A(x-v_{g}t)\sin \left(kx-\omega t+\phi \right),}$$

Фазовая скорость и групповая скорость

Красный квадрат движется с фазовой скоростью , а зеленые круги распространяются с групповой скоростью .

С волнами связаны две скорости: фазовая скорость и групповая скорость .

Фазовая скорость — это скорость, с которой фаза волны распространяется в пространстве : любая заданная фаза волны (например, гребень ) будет казаться движущейся с фазовой скоростью. Фазовая скорость задается в терминах длины волны λ (лямбда) и периода T как $${\displaystyle v_{\mathrm {p} }={\frac {\lambda }{T}}.}$$

Волна с групповой и фазовой скоростями, распространяющимися в разных направлениях

Групповая скорость — это свойство волн, имеющих определенную огибающую, измеряющее распространение в пространстве (то есть фазовую скорость) общей формы амплитуд волн — модуляции или огибающей волны.

Особые волны

Синусоидальные волны

Отслеживание компонента y окружности при движении по окружности приводит к синусоиде (красная). Отслеживание компонента x приводит к косинусоиде ( синяя ). Обе волны являются синусоидами одинаковой частоты, но разных фаз.

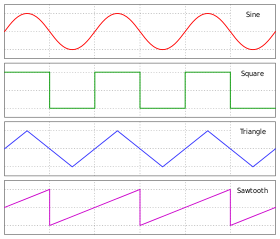
Синусоидальная волна , синусоидальная волна или синусоида (символ: ∿) — это периодическая волна, форма волны которой (форма) является тригонометрической синусоидальной функцией . В механике , как линейное движение во времени, это простое гармоническое движение ; как вращение , это соответствует равномерному круговому движению . Синусоидальные волны часто встречаются в физике , включая ветровые волны , звуковые волны и световые волны, такие как монохроматическое излучение . В технике , обработке сигналов и математике анализ Фурье разлагает общие функции на сумму синусоидальных волн различных частот, относительных фаз и величин.

Когда любые две синусоидальные волны одинаковой частоты (но произвольной фазы ) линейно объединяются , результатом является другая синусоидальная волна той же частоты; это свойство уникально среди периодических волн. И наоборот, если некоторая фаза выбрана в качестве нулевой отсчетной, синусоидальная волна произвольной фазы может быть записана как линейная комбинация двух синусоидальных волн с фазами ноль и четверть цикла, синусоидальной и косинусоидальной компонент , соответственно.

Плоские волны

Плоская волна — это вид волны, значение которой изменяется только в одном пространственном направлении. То есть ее значение постоянно на плоскости, перпендикулярной этому направлению. Плоские волны можно задать вектором единичной длины, указывающим направление, в котором изменяется волна, и профилем волны, описывающим, как волна изменяется в зависимости от смещения вдоль этого направления ( ) и времени ( ). Поскольку профиль волны зависит только от положения в комбинации , любое смещение в направлениях, перпендикулярных к , не может повлиять на значение поля. ${\displaystyle {\hat {n}}}$ ${\displaystyle {\hat {n}}\cdot {\vec {x}}}$ ${\displaystyle t}$ ${\displaystyle {\vec {x}}}$ ${\displaystyle {\hat {n}}\cdot {\vec {x}}}$ ${\displaystyle {\hat {n}}}$

Плоские волны часто используются для моделирования электромагнитных волн вдали от источника. Для электромагнитных плоских волн электрические и магнитные поля сами по себе являются поперечными к направлению распространения, а также перпендикулярными друг другу.

Стоячие волны

Стоячая волна. Красные точки представляют собой узлы волны .

Стоячая волна, также известная как стационарная волна , — это волна, огибающая которой остается в постоянном положении. Это явление возникает в результате интерференции двух волн, распространяющихся в противоположных направлениях.

Сумма двух встречных волн (равной амплитуды и частоты) создает стоячую волну . Стоячие волны обычно возникают, когда граница блокирует дальнейшее распространение волны, тем самым вызывая отражение волны и, следовательно, создавая встречную волну. Например, когда струна скрипки смещается, поперечные волны распространяются туда, где струна удерживается на месте у подставки и порожка , где волны отражаются обратно. У подставки и порожка две встречные волны находятся в противофазе и гасят друг друга, создавая узел . На полпути между двумя узлами находится пучность , где две встречные волны максимально усиливают друг друга. Нет чистого распространения энергии с течением времени.

• 
  Одномерные стоячие волны; основная мода и первые 5 обертонов
• 
  Двумерная стоячая волна на диске ; это основная мода.
• 
  Стоячая волна на диске с двумя узловыми линиями, пересекающимися в центре; это обертон.

Одиночные волны

Уединенная волна в лабораторном волновом канале

Солитон или уединенная волна — это самоусиливающийся волновой пакет , который сохраняет свою форму, распространяясь с постоянной скоростью. Солитоны возникают в результате аннулирования нелинейных и дисперсионных эффектов в среде. (Дисперсионные эффекты являются свойством определенных систем, в которых скорость волны зависит от ее частоты.) Солитоны — это решения широко распространенного класса слабонелинейных дисперсионных уравнений в частных производных, описывающих физические системы.

Физические свойства

Распространение

Распространение волн — это любой из способов, по которым распространяются волны. В зависимости от направления колебания относительно направления распространения различают продольные и поперечные волны .

Электромагнитные волны распространяются как в вакууме, так и в материальных средах. Распространение других типов волн, таких как звук, может происходить только в среде передачи .

Отражение плоских волн в полупространстве

Распространение и отражение плоских волн, например, волн давления ( волна P ) или волн сдвига (волны SH или SV), являются явлениями, которые впервые были охарактеризованы в области классической сейсмологии и теперь считаются фундаментальными концепциями в современной сейсмической томографии . Аналитическое решение этой проблемы существует и хорошо известно. Решение в частотной области может быть получено путем первого нахождения разложения Гельмгольца поля смещения, которое затем подставляется в волновое уравнение . Отсюда можно вычислить собственные моды плоской волны . ^{[ требуется цитата ] [ требуется пояснение ]}

Распространение волн SV

Распространение SV-волны в однородном полупространстве (горизонтальное поле смещений)

Распространение SV-волны в однородном полупространстве (Поле вертикального смещения) ^{[ требуется пояснение ]}

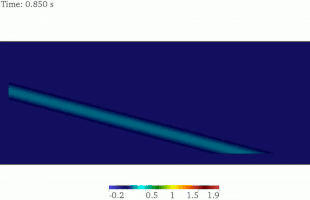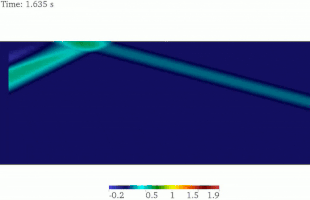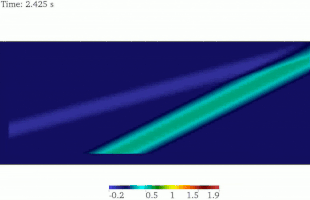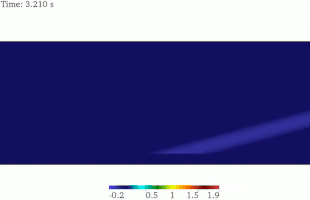
Аналитическое решение SV-волны в полупространстве показывает, что плоская SV-волна отражается обратно в область как P- и SV-волны, опуская особые случаи. Угол отраженной SV-волны идентичен падающей волне, в то время как угол отраженной P-волны больше, чем у SV-волны. Для той же частоты волны длина волны SV меньше, чем длина волны P. Этот факт был изображен на этой анимированной картинке. ^[16]

Распространение P-волны

Подобно волне SV, частота P, в общем, отражается как волна P и SV. Существуют некоторые особые случаи, когда режим отличается. ^{[ необходимо разъяснение ]}

Скорость волны

Распространение сейсмических волн в 2D-модели с использованием метода FDTD в присутствии мины

Скорость волны — это общее понятие, из различных видов скоростей волны, для фазы волны и скорости относительно распространения энергии (и информации). Фазовая скорость задается как: где: $${\displaystyle v_{\rm {p}}={\frac {\omega }{k}},}$$

• v _p — фазовая скорость (в системе СИ м/с),
• ω — угловая частота (единица СИ — рад/с),
• k — волновое число (единица измерения СИ — рад/м).

Фазовая скорость дает вам скорость, с которой точка постоянной фазы волны будет перемещаться для дискретной частоты. Угловая частота ω не может быть выбрана независимо от волнового числа k , но оба связаны дисперсионным соотношением : $${\displaystyle \omega =\Omega (k).}$$

В частном случае Ω( k ) = ck , где c — константа, волны называются недисперсионными, поскольку все частоты распространяются с одинаковой фазовой скоростью c . Например, электромагнитные волны в вакууме недисперсионны. В случае других форм дисперсионного соотношения мы имеем дисперсионные волны. Дисперсионное соотношение зависит от среды, через которую распространяются волны, и от типа волн (например, электромагнитные , звуковые или волны на воде ).

Скорость, с которой будет распространяться результирующий волновой пакет из узкого диапазона частот, называется групповой скоростью и определяется из градиента дисперсионного соотношения : $${\displaystyle v_{\rm {g}}={\frac {\partial \omega }{\partial k}}}$$

Почти во всех случаях волна — это в основном движение энергии через среду. Чаще всего групповая скорость — это скорость, с которой энергия движется через эту среду.

Световой луч демонстрирует отражение, преломление, пропускание и рассеивание при встрече с призмой

Волны демонстрируют общее поведение в ряде стандартных ситуаций, например:

Передача и средства массовой информации

Волны обычно движутся по прямой линии (то есть прямолинейно) через среду передачи . Такие среды можно классифицировать по одной или нескольким из следующих категорий:

• Ограниченная среда , если она имеет конечный размер, в противном случае — неограниченная среда.
• Линейная среда , если амплитуды различных волн в любой конкретной точке среды можно сложить.
• Однородная среда или гомогенная среда , если ее физические свойства неизменны в разных точках пространства.
• Анизотропная среда , если одно или несколько ее физических свойств различаются в одном или нескольких направлениях.
• Изотропная среда, если ее физические свойства одинаковы во всех направлениях.

Поглощение

Волны обычно определяются в средах, которые позволяют большей части или всей энергии волны распространяться без потерь . Однако материалы могут быть охарактеризованы как «потеряющие», если они забирают энергию из волны, обычно преобразуя ее в тепло. Это называется «поглощением». Материал, который поглощает энергию волны, либо при передаче, либо при отражении, характеризуется показателем преломления , который является комплексным . Величина поглощения, как правило, зависит от частоты (длины волны) волны, что, например, объясняет, почему объекты могут казаться цветными.

Отражение

Когда волна падает на отражающую поверхность, она меняет направление таким образом, что угол между падающей волной и линией , перпендикулярной поверхности, равен углу между отраженной волной и той же нормалью.

Рефракция

Синусоидальная бегущая плоская волна, входящая в область с меньшей скоростью волны под углом, иллюстрирующая уменьшение длины волны и изменение направления (рефракцию), что приводит к

Рефракция — это явление изменения скорости волны. Математически это означает, что изменяется величина фазовой скорости . Обычно рефракция происходит, когда волна переходит из одной среды в другую. Величина, на которую волна преломляется материалом, определяется показателем преломления материала. Направления падения и преломления связаны с показателями преломления двух материалов законом Снеллиуса .

Дифракция

Волна проявляет дифракцию, когда встречает препятствие, которое изгибает волну, или когда она распространяется после выхода из отверстия. Дифракционные эффекты более выражены, когда размер препятствия или отверстия сопоставим с длиной волны.

Вмешательство

Идентичные волны от двух источников, подвергающиеся интерференции . Внизу можно увидеть 5 положений, в которых волны складываются в фазе, но между которыми они находятся в противофазе и гасят друг друга.

Когда волны в линейной среде (обычный случай) пересекают друг друга в области пространства, они фактически не взаимодействуют друг с другом, а продолжают движение так, как будто другой волны нет. Однако в любой точке этой области величины поля, описывающие эти волны, складываются в соответствии с принципом суперпозиции . Если волны имеют одинаковую частоту в фиксированном фазовом соотношении, то, как правило, будут положения, в которых две волны находятся в фазе , а их амплитуды складываются , и другие положения, в которых они не совпадают по фазе , а их амплитуды (частично или полностью) компенсируются . Это называется интерференционной картиной .

Поляризация

Явление поляризации возникает, когда волновое движение может происходить одновременно в двух ортогональных направлениях. Поперечные волны могут быть поляризованы, например. Когда поляризация используется в качестве дескриптора без уточнения, это обычно относится к особому, простому случаю линейной поляризации . Поперечная волна линейно поляризована, если она колеблется только в одном направлении или плоскости. В случае линейной поляризации часто бывает полезно добавить относительную ориентацию той плоскости, перпендикулярной направлению движения, в которой происходит колебание, например, «горизонтальную», если плоскость поляризации параллельна земле. Электромагнитные волны, распространяющиеся в свободном пространстве, например, являются поперечными; они могут быть поляризованы с помощью поляризационного фильтра .

Продольные волны, такие как звуковые волны, не проявляют поляризации. Для этих волн существует только одно направление колебаний, а именно вдоль направления движения.

Дисперсия

Схема рассеивания света призмой. Нажмите, чтобы увидеть анимацию.

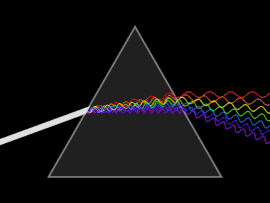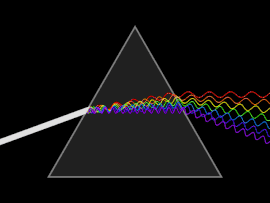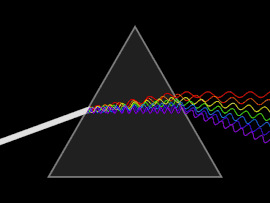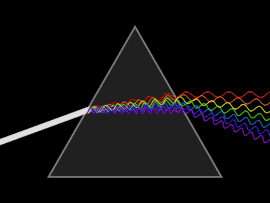
Волна подвергается дисперсии, когда либо фазовая скорость , либо групповая скорость зависят от частоты волны. Дисперсию легче всего наблюдать, пропуская белый свет через призму , результатом чего является создание спектра цветов радуги. Исаак Ньютон проводил эксперименты со светом и призмами, представляя свои выводы в Opticks (1704) о том, что белый свет состоит из нескольких цветов и что эти цвета не могут быть разложены дальше. ^[17]

эффект Доплера

Эффект Доплера или доплеровский сдвиг — это изменение частоты волны по отношению к наблюдателю, который движется относительно источника волны. ^[18] Он назван в честь австрийского физика Кристиана Доплера , который описал это явление в 1842 году.

Механические волны

Механическая волна представляет собой колебание материи и, следовательно, переносит энергию через среду . ^[19] В то время как волны могут перемещаться на большие расстояния, движение среды передачи — материала — ограничено. Поэтому колеблющийся материал не перемещается далеко от своего начального положения. Механические волны могут возникать только в средах, обладающих упругостью и инерцией . Существует три типа механических волн: поперечные волны , продольные волны и поверхностные волны .

Волны на струнах

Поперечная вибрация струны является функцией натяжения и инерции и ограничена длиной струны, поскольку концы закреплены. Это ограничение ограничивает возможные устойчивые режимы и, следовательно, частоты. Скорость поперечной волны, распространяющейся вдоль вибрирующей струны ( v ), прямо пропорциональна квадратному корню из натяжения струны ( T ) по линейной плотности массы ( μ ):

${\displaystyle v={\sqrt {\frac {T}{\mu }}},}$

где линейная плотность μ — масса на единицу длины струны.

Акустические волны

Акустические или звуковые волны — это волны сжатия, которые распространяются как объемные волны со скоростью, определяемой по формуле:

${\displaystyle v={\sqrt {\frac {B}{\rho _{0}}}},}$

или квадратный корень из адиабатического модуля упругости, деленный на плотность окружающей среды (см. скорость звука ).

Волны на воде

• Рябь на поверхности пруда на самом деле представляет собой комбинацию поперечных и продольных волн; поэтому точки на поверхности следуют по орбитальным траекториям.
• Звук  — механическая волна, распространяющаяся в газах, жидкостях, твёрдых телах и плазме;
• Инерционные волны , возникающие во вращающихся жидкостях и восстанавливаемые эффектом Кориолиса ;
• Волны на поверхности океана , представляющие собой возмущения, распространяющиеся в воде.

Объемные волны

Объемные волны распространяются внутри среды по траекториям, контролируемым свойствами материала с точки зрения плотности и модуля (жесткости). Плотность и модуль, в свою очередь, изменяются в зависимости от температуры, состава и фазы материала. Этот эффект напоминает преломление световых волн. Два типа движения частиц приводят к двум типам объемных волн: первичным и вторичным волнам.

Сейсмические волны

Сейсмические волны — это волны энергии, которые проходят через слои Земли и являются результатом землетрясений, извержений вулканов, движения магмы, крупных оползней и крупных искусственных взрывов, которые выдают низкочастотную акустическую энергию. Они включают объемные волны — первичные ( P-волны ) и вторичные волны ( S-волны ) — и поверхностные волны, такие как волны Рэлея , волны Лява и волны Стоунли .

Ударные волны

Формирование ударной волны самолетом

Ударная волна — это тип распространяющегося возмущения. Когда волна движется быстрее локальной скорости звука в жидкости , это ударная волна. Как и обычная волна, ударная волна переносит энергию и может распространяться через среду; однако она характеризуется резким, почти прерывистым изменением давления , температуры и плотности среды. ^[20]

Сдвиговые волны

Сдвиговые волны являются объемными волнами, обусловленными сдвиговой жесткостью и инерцией. Они могут передаваться только через твердые тела и в меньшей степени через жидкости с достаточно высокой вязкостью.

Другой

• Волны трафика , то есть распространение различных плотностей автотранспортных средств и т. д., которые можно моделировать как кинематические волны ^{[21] [22]}
• Метахрональная волна — это явление, характеризующееся появлением бегущей волны, возникающей в результате скоординированных последовательных действий.

Электромагнитные волны

Электромагнитная волна состоит из двух волн, которые являются колебаниями электрического и магнитного полей . Электромагнитная волна распространяется в направлении, которое находится под прямым углом к ​​направлению колебаний обоих полей. В 19 веке Джеймс Клерк Максвелл показал, что в вакууме электрическое и магнитное поля удовлетворяют волновому уравнению, оба со скоростью, равной скорости света . Из этого возникла идея, что свет является электромагнитной волной. Объединение света и электромагнитных волн было экспериментально подтверждено Герцем в конце 1880-х годов. Электромагнитные волны могут иметь разные частоты (и, следовательно, длины волн) и классифицируются соответственно по диапазонам волн, таким как радиоволны , микроволны , инфракрасное излучение , видимый свет , ультрафиолетовое излучение , рентгеновские лучи и гамма-лучи . Диапазон частот в каждом из этих диапазонов непрерывен, а пределы каждого диапазона в основном произвольны, за исключением видимого света, который должен быть виден нормальным человеческим глазом.

Квантово-механические волны

Уравнение Шредингера

Уравнение Шредингера описывает волнообразное поведение частиц в квантовой механике . Решения этого уравнения являются волновыми функциями , которые можно использовать для описания плотности вероятности частицы.

Уравнение Дирака

Уравнение Дирака — это релятивистское волновое уравнение, детализирующее электромагнитные взаимодействия. Волны Дирака полностью строго учитывали тонкие детали спектра водорода. Волновое уравнение также подразумевало существование новой формы материи, антиматерии, ранее не подозреваемой и не наблюдаемой, и которая была экспериментально подтверждена. В контексте квантовой теории поля уравнение Дирака интерпретируется заново для описания квантовых полей, соответствующих частицам со спином 1 ⁄ 2 .

Распространяющийся волновой пакет; в общем случае огибающая волнового пакета движется с другой скоростью, чем составляющие его волны. ^[23]

волны де Бройля

Луи де Бройль предположил, что все частицы с импульсом имеют длину волны

${\displaystyle \lambda ={\frac {h}{p}},}$

где h — постоянная Планка , а p — величина импульса частицы . Эта гипотеза легла в основу квантовой механики . В настоящее время эта длина волны называется длиной волны де Бройля . Например, электроны в дисплее ЭЛТ имеют длину волны де Бройля около 10−13 ^м  .

Волна, представляющая такую ​​частицу, движущуюся в направлении k , выражается волновой функцией следующим образом:

${\displaystyle \psi (\mathbf {r} ,\,t=0)=Ae^{i\mathbf {k\cdot r} },}$

где длина волны определяется волновым вектором k как:

${\displaystyle \lambda ={\frac {2\pi }{k}},}$

и импульс:

${\displaystyle \mathbf {p} =\hbar \mathbf {k} .}$

Однако такая волна с определенной длиной волны не локализована в пространстве и, следовательно, не может представлять частицу, локализованную в пространстве. Чтобы локализовать частицу, де Бройль предложил суперпозицию различных длин волн, расположенных вокруг центрального значения в волновом пакете ^[24] , форме волны, часто используемой в квантовой механике для описания волновой функции частицы. В волновом пакете длина волны частицы не является точной, а локальная длина волны отклоняется по обе стороны от основного значения длины волны.

При представлении волновой функции локализованной частицы волновой пакет часто принимается имеющим гауссову форму и называется гауссовым волновым пакетом . ^{[25] [26] [27]} Гауссовские волновые пакеты также используются для анализа волн на воде. ^[28]

Например, гауссова волновая функция ψ может иметь вид: ^[29]

${\displaystyle \psi (x,\,t=0)=A\exp \left(-{\frac {x^{2}}{2\sigma ^{2}}}+ik_{0}x\right),}$

в некоторый начальный момент времени t = 0, где центральная длина волны связана с центральным волновым вектором k ₀ как λ ₀ = 2π / k ₀ . Хорошо известно из теории анализа Фурье [ ^30] или из принципа неопределенности Гейзенберга (в случае квантовой механики), что для создания локализованного волнового пакета необходим узкий диапазон длин волн, и чем более локализована огибающая, тем больше разброс требуемых длин волн. Преобразование Фурье гауссианы само является гауссовой функцией. ^[31] Учитывая гауссиану:

${\displaystyle f(x)=e^{-x^{2}/\left(2\sigma ^{2}\right)},}$

преобразование Фурье имеет вид:

${\displaystyle {\tilde {f}}(k)=\sigma e^{-\sigma ^{2}k^{2}/2}.}$

Таким образом, гауссово распределение в пространстве состоит из волн:

${\displaystyle f(x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\ {\tilde {f}}(k)e^{ikx}\ dk;}$

то есть число волн с длиной волны λ, такое, что kλ = 2 π.

Параметр σ определяет пространственное распространение гауссианы вдоль оси x , в то время как преобразование Фурье показывает распространение волнового вектора k, определяемое как 1/ σ . То есть, чем меньше протяженность в пространстве, тем больше протяженность в k , и, следовательно, в λ = 2π/ k .

Анимация, демонстрирующая воздействие кросс-поляризованной гравитационной волны на кольцо тестовых частиц.

Гравитационные волны

Гравитационные волны — это волны, которые генерируются в жидкой среде или на границе двух сред, когда сила тяжести или плавучести работает на восстановление равновесия. Поверхностные волны на воде — наиболее известный пример.

Гравитационные волны

Гравитационные волны также распространяются в пространстве. Первое наблюдение гравитационных волн было объявлено 11 февраля 2016 года. ^[32] Гравитационные волны — это возмущения кривизны пространства-времени , предсказанные общей теорией относительности Эйнштейна .

Смотрите также

• Индекс статей волны

Волны в целом

• Механическая волна , в среде передачи
• Волновое уравнение , общее
• Интерференция волн — явление, при котором две волны накладываются друг на друга, образуя результирующую волну.
• Wave Motion (журнал) , научный журнал
• Волновой фронт , продвигающаяся поверхность распространения волны.

Параметры

• Частота
• Фаза (волны) , смещение или угол синусоидальной волновой функции в ее начале
• Коэффициент стоячей волны в телекоммуникациях
• Длина волны
• Волновое число

Формы волн

• Ползучая волна , волна, дифрагированная вокруг сферы.
• Эфемерное поле
• Продольная волна
• Периодическая бегущая волна
• Синусоидальная волна
• Прямоугольная волна
• Стоячая волна
• Поперечная волна

Электромагнитные волны

• Поверхностная волна Дьяконова
• Волна Дьяконова–Фойгта
• Волновод Земля-ионосфера , в радиопередаче
• Электромагнитное излучение
• Уравнение электромагнитной волны описывает распространение электромагнитной волны.
• Микроволны , форма электромагнитного излучения

В жидкостях

• Теория волн Эйри в динамике жидкости
• Капиллярная волна в динамике жидкости
• Кноидальная волна в динамике жидкости
• Краевая волна , поверхностная гравитационная волна, зафиксированная путем преломления на жесткой границе.
• Волна Фарадея , тип волны в жидкостях.
• Гравитационная волна в гидродинамике
• Внутренняя волна , волна внутри жидкой среды.
• Ударная волна в аэродинамике
• Звуковая волна, волна звука, проходящая через среду, например воздух или воду.
• Приливная волна — научно неверное название цунами
• Волна Толлмина – Шлихтинга в гидродинамике
• Ветровая волна

В квантовой механике

• Теорема Блоха
• Волна материи
• Теория пилотной волны в механике Бома
• Волновая функция
• Волновой пакет
• Корпускулярно-волновой дуализм

В теории относительности

• Гравитационная волна в теории относительности
• Релятивистские волновые уравнения , волновые уравнения, которые учитывают специальную теорию относительности
• pp-волновое пространство-время , набор точных решений уравнения поля Эйнштейна

Другие специфические типы волн

• Альвеновская волна в физике плазмы.
• Атмосферная волна , периодическое возмущение полей атмосферных переменных.
• Еловая волна , конфигурация леса
• Волны Лэмба в твердых материалах
• Волна Рэлея , поверхностные акустические волны, распространяющиеся по твердым телам.
• Спиновая волна в магнетизме
• Волна спиновой плотности в твердых материалах
• Троянский волновой пакет в науке о частицах
• Волны в плазме , в физике плазмы

Похожие темы

• Поглощение (электромагнитное излучение)
• Антенна (радио)
• Бит (акустика)
• Разветвленный поток
• Киматика
• Дифракция
• Дисперсия (волны на воде)
• эффект Доплера
• Детектор конвертов
• Преобразование Фурье для вычисления периодичности в равномерно распределенных данных
• Групповая скорость
• Гармонический
• Принцип Гюйгенса-Френеля
• Индекс статей волны
• Инерционная волна
• Спектральный анализ методом наименьших квадратов для вычисления периодичности в неравномерно распределенных данных
• Список волн, названных в честь людей
• Фазовая скорость
• Фотон
• Поляризация (физика)
• Постоянная распространения
• Распространение радиоволн
• Луч (оптика)
• Система реакция-диффузия
• Отражение (физика)
• Рефракция
• Резонанс
• Танк с волнами
• Волна-убийца
• Рассеивание
• Уравнения мелкой воды
• Машина для создания волн Shive
• Звук
• Стоячая волна
• Среда передачи
• Фактор скорости
• Волновое уравнение
• Энергия волн
• Волновая турбулентность
• Ветровая волна
• Ветровая волна#Формирование

Ссылки

1. (Холл 1980, стр. 8)
2. Прагнан Чакраворти, «Что такое сигнал? [Конспект лекций]», Журнал обработки сигналов IEEE , т. 35, № 5, стр. 175–177, сентябрь 2018 г.  doi : 10.1109/MSP.2018.2832195
3. Сантос, Эдгар; Шёлль, Михаэль; Санчес-Поррас, Ренан; Далем, Маркус А.; Силос, Умберто; Унтерберг, Андреас; Дикхаус, Хартмут; Саковиц, Оливер В. (2014-10-01). «Радиальные, спиральные и реверберирующие волны распространяющейся деполяризации возникают в гиренцефалическом мозге». NeuroImage . 99 : 244–255. doi :10.1016/j.neuroimage.2014.05.021. ISSN  1095-9572. PMID  24852458. S2CID  1347927.
4. Майкл А. Славински (2003). "Волновые уравнения". Сейсмические волны и лучи в упругих средах . Elsevier. стр. 131 и далее . ISBN 978-0-08-043930-3.
5. Лев А. Островский и Александр И. Потапов (2001). Модулированные волны: теория и применение. Johns Hopkins University Press. ISBN 978-0-8018-7325-6.
6. Грааф, Карл Ф. (1991). Волновое движение в упругих твердых телах (Переиздание Оксфордского издания 1975 г.). Довер. С. 13–14. ISBN 978-0-486-66745-4.
7. Для примера вывода см. шаги, ведущие к уравнению (17) в Redfern, Francis. "Kinematic Derivation of the Wave Equation". Physics Journal . Архивировано из оригинала 2013-07-24 . Получено 2012-12-11 .
8. Джалал М. Ихсан Шатах; Майкл Струве (2000). "Линейное волновое уравнение". Геометрические волновые уравнения . Книжный магазин Американского математического общества. стр. 37 и далее . ISBN 978-0-8218-2749-9.
9. Луис Лайонс (1998). Все, что вы хотели знать о математике, но боялись спросить. Cambridge University Press. С. 128 и далее . ISBN 978-0-521-43601-4.
10. Макферсон, Александр (2009). «Волны и их свойства». Введение в макромолекулярную кристаллографию (2-е изд.). Wiley. стр. 77. ISBN 978-0-470-18590-2.
11. Кристиан Йираушек (2005). Динамика лазера FEW-цикла и обнаружение фазы огибающей несущей. Cuvillier Verlag. стр. 9. ISBN 978-3-86537-419-6.
12. Фриц Курт Кнойбюль (1997). Колебания и волны. Springer. стр. 365. ISBN 978-3-540-62001-3.
13. Марк Лундстром (2000). Основы транспорта носителей. Cambridge University Press. стр. 33. ISBN 978-0-521-63134-1.
14. Chin-Lin Chen (2006). "§13.7.3 Огибающая импульса в недисперсионных средах". Основы волноводной оптики . Wiley. стр. 363. ISBN 978-0-471-75687-3.
15. Лонги, Стефано; Джаннер, Давиде (2008). «Локализация и волновые пакеты Ванье в фотонных кристаллах». В Hugo E. Hernández-Figueroa; Michel Zamboni-Rached; Erasmo Recami (ред.). Локализованные волны . Wiley-Interscience. стр. 329. ISBN 978-0-470-10885-7.
16. Анимации взяты из Poursartip, Babak (2015). "Топографическое усиление сейсмических волн". UT Austin. Архивировано из оригинала 2017-01-09 . Получено 2023-02-24 .
17. Ньютон, Исаак (1704). "Prop VII Theor V". Opticks: Or, A treatise of the Reflections, Refractions, Inflexions and Colours of Light. Also Two treatises of the Species and Magnitude of Curvilinear Figures . Vol. 1. London. p. 118. Все цвета во Вселенной, которые созданы Светом... являются либо цветами однородных Светов, либо составлены из них...
18. Джордано, Николас (2009). Колледжская физика: рассуждения и отношения. Cengage Learning. стр. 421–424. ISBN 978-0534424718.
19. Джанколи, Д.К. (2009) Физика для ученых и инженеров с современной физикой (4-е изд.). Аппер Сэдл Ривер, Нью-Джерси: Pearson Prentice Hall.
20. Андерсон, Джон Д. младший (январь 2001 г.) [1984], Основы аэродинамики (3-е изд.), McGraw-Hill Science/Engineering/Math , ISBN 978-0-07-237335-6
21. MJ Lighthill ; GB Whitham (1955). «О кинематических волнах. II. Теория транспортного потока на длинных загруженных дорогах». Труды Лондонского королевского общества. Серия A . 229 (1178): 281–345. Bibcode :1955RSPSA.229..281L. CiteSeerX 10.1.1.205.4573 . doi :10.1098/rspa.1955.0088. S2CID  18301080. 
22. PI Richards (1956). «Ударные волны на шоссе». Исследование операций . 4 (1): 42–51. doi :10.1287/opre.4.1.42.
23. AT Fromhold (1991). "Решения волнового пакета". Квантовая механика для прикладной физики и инженерии (переиздание Academic Press 1981 ed.). Courier Dover Publications. стр. 59 и далее . ISBN 978-0-486-66741-6. (стр. 61) ...отдельные волны движутся медленнее, чем пакет, и поэтому проходят обратно через пакет по мере его продвижения
24. Мин Чианг Ли (1980). "Интерференция электронов". В L. Marton; Клэр Мартон (ред.). Достижения в электронике и электронной физике . Т. 53. Academic Press. стр. 271. ISBN 978-0-12-014653-6.
25. Уолтер Грейнер; Д. Аллан Бромли (2007). Квантовая механика (2-е изд.). Springer. стр. 60. ISBN 978-3-540-67458-0.
26. Джон Джозеф Гилман (2003). Электронные основы прочности материалов. Cambridge University Press. стр. 57. ISBN 978-0-521-62005-5.
27. Дональд Д. Фиттс (1999). Принципы квантовой механики. Cambridge University Press. стр. 17. ISBN 978-0-521-65841-6.
28. Чианг С. Мэй (1989). Прикладная динамика поверхностных волн океана (2-е изд.). World Scientific. стр. 47. ISBN 978-9971-5-0789-3.
29. Грейнер, Уолтер; Бромли, Д. Аллан (2007). Квантовая механика (2-е изд.). Springer. стр. 60. ISBN 978-3-540-67458-0.
30. Зигмунд Брандт; Ганс Дитер Дамен (2001). Книжка с картинками по квантовой механике (3-е изд.). Спрингер. п. 23. ISBN 978-0-387-95141-6.
31. Сайрус Д. Кантрелл (2000). Современные математические методы для физиков и инженеров . Cambridge University Press. стр. 677. ISBN 978-0-521-59827-9.
32. «Гравитационные волны обнаружены впервые, «открывают совершенно новое окно во вселенную». Канадская вещательная корпорация. 11 февраля 2016 г.

Источники

• Флейш, Д.; Киннаман, Л. (2015). Путеводитель по волнам для школьников . Кембридж: Издательство Кембриджского университета. Бибкод : 2015sgw..книга.....F. ISBN 978-1107643260.
• Кэмпбелл, Мюррей; Грейтед, Клайв (2001). Руководство музыканта по акустике (переиздание). Оксфорд: Oxford University Press. ISBN 978-0198165057.
• Френч, AP (1971). Вибрации и волны (серия Вводная физика MIT) . Нельсон Торнс. ISBN 978-0-393-09936-2. OCLC  163810889.
• Холл, Д.Э. (1980). Музыкальная акустика: Введение . Белмонт, Калифорния: Wadsworth Publishing Company. ISBN 978-0-534-00758-4..
• Хант, Фредерик Винтон (1978). Истоки акустики . Вудбери, Нью-Йорк: Опубликовано для Акустического общества Америки через Американский институт физики. ISBN 978-0300022209.
• Островский, LA; Потапов, AS (1999). Модулированные волны, теория и приложения . Балтимор: Издательство Университета Джонса Хопкинса. ISBN 978-0-8018-5870-3..
• Гриффитс, Г.; Шиссер, У. Э. (2010). Анализ бегущих волн уравнений с частными производными: численные и аналитические методы с Matlab и Maple . Academic Press. ISBN 9780123846532.
• Crawford jr., Frank S. (1968). Волны (курс физики в Беркли, том 3) , McGraw-Hill, ISBN 978-0070048607 Бесплатная онлайн-версия 
• AEH Love (1944). Трактат о математической теории упругости . Нью-Йорк: Довер .
• EW Weisstein. "Скорость волны". ScienceWorld . Получено 2009-05-30 .

Внешние ссылки

• Фейнмановские лекции по физике: волны
• Линейные и нелинейные волны
• Science Aid: Свойства волн – Краткое руководство для подростков
• «Архивы AT&T: сходства поведения волн», продемонстрированные Дж. Н. Шайвом из Bell Labs (видео на YouTube )