Определитель

In mathematics, invariant of square matrices

В математике определитель — это скалярная функция элементов квадратной матрицы . Определитель матрицы A обычно обозначается det( A ) , det A или | A | . Его значение характеризует некоторые свойства матрицы и линейного отображения , представленного на заданном базисе матрицей. В частности, определитель не равен нулю тогда и только тогда, когда матрица обратима и соответствующее линейное отображение является изоморфизмом .

Определитель полностью определяется двумя следующими свойствами: определитель произведения матриц равен произведению их определителей, а определитель треугольной матрицы равен произведению ее диагональных элементов.

Определитель матрицы 2 × 2 равен

${\displaystyle {\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc,}$

а определитель матрицы 3 × 3 равен

${\displaystyle {\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=aei+bfg+cdh-ceg-bdi-afh.}$

Определитель матрицы n × n можно определить несколькими эквивалентными способами, наиболее распространенным из которых является формула Лейбница , которая выражает определитель как сумму ( факториала n ) знаковых произведений элементов матрицы. Его можно вычислить с помощью разложения Лапласа , которое выражает определитель как линейную комбинацию определителей подматриц, или с помощью исключения Гаусса , что позволяет вычислить ступенчатую форму строки с тем же определителем , равным произведению диагональных элементов ступенчатой ​​формы строки. ${\displaystyle n!}$

Определители также могут быть определены некоторыми их свойствами. А именно, определитель — это уникальная функция, определенная на матрицах n × n , которая имеет четыре следующих свойства:

1. Определитель единичной матрицы равен 1 .
2. Перестановка двух строк умножает определитель на −1 .
3. Умножение строки на число умножает определитель на это число.
4. Добавление кратного одной строки к другой строке не меняет определитель.

Приведенные выше свойства, относящиеся к строкам (свойства 2–4), можно заменить соответствующими утверждениями относительно столбцов.

Определитель инвариантен относительно подобия матриц . Это означает, что при заданном линейном эндоморфизме конечномерного векторного пространства определитель матрицы, представляющей его на базисе, не зависит от выбранного базиса. Это позволяет определить определитель линейного эндоморфизма, который не зависит от выбора системы координат .

Определители встречаются во всей математике. Например, матрица часто используется для представления коэффициентов в системе линейных уравнений , и определители могут использоваться для решения этих уравнений ( правило Крамера ), хотя другие методы решения вычислительно гораздо более эффективны. Определители используются для определения характеристического многочлена квадратной матрицы, корни которой являются собственными значениями . В геометрии знаковый n -мерный объем n -мерного параллелепипеда выражается определителем, а определитель линейного эндоморфизма определяет, как ориентация и n -мерный объем преобразуются при эндоморфизме. Это используется в исчислении с внешними дифференциальными формами и определителем Якоби , в частности, для замены переменных в кратных интегралах .

Матрицы два на два

Определитель матрицы 2 × 2 обозначается либо « det », либо вертикальными чертами вокруг матрицы и определяется как ${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$

${\displaystyle \det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.}$

Например,

${\displaystyle \det {\begin{pmatrix}3&7\\1&-4\end{pmatrix}}={\begin{vmatrix}3&7\\1&{-4}\end{vmatrix}}=(3\cdot (-4))-(7\cdot 1)=-19.}$

Первые свойства

Определитель имеет несколько ключевых свойств, которые можно доказать путем прямой оценки определения для -матриц, и которые продолжают выполняться для определителей больших матриц. Они следующие: ^[1] во-первых, определитель единичной матрицы равен 1. Во-вторых, определитель равен нулю, если две строки одинаковы: ${\displaystyle 2\times 2}$ ${\displaystyle {\begin{pmatrix}1&0\\0&1\end{pmatrix}}}$

${\displaystyle {\begin{vmatrix}a&b\\a&b\end{vmatrix}}=ab-ba=0.}$

Это справедливо и в том случае, если два столбца одинаковы. Более того,

${\displaystyle {\begin{vmatrix}a&b+b'\\c&d+d'\end{vmatrix}}=a(d+d')-(b+b')c={\begin{vmatrix}a&b\\c&d\end{vmatrix}}+{\begin{vmatrix}a&b'\\c&d'\end{vmatrix}}.}$

Наконец, если какой-либо столбец умножается на некоторое число (т. е. все записи в этом столбце умножаются на это число), определитель также умножается на это число: ${\displaystyle r}$

${\displaystyle {\begin{vmatrix}r\cdot a&b\\r\cdot c&d\end{vmatrix}}=rad-brc=r(ad-bc)=r\cdot {\begin{vmatrix}a&b\\c&d\end{vmatrix}}.}$

Геометрическое значение

Площадь параллелограмма — это абсолютное значение определителя матрицы, образованной векторами, представляющими стороны параллелограмма.

Если элементы матрицы являются действительными числами, матрица A может быть использована для представления двух линейных отображений : одно, которое отображает стандартные базисные векторы в строки A , и другое, которое отображает их в столбцы A. В любом случае образы базисных векторов образуют параллелограмм , который представляет собой образ единичного квадрата при отображении. Параллелограмм, определяемый строками указанной выше матрицы, имеет вершины в (0, 0) , ( a , b ) , ( a + c , b + d ) и ( c , d ) , как показано на прилагаемой диаграмме.

Абсолютное значение ad − bc является площадью параллелограмма и, таким образом, представляет собой масштабный коэффициент, с помощью которого площади преобразуются с помощью A. (Параллелограмм, образованный столбцами A, в общем случае является другим параллелограммом, но поскольку определитель симметричен относительно строк и столбцов, площадь будет той же.)

Абсолютное значение определителя вместе со знаком становится знаковой площадью параллелограмма. Знаковая площадь такая же, как и обычная площадь , за исключением того, что она отрицательна, когда угол между первым и вторым векторами, определяющими параллелограмм, поворачивается по часовой стрелке (что противоположно направлению, которое можно было бы получить для единичной матрицы ).

Чтобы показать, что ad − bc является знаковой площадью, можно рассмотреть матрицу, содержащую два вектора u ≡ ( a , b ) и v ≡ ( c , d ), представляющих стороны параллелограмма. Знаковая площадь может быть выражена как | u | | v | sin θ для угла θ между векторами, который является просто основанием, умноженным на высоту, длиной одного вектора, умноженной на перпендикулярную составляющую другого. Из-за синуса это уже знаковая площадь, однако ее можно выразить более удобно, используя косинус дополнительного угла к перпендикулярному вектору, например u ^⊥ = (− b , a ) , так что | u ^⊥ | | v | cos θ′ становится рассматриваемой знаковой площадью, которая может быть определена по шаблону скалярного произведения как равная ad − bc согласно следующим уравнениям:

${\displaystyle {\text{Signed area}}=|{\boldsymbol {u}}|\,|{\boldsymbol {v}}|\,\sin \,\theta =\left|{\boldsymbol {u}}^{\perp }\right|\,\left|{\boldsymbol {v}}\right|\,\cos \,\theta '={\begin{pmatrix}-b\\a\end{pmatrix}}\cdot {\begin{pmatrix}c\\d\end{pmatrix}}=ad-bc.}$

Объем этого параллелепипеда равен абсолютному значению определителя матрицы, образованной столбцами, построенными из векторов r1, r2 и r3.

Таким образом, определитель дает масштабный коэффициент и ориентацию, индуцированную отображением, представленным A. Когда определитель равен единице, линейное отображение, определяемое матрицей, является равноплощадным и сохраняющим ориентацию.

Объект, известный как бивектор, связан с этими идеями. В 2D его можно интерпретировать как ориентированный плоский сегмент , образованный представлением двух векторов, каждый из которых имеет начало (0, 0) и координаты ( a , b ) и ( c , d ) . Величина бивектора (обозначаемая как ( a , b ) ∧ ( c , d ) ) — это площадь со знаком , которая также является определителем ad − bc . ^[2]

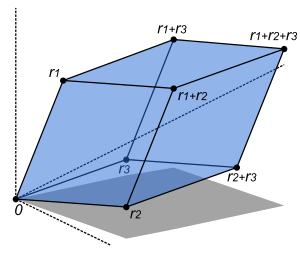
Если действительная матрица A размером n × n записана в терминах ее векторов-столбцов , то ${\displaystyle A=\left[{\begin{array}{c|c|c|c}\mathbf {a} _{1}&\mathbf {a} _{2}&\cdots &\mathbf {a} _{n}\end{array}}\right]}$

${\displaystyle A{\begin{pmatrix}1\\0\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{1},\quad A{\begin{pmatrix}0\\1\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{2},\quad \ldots ,\quad A{\begin{pmatrix}0\\0\\\vdots \\1\end{pmatrix}}=\mathbf {a} _{n}.}$

Это означает, что отображает единичный n -мерный куб в n -мерный параллелоэдр, определяемый векторами области ${\displaystyle A}$ ${\displaystyle \mathbf {a} _{1},\mathbf {a} _{2},\ldots ,\mathbf {a} _{n},}$ ${\displaystyle P=\left\{c_{1}\mathbf {a} _{1}+\cdots +c_{n}\mathbf {a} _{n}\mid 0\leq c_{i}\leq 1\ \forall i\right\}.}$

Определитель дает знаковый n -мерный объем этого параллелоэдра и, следовательно, описывает в более общем виде n -мерный коэффициент масштабирования объема линейного преобразования, произведенного A . ^[3] (Знак показывает, сохраняет ли преобразование или меняет ориентацию .) В частности, если определитель равен нулю, то этот параллелоэдр имеет нулевой объем и не является полностью n -мерным, что указывает на то, что размерность образа A меньше n . Это означает , что A производит линейное преобразование, которое не является ни на , ни взаимно-однозначным , и поэтому не является обратимым. ${\displaystyle \det(A)=\pm {\text{vol}}(P),}$

Определение

Пусть A — квадратная матрица с n строками и n столбцами, так что ее можно записать как

${\displaystyle A={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{bmatrix}}.}$

Записи и т. д., для многих целей, являются действительными или комплексными числами. Как обсуждается ниже, определитель также определяется для матриц, записи которых находятся в коммутативном кольце . ${\displaystyle a_{1,1}}$

Определитель матрицы A обозначается как det( A ) или его можно обозначить непосредственно через элементы матрицы, написав окружающие черты вместо скобок:

${\displaystyle {\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{vmatrix}}.}$

Существуют различные эквивалентные способы определения определителя квадратной матрицы A , т. е. матрицы с тем же числом строк и столбцов: определитель можно определить с помощью формулы Лейбница , явной формулы, включающей суммы произведений определенных элементов матрицы. Определитель также можно охарактеризовать как уникальную функцию, зависящую от элементов матрицы, удовлетворяющих определенным свойствам. Этот подход также можно использовать для вычисления определителей путем упрощения рассматриваемых матриц.

формула Лейбница

Матрицы 3 × 3

Формула Лейбница для определителя матрицы 3 × 3 выглядит следующим образом:

${\displaystyle {\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=aei+bfg+cdh-ceg-bdi-afh.\ }$

В этом выражении каждый член имеет один множитель из каждой строки, все в разных столбцах, расположенных в порядке возрастания строк. Например, bdi имеет b из первой строки второго столбца, d из второй строки первого столбца и i из третьей строки третьего столбца. Знаки определяются тем, сколько транспозиций множителей необходимо для расположения множителей в порядке возрастания их столбцов (учитывая, что члены расположены слева направо в порядке возрастания строк): положительный для четного числа транспозиций и отрицательный для нечетного числа. Для примера bdi одиночная транспозиция bd в db дает dbi, три множителя которого находятся из первого, второго и третьего столбцов соответственно; это нечетное число транспозиций, поэтому член появляется со знаком минус.

Правило Сарруса

Правило Сарруса является мнемоническим для расширенной формы этого определителя: сумма произведений трех диагональных линий элементов матрицы с северо-запада на юго-восток, минус сумма произведений трех диагональных линий элементов матрицы с юго-запада на северо-восток, когда копии первых двух столбцов матрицы записаны рядом с ней, как на иллюстрации. Эта схема вычисления определителя матрицы 3 × 3 не переносится в более высокие измерения.

н×нматрицы

Обобщая вышесказанное на более высокие измерения, определитель матрицы — это выражение, включающее перестановки и их сигнатуры . Перестановка множества — это биективная функция из этого множества в себя, со значениями, исчерпывающими весь набор. Множество всех таких перестановок, называемое симметрической группой , обычно обозначается как . Сигнатура перестановки — это если перестановку можно получить с четным числом транспозиций (обменов двух записей); в противном случае она ${\displaystyle n\times n}$ ${\displaystyle \{1,2,\dots ,n\}}$ ${\displaystyle \sigma }$ ${\displaystyle \sigma (1),\sigma (2),\ldots ,\sigma (n)}$ ${\displaystyle S_{n}}$ ${\displaystyle \operatorname {sgn}(\sigma )}$ ${\displaystyle \sigma }$ ${\displaystyle +1,}$ ${\displaystyle -1.}$

Дана матрица

${\displaystyle A={\begin{bmatrix}a_{1,1}\ldots a_{1,n}\\\vdots \qquad \vdots \\a_{n,1}\ldots a_{n,n}\end{bmatrix}},}$

формула Лейбница для ее определителя, используя сигма-обозначение для суммы, имеет вид

${\displaystyle \det(A)={\begin{vmatrix}a_{1,1}\ldots a_{1,n}\\\vdots \qquad \vdots \\a_{n,1}\ldots a_{n,n}\end{vmatrix}}=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )a_{1,\sigma (1)}\cdots a_{n,\sigma (n)}.}$

Используя обозначение Пи для произведения, это можно сократить до

${\displaystyle \det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma (i)}\right)}$.

Символ Леви-Чивиты определяется на n - кортежах целых чисел в как 0 , если два из целых чисел равны, и в противном случае как сигнатура перестановки, определяемой n- кортежом целых чисел. С символом Леви-Чивиты формула Лейбница становится ${\displaystyle \varepsilon _{i_{1},\ldots ,i_{n}}}$ ${\displaystyle \{1,\ldots ,n\}}$

${\displaystyle \det(A)=\sum _{i_{1},i_{2},\ldots ,i_{n}}\varepsilon _{i_{1}\cdots i_{n}}a_{1,i_{1}}\!\cdots a_{n,i_{n}},}$

где сумма берется по всем n -кортежам целых чисел из ^{[4] [5]} ${\displaystyle \{1,\ldots ,n\}.}$

Свойства определителя

Характеристика определителя

Определитель можно охарактеризовать следующими тремя ключевыми свойствами. Чтобы сформулировать их, удобно рассматривать -матрицу A как состоящую из ее столбцов, поэтому обозначаемую как ${\displaystyle n\times n}$ ${\displaystyle n}$

${\displaystyle A={\big (}a_{1},\dots ,a_{n}{\big )},}$

где вектор-столбец (для каждого i ) состоит из элементов матрицы в i -м столбце. ${\displaystyle a_{i}}$

2. ${\displaystyle \det \left(I\right)=1}$, где — единичная матрица . ${\displaystyle I}$
4. Определитель является полилинейным : если j -й столбец матрицы записан в виде линейной комбинации двух векторов-столбцов v и w и числа r , то определитель A можно выразить в виде аналогичной линейной комбинации: ${\displaystyle A}$ ${\displaystyle a_{j}=r\cdot v+w}$

   ${\displaystyle {\begin{aligned}|A|&={\big |}a_{1},\dots ,a_{j-1},r\cdot v+w,a_{j+1},\dots ,a_{n}|\\&=r\cdot |a_{1},\dots ,v,\dots a_{n}|+|a_{1},\dots ,w,\dots ,a_{n}|\end{aligned}}}$

6. Определитель является знакопеременным : если два столбца матрицы идентичны, то ее определитель равен 0:

   ${\displaystyle |a_{1},\dots ,v,\dots ,v,\dots ,a_{n}|=0.}$

Если определитель определен с использованием формулы Лейбница, как указано выше, эти три свойства могут быть доказаны путем прямого изучения этой формулы. Некоторые авторы также подходят к определителю напрямую, используя эти три свойства: можно показать, что существует ровно одна функция, которая присваивает любой -матрице A число, удовлетворяющее этим трем свойствам. ^[6] Это также показывает, что этот более абстрактный подход к определителю дает то же определение, что и подход с использованием формулы Лейбница. ${\displaystyle n\times n}$

Чтобы увидеть это, достаточно разложить определитель по мультилинейности в столбцах в (огромную) линейную комбинацию определителей матриц, в которой каждый столбец является стандартным базисным вектором. Эти определители либо равны 0 (по свойству 9), либо ±1 (по свойствам 1 и 12 ниже), поэтому линейная комбинация дает приведенное выше выражение в терминах символа Леви-Чивиты. Хотя эта характеристика выглядит менее технической, она не может полностью заменить формулу Лейбница при определении определителя, поскольку без нее существование соответствующей функции неясно. ^{[ необходима цитата ]}

Немедленные последствия

Эти правила имеют ряд дополнительных последствий:

• Определитель является однородной функцией , т.е. (для матрицы ). $${\displaystyle \det(cA)=c^{n}\det(A)}$$ ${\displaystyle n\times n}$ ${\displaystyle A}$
• Перестановка любой пары столбцов матрицы умножает ее определитель на −1. Это следует из того, что определитель является полилинейным и знакопеременным (свойства 2 и 3 выше): Эту формулу можно применять итеративно, когда меняются местами несколько столбцов. Например : Еще более общо, любая перестановка столбцов умножает определитель на знак перестановки. $${\displaystyle |a_{1},\dots ,a_{j},\dots a_{i},\dots ,a_{n}|=-|a_{1},\dots ,a_{i},\dots ,a_{j},\dots ,a_{n}|.}$$ $${\displaystyle |a_{3},a_{1},a_{2},a_{4}\dots ,a_{n}|=-|a_{1},a_{3},a_{2},a_{4},\dots ,a_{n}|=|a_{1},a_{2},a_{3},a_{4},\dots ,a_{n}|.}$$
• Если какой-то столбец можно выразить как линейную комбинацию других столбцов (т. е. столбцы матрицы образуют линейно зависимый набор), то определитель равен 0. В качестве особого случая сюда входит: если какой-то столбец таков, что все его элементы равны нулю, то определитель этой матрицы равен 0.
• Добавление скалярного кратного одного столбца к другому столбцу не изменяет значение определителя. Это следствие полилинейности и альтернативности: в силу полилинейности определитель изменяется на кратное определителя матрицы с двумя равными столбцами, определитель которой равен 0, поскольку определитель является знакопеременным.
• Если — треугольная матрица , т. е . , всякий раз, когда или, альтернативно, всякий раз , когда , то ее определитель равен произведению диагональных элементов: Действительно, такую ​​матрицу можно сократить, соответствующим образом добавив кратные столбцы с меньшим количеством ненулевых элементов к столбцам с большим количеством элементов, до диагональной матрицы (без изменения определителя). Для такой матрицы использование линейности в каждом столбце сводится к единичной матрице, и в этом случае указанная формула выполняется по самому первому характеристическому свойству определителей. Альтернативно, эту формулу можно также вывести из формулы Лейбница, поскольку единственная перестановка, которая дает ненулевой вклад, — это единичная перестановка. ${\displaystyle A}$ ${\displaystyle a_{ij}=0}$ ${\displaystyle i>j}$ ${\displaystyle i<j}$ $${\displaystyle \det(A)=a_{11}a_{22}\cdots a_{nn}=\prod _{i=1}^{n}a_{ii}.}$$ ${\displaystyle \sigma }$

Пример

Эти характерные свойства и их следствия, перечисленные выше, являются теоретически значимыми, но также могут быть использованы для вычисления определителей для конкретных матриц. Фактически, исключение Гаусса может быть применено для приведения любой матрицы к верхней треугольной форме, и шаги в этом алгоритме влияют на определитель контролируемым образом. Следующий конкретный пример иллюстрирует вычисление определителя матрицы с использованием этого метода: ${\displaystyle A}$

${\displaystyle A={\begin{bmatrix}-2&-1&2\\2&1&4\\-3&3&-1\end{bmatrix}}.}$

Объединение этих равенств дает ${\displaystyle |A|=-|E|=-(18\cdot 3\cdot (-1))=54.}$

Транспонировать

Определитель транспонированного числа равен определителю числа A : ${\displaystyle A}$

${\displaystyle \det \left(A^{\textsf {T}}\right)=\det(A)}$.

Это можно доказать, проверив формулу Лейбница. ^[7] Это подразумевает, что во всех свойствах, упомянутых выше, слово «столбец» может быть заменено на «строка» повсюду. Например, рассматривая матрицу n × n как состоящую из n строк, определитель является n -линейной функцией.

Мультипликативность и матричные группы

Определитель является мультипликативным отображением , т.е. для квадратных матриц одинакового размера определитель произведения матриц равен произведению их определителей: ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle \det(AB)=\det(A)\det(B)}$

Этот ключевой факт можно доказать, наблюдая, что для фиксированной матрицы обе стороны уравнения являются чередующимися и полилинейными как функция, зависящая от столбцов . Более того, они обе принимают значение, когда — единичная матрица. Вышеупомянутая уникальная характеристика чередующихся полилинейных отображений, таким образом, показывает это утверждение. ^[8] ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle \det B}$ ${\displaystyle A}$

Матрица с элементами в поле обратима точно , если ее определитель ненулевой. Это следует из мультипликативности определителя и формулы для обратной матрицы, включающей присоединенную матрицу, упомянутую ниже. В этом случае определитель обратной матрицы задается как ${\displaystyle A}$

${\displaystyle \det \left(A^{-1}\right)={\frac {1}{\det(A)}}=[\det(A)]^{-1}}$.

В частности, произведения и обратные матрицы с ненулевым определителем (соответственно, определитель один) все еще обладают этим свойством. Таким образом, множество таких матриц (фиксированного размера над полем ) образует группу, известную как общая линейная группа (соответственно, подгруппа, называемая специальной линейной группой . В более общем смысле, слово «специальная» указывает на подгруппу другой матричной группы матриц с определителем один. Примерами являются специальная ортогональная группа (которая, если n равно 2 или 3, состоит из всех матриц вращения ) и специальная унитарная группа . ${\displaystyle n}$ ${\displaystyle K}$ ${\displaystyle \operatorname {GL} _{n}(K)}$ ${\displaystyle \operatorname {SL} _{n}(K)\subset \operatorname {GL} _{n}(K)}$

Поскольку определитель уважает умножение и обратные, он фактически является групповым гомоморфизмом из в мультипликативную группу ненулевых элементов . Этот гомоморфизм сюръективен, а его ядром является (матрицы с определителем единица). Следовательно, по первой теореме об изоморфизме это показывает, что является нормальной подгруппой , и что фактор-группа изоморфна . ${\displaystyle \operatorname {GL} _{n}(K)}$ ${\displaystyle K^{\times }}$ ${\displaystyle K}$ ${\displaystyle \operatorname {SL} _{n}(K)}$ ${\displaystyle \operatorname {SL} _{n}(K)}$ ${\displaystyle \operatorname {GL} _{n}(K)}$ ${\displaystyle \operatorname {GL} _{n}(K)/\operatorname {SL} _{n}(K)}$ ${\displaystyle K^{\times }}$

Формула Коши–Бине является обобщением этой формулы произведения для прямоугольных матриц. Эту формулу можно также переформулировать как мультипликативную формулу для составных матриц, элементы которой являются определителями всех квадратичных подматриц данной матрицы. ^{[9] [10]}

расширение Лапласа

Разложение Лапласа выражает определитель матрицы рекурсивно через определители меньших матриц, известных как ее миноры . Минор определяется как определитель -матрицы , которая получается путем удаления -й строки и -го столбца. Выражение известно как сомножитель . Для каждого имеет место равенство ${\displaystyle A}$ ${\displaystyle M_{i,j}}$ ${\displaystyle (n-1)\times (n-1)}$ ${\displaystyle A}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle (-1)^{i+j}M_{i,j}}$ ${\displaystyle i}$

${\displaystyle \det(A)=\sum _{j=1}^{n}(-1)^{i+j}a_{i,j}M_{i,j},}$

что называется разложением Лапласа по i -й строке . Например, разложение Лапласа по первой строке ( ) дает следующую формулу: ${\displaystyle i=1}$

${\displaystyle {\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=a{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c{\begin{vmatrix}d&e\\g&h\end{vmatrix}}}$

Развертывание определителей этих -матриц возвращает формулу Лейбница, упомянутую выше. Аналогично, разложение Лапласа по -му столбцу есть равенство ${\displaystyle 2\times 2}$ ${\displaystyle j}$

${\displaystyle \det(A)=\sum _{i=1}^{n}(-1)^{i+j}a_{i,j}M_{i,j}.}$

Разложение Лапласа можно использовать итеративно для вычисления определителей, но этот подход неэффективен для больших матриц. Однако он полезен для вычисления определителей высокосимметричных матриц, таких как матрица Вандермонда . Разложение Лапласа по n - члену вдоль строки или столбца можно обобщить , чтобы записать определитель n x n как сумму членов , каждый из которых является произведением определителя подматрицы k x k и определителя дополнительной подматрицы ( n−k ) x ( n−k ). $${\displaystyle {\begin{vmatrix}1&1&1&\cdots &1\\x_{1}&x_{2}&x_{3}&\cdots &x_{n}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}&\cdots &x_{n}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{1}^{n-1}&x_{2}^{n-1}&x_{3}^{n-1}&\cdots &x_{n}^{n-1}\end{vmatrix}}=\prod _{1\leq i<j\leq n}\left(x_{j}-x_{i}\right).}$$ ${\displaystyle {\tbinom {n}{k}}}$

Сопрягаемая матрица

Сопряжённая матрица является транспонированной матрицей кофакторов, то есть, ${\displaystyle \operatorname {adj} (A)}$

${\displaystyle (\operatorname {adj} (A))_{i,j}=(-1)^{i+j}M_{ji}.}$

Для каждой матрицы имеется ^[11]

${\displaystyle (\det A)I=A\operatorname {adj} A=(\operatorname {adj} A)\,A.}$

Таким образом, присоединенную матрицу можно использовать для выражения обратной невырожденной матрицы :

${\displaystyle A^{-1}={\frac {1}{\det A}}\operatorname {adj} A.}$

Блочные матрицы

Формула для определителя -матрицы выше продолжает выполняться, при соответствующих дальнейших предположениях, для блочной матрицы , т.е. матрицы, состоящей из четырех подматриц размерности , , и , соответственно. Самая простая такая формула, которая может быть доказана с использованием либо формулы Лейбница, либо факторизации с использованием дополнения Шура , это ${\displaystyle 2\times 2}$ ${\displaystyle A,B,C,D}$ ${\displaystyle m\times m}$ ${\displaystyle m\times n}$ ${\displaystyle n\times m}$ ${\displaystyle n\times n}$

${\displaystyle \det {\begin{pmatrix}A&0\\C&D\end{pmatrix}}=\det(A)\det(D)=\det {\begin{pmatrix}A&B\\0&D\end{pmatrix}}.}$

Если обратим , то из результатов раздела о мультипликативности следует, что ${\displaystyle A}$

${\displaystyle {\begin{aligned}\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}&=\det(A)\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}\underbrace {\det {\begin{pmatrix}A^{-1}&-A^{-1}B\\0&I_{n}\end{pmatrix}}} _{=\,\det(A^{-1})\,=\,(\det A)^{-1}}\\&=\det(A)\det {\begin{pmatrix}I_{m}&0\\CA^{-1}&D-CA^{-1}B\end{pmatrix}}\\&=\det(A)\det(D-CA^{-1}B),\end{aligned}}}$

что упрощается до случая, когда является -матрицей. ${\displaystyle \det(A)(D-CA^{-1}B)}$ ${\displaystyle D}$ ${\displaystyle 1\times 1}$

Аналогичный результат имеет место, когда обратим, а именно ${\displaystyle D}$

${\displaystyle {\begin{aligned}\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}&=\det(D)\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}\underbrace {\det {\begin{pmatrix}I_{m}&0\\-D^{-1}C&D^{-1}\end{pmatrix}}} _{=\,\det(D^{-1})\,=\,(\det D)^{-1}}\\&=\det(D)\det {\begin{pmatrix}A-BD^{-1}C&BD^{-1}\\0&I_{n}\end{pmatrix}}\\&=\det(D)\det(A-BD^{-1}C).\end{aligned}}}$

Оба результата можно объединить для вывода теоремы Сильвестра об определителях , которая также изложена ниже.

Если блоки являются квадратными матрицами одинакового размера , то дальнейшие формулы справедливы. Например, если и коммутируют (т.е. ), то ^[12] ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle CD=DC}$

${\displaystyle \det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(AD-BC).}$

Эта формула была обобщена на матрицы, состоящие из более чем блоков, снова при соответствующих условиях коммутативности между отдельными блоками. ^[13] ${\displaystyle 2\times 2}$

Для и справедлива следующая формула (даже если и не коммутируют) ^{[ необходима ссылка ]} ${\displaystyle A=D}$ ${\displaystyle B=C}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle \det {\begin{pmatrix}A&B\\B&A\end{pmatrix}}=\det(A-B)\det(A+B).}$

Теорема Сильвестра об определителе

Теорема Сильвестра об определителях гласит, что для A , матрицы размером m × n , и B , матрицы размером n × m (так что A и B имеют размеры, позволяющие умножать их в любом порядке, образуя квадратную матрицу):

${\displaystyle \det \left(I_{\mathit {m}}+AB\right)=\det \left(I_{\mathit {n}}+BA\right),}$

где I _m и I _n — единичные матрицы размером m × m и n × n соответственно.

Из этого общего результата вытекает несколько следствий.

1. Для случая вектора-столбца c и вектора-строки r , каждый из которых имеет m компонентов, формула позволяет быстро вычислить определитель матрицы, которая отличается от единичной матрицы на матрицу ранга 1:

   ${\displaystyle \det \left(I_{\mathit {m}}+cr\right)=1+rc.}$

2. В более общем смысле, ^[14] для любой обратимой матрицы X размером m × m ,
   ${\displaystyle \det(X+AB)=\det(X)\det \left(I_{\mathit {n}}+BX^{-1}A\right),}$
3. Для вектора столбца и строки, как указано выше:
   ${\displaystyle \det(X+cr)=\det(X)\det \left(1+rX^{-1}c\right)=\det(X)+r\,\operatorname {adj} (X)\,c.}$
4. Для квадратных матриц и одинакового размера матрицы и имеют одинаковые характеристические многочлены (следовательно, одинаковые собственные значения). ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle AB}$ ${\displaystyle BA}$

Сумма

Определитель суммы двух квадратных матриц одинакового размера в общем случае не выражается через определители матриц A и B. ${\displaystyle A+B}$

Однако для положительно полуопределенных матриц и одинакового размера, с учетом следствия [ ^{15] [16]} ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ $${\displaystyle \det(A+B+C)+\det(C)\geq \det(A+C)+\det(B+C){\text{,}}}$$ $${\displaystyle \det(A+B)\geq \det(A)+\det(B){\text{.}}}$$

Из теоремы Брунна–Минковского следует, что корень n- й степени определителя является вогнутой функцией при ограничении эрмитовыми положительно-определенными матрицами. ^[17] Следовательно, если A и B являются эрмитовыми положительно-определенными матрицами, то имеем, поскольку корень n- й степени определителя является однородной функцией . ${\displaystyle n\times n}$ ${\displaystyle n\times n}$ $${\displaystyle {\sqrt[{n}]{\det(A+B)}}\geq {\sqrt[{n}]{\det(A)}}+{\sqrt[{n}]{\det(B)}},}$$

Сумма тождеств для матриц 2×2

Для частного случая матриц с комплексными элементами определитель суммы можно записать через определители и следы в следующем тождестве: ${\displaystyle 2\times 2}$

${\displaystyle \det(A+B)=\det(A)+\det(B)+{\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).}$

Подтверждение личности

Это можно показать, расписав каждый член по компонентам . Левая часть — ${\displaystyle A_{ij},B_{ij}}$

${\displaystyle (A_{11}+B_{11})(A_{22}+B_{22})-(A_{12}+B_{12})(A_{21}+B_{21}).}$

Расширение дает

${\displaystyle A_{11}A_{22}+B_{11}A_{22}+A_{11}B_{22}+B_{11}B_{22}-A_{12}A_{21}-B_{12}A_{21}-A_{12}B_{21}-B_{12}B_{21}.}$

Видно, что члены, квадратичные по , равны , и аналогично для , поэтому выражение можно записать ${\displaystyle A}$ ${\displaystyle \det(A)}$ ${\displaystyle B}$

${\displaystyle \det(A)+\det(B)+A_{11}B_{22}+B_{11}A_{22}-A_{12}B_{21}-B_{12}A_{21}.}$

Затем мы можем записать перекрестные члены как

${\displaystyle (A_{11}+A_{22})(B_{11}+B_{22})-(A_{11}B_{11}+A_{12}B_{21}+A_{21}B_{12}+A_{22}B_{22})}$

который может быть признан как

${\displaystyle {\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).}$

что завершает доказательство.

Это имеет приложение к матричным алгебрам. Например, рассмотрим комплексные числа как матричную алгебру. Комплексные числа имеют представление в виде матриц вида с и вещественными. Так как , то взятие и в приведенном выше тождестве дает ${\displaystyle 2\times 2}$ $${\displaystyle aI+b\mathbf {i} :=a{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+b{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}}$$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle {\text{tr}}(\mathbf {i} )=0}$ ${\displaystyle A=aI}$ ${\displaystyle B=b\mathbf {i} }$

${\displaystyle \det(aI+b\mathbf {i} )=a^{2}\det(I)+b^{2}\det(\mathbf {i} )=a^{2}+b^{2}.}$

Этот результат вытекает как раз из и . ${\displaystyle {\text{tr}}(\mathbf {i} )=0}$ ${\displaystyle \det(I)=\det(\mathbf {i} )=1}$

Свойства определителя по отношению к другим понятиям

Собственные значения и характеристический полином

Определитель тесно связан с двумя другими центральными понятиями в линейной алгебре, собственными значениями и характеристическим многочленом матрицы. Пусть будет -матрицей с комплексными элементами. Тогда, по Основной теореме алгебры, должно иметь ровно n собственных значений . (Здесь подразумевается, что собственное значение с алгебраической кратностью μ встречается μ раз в этом списке.) Тогда оказывается, что определитель A равен произведению этих собственных значений, ${\displaystyle A}$ ${\displaystyle n\times n}$ ${\displaystyle A}$ ${\displaystyle \lambda _{1},\lambda _{2},\ldots ,\lambda _{n}}$

${\displaystyle \det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.}$

Произведение всех ненулевых собственных значений называется псевдодетерминантом .

Из этого сразу видно, что определитель матрицы равен нулю тогда и только тогда, когда является собственным значением . Другими словами, обратим тогда и только тогда, когда не является собственным значением . ${\displaystyle A}$ ${\displaystyle 0}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle 0}$ ${\displaystyle A}$

Характеристический многочлен определяется как ^[18]

${\displaystyle \chi _{A}(t)=\det(t\cdot I-A).}$

Здесь — неопределенность многочлена, а — единичная матрица того же размера, что и . С помощью этого многочлена можно использовать определители для нахождения собственных значений матрицы : они являются в точности корнями этого многочлена, т. е. теми комплексными числами, что ${\displaystyle t}$ ${\displaystyle I}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle \lambda }$

${\displaystyle \chi _{A}(\lambda )=0.}$

Эрмитова матрица положительно определена , если все ее собственные значения положительны. Критерий Сильвестра утверждает, что это эквивалентно определителям подматриц

${\displaystyle A_{k}:={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,k}\\a_{2,1}&a_{2,2}&\cdots &a_{2,k}\\\vdots &\vdots &\ddots &\vdots \\a_{k,1}&a_{k,2}&\cdots &a_{k,k}\end{bmatrix}}}$

будучи положительным, для всех между и . ^[19] ${\displaystyle k}$ ${\displaystyle 1}$ ${\displaystyle n}$

След

След tr( A ) по определению является суммой диагональных элементов A и также равен сумме собственных значений. Таким образом, для комплексных матриц A ,

${\displaystyle \det(\exp(A))=\exp(\operatorname {tr} (A))}$

или, для действительных матриц A ,

${\displaystyle \operatorname {tr} (A)=\log(\det(\exp(A))).}$

Здесь exp( A ) обозначает матричную экспоненту A , поскольку каждое собственное значение λ матрицы A соответствует собственному значению exp( λ ) матрицы exp( A ). В частности, если задан любой логарифм A , то есть любая матрица L , удовлетворяющая

${\displaystyle \exp(L)=A}$

определитель A определяется как

${\displaystyle \det(A)=\exp(\operatorname {tr} (L)).}$

Например, для n = 2 , n = 3 и n = 4 соответственно,

${\displaystyle {\begin{aligned}\det(A)&={\frac {1}{2}}\left(\left(\operatorname {tr} (A)\right)^{2}-\operatorname {tr} \left(A^{2}\right)\right),\\\det(A)&={\frac {1}{6}}\left(\left(\operatorname {tr} (A)\right)^{3}-3\operatorname {tr} (A)~\operatorname {tr} \left(A^{2}\right)+2\operatorname {tr} \left(A^{3}\right)\right),\\\det(A)&={\frac {1}{24}}\left(\left(\operatorname {tr} (A)\right)^{4}-6\operatorname {tr} \left(A^{2}\right)\left(\operatorname {tr} (A)\right)^{2}+3\left(\operatorname {tr} \left(A^{2}\right)\right)^{2}+8\operatorname {tr} \left(A^{3}\right)~\operatorname {tr} (A)-6\operatorname {tr} \left(A^{4}\right)\right).\end{aligned}}}$

cf. Теорема Кэли-Гамильтона . Такие выражения выводятся из комбинаторных аргументов, тождеств Ньютона или алгоритма Фаддеева-Леверье . То есть, для общего n , det A = (−1) ⁿ c ₀ знаковый постоянный член характеристического многочлена , определяемый рекурсивно из

${\displaystyle c_{n}=1;~~~c_{n-m}=-{\frac {1}{m}}\sum _{k=1}^{m}c_{n-m+k}\operatorname {tr} \left(A^{k}\right)~~(1\leq m\leq n)~.}$

В общем случае это также можно получить из ^[20]

${\displaystyle \det(A)=\sum _{\begin{array}{c}k_{1},k_{2},\ldots ,k_{n}\geq 0\\k_{1}+2k_{2}+\cdots +nk_{n}=n\end{array}}\prod _{l=1}^{n}{\frac {(-1)^{k_{l}+1}}{l^{k_{l}}k_{l}!}}\operatorname {tr} \left(A^{l}\right)^{k_{l}},}$

где сумма берется по множеству всех целых чисел k _l ≥ 0, удовлетворяющих уравнению

${\displaystyle \sum _{l=1}^{n}lk_{l}=n.}$

Формулу можно выразить через полный экспоненциальный полином Белла от n аргументов s _l = −( l – 1)! tr( A ^l ) как

${\displaystyle \det(A)={\frac {(-1)^{n}}{n!}}B_{n}(s_{1},s_{2},\ldots ,s_{n}).}$

Эту формулу можно также использовать для нахождения определителя матрицы A ^I _J с многомерными индексами I = ( i ₁ , i ₂ , ..., i _r ) и J = ( j ₁ , j ₂ , ..., j _r ) . Произведение и след таких матриц определяются естественным образом как

${\displaystyle (AB)_{J}^{I}=\sum _{K}A_{K}^{I}B_{J}^{K},\operatorname {tr} (A)=\sum _{I}A_{I}^{I}.}$

Важное произвольное тождество размерности n может быть получено из разложения логарифма в ряд Меркатора , когда разложение сходится. Если каждое собственное значение A меньше 1 по абсолютной величине,

${\displaystyle \det(I+A)=\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,}$

где I — единичная матрица. В более общем случае, если

${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}s^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,}$

разлагается в формальный степенной ряд по s, то все коэффициенты s ^m при m > n равны нулю, а оставшийся многочлен равен det( I + sA ) .

Верхние и нижние границы

Для положительно определенной матрицы A оператор трассировки дает следующие точные нижние и верхние границы определителя логарифма:

${\displaystyle \operatorname {tr} \left(I-A^{-1}\right)\leq \log \det(A)\leq \operatorname {tr} (A-I)}$

с равенством тогда и только тогда, когда A = I. Это соотношение можно вывести с помощью формулы для расхождения Кульбака-Лейблера между двумя многомерными нормальными распределениями.

Также,

${\displaystyle {\frac {n}{\operatorname {tr} \left(A^{-1}\right)}}\leq \det(A)^{\frac {1}{n}}\leq {\frac {1}{n}}\operatorname {tr} (A)\leq {\sqrt {{\frac {1}{n}}\operatorname {tr} \left(A^{2}\right)}}.}$

Эти неравенства можно доказать, выразив следы и определитель через собственные значения. Таким образом, они представляют собой хорошо известный факт, что среднее гармоническое меньше среднего геометрического , которое меньше среднего арифметического , которое, в свою очередь, меньше среднего квадратичного .

Производный

Формула Лейбница показывает, что определитель действительных (или аналогично для комплексных) квадратных матриц является полиномиальной функцией от до . В частности, она всюду дифференцируема . Ее производная может быть выражена с помощью формулы Якоби : ^[21] ${\displaystyle \mathbf {R} ^{n\times n}}$ ${\displaystyle \mathbf {R} }$

${\displaystyle {\frac {d\det(A)}{d\alpha }}=\operatorname {tr} \left(\operatorname {adj} (A){\frac {dA}{d\alpha }}\right).}$

где обозначает сопряжение . В частности, если обратимо, то имеем ${\displaystyle \operatorname {adj} (A)}$ ${\displaystyle A}$ ${\displaystyle A}$

${\displaystyle {\frac {d\det(A)}{d\alpha }}=\det(A)\operatorname {tr} \left(A^{-1}{\frac {dA}{d\alpha }}\right).}$

Выраженные в терминах записей , они являются ${\displaystyle A}$

${\displaystyle {\frac {\partial \det(A)}{\partial A_{ij}}}=\operatorname {adj} (A)_{ji}=\det(A)\left(A^{-1}\right)_{ji}.}$

Еще одна эквивалентная формулировка:

${\displaystyle \det(A+\epsilon X)-\det(A)=\operatorname {tr} (\operatorname {adj} (A)X)\epsilon +O\left(\epsilon ^{2}\right)=\det(A)\operatorname {tr} \left(A^{-1}X\right)\epsilon +O\left(\epsilon ^{2}\right)}$,

с использованием большой нотации O. Особый случай, когда , единичная матрица, дает ${\displaystyle A=I}$

${\displaystyle \det(I+\epsilon X)=1+\operatorname {tr} (X)\epsilon +O\left(\epsilon ^{2}\right).}$

Это тождество используется при описании алгебр Ли, связанных с определенными матричными группами Ли . Например, специальная линейная группа определяется уравнением . Приведенная выше формула показывает, что ее алгебра Ли является специальной линейной алгеброй Ли, состоящей из тех матриц, след которых равен нулю. ${\displaystyle \operatorname {SL} _{n}}$ ${\displaystyle \det A=1}$ ${\displaystyle {\mathfrak {sl}}_{n}}$

Записав -матрицу как , где - векторы-столбцы длины 3, тогда градиент по одному из трех векторов можно записать как векторное произведение двух других: ${\displaystyle 3\times 3}$ ${\displaystyle A={\begin{bmatrix}a&b&c\end{bmatrix}}}$ ${\displaystyle a,b,c}$

${\displaystyle {\begin{aligned}\nabla _{\mathbf {a} }\det(A)&=\mathbf {b} \times \mathbf {c} \\\nabla _{\mathbf {b} }\det(A)&=\mathbf {c} \times \mathbf {a} \\\nabla _{\mathbf {c} }\det(A)&=\mathbf {a} \times \mathbf {b} .\end{aligned}}}$

История

Исторически определители использовались задолго до матриц: Определитель изначально определялся как свойство системы линейных уравнений . Определитель «определяет», имеет ли система единственное решение (что происходит именно тогда, когда определитель не равен нулю). В этом смысле определители впервые были использованы в китайском учебнике математики «Девять глав математического искусства» (九章算術, китайские ученые, около 3-го века до н. э.). В Европе решения линейных систем из двух уравнений были выражены Кардано в 1545 году с помощью сущности, похожей на определитель. ^[22]

Собственно определители возникли отдельно из работы Секи Такакадзу в 1683 году в Японии и параллельно Лейбница в 1693 году. ^{[23] [24] [25] [26]} Крамер (1750) сформулировал правило Крамера без доказательства. ^[27] И Крамер, и Безу (1779) пришли к определителям из вопроса о плоских кривых, проходящих через заданный набор точек. ^[28]

Вандермонд (1771) первым признал определители как независимые функции. ^[24] Лаплас (1772) дал общий метод разложения определителя по его дополнительным минорам : Вандермонд уже привел частный случай. ^[29] Сразу же после этого Лагранж (1773) рассмотрел определители второго и третьего порядка и применил их к вопросам теории исключения ; он доказал много частных случаев общих тождеств.

Гаусс (1801) сделал следующий шаг. Подобно Лагранжу, он широко использовал детерминанты в теории чисел . Он ввел слово «детерминант» (Лаплас использовал слово «результант»), хотя и не в настоящем значении, а скорее в применении к дискриминанту квантической функции . ^[30] Гаусс также пришел к понятию обратных (обратных) детерминантов и очень близко подошел к теореме умножения. ^{[ необходимо разъяснение ]}

Следующим по значимости был Бине (1811, 1812), который формально сформулировал теорему, касающуюся произведения двух матриц из m столбцов и n строк, которая для частного случая m = n сводится к теореме умножения. В тот же день (30 ноября 1812 г.), когда Бине представил свою работу в Академии, Коши также представил свою работу по этой теме. (См. формулу Коши–Бине .) В ней он использовал слово «детерминант» в его нынешнем смысле, ^{[31] [32]} обобщил и упростил то, что тогда было известно по этой теме, улучшил обозначения и дал теорему умножения с доказательством, более удовлетворительным, чем у Бине. ^{[24] [33]} С него начинается теория в ее общности.

Якоби (1841) использовал функциональный определитель, который Сильвестр позже назвал якобианом . [ ^34] В своих мемуарах в журнале Крелля за 1841 год он специально рассматривает эту тему, а также класс знакопеременных функций, которые Сильвестр назвал альтернантами . Примерно во время последних мемуаров Якоби Сильвестр (1839) и Кейли начали свою работу. Кейли в 1841 году ввел современную нотацию для определителя с использованием вертикальных черт. ^{[35] [36]}

Изучение специальных форм определителей стало естественным результатом завершения общей теории. Осесимметричные определители изучались Лебегом , Гессе и Сильвестром; персимметричные определители — Сильвестром и Ганкелем ; циркулянты — Каталаном , Споттисвудом , Глейшером и Скоттом; косые определители и пфаффианы в связи с теорией ортогональных преобразований — Кэли; континуанты — Сильвестром; вронскианы (так называемые Мюиром ) — Кристоффелем и Фробениусом ; составные определители — Сильвестром, Рейссом и Пике; якобианы и гессианы — Сильвестром; и симметричные гош-определители — Труди . Из учебников по этому предмету учебник Споттисвуда был первым. В Америке трактаты опубликовали Ганус (1886), Уэлд (1893) и Мьюир/Мецлер (1933).

Приложения

Правило Крамера

Определители могут быть использованы для описания решений линейной системы уравнений , записанной в матричной форме как . Это уравнение имеет единственное решение тогда и только тогда, когда не равно нулю. В этом случае решение дается правилом Крамера : ${\displaystyle Ax=b}$ ${\displaystyle x}$ ${\displaystyle \det(A)}$

${\displaystyle x_{i}={\frac {\det(A_{i})}{\det(A)}}\qquad i=1,2,3,\ldots ,n}$

где - матрица, образованная заменой -го столбца на вектор-столбец . Это следует непосредственно из столбцового разложения определителя, т.е. ${\displaystyle A_{i}}$ ${\displaystyle i}$ ${\displaystyle A}$ ${\displaystyle b}$

${\displaystyle \det(A_{i})=\det {\begin{bmatrix}a_{1}&\ldots &b&\ldots &a_{n}\end{bmatrix}}=\sum _{j=1}^{n}x_{j}\det {\begin{bmatrix}a_{1}&\ldots &a_{i-1}&a_{j}&a_{i+1}&\ldots &a_{n}\end{bmatrix}}=x_{i}\det(A)}$

где векторы являются столбцами матрицы A. Правило также подразумевается тождеством ${\displaystyle a_{j}}$

${\displaystyle A\,\operatorname {adj} (A)=\operatorname {adj} (A)\,A=\det(A)\,I_{n}.}$

Правило Крамера может быть реализовано со временем, что сопоставимо с более распространенными методами решения систем линейных уравнений, такими как LU , QR или сингулярное разложение . ^[37] ${\displaystyle \operatorname {O} (n^{3})}$

Линейная независимость

Определители могут быть использованы для характеристики линейно зависимых векторов: равен нулю тогда и только тогда, когда векторы-столбцы (или, что эквивалентно, векторы-строки) матрицы линейно зависимы. ^[38] Например, если заданы два линейно независимых вектора , третий вектор лежит в плоскости, охватываемой первыми двумя векторами, точно тогда, когда определитель -матрицы, состоящей из трех векторов, равен нулю. Та же идея используется и в теории дифференциальных уравнений : заданы функции (предполагается, что они дифференцируемы по времени ), вронскиан определяется как ${\displaystyle \det A}$ ${\displaystyle A}$ ${\displaystyle v_{1},v_{2}\in \mathbf {R} ^{3}}$ ${\displaystyle v_{3}}$ ${\displaystyle 3\times 3}$ ${\displaystyle f_{1}(x),\dots ,f_{n}(x)}$ ${\displaystyle n-1}$

${\displaystyle W(f_{1},\ldots ,f_{n})(x)={\begin{vmatrix}f_{1}(x)&f_{2}(x)&\cdots &f_{n}(x)\\f_{1}'(x)&f_{2}'(x)&\cdots &f_{n}'(x)\\\vdots &\vdots &\ddots &\vdots \\f_{1}^{(n-1)}(x)&f_{2}^{(n-1)}(x)&\cdots &f_{n}^{(n-1)}(x)\end{vmatrix}}.}$

Он не равен нулю (для некоторых ) в указанном интервале тогда и только тогда, когда заданные функции и все их производные вплоть до порядка линейно независимы. Если можно показать, что вронскиан равен нулю всюду на интервале, то в случае аналитических функций это означает, что заданные функции линейно зависимы. См. Вронскиан и линейная независимость . Другое такое использование определителя — результант , который дает критерий, когда два многочлена имеют общий корень . ^[39] ${\displaystyle x}$ ${\displaystyle n-1}$

Ориентация основы

Определитель можно рассматривать как присвоение числа каждой последовательности из n векторов в R ⁿ , используя квадратную матрицу, столбцы которой являются заданными векторами. Определитель будет ненулевым тогда и только тогда, когда последовательность векторов является базисом для R n ^. В этом случае знак определителя определяет, согласуется ли ориентация базиса с ориентацией стандартного базиса или противоположна ей . В случае ортогонального базиса величина определителя равна произведению длин базисных векторов. Например, ортогональная матрица с элементами в R ⁿ представляет собой ортонормированный базис в евклидовом пространстве и, следовательно, имеет определитель ±1 (так как все векторы имеют длину 1). Определитель равен +1 тогда и только тогда, когда базис имеет ту же ориентацию. Он равен −1 тогда и только тогда, когда базис имеет противоположную ориентацию.

В более общем случае, если определитель A положителен, то A представляет собой сохраняющее ориентацию линейное преобразование (если A — ортогональная матрица 2 × 2 или 3 × 3 , то это поворот ), а если он отрицателен, то A меняет ориентацию базиса.

Объем и определитель Якобиана

Как указано выше, абсолютное значение определителя действительных векторов равно объему параллелепипеда, охватываемого этими векторами. Как следствие, если — линейная карта, заданная умножением на матрицу , и — любое измеримое подмножество , то объем задается умножением на объем . ^[40] В более общем случае, если линейная карта представлена ​​-матрицей , то -мерный объем задается как: ${\displaystyle f:\mathbf {R} ^{n}\to \mathbf {R} ^{n}}$ ${\displaystyle A}$ ${\displaystyle S\subset \mathbf {R} ^{n}}$ ${\displaystyle f(S)}$ ${\displaystyle |\det(A)|}$ ${\displaystyle S}$ ${\displaystyle f:\mathbf {R} ^{n}\to \mathbf {R} ^{m}}$ ${\displaystyle m\times n}$ ${\displaystyle A}$ ${\displaystyle n}$ ${\displaystyle f(S)}$

${\displaystyle \operatorname {volume} (f(S))={\sqrt {\det \left(A^{\textsf {T}}A\right)}}\operatorname {volume} (S).}$

Вычислив объем тетраэдра, ограниченного четырьмя точками, их можно использовать для определения скрещивающихся линий . Объем любого тетраэдра, учитывая его вершины , или любую другую комбинацию пар вершин, которые образуют остовное дерево над вершинами. ${\displaystyle a,b,c,d}$ ${\displaystyle {\frac {1}{6}}\cdot |\det(a-b,b-c,c-d)|}$

Нелинейное отображение отправляет небольшой квадрат (слева, в красном) в искаженный параллелограмм (справа, в красном). Якобиан в точке дает наилучшее линейное приближение искаженного параллелограмма вблизи этой точки (справа, в полупрозрачном белом), а определитель Якобиана дает отношение площади аппроксимирующего параллелограмма к площади исходного квадрата. ${\displaystyle f\colon \mathbf {R} ^{2}\to \mathbf {R} ^{2}}$

Для общей дифференцируемой функции многое из вышесказанного переносится при рассмотрении матрицы Якоби функции f . Для

${\displaystyle f:\mathbf {R} ^{n}\rightarrow \mathbf {R} ^{n},}$

Матрица Якоби — это матрица n × n , элементы которой задаются частными производными

${\displaystyle D(f)=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{1\leq i,j\leq n}.}$

Его определитель, определитель Якоби , появляется в многомерной версии интегрирования путем подстановки : для подходящих функций f и открытого подмножества U R ⁿ (области определения f ) интеграл по f ( U ) некоторой другой функции φ  : R ⁿ → R ^m определяется как

${\displaystyle \int _{f(U)}\phi (\mathbf {v} )\,d\mathbf {v} =\int _{U}\phi (f(\mathbf {u} ))\left|\det(\operatorname {D} f)(\mathbf {u} )\right|\,d\mathbf {u} .}$

Якобиан также встречается в теореме об обратной функции .

Применительно к области картографии определитель можно использовать для измерения скорости расширения карты вблизи полюсов. ^[41]

Абстрактные алгебраические аспекты

Определитель эндоморфизма

Вышеуказанные тождества, касающиеся определителя произведений и обратных матриц, подразумевают, что подобные матрицы имеют одинаковый определитель: две матрицы A и B подобны, если существует обратимая матрица X такая, что A = X ⁻¹ BX . Действительно, многократное применение приведенных выше тождеств дает

${\displaystyle \det(A)=\det(X)^{-1}\det(B)\det(X)=\det(B)\det(X)^{-1}\det(X)=\det(B).}$

Определитель поэтому также называется инвариантом подобия . Определитель линейного преобразования

${\displaystyle T:V\to V}$

для некоторого конечномерного векторного пространства V определяется как определитель описывающей его матрицы относительно произвольного выбора базиса в V. В силу инвариантности подобия этот определитель не зависит от выбора базиса для V и, следовательно , зависит только от эндоморфизма T.

Квадратные матрицы над коммутативными кольцами

Вышеприведенное определение определителя с использованием правила Лейбница работает более общо, когда элементы матрицы являются элементами коммутативного кольца , например, целыми числами , в отличие от поля действительных или комплексных чисел. Более того, характеристика определителя как уникального чередующегося полилинейного отображения, которое удовлетворяет , все еще сохраняется, как и все свойства, вытекающие из этой характеристики. ^[42] ${\displaystyle R}$ ${\displaystyle \mathbf {Z} }$ ${\displaystyle \det(I)=1}$

Матрица обратима (в том смысле, что существует обратная матрица, элементы которой находятся в ) тогда и только тогда, когда ее определитель является обратимым элементом в . ^[43] Для это означает, что определитель равен +1 или −1. Такая матрица называется унимодулярной . ${\displaystyle A\in \operatorname {Mat} _{n\times n}(R)}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle R=\mathbf {Z} }$

Определитель является мультипликативным, он определяет гомоморфизм групп

${\displaystyle \operatorname {GL} _{n}(R)\rightarrow R^{\times },}$

между общей линейной группой (группой обратимых -матриц с элементами в ) и мультипликативной группой единиц в . Поскольку оно уважает умножение в обеих группах, это отображение является групповым гомоморфизмом . ${\displaystyle n\times n}$ ${\displaystyle R}$ ${\displaystyle R}$

Определитель — это естественное преобразование.

При наличии гомоморфизма колец существует отображение, заданное заменой всех записей в их образами при . Определитель соблюдает эти отображения, т.е. тождество ${\displaystyle f:R\to S}$ ${\displaystyle \operatorname {GL} _{n}(f):\operatorname {GL} _{n}(R)\to \operatorname {GL} _{n}(S)}$ ${\displaystyle R}$ ${\displaystyle f}$

${\displaystyle f(\det((a_{i,j})))=\det((f(a_{i,j})))}$

выполняется. Другими словами, отображаемая коммутативная диаграмма коммутирует.

Например, определитель комплексно сопряженной комплексной матрицы (который также является определителем ее сопряженного транспонирования) является комплексно сопряженным ее определителем, а для целочисленных матриц: модуль приведения определителя такой матрицы равен определителю матрицы, приведенной по модулю (последний определитель вычисляется с использованием модульной арифметики ). На языке теории категорий определитель является естественным преобразованием между двумя функторами и . ^[44] Добавляя еще один уровень абстракции, это фиксируется, говоря, что определитель является морфизмом алгебраических групп , из общей линейной группы в мультипликативную группу , ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle \operatorname {GL} _{n}}$ ${\displaystyle (-)^{\times }}$

${\displaystyle \det :\operatorname {GL} _{n}\to \mathbb {G} _{m}.}$

Внешняя алгебра

The determinant of a linear transformation ${\displaystyle T:V\to V}$ of an ${\displaystyle n}$-dimensional vector space ${\displaystyle V}$ or, more generally a free module of (finite) rank ${\displaystyle n}$ over a commutative ring ${\displaystyle R}$ can be formulated in a coordinate-free manner by considering the ${\displaystyle n}$-th exterior power ${\displaystyle \bigwedge ^{n}V}$ of ${\displaystyle V}$.^[45] The map ${\displaystyle T}$ induces a linear map

${\displaystyle {\begin{aligned}\bigwedge ^{n}T:\bigwedge ^{n}V&\rightarrow \bigwedge ^{n}V\\v_{1}\wedge v_{2}\wedge \dots \wedge v_{n}&\mapsto Tv_{1}\wedge Tv_{2}\wedge \dots \wedge Tv_{n}.\end{aligned}}}$

As ${\displaystyle \bigwedge ^{n}V}$ is one-dimensional, the map ${\displaystyle \bigwedge ^{n}T}$ is given by multiplying with some scalar, i.e., an element in ${\displaystyle R}$. Some authors such as (Bourbaki 1998) use this fact to define the determinant to be the element in ${\displaystyle R}$ satisfying the following identity (for all ${\displaystyle v_{i}\in V}$):

${\displaystyle \left(\bigwedge ^{n}T\right)\left(v_{1}\wedge \dots \wedge v_{n}\right)=\det(T)\cdot v_{1}\wedge \dots \wedge v_{n}.}$

This definition agrees with the more concrete coordinate-dependent definition. This can be shown using the uniqueness of a multilinear alternating form on ${\displaystyle n}$-tuples of vectors in ${\displaystyle R^{n}}$. For this reason, the highest non-zero exterior power ${\displaystyle \bigwedge ^{n}V}$ (as opposed to the determinant associated to an endomorphism) is sometimes also called the determinant of ${\displaystyle V}$ and similarly for more involved objects such as vector bundles or chain complexes of vector spaces. Minors of a matrix can also be cast in this setting, by considering lower alternating forms ${\displaystyle \bigwedge ^{k}V}$ with ${\displaystyle k<n}$.^[46]

Generalizations and related notions

Determinants as treated above admit several variants: the permanent of a matrix is defined as the determinant, except that the factors ${\displaystyle \operatorname {sgn}(\sigma )}$ occurring in Leibniz's rule are omitted. The immanant generalizes both by introducing a character of the symmetric group ${\displaystyle S_{n}}$ in Leibniz's rule.

Determinants for finite-dimensional algebras

For any associative algebra ${\displaystyle A}$ that is finite-dimensional as a vector space over a field ${\displaystyle F}$, there is a determinant map^[47]

${\displaystyle \det :A\to F.}$

This definition proceeds by establishing the characteristic polynomial independently of the determinant, and defining the determinant as the lowest order term of this polynomial. This general definition recovers the determinant for the matrix algebra ${\displaystyle A=\operatorname {Mat} _{n\times n}(F)}$, but also includes several further cases including the determinant of a quaternion,

${\displaystyle \det(a+ib+jc+kd)=a^{2}+b^{2}+c^{2}+d^{2}}$,

the norm ${\displaystyle N_{L/F}:L\to F}$ of a field extension, as well as the Pfaffian of a skew-symmetric matrix and the reduced norm of a central simple algebra, also arise as special cases of this construction.

Infinite matrices

For matrices with an infinite number of rows and columns, the above definitions of the determinant do not carry over directly. For example, in the Leibniz formula, an infinite sum (all of whose terms are infinite products) would have to be calculated. Functional analysis provides different extensions of the determinant for such infinite-dimensional situations, which however only work for particular kinds of operators.

The Fredholm determinant defines the determinant for operators known as trace class operators by an appropriate generalization of the formula

${\displaystyle \det(I+A)=\exp(\operatorname {tr} (\log(I+A))).}$

Another infinite-dimensional notion of determinant is the functional determinant.

Operators in von Neumann algebras

For operators in a finite factor, one may define a positive real-valued determinant called the Fuglede−Kadison determinant using the canonical trace. In fact, corresponding to every tracial state on a von Neumann algebra there is a notion of Fuglede−Kadison determinant.

Related notions for non-commutative rings

For matrices over non-commutative rings, multilinearity and alternating properties are incompatible for n ≥ 2,^[48] so there is no good definition of the determinant in this setting.

For square matrices with entries in a non-commutative ring, there are various difficulties in defining determinants analogously to that for commutative rings. A meaning can be given to the Leibniz formula provided that the order for the product is specified, and similarly for other definitions of the determinant, but non-commutativity then leads to the loss of many fundamental properties of the determinant, such as the multiplicative property or that the determinant is unchanged under transposition of the matrix. Over non-commutative rings, there is no reasonable notion of a multilinear form (existence of a nonzero bilinear form^[clarify] with a regular element of R as value on some pair of arguments implies that R is commutative). Nevertheless, various notions of non-commutative determinant have been formulated that preserve some of the properties of determinants, notably quasideterminants and the Dieudonné determinant. For some classes of matrices with non-commutative elements, one can define the determinant and prove linear algebra theorems that are very similar to their commutative analogs. Examples include the q-determinant on quantum groups, the Capelli determinant on Capelli matrices, and the Berezinian on supermatrices (i.e., matrices whose entries are elements of ${\displaystyle \mathbb {Z} _{2}}$-graded rings).^[49] Manin matrices form the class closest to matrices with commutative elements.

Calculation

Determinants are mainly used as a theoretical tool. They are rarely calculated explicitly in numerical linear algebra, where for applications such as checking invertibility and finding eigenvalues the determinant has largely been supplanted by other techniques.^[50] Computational geometry, however, does frequently use calculations related to determinants.^[51]

While the determinant can be computed directly using the Leibniz rule this approach is extremely inefficient for large matrices, since that formula requires calculating ${\displaystyle n!}$ ( ${\displaystyle n}$ factorial) products for an ${\displaystyle n\times n}$-matrix. Thus, the number of required operations grows very quickly: it is of order ${\displaystyle n!}$. The Laplace expansion is similarly inefficient. Therefore, more involved techniques have been developed for calculating determinants.

Gaussian elemination

Gaussian elimination consists of left multiplying a matrix by elementary matrices for getting a matrix in a row echelon form. One can restrict the computation to elementary matrices of determinant 1. In this case, the determinant of the resulting row echelon form equals the determinant of the initial matrix. As a row echelon form is a triangular matrix, its determinant is the product of the entries of its diagonal.

So, the determinant can be computed for almost free from the result of a Gaussian elemination.

Decomposition methods

Some methods compute ${\displaystyle \det(A)}$ by writing the matrix as a product of matrices whose determinants can be more easily computed. Such techniques are referred to as decomposition methods. Examples include the LU decomposition, the QR decomposition or the Cholesky decomposition (for positive definite matrices). These methods are of order ${\displaystyle \operatorname {O} (n^{3})}$, which is a significant improvement over ${\displaystyle \operatorname {O} (n!)}$.^[52]

For example, LU decomposition expresses ${\displaystyle A}$ as a product

${\displaystyle A=PLU.}$

of a permutation matrix ${\displaystyle P}$ (which has exactly a single ${\displaystyle 1}$ in each column, and otherwise zeros), a lower triangular matrix ${\displaystyle L}$ and an upper triangular matrix ${\displaystyle U}$. The determinants of the two triangular matrices ${\displaystyle L}$ and ${\displaystyle U}$ can be quickly calculated, since they are the products of the respective diagonal entries. The determinant of ${\displaystyle P}$ is just the sign ${\displaystyle \varepsilon }$ of the corresponding permutation (which is ${\displaystyle +1}$ for an even number of permutations and is ${\displaystyle -1}$ for an odd number of permutations). Once such a LU decomposition is known for ${\displaystyle A}$, its determinant is readily computed as

${\displaystyle \det(A)=\varepsilon \det(L)\cdot \det(U).}$

Further methods

The order ${\displaystyle \operatorname {O} (n^{3})}$ reached by decomposition methods has been improved by different methods. If two matrices of order ${\displaystyle n}$ can be multiplied in time ${\displaystyle M(n)}$, where ${\displaystyle M(n)\geq n^{a}}$ for some ${\displaystyle a>2}$, then there is an algorithm computing the determinant in time ${\displaystyle O(M(n))}$.^[53] This means, for example, that an ${\displaystyle \operatorname {O} (n^{2.376})}$ algorithm for computing the determinant exists based on the Coppersmith–Winograd algorithm. This exponent has been further lowered, as of 2016, to 2.373.^[54]

In addition to the complexity of the algorithm, further criteria can be used to compare algorithms. Especially for applications concerning matrices over rings, algorithms that compute the determinant without any divisions exist. (By contrast, Gauss elimination requires divisions.) One such algorithm, having complexity ${\displaystyle \operatorname {O} (n^{4})}$ is based on the following idea: one replaces permutations (as in the Leibniz rule) by so-called closed ordered walks, in which several items can be repeated. The resulting sum has more terms than in the Leibniz rule, but in the process several of these products can be reused, making it more efficient than naively computing with the Leibniz rule.^[55] Algorithms can also be assessed according to their bit complexity, i.e., how many bits of accuracy are needed to store intermediate values occurring in the computation. For example, the Gaussian elimination (or LU decomposition) method is of order ${\displaystyle \operatorname {O} (n^{3})}$, but the bit length of intermediate values can become exponentially long.^[56] By comparison, the Bareiss Algorithm, is an exact-division method (so it does use division, but only in cases where these divisions can be performed without remainder) is of the same order, but the bit complexity is roughly the bit size of the original entries in the matrix times ${\displaystyle n}$.^[57]

If the determinant of A and the inverse of A have already been computed, the matrix determinant lemma allows rapid calculation of the determinant of A + uv^T, where u and v are column vectors.

Charles Dodgson (i.e. Lewis Carroll of Alice's Adventures in Wonderland fame) invented a method for computing determinants called Dodgson condensation. Unfortunately this interesting method does not always work in its original form.^[58]

See also

• Mathematics portal

• Cauchy determinant
• Cayley–Menger determinant
• Dieudonné determinant
• Slater determinant
• Determinantal conjecture

Notes

1. Lang 1985, §VII.1
2. Wildberger, Norman J. (2010). Episode 4 (video lecture). WildLinAlg. Sydney, Australia: University of New South Wales. Archived from the original on 2021-12-11 – via YouTube.
3. "Determinants and Volumes". textbooks.math.gatech.edu. Retrieved 16 March 2018.
4. McConnell (1957). Applications of Tensor Analysis. Dover Publications. pp. 10–17.
5. Harris 2014, §4.7
6. Serge Lang, Linear Algebra, 2nd Edition, Addison-Wesley, 1971, pp 173, 191.
7. Lang 1987, §VI.7, Theorem 7.5
8. Alternatively, Bourbaki 1998, §III.8, Proposition 1 proves this result using the functoriality of the exterior power.
9. Horn & Johnson 2018, §0.8.7
10. Kung, Rota & Yan 2009, p. 306
11. Horn & Johnson 2018, §0.8.2.
12. Silvester, J. R. (2000). "Determinants of Block Matrices". Math. Gaz. 84 (501): 460–467. doi:10.2307/3620776. JSTOR 3620776. S2CID 41879675.
13. Sothanaphan, Nat (January 2017). "Determinants of block matrices with noncommuting blocks". Linear Algebra and Its Applications. 512: 202–218. arXiv:1805.06027. doi:10.1016/j.laa.2016.10.004. S2CID 119272194.
14. Proofs can be found in http://www.ee.ic.ac.uk/hp/staff/dmb/matrix/proof003.html
15. Lin, Minghua; Sra, Suvrit (2014). "Completely strong superadditivity of generalized matrix functions". arXiv:1410.1958 [math.FA].
16. Paksoy; Turkmen; Zhang (2014). "Inequalities of Generalized Matrix Functions via Tensor Products". Electronic Journal of Linear Algebra. 27: 332–341. doi:10.13001/1081-3810.1622.
17. Serre, Denis (Oct 18, 2010). "Concavity of det1/n over HPDn". MathOverflow.
18. Lang 1985, §VIII.2, Horn & Johnson 2018, Def. 1.2.3
19. Horn & Johnson 2018, Observation 7.1.2, Theorem 7.2.5
20. A proof can be found in the Appendix B of Kondratyuk, L. A.; Krivoruchenko, M. I. (1992). "Superconducting quark matter in SU(2) color group". Zeitschrift für Physik A. 344 (1): 99–115. Bibcode:1992ZPhyA.344...99K. doi:10.1007/BF01291027. S2CID 120467300.
21. Horn & Johnson 2018, § 0.8.10
22. Grattan-Guinness 2003, §6.6
23. Cajori, F. A History of Mathematics p. 80
24. Campbell, H: "Linear Algebra With Applications", pages 111–112. Appleton Century Crofts, 1971
25. Eves 1990, p. 405
26. A Brief History of Linear Algebra and Matrix Theory at: "A Brief History of Linear Algebra and Matrix Theory". Archived from the original on 10 September 2012. Retrieved 24 January 2012.
27. Kleiner 2007, p. 80
28. Bourbaki (1994, p. 59)
29. Muir, Sir Thomas, The Theory of Determinants in the historical Order of Development [London, England: Macmillan and Co., Ltd., 1906]. JFM 37.0181.02
30. Kleiner 2007, §5.2
31. The first use of the word "determinant" in the modern sense appeared in: Cauchy, Augustin-Louis "Memoire sur les fonctions qui ne peuvent obtenir que deux valeurs égales et des signes contraires par suite des transpositions operées entre les variables qu'elles renferment," which was first read at the Institute de France in Paris on November 30, 1812, and which was subsequently published in the Journal de l'Ecole Polytechnique, Cahier 17, Tome 10, pages 29–112 (1815).
32. Origins of mathematical terms: http://jeff560.tripod.com/d.html
33. History of matrices and determinants: http://www-history.mcs.st-and.ac.uk/history/HistTopics/Matrices_and_determinants.html
34. Eves 1990, p. 494
35. Cajori 1993, Vol. II, p. 92, no. 462
36. History of matrix notation: http://jeff560.tripod.com/matrices.html
37. Habgood & Arel 2012
38. Lang 1985, §VII.3
39. Lang 2002, §IV.8
40. Lang 1985, §VII.6, Theorem 6.10
41. Lay, David (2021). Linear Algebra and Its Applications 6th Edition. Pearson. p. 172.
42. Dummit & Foote 2004, §11.4
43. Dummit & Foote 2004, §11.4, Theorem 30
44. Mac Lane 1998, §I.4. See also Natural transformation § Determinant.
45. Bourbaki 1998, §III.8
46. Lombardi & Quitté 2015, §5.2, Bourbaki 1998, §III.5
47. Garibaldi 2004
48. In a non-commutative setting left-linearity (compatibility with left-multiplication by scalars) should be distinguished from right-linearity. Assuming linearity in the columns is taken to be left-linearity, one would have, for non-commuting scalars a, b: $${\displaystyle {\begin{aligned}ab&=ab{\begin{vmatrix}1&0\\0&1\end{vmatrix}}=a{\begin{vmatrix}1&0\\0&b\end{vmatrix}}\\[5mu]&={\begin{vmatrix}a&0\\0&b\end{vmatrix}}=b{\begin{vmatrix}a&0\\0&1\end{vmatrix}}=ba{\begin{vmatrix}1&0\\0&1\end{vmatrix}}=ba,\end{aligned}}}$$a contradiction. There is no useful notion of multi-linear functions over a non-commutative ring.
49. Varadarajan, V. S (2004), Supersymmetry for mathematicians: An introduction, American Mathematical Soc., ISBN 978-0-8218-3574-6.
50. "... we mention that the determinant, though a convenient notion theoretically, rarely finds a useful role in numerical algorithms.", see Trefethen & Bau III 1997, Lecture 1.
51. Fisikopoulos & Peñaranda 2016, §1.1, §4.3
52. Camarero, Cristóbal (2018-12-05). "Simple, Fast and Practicable Algorithms for Cholesky, LU and QR Decomposition Using Fast Rectangular Matrix Multiplication". arXiv:1812.02056 [cs.NA].
53. Bunch & Hopcroft 1974
54. Fisikopoulos & Peñaranda 2016, §1.1
55. Rote 2001
56. Fang, Xin Gui; Havas, George (1997). "On the worst-case complexity of integer Gaussian elimination" (PDF). Proceedings of the 1997 international symposium on Symbolic and algebraic computation. ISSAC '97. Kihei, Maui, Hawaii, United States: ACM. pp. 28–31. doi:10.1145/258726.258740. ISBN 0-89791-875-4. Archived from the original (PDF) on 2011-08-07. Retrieved 2011-01-22.
57. Fisikopoulos & Peñaranda 2016, §1.1, Bareiss 1968
58. Abeles, Francine F. (2008). "Dodgson condensation: The historical and mathematical development of an experimental method". Linear Algebra and Its Applications. 429 (2–3): 429–438. doi:10.1016/j.laa.2007.11.022.

References

• Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
• Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
• Bareiss, Erwin (1968), "Sylvester's Identity and Multistep Integer-Preserving Gaussian Elimination" (PDF), Mathematics of Computation, 22 (102): 565–578, doi:10.2307/2004533, JSTOR 2004533, archived (PDF) from the original on 2012-10-25
• de Boor, Carl (1990), "An empty exercise" (PDF), ACM SIGNUM Newsletter, 25 (2): 3–7, doi:10.1145/122272.122273, S2CID 62780452, archived (PDF) from the original on 2006-09-01
• Bourbaki, Nicolas (1998), Algebra I, Chapters 1-3, Springer, ISBN 9783540642435
• Bunch, J. R.; Hopcroft, J. E. (1974). "Triangular Factorization and Inversion by Fast Matrix Multiplication". Mathematics of Computation. 28 (125): 231–236. doi:10.1090/S0025-5718-1974-0331751-8. hdl:1813/6003.
• Dummit, David S.; Foote, Richard M. (2004), Abstract algebra (3rd ed.), Hoboken, NJ: Wiley, ISBN 9780471452348, OCLC 248917264
• Fisikopoulos, Vissarion; Peñaranda, Luis (2016), "Faster geometric algorithms via dynamic determinant computation", Computational Geometry, 54: 1–16, arXiv:1206.7067, doi:10.1016/j.comgeo.2015.12.001
• Garibaldi, Skip (2004), "The characteristic polynomial and determinant are not ad hoc constructions", American Mathematical Monthly, 111 (9): 761–778, arXiv:math/0203276, doi:10.2307/4145188, JSTOR 4145188, MR 2104048
• Habgood, Ken; Arel, Itamar (2012). "A condensation-based application of Cramer's rule for solving large-scale linear systems" (PDF). Journal of Discrete Algorithms. 10: 98–109. doi:10.1016/j.jda.2011.06.007. Archived (PDF) from the original on 2019-05-05.
• Harris, Frank E. (2014), Mathematics for Physical Science and Engineering, Elsevier, ISBN 9780128010495
• Kleiner, Israel (2007), Kleiner, Israel (ed.), A history of abstract algebra, Birkhäuser, doi:10.1007/978-0-8176-4685-1, ISBN 978-0-8176-4684-4, MR 2347309
• Kung, Joseph P.S.; Rota, Gian-Carlo; Yan, Catherine (2009), Combinatorics: The Rota Way, Cambridge University Press, ISBN 9780521883894
• Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7
• Lombardi, Henri; Quitté, Claude (2015), Commutative Algebra: Constructive Methods, Springer, ISBN 9789401799447
• Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics 5 (2nd ed.), Springer-Verlag, ISBN 0-387-98403-8
• Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8, archived from the original on 2009-10-31
• Muir, Thomas (1960) [1933], A treatise on the theory of determinants, Revised and enlarged by William H. Metzler, New York, NY: Dover
• Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3
• G. Baley Price (1947) "Some identities in the theory of determinants", American Mathematical Monthly 54:75–90 MR0019078
• Horn, Roger Alan; Johnson, Charles Royal (2018) [1985]. Matrix Analysis (2nd ed.). Cambridge University Press. ISBN 978-0-521-54823-6.
• Lang, Serge (1985), Introduction to Linear Algebra, Undergraduate Texts in Mathematics (2 ed.), Springer, ISBN 9780387962054
• Lang, Serge (1987), Linear Algebra, Undergraduate Texts in Mathematics (3 ed.), Springer, ISBN 9780387964126
• Lang, Serge (2002). Algebra. Graduate Texts in Mathematics. New York, NY: Springer. ISBN 978-0-387-95385-4.
• Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall
• Rote, Günter (2001), "Division-free algorithms for the determinant and the Pfaffian: algebraic and combinatorial approaches" (PDF), Computational discrete mathematics, Lecture Notes in Comput. Sci., vol. 2122, Springer, pp. 119–135, doi:10.1007/3-540-45506-X_9, ISBN 978-3-540-42775-9, MR 1911585, archived from the original (PDF) on 2007-02-01, retrieved 2020-06-04
• Trefethen, Lloyd; Bau III, David (1997), Numerical Linear Algebra (1st ed.), Philadelphia: SIAM, ISBN 978-0-89871-361-9

Historical references

• Bourbaki, Nicolas (1994), Elements of the history of mathematics, translated by Meldrum, John, Springer, doi:10.1007/978-3-642-61693-8, ISBN 3-540-19376-6
• Cajori, Florian (1993), A history of mathematical notations: Including Vol. I. Notations in elementary mathematics; Vol. II. Notations mainly in higher mathematics, Reprint of the 1928 and 1929 originals, Dover, ISBN 0-486-67766-4, MR 3363427
• Bézout, Étienne (1779), Théorie générale des equations algébriques, Paris
• Cayley, Arthur (1841), "On a theorem in the geometry of position", Cambridge Mathematical Journal, 2: 267–271
• Cramer, Gabriel (1750), Introduction à l'analyse des lignes courbes algébriques, Genève: Frères Cramer & Cl. Philibert, doi:10.3931/e-rara-4048
• Eves, Howard (1990), An introduction to the history of mathematics (6 ed.), Saunders College Publishing, ISBN 0-03-029558-0, MR 1104435
• Grattan-Guinness, I., ed. (2003), Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences, vol. 1, Johns Hopkins University Press, ISBN 9780801873966
• Jacobi, Carl Gustav Jakob (1841), "De Determinantibus functionalibus", Journal für die reine und angewandte Mathematik, 1841 (22): 320–359, doi:10.1515/crll.1841.22.319, S2CID 123637858
• Laplace, Pierre-Simon, de (1772), "Recherches sur le calcul intégral et sur le systéme du monde", Histoire de l'Académie Royale des Sciences (seconde partie), Paris: 267–376{{citation}}: CS1 maint: multiple names: authors list (link)

External links

• Suprunenko, D.A. (2001) [1994], "Determinant", Encyclopedia of Mathematics, EMS Press
• Weisstein, Eric W. "Determinant". MathWorld.
• O'Connor, John J.; Robertson, Edmund F., "Matrices and determinants", MacTutor History of Mathematics Archive, University of St Andrews
• Determinant Interactive Program and Tutorial
• Linear algebra: determinants. Archived 2008-12-04 at the Wayback Machine Compute determinants of matrices up to order 6 using Laplace expansion you choose.
• Determinant Calculator Calculator for matrix determinants, up to the 8th order.
• Matrices and Linear Algebra on the Earliest Uses Pages
• Determinants explained in an easy fashion in the 4th chapter as a part of a Linear Algebra course.