История математической нотации

Происхождение и эволюция символов, используемых для записи уравнений и формул

История математической нотации ^[1] включает в себя начало, развитие и культурную диффузию математических символов и конфликт методов нотации, с которыми столкнулись при движении нотации к популярности или незаметности. Математическая нотация ^[2] включает в себя символы, используемые для записи математических уравнений и формул . Нотация, как правило, подразумевает набор четко определенных представлений величин и символов-операторов. ^[3] История включает в себя индо-арабские цифры , буквы римского , греческого , еврейского и немецкого алфавитов , а также множество символов, изобретенных математиками за последние несколько столетий.

Развитие математической нотации можно разделить на этапы: ^{[4] [5]}

• « Риторический » этап — это этап, на котором вычисления выполняются словами, без использования символов. ^[6]
• « Синкопированная » стадия — это стадия, на которой часто используемые операции и величины представлены символическими синтаксическими сокращениями. В античности и средневековье всплески математического творчества часто сменялись столетиями застоя. С началом раннего Нового времени и началом всемирного распространения знаний появились письменные примеры математических разработок.
• « Символическая » стадия — это когда всеобъемлющие системы обозначений заменяют риторику. Начиная с Италии в XVI веке, новые математические разработки, взаимодействующие с новыми научными открытиями, делались все более быстрыми темпами, которые продолжаются и по сей день. Эта символическая система использовалась средневековыми индийскими математиками и в Европе с середины XVII века ^[7] и продолжает развиваться в современную эпоху .

Область изучения, известная как история математики, в первую очередь занимается исследованием происхождения открытий в математике, и основное внимание здесь уделяется исследованию математических методов и обозначений прошлого.

Риторическая стадия

Хотя история начинается с ионических школ, нет сомнений, что те древние греки, которые обратили на нее внимание, были во многом обязаны предыдущим исследованиям древних египтян и древних финикийцев . Отличительная черта числовой нотации, т. е. символы, имеющие как локальные, так и внутренние значения ( арифметика ), подразумевает состояние цивилизации в период ее изобретения. Наши знания о математических достижениях этих ранних народов, которым посвящен этот раздел, несовершенны, и следующие краткие заметки следует рассматривать как резюме выводов, которые кажутся наиболее вероятными, а история математики начинается с символических разделов.

Многие области математики начинались с изучения реальных проблем , до того как основные правила и концепции были идентифицированы и определены как абстрактные структуры . Например, геометрия берет свое начало в вычислении расстояний и площадей в реальном мире; алгебра начиналась с методов решения задач в арифметике .

Не может быть никаких сомнений в том, что большинство древних народов, оставивших записи, знали что-то о нумерации и механике , а некоторые были также знакомы с элементами землемерия . В частности, египтяне уделяли внимание геометрии и числам, а финикийцы — практической арифметике, бухгалтерскому учету , навигации и землемерию. Результаты, достигнутые этими людьми, по-видимому, были доступны при определенных условиях путешественникам. Вероятно, что знания египтян и финикийцев были в значительной степени результатом наблюдений и измерений и представляли собой накопленный опыт многих веков.

Начало записи

Вавилонская табличка (ок. 1800–1600 гг. до н. э.), на которой показано приближение квадратного корня из 2 (1 24 51 10 w: шестидесятеричная ) в контексте теоремы Пифагора для равнобедренного треугольника .

Письменная математика началась с чисел, выраженных в виде меток счета , где каждая метка представляла одну единицу. Числовые символы, вероятно, состояли из штрихов или зарубок, вырезанных на дереве или камне, и были понятны всем народам. Например, одна зарубка на кости представляла одно животное, или человека, или что-либо еще. Народы, с которыми греки Малой Азии (среди которых начинается запись в западной истории), вероятно, часто вступали в контакт, были народами, населявшими восточное побережье Средиземного моря: и греческая традиция единогласно приписывала особое развитие геометрии египтянам, а науку о числах — либо египтянам, либо финикийцам.

У древних египтян была символическая нотация, которая представляла собой нумерацию иероглифами . ^{[8] [9]} В египетской математике был символ для одного, десяти, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона. Меньшие цифры располагались слева от числа, как и в индо-арабских цифрах. Позже египтяне использовали иератическое письмо вместо иероглифического для отображения чисел. Иератическое письмо было больше похоже на курсив и заменяло несколько групп символов отдельными. Например, четыре вертикальные линии, используемые для представления числа четыре, были заменены одной горизонтальной линией. Это можно найти в математическом папирусе Райнда (ок. 2000–1800 гг. до н. э.) и Московском математическом папирусе (ок. 1890 г. до н. э.). Система, которую использовали египтяне, была открыта и изменена многими другими цивилизациями Средиземноморья. У египтян также были символы для основных операций: ноги, идущие вперед, представляли сложение, а ноги, идущие назад, представляли вычитание.

У жителей Месопотамии были символы для каждой степени числа десять. ^[10] Позже они записывали свои числа почти точно так же, как это делается в наше время. Вместо того, чтобы иметь символы для каждой степени числа десять, они просто ставили коэффициент этого числа. Каждая цифра была отделена только пробелом, но ко времени Александра Македонского они создали символ, который представлял ноль и был заполнителем. Жители Месопотамии также использовали шестидесятеричную систему счисления, то есть с основанием шестьдесят. Именно эта система используется в наше время при измерении времени и углов. Вавилонская математика происходит из более чем 400 глиняных табличек, найденных с 1850-х годов. ^[11] Написанные клинописью , таблички были написаны, пока глина была влажной, и затвердевали в печи или под воздействием солнечного тепла. Некоторые из них, по-видимому, были оцененными домашними заданиями. Самые ранние свидетельства письменной математики восходят к древним шумерам и системе метрологии с 3000 года до нашей эры. Начиная примерно с 2500 г. до н. э. шумеры писали таблицы умножения на глиняных табличках и решали геометрические упражнения и задачи на деление . Самые ранние следы вавилонских цифр также относятся к этому периоду. ^[12]

Большинство месопотамских глиняных табличек датируются периодом с 1800 по 1600 год до нашей эры и охватывают темы, которые включают дроби, алгебру, квадратные и кубические уравнения, а также вычисление регулярных , обратных и парных чисел . ^[13] Таблички также включают таблицы умножения и методы решения линейных и квадратных уравнений . Вавилонская табличка YBC 7289 дает приближение √ 2 , которое является точным до эквивалента шести десятичных знаков. Вавилонская математика была записана с использованием шестидесятеричной (основание-60) системы счисления . Из этого вытекает современное использование 60 секунд в минуте, 60 минут в часе и 360 (60 × 6) градусов в окружности, а также использование минут и секунд дуги для обозначения долей градуса. Вавилонские достижения в математике были облегчены тем фактом, что 60 имеет много делителей: обратная величина любого целого числа, кратного делителям 60, имеет конечное разложение по основанию 60. (В десятичной арифметике только обратные величины кратных 2 и 5 имеют конечное разложение в десятичной системе.) Кроме того, в отличие от египтян, греков и римлян, у вавилонян была настоящая позиционная система, где цифры, записанные в левом столбце, представляли большие значения, как и в десятичной системе. Однако у них не было эквивалента десятичной точки, и поэтому позиционное значение символа часто приходилось выводить из контекста.

Риторическая алгебра была впервые разработана древними вавилонянами и оставалась доминирующей вплоть до XVI века. В этой системе уравнения записываются полными предложениями. Например, риторическая форма — «Вещь плюс один равно двум» или, возможно, «Вещь плюс 1 равно 2». ${\displaystyle x+1=2}$

Синкопированная сцена

Смерть Архимеда , картина 1815 года Томаса Деджорджа . Последние слова, приписываемые Архимеду , — « Не тревожь мои круги », ссылка на круги на математическом чертеже, который он изучал, когда их потревожил римский солдат.

Историю математики нельзя с уверенностью проследить до какой-либо школы или периода до ионийских греков. Тем не менее, последующую историю можно разделить на периоды, различия между которыми достаточно хорошо обозначены. Греческая математика, которая возникла с изучением геометрии, имела тенденцию быть дедуктивной и научной с самого начала. С четвертого века нашей эры Пифагору обычно приписывают открытие теоремы Пифагора , теоремы в геометрии, которая гласит, что в прямоугольном треугольнике площадь квадрата на гипотенузе (стороне, противолежащей прямому углу) равна сумме площадей квадратов двух других сторон. ^[14] Древние математические тексты доступны с ранее упомянутыми древнеегипетскими обозначениями и с Plimpton 322 , вавилонской математикой около 1900 г. до н. э. Изучение математики как самостоятельного предмета началось в VI веке до нашей эры с пифагорейцев , которые ввели термин «математика» от древнегреческого μάθημα ( mathema ), что означает «предмет обучения». ^[15]

Влияние Платона было особенно сильным в математике и науках. Он помог провести различие между чистой и прикладной математикой , расширив разрыв между «арифметикой», теперь называемой теорией чисел , и «логистикой», теперь называемой арифметикой . Греческая математика значительно усовершенствовала методы (особенно посредством введения дедуктивного рассуждения и математической строгости в доказательствах ) и расширила предмет математики. ^[16] Аристотелю приписывают то, что позже назовут законом исключенного третьего .

Абстрактная или чистая математика ^[17] имеет дело с такими понятиями, как величина и количество, безотносительно к какому-либо практическому применению или ситуации, и включает арифметику и геометрию . Напротив, в смешанной или прикладной математике математические свойства и отношения применяются к объектам реального мира для моделирования законов физики, например, в гидростатике , оптике и навигации . ^[17]

Архимед, как правило, считается величайшим математиком древности и одним из величайших математиков всех времен. ^{[18] [19]} Он использовал метод исчерпывания для вычисления площади под дугой параболы с суммированием бесконечного ряда и дал удивительно точное приближение числа π . ^[20] Он также определил спираль , носящую его имя, формулы для объемов поверхностей вращения и гениальную систему для выражения очень больших чисел.

Предложения 31, 32 и 33 в девятой книге « Начал» Евклида , расположенной во 2-м томе рукописи, листы 207–208 лицевая сторона.

В историческом развитии геометрии шаги в абстракции геометрии были сделаны древними греками. «Начала» Евклида являются самой ранней сохранившейся документацией аксиом планиметрии — хотя Прокл рассказывает о более ранней аксиоматизации Гиппократом Хиосским . ^[21] «Начала » Евклида (ок. 300 г. до н. э.) являются одним из старейших сохранившихся греческих математических трактатов и состоят из 13 книг, написанных в Александрии; собирают теоремы, доказанные другими математиками, дополненные некоторыми оригинальными работами. Документ представляет собой удачный сборник определений, постулатов (аксиом), предложений (теорем и конструкций) и математических доказательств предложений. Первая теорема Евклида — это лемма , которая обладает свойствами простых чисел . Влиятельные тринадцать книг охватывают евклидову геометрию, геометрическую алгебру и древнегреческую версию алгебраических систем и элементарной теории чисел. Он был вездесущ в Квадривиуме и сыграл важную роль в развитии логики, математики и науки. « О движущейся сфере » Автолика — еще одна древняя математическая рукопись того времени. ^{[ требуется ссылка ]}

Следующим этапом обозначений для алгебры стала синкопированная алгебра, в которой используется некоторая символика, но которая не содержит всех характеристик символической алгебры. Например, может быть ограничение, что вычитание может быть использовано только один раз в пределах одной стороны уравнения, что не относится к символической алгебре. Синкопированное алгебраическое выражение впервые появилось в серии книг под названием «Арифметика » Диофанта Александрийского (III в. н. э., многие утрачены), за которой последовала « Брахма Спхута Сиддханта » Брахмагупты (VII в.).

Акрофоническая и милетская нумерация

Греки использовали аттическую систему счисления [ ^22] , которая была основана на системе египтян и позже была адаптирована и использована римлянами . Греческие цифры от одного до четырех были вертикальными линиями, как в иероглифах. Символом для пяти была греческая буква Π (пи), которая является буквой греческого слова для пяти, pente . Числа от шести до девяти были pente с вертикальными линиями рядом с ней. Десять была представлена ​​буквой (Δ) слова для десяти, deka , сто — буквой из слова для сотни и т. д.

Ионийская нумерация использовала весь их алфавит, включая три архаичные буквы. Цифровая нотация греков, хотя и была гораздо менее удобной, чем та, что используется сейчас, была сформирована по совершенно регулярному и научному плану ^[23] и могла использоваться с приемлемым эффектом в качестве инструмента расчета, для чего римская система была совершенно неприменима. Греки разделили двадцать четыре буквы своего алфавита на три класса, и, добавляя еще один символ к каждому классу, они получили символы для представления единиц, десятков и сотен. ( Жан Батист Жозеф Деламбр , Astronomie Ancienne, т. ii.)

Эта система появилась в третьем веке до нашей эры, до того, как буквы дигамма (Ϝ), коппа (Ϟ) и сампи (Ϡ) вышли из употребления. Когда строчные буквы стали отличаться от заглавных, строчные буквы стали использоваться в качестве символов для записи. Кратные тысяче числа записывались как девять цифр со штрихом перед ними: так, тысяча была ",α", две тысячи была ",β" и т. д. M (для μύριοι, как в "мириада") использовалась для умножения чисел на десять тысяч. Например, число 88 888 888 будет записано как M,ηωπη*ηωπη. ^[24]

Греческие математические рассуждения были почти полностью геометрическими (хотя часто использовались для рассуждений о негеометрических предметах, таких как теория чисел ), и поэтому греки не интересовались алгебраическими символами. Большим исключением был Диофант Александрийский , великий алгебраист. ^[25] Его «Арифметика» была одним из текстов, в которых символы использовались в уравнениях. Она не была полностью символической, но была гораздо более символической, чем предыдущие книги. Неизвестное число называлось s. ^[26] Квадрат s был ; куб был ; четвертая степень была ; и пятая степень была . ^[27] Так, например, выражение: ${\displaystyle \Delta ^{y}}$ ${\displaystyle K^{y}}$ ${\displaystyle \Delta ^{y}\Delta }$ ${\displaystyle \Delta K^{y}}$

${\displaystyle 2x^{4}+3x^{3}-4x^{2}+5x-6}$

будет написано так: ^{[ необходима ссылка ]}

СС2 С3 х5 М С4 у6

Китайская математическая нотация

Цифры 0–9 в китайской системе цифр хуама (花碼)

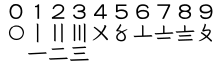
Китайцы использовали цифры, которые очень похожи на систему счета. ^[28] Цифры от одного до четырех были горизонтальными линиями. Пять была X между двумя горизонтальными линиями; она выглядела почти так же, как римская цифра десять. В настоящее время система хуама используется только для отображения цен на китайских рынках или в традиционных рукописных счетах-фактурах.

В истории китайцев были те, кто был знаком с науками арифметики, геометрии, механики, оптики, навигации и астрономии. Математика в Китае возникла независимо к 11 веку до нашей эры. ^[29] Китайцы были знакомы с астрономическими циклами, геометрическими инструментами, такими как линейка , компас и отвес , и машинами, такими как колесо и ось . Китайцы независимо разработали очень большие и отрицательные числа , десятичные дроби , десятичную систему счисления с позиционными значениями, двоичную систему , алгебру, геометрию и тригонометрию.

Счетные палочки с цифрами

Китайская математика внесла ранний вклад, включая систему разрядных значений . ^{[30] [31]} Геометрическая теорема, известная древним китайцам, была известна и применима в определенных случаях, а именно в отношении сторон . Это геометрические теоремы, которые можно продемонстрировать квазиэкспериментальным способом суперпозиции, также были им известны. В арифметике их знания, по-видимому, ограничивались искусством вычисления с помощью суаньпань и способностью выражать результаты в письменной форме. Наши знания о ранних достижениях китайцев, хотя и незначительные, более полны, чем в случае большинства их современников. Таким образом, это поучительно и служит иллюстрацией того факта, что можно знать, что нация может обладать значительным мастерством в прикладных искусствах, но наши знания о более поздней математике, на которой основаны эти искусства, могут быть скудными. Знания о китайской математике до 254 г. до н. э. несколько фрагментарны, и даже после этой даты рукописные традиции неясны. Даты, предшествующие классическому периоду, китайские ученые обычно считают предположительными, если они не подкреплены проверенными археологическими свидетельствами.

Как и в других ранних обществах, основное внимание уделялось астрономии с целью совершенствования сельскохозяйственного календаря и других практических задач, а не установлению формальных систем . Обязанности Китайского совета по математике ограничивались ежегодной подготовкой альманаха, даты и предсказания в котором он регулировал. Древние китайские математики не разработали аксиоматический подход, но добились успехов в разработке алгоритмов и алгебры. Достижения китайской алгебры достигли своего апогея в 13 веке, когда Чжу Шицзе изобрел метод четырех неизвестных.

В результате очевидных языковых и географических барьеров, а также содержания, китайская математика и математика древнего средиземноморского мира, как предполагается, развивались более или менее независимо друг от друга вплоть до того времени, когда « Девять глав о математическом искусстве» достигли своей окончательной формы, в то время как « Книга о числах и вычислениях» и «Хуайнаньцзы» примерно современны классической греческой математике. Вероятен некоторый обмен идеями по всей Азии посредством известных культурных обменов, по крайней мере, со времен Римской империи. Часто элементы математики ранних обществ соответствуют рудиментарным результатам, найденным позже в таких разделах современной математики, как геометрия или теория чисел . Например, теорема Пифагора была засвидетельствована в « Чжоуби Суаньцзине» . Также было показано, что знание треугольника Паскаля существовало в Китае за столетия до Блеза Паскаля ^[32] , сформулированное математиками, такими как полимат Шэнь Ко (1031–1095).

Состояние тригонометрии продвинулось во времена династии Сун (960–1279), когда китайские математики начали уделять больше внимания необходимости сферической тригонометрии в календарной науке и астрономических вычислениях. ^[33] Шэнь Ко использовал тригонометрические функции для решения математических задач хорд и дуг. ^[33] Сал Рестиво пишет, что работа Шэня по длинам дуг окружностей заложила основу для сферической тригонометрии, разработанной в 13 веке математиком и астрономом Го Шоуцзином (1231–1316). ^[34] Как утверждают историки Л. Гоше и Джозеф Нидхэм, Го Шоуцзин использовал сферическую тригонометрию в своих вычислениях для улучшения календарной системы и китайской астрономии . ^{[33] [35]} Математическая наука китайцев включила в себя труды и учения арабских миссионеров, обладавших знаниями сферической тригонометрии, которые прибыли в Китай в течение тринадцатого века.

Индийские и арабские цифры и обозначения

Хотя происхождение нашей нынешней системы числовых обозначений древнее, нет сомнений, что она использовалась индусами более двух тысяч лет назад. Алгебраическая нотация индийского математика Брахмагупты была синкопированной . Сложение обозначалось размещением чисел рядом, вычитание — размещением точки над вычитаемым ( числом, которое нужно вычесть), а деление — размещением делителя под делимым, аналогично нашей нотации, но без черты. Умножение, эволюция и неизвестные величины представлялись сокращениями соответствующих терминов. ^[36] Индо -арабская система счисления и правила использования ее операций, используемые сегодня во всем мире, вероятно, развивались в течение первого тысячелетия нашей эры в Индии и были переданы на Запад через исламскую математику. ^{[37] [38]}

Страница из « Алгебры » аль-Хорезми

Несмотря на свое название, арабские цифры имеют индийские корни. Причина этого неправильного названия в том, что европейцы увидели цифры, используемые в арабской книге « О индуистском искусстве счета » Мухаммеда ибн-Мусы аль-Хорезми . Аль-Хорезми написал несколько важных книг об индуистско-арабских цифрах и о методах решения уравнений. Его книга « О расчетах с помощью индуистских цифр» , написанная около 825 года, наряду с работой Аль-Кинди , сыграли важную роль в распространении индийской математики и индийских цифр на Западе. Аль-Хорезми не утверждал, что цифры арабские, но в нескольких латинских переводах тот факт, что цифры были индийского происхождения, был утерян. Слово «алгоритм» произошло от латинизации имени Аль-Хорезми — «Алгоритми», а слово «алгебра» — от названия одной из его работ — « Аль-Китаб аль-мухтасар фи хисаб аль-габр ва'ль-мукабала» ( «Краткая книга об исчислении путем завершения и уравновешивания» ).

Исламская математика развила и расширила математику, известную цивилизациям Центральной Азии , ^[39] включая добавление десятичной точки к арабским цифрам . ^{[ противоречиво ]}

Современные арабские цифровые символы, используемые во всем мире, впервые появились в исламской Северной Африке в 10 веке. Отличительный западный арабский вариант восточных арабских цифр начал появляться около 10 века в Магрибе и Аль-Андалусе (иногда называемый губарскими цифрами, хотя этот термин не всегда принимается), которые являются прямыми предками современных арабских цифр, используемых во всем мире. ^[40]

Многие греческие и арабские тексты по математике были затем переведены на латынь , что привело к дальнейшему развитию математики в средневековой Европе. В XII веке ученые отправились в Испанию и Сицилию в поисках научных арабских текстов, включая текст аль-Хорезми (переведенный на латынь Робертом Честерским ) и полный текст «Начал » Евклида (переведенный в различных версиях Аделардом Батским , Германом Каринтийским и Герардом Кремонским ). ^{[41] [42]} Одной из европейских книг, пропагандировавших использование цифр, была «Liber Abaci » Леонардо Пизанского, более известного как Фибоначчи . «Liber Abaci» больше известна по математической задаче, которую Фибоначчи написал в ней о популяции кроликов. Рост популяции в конечном итоге оказался последовательностью Фибоначчи , где член является суммой двух предыдущих членов.

Символическая сцена

Символы по популярной дате введения

Ранняя арифметика и умножение

Переход к символической алгебре, где используются только символы, впервые можно увидеть в работах Ибн аль-Банны аль-Марракуши (1256–1321) и Абу аль-Хасана ибн Али аль-Каласади (1412–1482). ^{[43] [44]} Аль-Каласади был последним крупным средневековым арабским алгебраистом , который улучшил алгебраическую нотацию, ранее использовавшуюся в Магрибе Ибн аль-Банной. ^[45] В отличие от синкопированных нотаций их предшественников, Диофанта и Брахмагупты , в которых отсутствовали символы для математических операций , ^[46] алгебраическая нотация аль-Каласади была первой, в которой использовались символы для этих функций, и, таким образом, была «первым шагом к введению алгебраической символики». Он представлял математические символы, используя буквы арабского алфавита . ^[45]

Использование знаков «плюс» и «минус» в печати в 1489 году.

В XIV веке появились новые математические концепции для исследования широкого круга проблем. ^[47] Два широко используемых арифметических символа — это сложение и вычитание, + и −. Знак плюс начал использоваться примерно с 1351 года Николем Оремом ^[48] и был опубликован в 1360 году в его работе Algorismus rationum . ^[49] Считается, что это сокращение от «et», что на латыни означает «и», во многом так же, как знак амперсанда также начинался как «et». Орем в Парижском университете и итальянец Джованни ди Казали независимо друг от друга представили графические демонстрации расстояния, пройденного телом, совершающим равномерно ускоренное движение, утверждая, что площадь под линией, изображающей постоянное ускорение, и представляет собой общее пройденное расстояние. ^[50] Знак минус был использован в 1489 году Иоганнесом Видманом в работе «Торговая арифметика» или «Бехенде и хюпсче Рехенунг ауфф аллэн Кауфманшафт» . ^[51] Видман использовал символ минус с символом плюс, чтобы обозначить дефицит и излишек соответственно. ^[52] В «Сумме арифметики, геометрии, пропорций и пропорционалита » ^[53] Лука Пачоли использовал символы для символов плюс и минус и содержал алгебру , хотя большая часть работы была написана Пьеро делла Франческа, которого он присвоил и украл. ^{[ необходима ссылка ]}

Символ радикала (√) для квадратного корня был введен Кристофом Рудольфом в начале 1500-х годов. Важный труд Михаэля Штифеля Arithmetica integra ^[54] содержал важные нововведения в математической нотации. В 1556 году Никколо Тарталья использовал скобки для группировки по приоритету. В 1557 году Роберт Рекорде опубликовал The Whetstone of Witte , в котором ввел знак равенства (=), а также знаки плюс и минус для английского читателя. В 1564 году Джероламо Кардано проанализировал азартные игры, положив начало ранним этапам теории вероятностей . В 1572 году Рафаэль Бомбелли опубликовал свою L'Algebra , в которой показал, как обращаться с мнимыми величинами , которые могли появляться в формуле Кардано для решения кубических уравнений. Книга Симона Стевина De Thiende («Искусство десятых»), опубликованная на голландском языке в 1585 году, содержала систематическую обработку десятичной записи , которая повлияла на все последующие работы по действительной системе чисел . Новая алгебра (1591) Франсуа Виета ввела современную нотацию манипуляций алгебраическими выражениями.

Джон Непер наиболее известен как изобретатель логарифмов (опубликовано в «Description of the Marvelous Canon of Logarithms ») ^[55] и сделал общепринятым использование десятичной точки в арифметике и математике. ^{[56] [57]} После Непера Эдмунд Гюнтер создал логарифмические шкалы (линии или линейки), на которых основаны логарифмические линейки , именно Уильям Отред использовал две такие шкалы, скользящие друг по другу, для выполнения прямого умножения и деления ; и ему приписывают звание изобретателя логарифмической линейки в 1622 году. В 1631 году Отред ввел знак умножения (×), свой знак пропорциональности (∷) и сокращения sin и cos для функций синуса и косинуса . ^[58] Альбер Жирар также использовал сокращения «sin», «cos» и «tan» для тригонометрических функций в своем трактате.

Рене Декарт считается отцом аналитической геометрии , моста между алгеброй и геометрией, сыгравшего решающую роль в открытии исчисления и анализа бесконечно малых . В 17 веке Декарт ввел декартовы координаты , которые позволили развить аналитическую геометрию, ввести запись уравнений в геометрию. Блез Паскаль оказывал влияние на математику на протяжении всей своей жизни. Его «Трактат об арифметическом треугольнике » 1653 года описал удобное табличное представление для биномиальных коэффициентов , теперь называемое треугольником Паскаля . Джон Уоллис ввел символ бесконечности (∞) и также использовал эту запись для бесконечно малых , например, ⁠1/∞⁠ .

Иоганн Ран ввел знак деления (÷, переосмысленный вариант обелуса ) и, следовательно, знак в 1659 году. Уильям Джонс использовал π в Synopsis palmariorum mathesios ^[59] в 1706 году, потому что это начальная буква греческого слова Perimetron (περιμετρον), что означает периметр на греческом языке. Такое использование было популяризировано в 1737 году Эйлером. В 1734 году Пьер Бугер использовал двойную горизонтальную черту под знаком неравенства . ^[60]

Обозначения производных: Лейбниц и Ньютон

Производные обозначения

Изучение линейной алгебры возникло из изучения определителей , которые использовались для решения систем линейных уравнений . Исчисление имело две основные системы обозначений, каждая из которых была создана одним из создателей: система, разработанная Исааком Ньютоном , и система обозначений, разработанная Готфридом Лейбницем . Система обозначений Лейбница используется сегодня чаще всего. Система обозначений Ньютона представляла собой просто точку или тире, помещенные над функцией. Например, производная функции x будет записана как . Вторая производная x будет записана как . В современном использовании эта запись обычно обозначает производные физических величин по времени и часто используется в науке механике . Лейбниц, с другой стороны, использовал букву d в качестве префикса для обозначения дифференциации и ввел обозначение, представляющее производные, как если бы они были особым типом дроби. Например, производная функции x по переменной t в системе обозначений Лейбница будет записана как . Эта запись делает явной переменную, по которой берется производная функции. Лейбниц также создал символ интеграла ( ∫ ). Например: . При нахождении площадей под кривыми интегрирование часто иллюстрируется делением площади на бесконечное количество высоких тонких прямоугольников, площади которых складываются. Таким образом, символ интеграла представляет собой вытянутую букву S , представляющую латинское слово summa , означающее «сумма». ${\displaystyle {\dot {x}}}$ ${\displaystyle {\ddot {x}}}$ ${\displaystyle {dx \over dt}}$ ${\displaystyle \int _{-N}^{N}f(x)\,dx}$

Операторы и функции высокого деления

Буквы алфавита в это время должны были использоваться как символы количества ; и хотя существовало много разнообразия в отношении выбора букв, в последующей истории должно было быть несколько общепризнанных правил . ^[23] Таким образом, в истории уравнений первые буквы алфавита были условно известны как коэффициенты , последние буквы - неизвестные члены ( incerti ordinis ). В алгебраической геометрии , опять же, должно было соблюдаться похожее правило, последние буквы алфавита там обозначали переменную или текущие координаты . Некоторые буквы, такие как , и т. д ., были по всеобщему согласию приняты в качестве символов часто встречающихся чисел 3,14159 ... и 2,7182818 .... , а других использований следовало избегать, насколько это возможно. ^[23] Буквы также должны были использоваться как символы операции, а вместе с ними и другие ранее упомянутые произвольные символы операции. Буквы , удлиненные, должны были быть присвоены в качестве операционных символов в дифференциальном исчислении и интегральном исчислении , а Σ — в исчислении разностей . ^[23] В функциональной нотации буква, как символ операции, сочетается с другой, которая рассматривается как символ количества . ^[23] ${\displaystyle \pi }$ ${\displaystyle e}$ ${\displaystyle d}$ ${\displaystyle S}$ ${\displaystyle \Delta }$

Таким образом, обозначает математический результат выполнения операции над субъектом . Если бы над этим результатом была повторена та же операция, новый результат был бы выражен посредством , или более кратко посредством , и так далее. Сама величина , рассматриваемая как результат той же операции над некоторой другой функцией; надлежащим символом для которой является, по аналогии, . Таким образом, и являются символами обратных операций , причем первая отменяет эффект последней на субъект . и аналогичным образом называются обратными функциями . ${\displaystyle f(x)}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle f[f(x)]}$ ${\displaystyle f^{2}(x)}$ ${\displaystyle x}$ ${\displaystyle f}$ ${\displaystyle f^{-1}(x)}$ ${\displaystyle f}$ ${\displaystyle f^{-1}}$ ${\displaystyle x}$ ${\displaystyle f(x)}$ ${\displaystyle f^{-1}(x)}$

Начиная с 1718 года Томас Твинен использовал косую черту ( солидус ), выведя ее из более ранней арабской горизонтальной дробной черты . Пьер-Симон, маркиз де Лаплас разработал широко используемый дифференциальный оператор Лапласа (например ). В 1750 году Габриэль Крамер разработал « Правило Крамера » для решения линейных систем . ${\displaystyle \Delta f(p)}$

Обозначения Эйлера и простые обозначения

Подпись Леонарда Эйлера

Леонард Эйлер был одним из самых плодовитых математиков в истории, а также плодовитым изобретателем канонической нотации. Его вклад включает использование e для представления основания натуральных логарифмов . Точно неизвестно, почему был выбран этот вариант, но, вероятно, это произошло потому, что четыре буквы алфавита уже широко использовались для представления переменных и других констант. Эйлер использовал для последовательного представления числа π . Использование было предложено Уильямом Джонсом , который использовал его в качестве сокращения для периметра . Эйлер использовал для представления квадратного корня из отрицательной единицы ( ), хотя ранее он использовал его как бесконечное число. Сегодня для обозначения бесконечности используется символ, созданный Джоном Уоллисом , , например . Для суммирования Эйлер использовал увеличенную форму вертикальной заглавной греческой буквы сигма (Σ), известную как запись с заглавной сигмой . Она определяется как: ${\displaystyle e}$ ${\displaystyle \pi }$ ${\displaystyle \pi }$ ${\displaystyle i}$ ${\displaystyle {\sqrt {-1}}}$ ${\displaystyle \infty }$ ${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}}$

${\displaystyle \sum _{i=m}^{n}a_{i}=a_{m}+a_{m+1}+a_{m+2}+\cdots +a_{n-1}+a_{n}.}$

где i представляет собой индекс суммирования ; a _i — индексированная переменная, представляющая каждый последующий член в ряду; m — нижняя граница суммирования , а n — верхняя граница суммирования . «i = m» под символом суммирования означает, что индекс i изначально равен m . Индекс i увеличивается на 1 для каждого последующего члена, останавливаясь, когда i = n .

Для функций Эйлер использовал обозначение для представления функции от . ${\displaystyle f(x)}$ ${\displaystyle x}$

Математик Уильям Эмерсон ^[61] разработал знак пропорциональности (∝). Пропорциональность — это отношение одной величины к другой, и этот знак используется для указания того, что отношение между двумя переменными является постоянным. ^{[62] [63]} Намного позже в абстрактных выражениях значения различных пропорциональных явлений обозначение частей на единицу стало полезным как набор псевдоединиц для описания малых значений различных безразмерных величин . Маркиз де Кондорсе в 1768 году выдвинул знак частного дифференциала , известный как фигурная d или дельта Якоби . Символ-штрих для производных также был создан Жозефом-Луи Лагранжем .

Однако, по нашему мнению, истины такого рода следует черпать из понятий, а не из обозначений.

—  Карл Фридрих Гаусс, пишущий о доказательстве теоремы Вильсона ^[64]

Обозначения Гаусса, Гамильтона и матрицы

На рубеже 19-го века Карл Фридрих Гаусс разработал знак тождества для отношения конгруэнтности и, в квадратичном законе взаимности , целую часть . Гаусс внес вклад в функции комплексных переменных в геометрии и в сходимость рядов . Он дал удовлетворительные доказательства основной теоремы алгебры и квадратичного закона взаимности . Гаусс разработал теорию решения линейных систем с использованием метода исключения Гаусса , что изначально было указано как достижение в геодезии . ^[65] Он также разработал знак произведения .

После 1800-х годов Кристиан Крамп продвигал факториальную нотацию во время своих исследований обобщенной факториальной функции, которая применялась к нецелым числам. ^[66] Жозеф Диас Жергонн ввел знаки включения множеств (⊆, ⊇), позже переработанные Эрнстом Шредером . Петер Густав Лежен Дирихле разработал L -функции Дирихле, чтобы дать доказательство теоремы Дирихле об арифметических прогрессиях и начал аналитическую теорию чисел . В 1829 году Карл Густав Якоб Якоби опубликовал Fundamenta nova theoriae functionum ellipticarum со своими эллиптическими тета-функциями .

Матричную нотацию более полно развил Артур Кэли в своих трех работах по темам, которые были предложены при чтении Mécanique analytique ^[67] Лагранжа и некоторых работ Лапласа. Кэли определил умножение матриц и обратные матрицы . Кэли использовал одну букву для обозначения матрицы ^[68] , таким образом, рассматривая матрицу как агрегатный объект. Он также осознал связь между матрицами и детерминантами ^[69] и написал: « Можно было бы сказать много вещей об этой теории матриц, которые, как мне кажется, должны предшествовать теории детерминантов ». ^[70]

Уильям Роуэн Гамильтон ввел символ набла ( или, позже названный del , ∇) для векторных дифференциалов . ^{[71] [72]} Ранее Гамильтон использовал его в качестве знака оператора общего назначения . ^[73] , и используются для оператора Гамильтона в квантовой механике , а ℋ для функции Гамильтона в классической гамильтоновой механике . ${\displaystyle \nabla }$ ${\displaystyle {\hat {H}}}$ ${\displaystyle H}$ ${\displaystyle {\check {H}}}$

В математике Гамильтон, пожалуй, наиболее известен как изобретатель кватернионной записи и бикватернионов .

Нотации Максвелла, Клиффорда и Риччи

Джеймс Клерк Максвелл

---

Самым выдающимся достижением Максвелла была формулировка системы уравнений , которая объединила ранее не связанные между собой наблюдения, эксперименты и уравнения электричества , магнетизма и оптики в последовательную теорию. ^[74]

В 1864 году Джеймс Клерк Максвелл свел все имевшиеся на тот момент знания об электромагнетизме к связанному набору дифференциальных уравнений с 20 уравнениями с 20 переменными, содержащемуся в «Динамической теории электромагнитного поля» . ^[75] (См. уравнения Максвелла .) Метод расчета, который необходимо использовать, был дан Лагранжем, а затем развит, с некоторыми изменениями, уравнениями Гамильтона . Обычно его называют принципом Гамильтона ; когда используются уравнения в исходной форме, они известны как уравнения Лагранжа . В 1871 году Ричард Дедекинд назвал множество действительных или комплексных чисел, которое замкнуто относительно четырех арифметических операций, полем . В 1873 году Максвелл представил «Трактат об электричестве и магнетизме» .

В 1878 году Уильям Кингдон Клиффорд опубликовал свои «Элементы динамики» . ^[76] Клиффорд разработал расщепленные бикватернионы (например, ), которые он назвал алгебраическими двигателями . Клиффорд устранил необходимость изучения кватернионов, отделив скалярное произведение и перекрестное произведение двух векторов от полной записи кватернионов. ${\displaystyle q=w+xi+yj+zk}$

Обычные векторные обозначения используются при работе с векторами, которые являются пространственными или более абстрактными элементами векторных пространств , в то время как угловые обозначения (или фазовые обозначения) используются в электронике .

Теория эфирного атома лорда Кельвина ( 1860-е годы) привела Питера Гатри Тейта в 1885 году к публикации топологической таблицы узлов с числом пересечений до десяти, известной как гипотезы Тейта . Тензорное исчисление было разработано Грегорио Риччи-Курбастро между 1887 и 1896 годами, представлено в 1892 году под названием «абсолютное дифференциальное исчисление » ^[77], а современное использование термина «тензор» было сформулировано Вольдемаром Фойгтом в 1898 году . ^[78] В 1895 году Анри Пуанкаре опубликовал «Анализ Situs» . ^[79] В 1897 году Чарльз Протеус Штейнмец опубликовал «Теорию и расчет явлений переменного тока» при содействии Эрнста Й. Берга. ^[80]

От формульной математики к тензорам

В 1895 году Джузеппе Пеано выпустил свой Formulario mathematico [ ^81] , попытку переварить математику в сжатый текст на основе специальных символов. Он дал определение векторного пространства и линейного отображения . Он также ввел знак пересечения , знак объединения , знак принадлежности (является элементом) и квантификатор существования (существует). Пеано передал свою работу Бертрану Расселу в 1900 году на Парижской конференции; она так впечатлила Рассела, что Рассел тоже был увлечен стремлением изложить математику более кратко. Результатом стала работа Principia Mathematica, написанная совместно с Альфредом Норт Уайтхедом . Этот трактат знаменует собой водораздел в современной литературе, где символ стал доминирующим. Formulario Mathematico Пеано , хотя и менее популярная, чем работа Рассела, выдержала пять изданий. Пятое появилось в 1908 году и включало 4200 формул и теорем.

Риччи-Курбастро и Туллио Леви-Чивита популяризировали обозначение тензорного индекса около 1900 года. ^[82]

Математическая логика и абстракция

Георг Кантор , изобретатель теории множеств , ввел числа Алеф , названные так потому, что они используют символ алеф (א) с натуральными индексами для мощности в бесконечных множествах . Для ординалов он использовал греческую букву ω ( омега ). Эта нотация используется и сегодня в порядковой нотации конечной последовательности символов из конечного алфавита, который называет порядковое число в соответствии с некоторой схемой, которая придает смысл языку.

После рубежа 20-го века Джозайя Уиллард Гиббс ввел в физической химии среднюю точку для скалярного произведения и знак умножения для перекрестных произведений . Он также ввел обозначения для скалярных и векторных произведений, которые были введены в векторном анализе . Бертран Рассел вскоре после этого ввел логическую дизъюнкцию ( ИЛИ ) в 1906 году . Герхард Ковалевски и Катберт Эдмунд Куллис ^{[83] [84] [85]} последовательно ввели матричную нотацию, скобочную матричную нотацию и блочную матричную нотацию соответственно.

Альберт Эйнштейн в 1921 году

Альберт Эйнштейн в 1916 году ввел обозначение Эйнштейна , которое суммировало по набору индексированных членов в формуле, тем самым обеспечивая краткость обозначений. Например, индексы ранжируются по набору {1, 2, 3 }:

${\displaystyle y=\sum _{i=1}^{3}c_{i}x^{i}=c_{1}x^{1}+c_{2}x^{2}+c_{3}x^{3}}$

сводится по соглашению к:

${\displaystyle y=c_{i}x^{i}\,.}$

Верхние индексы не являются показателями степени , а являются индексами координат, коэффициентов или базисных векторов .

Арнольд Зоммерфельд создал контурный интеграл в 1917 году. Также в 1917 году Дмитрий Мириманов предложил аксиому регулярности . В 1919 году Теодор Калуца ​​решил уравнения общей теории относительности, используя пять измерений , в результате чего появились электромагнитные уравнения. ^[86] Это было опубликовано в 1921 году в «Zum Unitätsproblem der Physik». ^[87] В 1922 году Авраам Френкель и Торальф Скулем независимо друг от друга предложили заменить схему аксиом спецификации на схему аксиом замены . Также в 1922 году была разработана теория множеств Цермело–Френкеля . В 1923 году Штейнмец опубликовал «Четыре лекции по теории относительности и пространству». Около 1924 года Ян Арнольдус Схоутен разработал современную нотацию и формализм для структуры исчисления Риччи во время приложений абсолютного дифференциального исчисления к общей теории относительности и дифференциальной геометрии в начале двадцатого века. Исчисление Риччи представляет собой правила индексной нотации и манипуляции для тензоров и тензорных полей . ^{[88] [89] [90] [91]} В 1925 году Энрико Ферми описал систему, состоящую из множества идентичных частиц, которые подчиняются принципу исключения Паули , после чего разработал уравнение диффузии ( уравнение возраста Ферми ). В 1926 году Оскар Клейн разработал теорию Калуцы–Клейна . В 1928 году Эмиль Артин абстрагировал теорию колец с помощью артиновых колец . В 1933 году Андрей Колмогоров вводит аксиомы Колмогорова . В 1937 году Бруно де Финетти вывел концепцию « операционального субъективизма » .

Математическая символика

Математическая абстракция началась как процесс извлечения базовой сущности математической концепции, ^{[92] [93]} устранения любой зависимости от объектов реального мира, с которыми она могла быть изначально связана, ^[94] и обобщения ее таким образом, чтобы она имела более широкие приложения или совпадала с другими абстрактными описаниями эквивалентных явлений . Две абстрактные области современной математики — это теория категорий и теория моделей . Бертран Рассел ^[95] сказал: « Обычный язык совершенно не подходит для выражения того, что физика действительно утверждает, поскольку слова повседневной жизни недостаточно абстрактны. Только математика и математическая логика могут сказать так мало, как физик имеет в виду сказать ». Хотя можно заменить математикой объекты реального мира и блуждать по уравнениям и построить концептуальную структуру, которая не имеет никакого отношения к реальности. ^[96]

Некоторые из введенных в то время математических логических обозначений включали набор символов, используемых в булевой алгебре . Он был создан Джорджем Булем в 1854 году. Сам Буль не рассматривал логику как раздел математики, но она так или иначе стала охватываться. Символы, встречающиеся в булевой алгебре, включают (И), (ИЛИ) и ( не ). С помощью этих символов и букв для представления различных значений истинности можно делать логические утверждения, такие как «( a истинно ИЛИ a не истинно ) истинно», что означает, что истинно, что a либо истинно, либо не истинно (т. е. ложно). Булева алгебра сама по себе имеет множество практических применений, но она также стала началом того, что будет большим набором символов для использования в логике. Большинство этих символов можно найти в исчислении высказываний , формальной системе, описываемой как . — это множество элементов, таких как a в примере с булевой алгеброй выше. — это множество, которое содержит подмножества, содержащие операции, такие как или . содержит правила вывода , которые являются правилами, диктующими, как логически могут быть сделаны выводы, и содержит аксиомы . Логика предикатов, первоначально называвшаяся исчислением предикатов , расширяет пропозициональную логику введением переменных , обычно обозначаемых как x , y , z или другими строчными буквами, и предложений, содержащих переменные, называемых предикатами . Они обычно обозначаются заглавной буквой, за которой следует список переменных, например P( x ) или Q( y , z ). Логика предикатов использует специальные символы для квантификаторов : ∃ для «существует» и ∀ для «для всех». ${\displaystyle \land }$ ${\displaystyle \lor }$ ${\displaystyle \lnot }$ ${\displaystyle a\lor \lnot a=1}$ ${\displaystyle {\mathcal {L}}={\mathcal {L}}\ (\mathrm {A} ,\ \Omega ,\ \mathrm {Z} ,\ \mathrm {I} )}$ ${\displaystyle \mathrm {A} }$ ${\displaystyle \Omega }$ ${\displaystyle \lor }$ ${\displaystyle \land }$ ${\displaystyle \mathrm {Z} }$ ${\displaystyle \mathrm {I} }$

Нотация неполноты Гёделя

Каждому ω-согласованному рекурсивному классу κ формул соответствуют рекурсивные знаки класса r , такие, что ни v Gen r, ни Neg ( v Gen r ) не принадлежат Flg (κ) (где v — свободная переменная r ) .

—  Курт Гёдель ^[97]

Доказывая свои теоремы о неполноте , Курт Гёдель создал альтернативу символам, обычно используемым в логике. Он использовал числа Гёделя , которые были числами, представляющими операции с заданными числами и переменными с простыми числами больше 10. С помощью чисел Гёделя логические утверждения можно разбить на числовую последовательность. Затем Гёдель сделал еще один шаг вперед, взяв n простых чисел и возведя их в степень чисел в последовательности. Затем эти числа были перемножены, чтобы получить конечный продукт, придав каждому логическому утверждению свой собственный номер. ^[98]

Например, возьмем утверждение "Существует число x, такое что оно не есть y ". Используя символы исчисления высказываний, это будет выглядеть так:

${\displaystyle (\exists x)(x=\lnot y)}$.

Если заменить символы числами Гёделя, то получится:

${\displaystyle \{8,4,11,9,8,11,5,1,13,9\}}$.

Имеется десять чисел, поэтому найдены десять простых чисел:

${\displaystyle \{2,3,5,7,11,13,17,19,23,29\}}$.

Затем числа Гёделя возводятся в степени соответствующих простых чисел и умножаются, что дает:

${\displaystyle 2^{8}\times 3^{4}\times 5^{11}\times 7^{9}\times 11^{8}\times 13^{11}\times 17^{5}\times 19^{1}\times 23^{13}\times 29^{9}}$.

Полученное число приблизительно равно . ${\displaystyle 3.096262735\times 10^{78}}$

Современная нотация и темы

Нотная запись начала 20-го века

Абстрагирование обозначений — это непрерывный процесс, и историческое развитие многих математических тем демонстрирует прогресс от конкретного к абстрактному. Различные обозначения множеств будут разработаны для фундаментальных наборов объектов . Около 1924 года Дэвид Гильберт и Ричард Курант опубликовали « Методы математической физики. Уравнения с частными производными ». ^[99] В 1926 году Оскар Клейн и Уолтер Гордон предложили уравнение Клейна–Гордона для описания релятивистских частиц:

${\displaystyle {\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\psi -\nabla ^{2}\psi +{\frac {m^{2}c^{2}}{\hbar ^{2}}}\psi =0.}$

Первая формулировка квантовой теории, описывающей взаимодействие излучения и материи, принадлежит Полю Адриену Морису Дираку , который в 1920 году впервые смог вычислить коэффициент спонтанного излучения атома . [ ^100] В 1928 году Дирак сформулировал релятивистское уравнение Дирака для объяснения поведения релятивистски движущегося электрона . Уравнение Дирака в форме, первоначально предложенной Дираком, выглядит следующим образом:

${\displaystyle \left(\beta mc^{2}+\sum _{k=1}^{3}\alpha _{k}p_{k}\,c\right)\psi (\mathbf {x} ,t)=i\hbar {\frac {\partial \psi (\mathbf {x} ,t)}{\partial t}}}$

где, ψ = ψ( x , t ) — волновая функция электрона , x и t — пространственные и временные координаты, m — масса покоя электрона, p — импульс , понимаемый как оператор импульса в теории Шредингера , c — скорость света , а ħ = h /2 π — приведенная постоянная Планка . Дирак описал квантификацию электромагнитного поля как ансамбля гармонических осцилляторов , введя концепцию операторов рождения и уничтожения частиц. В последующие годы, с вкладом Вольфганга Паули , Юджина Вигнера , Паскуаля Йордана и Вернера Гейзенберга , а также с элегантной формулировкой квантовой электродинамики, предложенной Энрико Ферми , ^[101] физики пришли к убеждению, что, в принципе, можно выполнить любое вычисление для любого физического процесса с участием фотонов и заряженных частиц.

В 1931 году Александру Прока разработал уравнение Прока ( уравнение Эйлера–Лагранжа ) для векторной мезонной теории ядерных сил и релятивистских квантовых уравнений поля . Джон Арчибальд Уилер в 1937 году разрабатывает S-матрицу . Исследования Феликса Блоха с Арнольдом Нордсиком [ ^102] и Виктором Вайскопфом [ ^103] в 1937 и 1939 годах показали, что такие вычисления надежны только в первом порядке теории возмущений , проблема, на которую уже указывал Роберт Оппенгеймер ^[104] . В более высоких порядках в ряду появлялись бесконечности, что делало такие вычисления бессмысленными и вызывало серьезные сомнения во внутренней согласованности самой теории. Поскольку в то время не было известно решения этой проблемы, казалось, что между специальной теорией относительности и квантовой механикой существует фундаментальная несовместимость .

В 1930-х годах Эдмунд Ландау создал заглавную букву Z с двойным ударом для множеств целых чисел . Николя Бурбаки создал заглавную букву Q с двойным ударом для множеств рациональных чисел. В 1935 году Герхард Генцен создал универсальные квантификаторы . Андре Вайль и Николя Бурбаки разработали знак пустого множества в 1939 году. В том же году Натан Якобсон придумал заглавную букву C с двойным ударом для множеств комплексных чисел.

Около 1930-х годов нотация Фойгта (названная так в честь работы Фойгта 1898 года) была разработана для полилинейной алгебры как способ представления симметричного тензора путем понижения его порядка. Нотация Шёнфлиса стала одним из двух соглашений, используемых для описания точечных групп (другое — нотация Германа–Могена ). Также в это время нотация Ван дер Вардена ^{[105] [106]} стала популярной для использования двухкомпонентных спиноров ( спиноров Вейля ) в четырех измерениях пространства-времени. Аренд Гейтинг ввел алгебру Гейтинга и арифметику Гейтинга .

Стрелка, например, →, была разработана для обозначения функций в 1936 году Эйстейном Оре для обозначения изображений определенных элементов и для обозначения связей Галуа . Позднее, в 1940 году, она приняла свою нынешнюю форму, например, f: X → Y , благодаря работе Витольда Гуревича . Вернер Гейзенберг в 1941 году предложил теорию S-матрицы взаимодействий частиц.

Поль Дирак , изображенный здесь, внес фундаментальный вклад в раннее развитие квантовой механики и квантовой электродинамики .

Обозначение Бра–кет ( обозначение Дирака ) — это стандартное обозначение для описания квантовых состояний , состоящее из угловых скобок и вертикальных черт . Его также можно использовать для обозначения абстрактных векторов и линейных функционалов . Оно так называется, потому что скалярное произведение (или скалярное произведение в комплексном векторном пространстве) двух состояний обозначается как ⟨bra|ket⟩:. Обозначение было введено в 1939 году Полем Дираком ^[107], хотя у обозначения есть предшественники в виде использования Грассманом обозначения [ φ | ψ ] для его скалярных произведений почти 100 лет назад. ^[108] ${\displaystyle \langle \phi |\psi \rangle }$

Обозначение Бра-кет широко распространено в квантовой механике : почти каждое явление, которое объясняется с помощью квантовой механики, включая большую часть современной физики , обычно объясняется с помощью обозначения Бра-кет. Обозначение устанавливает закодированную абстрактную независимость представления, производя универсальное конкретное представление (например, x или p или базу собственных функций ) без особых хлопот или чрезмерной зависимости от природы вовлеченных линейных пространств. Выражение перекрытия ⟨ φ | ψ ⟩ обычно интерпретируется как амплитуда вероятности коллапса состояния ψ в состояние ϕ . Обозначение косой черты Фейнмана ( обозначение косой черты Дирака [ 109 ] ) ^было разработано Ричардом Фейнманом для изучения полей Дирака в квантовой теории поля .

Джеффри Чу , наряду с другими, продвигал матричную нотацию для сильного взаимодействия в физике элементарных частиц и связанный с ней принцип бутстрапа в 1960 году. В 1960-х годах была разработана нотация set-builder для описания множества путем указания свойств, которым должны удовлетворять его члены. Также в 1960-х годах тензоры абстрагируются в рамках теории категорий с помощью концепции моноидальной категории . Позже многоиндексная нотация устраняет общепринятые понятия, используемые в многомерном исчислении , уравнениях с частными производными и теории распределений , абстрагируя концепцию целочисленного индекса до упорядоченного кортежа индексов.

Современная математическая нотация

В современной математике специальной теории относительности , электромагнетизма и волновой теории оператор Даламбера ( ) является оператором Лапласа пространства Минковского . Символ Леви-Чивиты , также известный как символ перестановки , используется в тензорном исчислении . ${\displaystyle \scriptstyle \Box }$

Диаграммы Фейнмана используются в физике элементарных частиц, эквивалентно операторному подходу Син-Итиро Томонаги и Джулиана Швингера . Система обозначений орбифолда , изобретенная Уильямом Терстоном , была разработана для представления типов групп симметрии в двумерных пространствах постоянной кривизны.

Формализм тетрады ( тетрадная индексная нотация ) будет введен как подход к общей теории относительности , который заменяет выбор координатного базиса менее ограничительным выбором локального базиса для касательного расслоения (локально определенного набора из четырех линейно независимых векторных полей , называемых тетрадой ) . ^[110]

В 1990-х годах Роджер Пенроуз предложил графическую нотацию Пенроуза ( нотацию тензорной диаграммы ) как, как правило, рукописное визуальное изображение полилинейных функций или тензоров . ^[111] Пенроуз также ввел абстрактную индексную нотацию . Он использовал суммирование Эйнштейна для того, чтобы компенсировать неудобства в описании сокращений и ковариантного дифференцирования в современной абстрактной тензорной нотации, сохраняя при этом явную ковариантность задействованных выражений. ^{[ необходима ссылка ]}

Джон Х. Конвей, плодовитый математик в области нотации.

Джон Конвей развил различные обозначения, включая обозначение цепочечных стрелок Конвея , обозначение теории узлов Конвея и обозначение многогранника Конвея . Система обозначений Коксетера классифицирует группы симметрии, описывая углы между с фундаментальными отражениями группы Коксетера . Она использует обозначение в скобках с модификаторами для указания определенных подгрупп. Обозначение названо в честь HSM Coxeter , а Норман Джонсон дал ему более полное определение.

Комбинаторная нотация LCF , разработанная Джошуа Ледербергом и расширенная Гарольдом Скоттом Макдональдом Коксетером и Робертом Фрухтом , была разработана для представления кубических графов , которые являются гамильтоновыми . ^{[112] [113]} Нотация цикла — это соглашение для записи перестановки в терминах ее составляющих циклов . ^[114] Это также называется круговой нотацией , а перестановка называется циклической или круговой перестановкой. ^[115]

Компьютеры и нотация разметки

В 1931 году IBM выпускает IBM 601 Multiplying Punch ; это электромеханическая машина, которая могла считывать два числа длиной до 8 цифр с карты и пробивать их результат на той же карте. ^[116] В 1934 году Уоллес Экерт использовал оснащенный IBM 601 Multiplying Punch для автоматизации интегрирования дифференциальных уравнений. ^[117]

В 1962 году Кеннет Э. Айверсон разработал нотацию интегральной части, которая стала известна как нотация Айверсона, которая развилась в APL . ^[118] В 1970-х годах в компьютерной архитектуре была разработана нотация кавычек для представления числовой системы рациональных чисел . Также в этом десятилетии нотация Z (как и язык APL , задолго до нее) использует много не- ASCII символов, спецификация включает предложения по отображению символов нотации Z в ASCII и в LaTeX . В настоящее время существуют различные математические функции C (Math.h) и числовые библиотеки. Это библиотеки, используемые при разработке программного обеспечения для выполнения числовых вычислений. Эти вычисления могут быть обработаны с помощью символьных исполнений ; анализ программы для определения того, какие входные данные заставляют каждую часть программы выполняться. Mathematica и SymPy являются примерами вычислительных программ, основанных на символьной математике .

Ссылки и цитаты

Общий

• Флориан Каджори (1929) История математических обозначений , 2 тома. Переиздание Дувра в 1 томе, 1993. ISBN  0-486-67766-4 .

Цитаты

1. Флориан Каджори . История математических обозначений: два тома в одном. Cosimo, Inc., 1 декабря 2011 г.
2. Словарь науки, литературы и искусства, том 2. Под редакцией Уильяма Томаса Бранде , Джорджа Уильяма Кокса . Стр. 683
3. "Notation – from Wolfram MathWorld". Mathworld.wolfram.com . Получено 24 июня 2014 г. .
4. Диофант Александрийский: исследование по истории греческой алгебры. Сэр Томас Литтл Хит. Стр. 77.
5. Математика: ее сила и полезность. Карл Дж. Смит. Стр. 86.
6. Коммерческая революция и начало западной математики в эпоху Возрождения во Флоренции, 1300–1500. Уоррен Ван Эгмонд. 1976. Страница 233.
7. Соломон Гандз . «Источники алгебры аль-Хорезми»
8. Encyclopaedia Americana. Томас Гамалиел Брэдфорд. Стр. 314
9. Математический экскурс, расширенное издание: расширенное издание Webassign Ричарда Н. Ауфмана, Джоанн Локвуд, Ричарда Д. Нейшна, Дэниела К. Клега. Стр. 186
10. "Математика в Египте и Месопотамии" (PDF) . Архивировано из оригинала (PDF) 28 декабря 2022 года . Получено 25 июля 2013 года .
11. Бойер, CB История математики , 2-е изд. обр. Ута К. Мерцбах . Нью-Йорк: Wiley, ISBN 1989 г. 0-471-09763-2 (изд. Pbk 1991 г. ISBN 0-471-54397-7 ). «Месопотамия» с. 25.  
12. Дункан Дж. Мелвилл (2003). Хронология третьего тысячелетия, Математика третьего тысячелетия . Университет Св. Лаврентия .
13. Аабо, Асгер (1998). Эпизоды из ранней истории математики . Нью-Йорк: Random House. С. 30–31.
14. То есть, . ${\displaystyle a^{2}+b^{2}=c^{2}}$
15. Хит (1931). «Руководство по греческой математике». Nature . 128 (3235): 5. Bibcode : 1931Natur.128..739T. doi : 10.1038/128739a0. S2CID  3994109.
16. Сэр Томас Л. Хит, «Руководство по греческой математике» , Дувр, 1963, стр. 1: «В случае с математикой наиболее важно знать греческий вклад, поскольку именно греки сделали математику наукой».
17. Новая энциклопедия; или, Универсальный словарь искусств и наук. Encyclopaedia Perthensi. Стр. 49
18. Калингер, Рональд (1999). Контекстуальная история математики . Prentice-Hall. стр. 150. ISBN 0-02-318285-7. Вскоре после Евклида, составителя окончательного учебника, появился Архимед из Сиракуз (ок. 287–212 гг. до н. э.), самый оригинальный и глубокий математик древности.
19. "Архимед Сиракузский". Архив истории математики MacTutor. Январь 1999 г. Получено 9 июня 2008 г.
20. O'Connor, JJ; Robertson, EF (февраль 1996). "История исчисления". Университет Сент-Эндрюс . Архивировано из оригинала 15 июля 2007 года . Получено 7 августа 2007 года .
21. "Proclus' Summary". Gap.dcs.st-and.ac.uk. Архивировано из оригинала 23 сентября 2015 года . Получено 24 июня 2014 года .
22. Математика и измерения Освальда Эштона Вентворта Дилка. Стр. 14
23. Словарь науки, литературы и искусства, под ред. В. Т. Бранде. Стр. 683
24. Бойер, Карл Б. История математики , 2-е издание, John Wiley & Sons, Inc., 1991.
25. Диофантовы уравнения. Представлено: Аароном Зерхузеном, Крисом Рэйксом и Шастой Мис. МА 330-002. Доктор Карл Эберхарт. 16 февраля 1999 г.
26. История греческой математики: от Аристарха до Диофанта. Сэр Томас Литтл Хит. Стр. 456
27. История греческой математики: от Аристарха до Диофанта. Сэр Томас Литтл Хит. Стр. 458
28. The American Mathematical Monthly, том 16. стр. 131
29. "Обзор китайской математики". Groups.dcs.st-and.ac.uk . Получено 24 июня 2014 г. .
30. Джордж Гевергезе Джозеф, «Хребет павлина: неевропейские корни математики» , Penguin Books, Лондон, 1991, стр. 140—148
31. Жорж Ифра, Universalgeschichte der Zahlen , Кампус, Франкфурт/Нью-Йорк, 1986, стр. 428–437.
32. «Фрэнк Дж. Суэтц и ТИ Као: был ли Пифагор китайцем?». Psupress.psu.edu . Получено 24 июня 2014 г.
33. Нидхэм, Джозеф (1986). Наука и цивилизация в Китае: Том 3, Математика и науки о небесах и земле. Тайбэй: Caves Books, Ltd.
34. Сал Рестиво
35. Марсель Гоше , 151.
36. Boyer, CB История математики, 2-е изд., перераб. Uta C. Merzbach. Нью-Йорк: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7 ). "Китай и Индия" стр. 221. (ср., "он был первым, кто дал общее решение линейного диофантова уравнения ax + by = c, где a, b и c — целые числа. [...] Большой заслугой Брахмагупты является то, что он дал все целые решения линейного диофантова уравнения, тогда как сам Диофант удовлетворился тем, что дал одно частное решение неопределенного уравнения. Поскольку Брахмагупта использовал некоторые из тех же примеров, что и Диофант, мы снова видим вероятность греческого влияния в Индии — или возможность того, что они оба использовали общий источник, возможно, из Вавилонии. Интересно также отметить, что алгебра Брахмагупты, как и алгебра Диофанта, была синкопированной. Сложение обозначалось сопоставлением, вычитание — постановкой точки над вычитаемым, а деление — постановкой делителя под делимым, как в нашей дробной записи, но без черты. Операции умножения и эволюции (взятие корни), а также неизвестные величины были представлены сокращениями соответствующих слов.")  
37. Роберт Каплан, «Ничто, что есть: естественная история нуля», Аллен Лейн/The Penguin Press, Лондон, 1999
38. ""Гениальный метод выражения всех возможных чисел с помощью набора из десяти символов (каждый символ имеет разрядное значение и абсолютное значение) появился в Индии. Идея кажется настолько простой в наши дни, что ее значимость и глубокая важность больше не ценятся. Ее простота заключается в том, как она облегчила вычисления и вывела арифметику на первое место среди полезных изобретений. Важность этого изобретения легче оценить, если учесть, что оно было за пределами двух величайших людей античности, Архимеда и Аполлония." – Пьер-Симон Лаплас". History.mcs.st-and.ac.uk . Получено 24 июня 2014 г.
39. А. П. Юшкевич , "Geschichte der Mathematik im Mittelalter", Тойбнер, Лейпциг, 1964.
40. Куницш, Пол (2003), «Пересмотр передачи индийско-арабских цифр», в JP Hogendijk; AI Sabra (ред.), Предприятие науки в исламе: новые перспективы , MIT Press, стр. 3–22 (12–13), ISBN 978-0-262-19482-2
41. Мария-Тереза ​​д'Алверни , «Переводы и переводчики», стр. 421–462 в книге Роберта Л. Бенсона и Джайлза Констебля « Возрождение и обновление в двенадцатом веке » (Кембридж: Издательство Гарвардского университета, 1982).
42. Гай Божуан, «Трансформация квадривиума», стр. 463–487 в книге Роберта Л. Бенсона и Джайлза Констебля « Возрождение и обновление в двенадцатом веке » (Кембридж: Издательство Гарвардского университета, 1982).
43. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «аль-Марракуши ибн аль-Банна», Архив истории математики Мактьютора , Университет Сент-Эндрюс
44. Гуллберг, Ян (1997). Математика: от рождения чисел . WW Norton. стр. 298. ISBN 0-393-04002-X.
45. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Абул Хасан ибн Али аль Каласади», Архив истории математики MacTutor , Университет Сент-Эндрюс
46. Boyer, CB A History of Mathematics, 2-е изд., перераб. Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7 ). "Возрождение и упадок греческой математики" стр. 178 (ср., "Главное различие между диофантовой синкопой и современной алгебраической нотацией заключается в отсутствии специальных символов для операций и отношений, а также экспоненциальной нотации".)  
47. Грант, Эдвард и Джон Э. Мердок (1987), ред., Математика и ее применение в науке и естественной философии в средние века , (Кембридж: Cambridge University Press) ISBN 0-521-32260-X . 
48. Математический журнал, том 1. Артемас Мартин, 1887. Стр. 124
49. Der Algorismusпропорционум Николауса Орема: Zum ersten Male nach der Lesart der Handschrift R.40.2. der Königlichen Gymnasial-bibliothek zu Thorn. Николь Орем . С. Голгофа и компания, 1868 г.
50. Клэгетт, Маршалл (1961) Наука механики в средние века (Мэдисон: Издательство Висконсинского университета), стр. 332–45, 382–91.
51. Поздняя ранняя современная версия : Новая система торговой арифметики: адаптированная к торговле Соединенных Штатов, в ее внутренних и внешних отношениях с формами счетов и другими письменными источниками, обычно встречающимися в торговле. Майкл Уолш. Эдмунд М. Блант (владелец), 1801.
52. Миллер, Джефф (4 июня 2006 г.). «Самые ранние примеры использования символов операции». Gulf High School . Получено 24 сентября 2006 г.
53. Арифметические книги от изобретения книгопечатания до наших дней. Август де Морган . С. 2.
54. Интегральная арифметика. Майкл Стифел , Филипп Меланчтон . Норимберге : Апуд Йохан Петреум, 1544 г.
55. История математики Энн Рун. Стр. 40
56. Мемуары Джона Нейпира из Мерчистона. Марк Нейпир
57. Рассказ о жизни, писаниях и изобретениях Джона Нейпира из Мерчистона. Дэвид Стюарт Эрскин, граф Бьюкен, Уолтер Минто
58. Каджори, Флориан (1919). История математики. Macmillan. стр. 157.
59. Синопсис Palmariorum Mathesesos. Уильям Джонс . 1706 г. (Альтернативный вариант: Synopsis Palmariorum Matheseos: или Новое введение в математику. archive.org.)
60. Когда меньше значит больше: визуализация основных неравенств. Клауди Альсина, Роджер Б. Нельс. Стр. 18.
61. Элементы геометрии. Уильям Эмерсон
62. Учение о пропорции, арифметической и геометрической. Вместе с общим методом вычисления пропорциональных величин. Уильям Эмерсон.
63. Математический корреспондент. Джордж Барон. 83
64. Disquisitions Arithmeticae (1801 г.), статья 76
65. Витулли, Мари . «Краткая история линейной алгебры и теории матриц». Кафедра математики . Университет Орегона. Архивировано из оригинала 10 сентября 2012 года . Получено 24 января 2012 года .
66. "Биография Крампа". History.mcs.st-and.ac.uk . Получено 24 июня 2014 г. .
67. Аналитическая механика: Том 1, Том 2. Жозеф Луи Лагранж . Г-жа Ве Курсье, 1811 г.
68. Собрание математических трудов Артура Кэли. Том 11. Страница 243.
69. Историческая энциклопедия естественных и математических наук, том 1. Ари Бен-Менахем. Стр. 2070.
70. Витулли, Мари . "Краткая история линейной алгебры и теории матриц". Кафедра математики. Университет Орегона. Первоначально на: darkwing.uoregon.edu/~vitulli/441.sp04/LinAlgHistory.html
71. Слова математики. Стивен Шварцман. 6.
72. Электромагнетизм: теория и приложения. А. Праманик. 38
73. История Наблы и других математических символов. homepages.math.uic.edu/~hanson.
74. "Джеймс Клерк Максвелл". IEEE Global History Network . Получено 25 марта 2013 г.
75. Максвелл, Джеймс Клерк (1865). "Динамическая теория электромагнитного поля" (PDF) . Philosophical Transactions of the Royal Society of London . 155 : 459–512. Bibcode : 1865RSPT..155..459M. doi : 10.1098/rstl.1865.0008. S2CID  186207827.(Эта статья сопровождала выступление Максвелла в Королевском обществе 8 декабря 1864 года.)
76. Книги I, II, III (1878) в Архиве Интернета ; Книга IV (1887) в Архиве Интернета
77. Риччи Курбастро, Г. (1892). «Резюме некоторых операций по системным переменным функций, связанных с квадратичной дифференциальной формой». Бюллетень математических наук . 2 (16): 167–189.
78. Фойгт, Вольдемар (1898). Фундаментальные физические свойства кристаллов в элементарном дарении. Лейпциг: Фон Файт.
79. Пуанкаре, Анри, "Анализ места", Journal de l'École Polytechnique ser 2, 1 (1895), стр. 1–123.
80. Уайтхед, Джон Б. младший (1901). «Обзор: явления переменного тока, К. П. Штейнмец» (PDF) . Bull. Amer. Math. Soc . 7 (9): 399–408. doi : 10.1090/s0002-9904-1901-00825-7 .
81. Существует много изданий. Вот два:
    • (на французском) Опубликовано в 1901 году издательством Gauthier-Villars, Париж. 230 стр. OpenLibrary OL15255022W, PDF.
    • (Итальянский) Опубликовано в 1960 году издательством Edizione Cremonese, Рим. 463 стр. Открытая библиотека OL16587658M.
82. Риччи, Грегорио ; Леви-Чивита, Туллио (март 1900 г.), «Методы дифференцированного абсолютного и leurs приложений», Mathematische Annalen , 54 (1–2), Springer: 125–201, doi : 10.1007/BF01454201, S2CID  120009332
83. Каллис, Катберт Эдмунд (март 2013). Матрицы и детерминоиды . Том 2. Cambridge University Press. ISBN 978-1-107-62083-4.
84. Может быть присвоена данная матрица: О классе матриц. (Гр. Ueber eine Klasse von Matrizen: die sich einer gegebenen Matrix zuordnen lassen.) Исай Шур
85. Введение в современную теорию уравнений. Флориан Каджори.
86. Труды Прусской академии наук (1918). Стр. 966.
87. Sitzungsberichte der Preussischen Akademie der Wissenschaften (1918) (Тр. Труды Прусской академии наук (1918)). архив.орг; См. также: Теория Калуцы–Клейна .
88. Синг Дж. Л.; Шильд А. (1949). Тензорное исчисление . Первое издание Dover Publications 1978 года. С. 6–108.
89. JA Wheeler; C. Misner; KS Thorne (1973). Гравитация . WH Freeman & Co. стр. 85–86, §3.5. ISBN 0-7167-0344-0.
90. Р. Пенроуз (2007). Дорога к реальности . Старинные книги. ISBN 978-0-679-77631-4.
91. Схоутен, Ян А. (1924). Р. Курант (ред.). Der Ricci-Kalkül – Eine Einführung in die neueren Methoden und Issuee der mehr Dimensionen Differentialgeometerie (Исчисление Риччи – Введение в новейшие методы и проблемы многомерной дифференциальной геометрии). Grundlehren der mathematischen Wissenschaften (на немецком языке). Том. 10. Берлин: Springer Verlag.
92. Роберт Б. Эш. Учебник абстрактной математики. Cambridge University Press, 1 января 1998 г.
93. Новый американский энциклопедический словарь. Под редакцией Эдварда Томаса Роу, Ле Роя Хукера, Томаса У. Хэндфорда. Стр. 34
94. Математические начала натуральной философии, том 1. Сэр Исаак Ньютон, Джон Мачин. Стр. 12.
95. В «Научном мировоззрении» (1931)
96. Математика упрощенная и привлекательная: или Законы движения объяснены. Томас Фишер. Стр. 15. (ср. Но абстракция, не основанная на Природе и ( Логической ) Истине и не согласующаяся с ними , была бы ложью , безумием . )
97. Предложение VI, О формально неразрешимых предложениях в Principia Mathematica и родственных системах I (1931)
98. Касти, Джон Л. 5 золотых правил . Нью-Йорк: MJF Books, 1996.
99. Гр. Метод математической физики
100. PAM Dirac (1927). «Квантовая теория испускания и поглощения излучения». Труды Лондонского королевского общества A. 114 ( 767): 243–265. Bibcode :1927RSPSA.114..243D. doi : 10.1098/rspa.1927.0039 .
101. Э. Ферми (1932). «Квантовая теория излучения». Reviews of Modern Physics . 4 (1): 87–132. Bibcode :1932RvMP....4...87F. doi :10.1103/RevModPhys.4.87.
102. F. Bloch ; A. Nordsieck (1937). «Заметка о поле излучения электрона». Physical Review . 52 (2): 54–59. Bibcode :1937PhRv...52...54B. doi :10.1103/PhysRev.52.54.
103. VF Weisskopf (1939). «О собственной энергии и электромагнитном поле электрона». Physical Review . 56 (1): 72–85. Bibcode : 1939PhRv...56...72W. doi : 10.1103/PhysRev.56.72.
104. Р. Оппенгеймер (1930). «Заметка о теории взаимодействия поля и материи». Physical Review . 35 (5): 461–477. Bibcode : 1930PhRv...35..461O. doi : 10.1103/PhysRev.35.461.
105. Ван дер Варден Б.Л. (1929). «Спиноранализ». Нахр. Гес. Висс. Геттинген Матем.-Физ . 1929 : 100–109.
106. Веблен О. (1933). «Геометрия двухкомпонентных спиноров». Proc. Natl. Acad. Sci. USA . 19 (4): 462–474. Bibcode :1933PNAS...19..462V. doi : 10.1073/pnas.19.4.462 . PMC 1086023 . PMID  16577541. 
107. Дирак, П. А. М. (1939). «Новая нотация для квантовой механики». Математические труды Кембриджского философского общества . 35 (3): 416–418. Bibcode :1939PCPS...35..416D. doi :10.1017/S0305004100021162. S2CID  121466183.
108. Грассман Х. (1862). Теория расширений . История источников математики. Американское математическое общество, Лондонское математическое общество, 2000 перевод Ллойда К. Канненберга.
109. Вайнберг, Стивен (1964), Квантовая теория полей, Том 2, Cambridge University Press, 1995, стр. 358, ISBN 0-521-55001-7
110. Де Феличе, Ф.; Кларк, CJS (1990), Относительность на искривленных многообразиях , стр. 133
111. "Квантовые инварианты узлов и 3-многообразий" В.Г. Тураев (1994), стр. 71
112. Писански, Томаж ; Серватиус, Бригитта (2013), "2.3.2 Кубические графы и нотация LCF", Конфигурации с графической точки зрения, Springer, стр. 32, ISBN 978-0-8176-8364-1
113. Фрухт, Р. (1976), «Каноническое представление трехвалентных гамильтоновых графов», Журнал теории графов , 1 (1): 45–60, doi :10.1002/jgt.3190010111
114. Фрели 2002:89; Хангерфорд 1997: 230
115. Ден, Эдгар. Алгебраические уравнения, Дувр. 1930:19
116. "IBM 601 Multiplying Punch". Columbia.edu . Получено 24 июня 2014 г.
117. "Interconnected Punched Card Equipment". Columbia.edu. 24 октября 1935 г. Получено 24 июня 2014 г.
118. Макдоннелл, Юджин , ред. (1981), A Source Book in APL, Introduction, APL Press , получено 19 апреля 2016 г.

Дальнейшее чтение

Общий

• Краткий обзор истории математики. Уолтер Уильям Рауз Болл .
• Учебник истории математики. Уолтер Уильям Рауз Болл.
• История элементарной математики: с советами по методам обучения. Флориан Каджори.
• История элементарной математики. Флориан Каджори.
• История математики. Флориан Каджори.
• Краткая история греческой математики. Джеймс Гоу .
• О развитии математической мысли в девятнадцатом веке. Джон Теодор Мерц .
• Новый математический и философский словарь. Питер Барлоу.
• Историческое введение в математическую литературу. Джордж Абрам Миллер
• Краткая история математики. Карл Финк, Вустер Вудрафф Беман, Дэвид Юджин Смит
• История современной математики. Дэвид Юджин Смит.
• История современной математики. Дэвид Юджин Смит, Мэнсфилд Мерриман .

Другой

• Principia Mathematica, том 1 и том 2. Альфред Норт Уайтхед, Бертран Рассел.
• Математические начала натуральной философии, том 1, выпуск 1. Авторы: сэр Исаак Ньютон, Эндрю Мотт, Уильям Дэвис, Джон Мачин, Уильям Эмерсон.
• Общие исследования криволинейных поверхностей 1827 и 1825 годов. Карл Фридрих Гаус.

Внешние ссылки

• Математическая нотация: прошлое и будущее
• История математической нотации
• Ранние примеры использования математической нотации
• Подсчет пальцев. files.chem.vt.edu.
• Некоторые распространённые математические символы и сокращения (с историей). Исайя Ланкхэм, Бруно Нахтергале, Энн Шиллинг.